Как найти середину интервала в экселе
1. Определить выборочные оценки числовых характеристик случайной величины.
Для нахождения выборочных оценок скопируем данные задачи в один столбец таблицы MS Excel . Выделите полученный столбец и на панели инструментов щелкните на кнопку Сортировка и фильтр . В появившемся окошке нажмите сортировку от А до Я. В выделенном столбце значения упорядочатся от наименьшего к наибольшему.
Проанализируем данные с помощью описательной статистики. Для этого на вкладке Данные в группе Анализ щелкните на кнопку Анализ данных . Откроется диалоговое окно Анализ данных.
Выберите инструмент Описательная статистика и щелкните на кнопке Ок . Откроется диалоговое окно Описательная статистика.
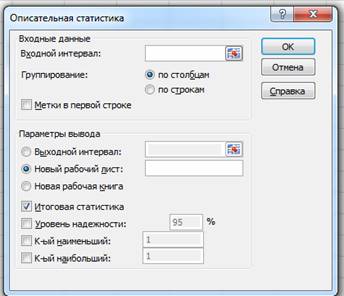
2. Построить вариационный ряд, или ряд распределений и гистограмму для него.
Как видно в итоговой статистике, все возможные значения данного распределения укладываются в интервал 3σ.
Действительно, x =69,43; 3σ=27,3; ( x -3σ; x +3σ) = (41,13; 96,73)
Размах выборки 43,6. Разбиваем данный ряд на 7 интервалов длины 43,6: 7≈6,2.
Составим таблицу ряда распределений:
Чтобы создать диаграмму, выберите нужные данные таблицы (границы интервала и число наблюдений в интервале) и на вкладке Вставка в группе Диаграммы щелкните на типе диаграммы. Появится список доступных подтипов диаграмм. При щелчке на подтипе диаграммы будет создана диаграмма с макетом и цветовой схемой по умолчанию, определенными в теме оформления книги.
3. Определить теоретическую функцию распределения, её параметры. Выполнить сравнительный графический анализ формы эмпирического и теоретического распределений.
Для построения графика теоретической функции распределения построим вспомогательную таблицу:
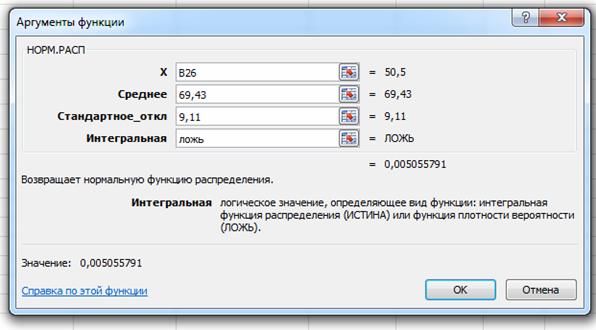
В открывшемся окне в поле X указываем на ячейку со значением середины интервала, в поле Среднее указываем среднее значение, полученное в первом пункте работы с помощью описательной статистики, в поле Стандартное_откл – стандартное отклонение, найденное также с помощью описательной статистики. В поле Интегральная – ЛОЖЬ, так как ищем функцию плотности вероятности и нажимаем ОК.
Теоретическая вероятность вычисляется по формуле:
В таблице 2 выделяем последний столбец и строим график теоретической вероятности. Для этого на вкладке Вставка в группе График щелкните на типе графика. Появится список доступных подтипов графиков. При щелчке на подтипе графика будет создан график с макетом и цветовой схемой по умолчанию, определенными в теме оформления книги.
Изначально на горизонтальной оси обозначены номера интервалов. Правой кнопкой мыши щелкаем на эту ось и нажимаем на Выбрать данные . Меняем подпись горизонтальной оси, указывая первый столбец таблицы 2. Нажимая на график правой кнопкой мыши можно поменять цвет графика.
А теперь выполним сравнительный графический анализ формы эмпирического и теоретического распределений построением графика теоретической вероятности на гистограмме частот.
Для этого построим гистограмму частостей на интервалах. Щелкнем правой кнопкой мыши в поле гистограммы и нажмем на кнопку Выбрать данные . В открывшемся окне в левом столбце Элементы легенды нажмем кнопку Добавить . Откроется окно Изменение ряда . Имя ряда: укажем на ячейку Теоретическая вероятность, значения: выделим соответствующую строку. После нажатия Ок появится гистограмма теоретических вероятностей. Укажем на неё правой кнопкой мыши и выберем Изменить тип диаграммы для ряда, выбрав график. Также поменяем цвет нового графика.
4.Проверка согласованности теоретического и эмпирического распределений.
Схема применения критерия Χ 2 для проверки гипотезы H0 о соответствии эмпирического ряда нормальному закону распределения, сводится к следующему.
1) Определяется мера расхождения эмпирических и теоретических частот Χ 2 по формуле .
Для этого в свободной ячейке нажмем на вкладке Формулы выберем Статистические и, среди них ХИ2.ТЕСТ. Откроется следующее окно:
При статистической обработке результатов исследований самого разного рода полученные значения часто группируются в последовательность интервалов. Для расчета обобщающих характеристик таких последовательностей иногда приходится вычислять середину интервала - «центральную варианту». Методы ее расчета достаточно просты, но имеют некоторые особенности, вытекающие как из используемой для измерения шкалы, так и из характера группировки (открытые или закрытые интервалы).

- Как найти середину интервала
- Как построить интервальный вариационный ряд
- Как решать методом интервала
Если интервал является участком непрерывной числовой последовательности, то для нахождения ее середины используйте обычные математические методы вычисления среднеарифметического значения. Минимальное значение интервала (его начало) сложите с максимальным (окончанием) и разделите результат пополам - это один из способов вычисления среднеарифметического значения. Например, это правило применимо, когда речь идет о возрастных интервалах. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, так как (21+33)/2=27.
Иногда бывает удобнее использовать другой метод вычисления среднеарифметического значения между верхней и нижней границами интервала. В этом варианте сначала определите ширину диапазона - отнимите от максимального значения минимальное. Затем поделите полученную величину пополам и прибавьте результат к минимальному значению диапазона. Например, если нижняя граница соответствует значению 47,15, а верхняя - 79,13, то ширина диапазона составит 79,13-47,15=31,98. Тогда серединой интервала будет 63,14, так как 47,15+(31,98/2) = 47,15+15,99 = 63,14.
Если интервал не является участком обычной числовой последовательности, то вычисляйте его середину в соответствии с цикличностью и размерностью используемой измерительной шкалы. Например, если речь идет об историческом периоде, то серединой интервала будет являться определенная календарная дата. Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.
Кроме обычных (закрытых) интервалов статистические методы исследований могут оперировать и «открытыми». У таких диапазонов одна из границ не определена. Например, открытый интервал может быть задан формулировкой «от 50 лет и старше». Середина в этом случае определяется методом аналогий - если все остальные диапазоны рассматриваемой последовательности имеют одинаковую ширину, то предполагается, что и этот открытый интервал имеет такую же размерность. В противном случае вам надо определить динамику изменения ширины интервалов, предшествующих открытому, и вывести его условную ширину, исходя из полученной тенденции изменения.
Количественные данные следует определить как «Числовые».
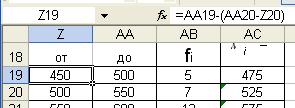
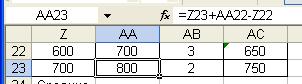
Формула вычисления левой границы первого интервала вводится в ячейку Z19 : «=АА19-(АА20-Z20)» (– из ячейки АА19 вычесть разницу между содержимым ячейки АА20 и Z20).
Правая граница последнего интервала в ячейку АА23 устанавливается формулой «=Z23+АА22-Z22» (от значения в ячейке Z23 откладывается размер предшествующего интервала «АА22-Z22»).
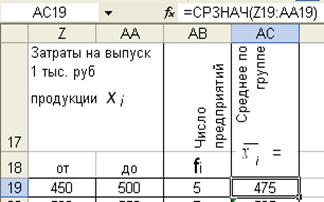
3. Рассчитывается среднее по каждой группе , как середина интервала. Для этого в ячейку первой группы (АС19) устанавливается функция СРЗНАЧ(Z19;AA19). После появления среднего значения первого интервала формула копируется в соседние ячейки. При этом автоматически смещаются координаты исходных данных в соответствии со смещением координат ячейки результата.
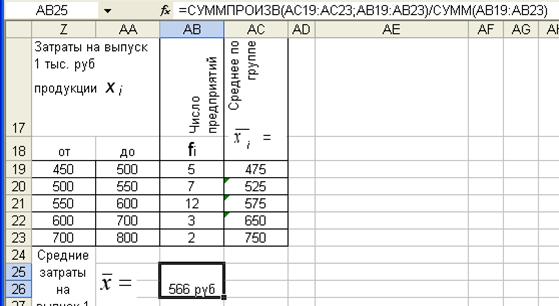
4. Рассчитывается величина средней взвешенной (в примере в ячейку АВ25)
СУММПРОИЗВ (АС19:АС23;АВ19:АВ23) реализует числитель
СУММ (АВ19:АВ23) – знаменатель;
Дисперсия. Среднее квадратическое
отклонение.
Дисперсия и среднее квадратическое отклонение (СКО) могут вычисляться по простой и взвешенной формулам.
Дисперсия, среднее квадратическое отклонение
по простой форме.
Для расчетов дисперсии по простой форме в Excel используется функция:
ДИСПР (диапазон данных).
СКО определяется как квадратный корень дисперсии, реализуемый оператором возведения в степень «^».
Рассмотрим методику расчета на примере расчета дисперсии и СКО зарплаты подразделения:

1. Исходные значения признака хi надо записать в массив ячеек расположенных в столбце или строке (в примере в строке (AF42:AQ42)).
Количественные данные следует определить как «Числовые».
2. В ячейку результата дисперсии (например «AF44») установить функцию ДИСПР(AF42:AQ42)
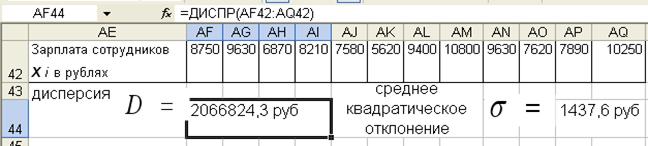
1. В ячейку результата СКО (например «AР44») установить функцию (ДИСПР(AF42:AQ42))^0,5.
Дисперсия, среднее квадратическое
отклонение по взвешенной форме.
Для расчетов дисперсии по взвешенной форме в Excel используется функция:
СУММ (диапазон данных) и
СУММПРОИЗВ (диапазоны перемножаемых данных),
СКО определяется как квадратный корень дисперсии, реализуемый оператором возведения в степень «^».
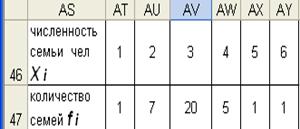
Рассмотрим методику расчета на примере расчета дисперсии и СКО размера семьи группы
1. Исходные значения признака хi и частоту fi надо записать в массивы ячеек расположенных в столбце или строке (в примере в строках (АТ46:AY46) и (АТ47:AY47).
Количественные данные следует определить как «Числовые».
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 266
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 171
- БГТУ 602
- БГУ 153
- БГУИР 391
- БелГУТ 4908
- БГЭУ 962
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 119
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им. Даля 166
- ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 497
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 130
- ИжГТУ 143
- КемГППК 171
- КемГУ 507
- КГМТУ 269
- КировАТ 147
- КГКСЭП 407
- КГТА им. Дегтярева 174
- КнАГТУ 2909
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 107
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 367
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 330
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 636
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 454
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 212
- НУК им. Макарова 542
- НВ 778
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1992
- НГУЭУ 499
- НИИ 201
- ОмГТУ 301
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 119
- РАНХиГС 186
- РОАТ МИИТ 608
- РТА 243
- РГГМУ 117
- РГПУ им. Герцена 123
- РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 122
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 130
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1598
- СПбГТИ (ТУ) 292
- СПбГТУРП 235
- СПбГУ 577
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 193
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им. Гагарина 113
- СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2423
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им. Каразина 305
- ХНУРЭ 324
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 306
Полный список ВУЗов
Чтобы распечатать файл, скачайте его (в формате Word).
Задача по статистике №1. Найти параметры интервального ряда распределения по данным таблицы, а именно: моду, медиану, среднюю арифметическую величину, среднюю взвешенную величину, коэффициент вариации, среднее квадратическое отклонение.
Группы компаний по основным производственным фондам, млн. руб. (х)
Число компаний (fi)
Середина интервала (Xi) = (начало интервала+конец интервала)/2
Мы сразу добавили столбец «середина интервала». Для первой группы компаний рассчитали следующим образом: (10+25)/2=17,5 млн. руб. Для 2-5 групп расчеты произведены аналогично.
Теперь рассчитаем среднюю арифметическую величину.
средняя арифметическая = = (17,5+29+37,5+45,5+55,5)/5=37 млн. руб.
Далее рассчитаем среднюю взвешенную величину.
средняя взвешенная = = (17,5*2+29*8+37,5*14+45,5*9+55,5*3)/36=38 млн. руб.
Значение средневзвешенной величины можно считать более корректным, чем значение средней арифметической величины, поэтому далее в расчетах будем использовать среднюю взвешенную.
Теперь добавим в таблицу столбцы, данные которых нам понадобятся для расчета дисперсии.
Число компаний (f)
Середина интервала (Xi) = (начало интервала+конец интервала)/2
При статистической обработке итогов изысканий самого различного рода полученные значения зачастую группируются в последовательность промежутков. Для расчета обобщающих колляций таких последовательностей изредка доводится вычислять середину интервала – «центральную варианту». Способы ее расчета довольно примитивны, но имеют некоторые особенности, вытекающие как из применяемой для измерения шкалы, так и из нрава группировки (открытые либо закрытые промежутки).

Инструкция
1. Если промежуток является участком постоянной числовой последовательности, то для нахождения ее середины используйте обыкновенные математические способы вычисления среднеарифметического значения. Минимальное значение интервала (его предисловие) сложите с максимальным (окончанием) и поделите итог напополам – это один из методов вычисления среднеарифметического значения. Скажем, это правило применимо, когда речь идет о возрастных интервала х. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, потому что (21+33)/2=27.
2. Изредка бывает комфортнее применять иной способ вычисления среднеарифметического значения между верхней и нижней границами интервала . В этом варианте вначале определите ширину диапазона – отнимите от максимального значения минимальное. После этого поделите полученную величину напополам и прибавьте итог к минимальному значению диапазона. Скажем, если нижняя граница соответствует значению 47,15, а верхняя – 79,13, то ширина диапазона составит 79,13-47,15=31,98. Тогда серединой интервала будет 63,14, потому что 47,15+(31,98/2) = 47,15+15,99 = 63,14.
3. Если промежуток не является участком обыкновенной числовой последовательности, то вычисляйте его середину в соответствии с повторяемостью и размерностью применяемой измерительной шкалы. Скажем, если речь идет об историческом периоде, то серединой интервала будет являться определенная календарная дата. Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.
4. Помимо обыкновенных (закрытых) промежутков статистические способы изысканий могут оперировать и «открытыми». У таких диапазонов одна из границ не определена. Скажем, открытый промежуток может быть задан формулировкой «от 50 лет и старше». Середина в этом случае определяется способом аналогий – если все остальные диапазоны рассматриваемой последовательности имеют идентичную ширину, то предполагается, что и данный открытый промежуток имеет такую же размерность. В отвратном случае вам нужно определить динамику метаморфозы ширины промежутков, предшествующих открытому, и вывести его условную ширину, исходя из полученной склонности метаморфозы.
Изредка в повседневной деятельности может появиться надобность обнаружить середину отрезка прямой линии. Скажем, если предстоит сделать выкройку, эскиз изделия либо легко распилить на две равные части деревянный брусок. На поддержка приходит геометрия и немножко житейской смекалки.
Вам понадобится
Инструкция
1. Воспользуйтесь обыкновенными инструментами, предуготовленными для измерения длины. Это самый легкой метод разыскать середину отрезка. Измерьте линейкой либо рулеткой длину отрезка, поделите полученное значение напополам и отмерьте от одного из концов отрезка полученный итог. Вы получите точку, соответствующую середине отрезка.
2. Существует больше точный метод нахождения середины отрезка, вестимый из курса школьной геометрии. Для этого возьмите циркуль и линейку, причем линейку может заменить всякий предмет подходящей длины с ровной стороной.
3. Установите расстояние между ножками циркуля так, дабы оно было равным длине отрезка либо же огромным, чем половина отрезка. После этого поставьте иглу циркуля в один из концов отрезка и проведите полуокружность так, дабы она пересекала отрезок. Переставьте иглу в иной конец отрезка и, не меняя размах ножек циркуля, проведите вторую полуокружность верно таким же образом.
4. Вы получили две точки пересечения полуокружностей по обе стороны от отрезка, середину которого мы хотим обнаружить. Объедините эти две точки при помощи линейки либо ровного бруска. Соединительная линия пройдет в точности посередине отрезка.
5. Если под рукой не оказалось циркуля либо длина отрезка значительно превышает возможный размах его ножек, дозволено воспользоваться простым приспособлением из подручных средств. Изготовить его дозволено из обыкновенной булавки, нитки и карандаша. Привяжите концы нитки к булавке и карандашу, при этом длина нитки должна немножко превышать длину отрезка. Таким импровизированным заменителем циркуля остается проделать шаги, описанные выше.
Видео по теме
Полезный совет
Довольно верно обнаружить середину доски либо бруска вы можете, использовав обыкновенную нитку либо шнур. Для этого отрежьте нить так, дабы она соответствовала длине доски либо бруска. Остается сложить нить верно напополам и разрезать на две равные части. Приложите один конец полученной мерки к концу измеряемого предмета, а 2-й конец будет соответствовать его середине.
Интервалы используются в математике по разным причинам. Интервал - это определенный сегмент набора данных. Например, интервал может быть от 4 до 8. Интервалы используются в статистике и в исчислении при получении интегралов. Интервалы также используются при попытке найти среднее из частотных таблиц. Средняя точка каждого интервала необходима для завершения этого процесса и определения среднего значения.
Найти верхний и нижний предел интервала. Например, интервал от 4 до 8 будет иметь 4 в качестве нижнего предела и 8 в качестве верхнего предела.
Суммируйте верхний и нижний предел. В примере 4 + 8 = 12.
Разделите сумму верхнего и нижнего пределов на 2. Результат - средняя точка интервала. В этом примере 12, деленное на 2, дает 6 как среднюю точку между 4 и 8.
Как найти абсолютное значение числа в математике

Распространенной задачей в математике является вычисление того, что называется абсолютным значением данного числа. Как правило, мы используем вертикальные полосы вокруг числа, чтобы отметить это, как видно на рисунке. Мы будем читать левую часть уравнения как абсолютное значение -4. Компьютеры и калькуляторы часто используют формат .
Как рассчитать размер выборки из доверительного интервала

Когда исследователи проводят опросы общественного мнения, они рассчитывают необходимый размер выборки на основе того, насколько точными они хотят, чтобы их оценки были. Размер выборки определяется уровнем достоверности, ожидаемой пропорцией и доверительным интервалом, необходимым для обследования. Доверительный интервал представляет запас .
Как найти середину координат

Средняя точка двух координат - это точка, которая находится точно посередине между двумя точками, или среднее значение двух точек. Вместо того, чтобы пытаться визуально определить полпути крутой линии, проведенной на координатной плоскости, вы можете использовать формулу средней точки. Формула средней точки - [(x1 + x2) / 2, (y1 + y2) / 2] - .
Читайте также:


