Как экран делится на равные части если пикселей нечетное количество
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 128×128 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Один пиксель кодируется 8 битами памяти, так как 2 8 = 256.
Тогда объем памяти, занимаемый изображением 2 14 * 8 = 2 17 бит = 2 14 байт = 2 4 Кбайт = 16 Кбайт.
Откуда там 8? Может быть 2 в 8 степени? И ответ тогда 512 Кб
На каждый пиксель 8 бит, всего 2 14 пикселей. Сколько бит на все пиксели? Правильно: .
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 128×128 пикселей при условии, что в изображении могут использоваться 128 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Один пиксель кодируется 7 битами памяти.
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 512x512 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Для того, чтобы закодировать один пиксель, то есть 256 цветов, требуется
Всего пикселей , то есть и памяти понадобится
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 1024x1024 пикселей при условии, что в изображении могут использоваться 16 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Для того, чтобы закодировать один пиксель, то есть 16 цветов, требуется
Всего пикселей , то есть и памяти понадобится
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 320×640 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Заметим, что 256 = 2 8 , то есть для хранения цвета одного пиксела изображения нужно использовать Значит, для хранения изображения размером 320×640 пикселей нужно использовать:
Постараюсь подробно "на пальцах" рассказать, как изображение записывается в память машины.
Итак. Главный тезис: для того, чтобы послать нашему другу мемчик или сохранить демотиватор себе на телефон, требуется изобразить его в "ноликах и единичках".
О памяти машины
Потому что память машины устроена именно так: она содержит сплошняком ячейки, в которых может быть только "0" или "1". Конечно, там не цифры записаны. Они только называются "логический ноль" или "логическая единица". На самом деле, всё зависит от технологии, по которой изготовлена память машины. Например, кучу лет назад (даже "олды" не все припомнят) существовали перфокарты. Такие картонные карточки с цифрами. У них ещё уголок один был срезан:
В качестве логических нулей и единиц использовались дырочки. 864 дырочки или "недырочки". Технология, вообще-то, не очень. Если оператор ошибался в одной дырочке, то карту приходилось менять полностью. Ну, или заклеивать/прорезать лезвием. В современных машинах, конечно, и метод другой, и количество немного больше (в Вкипедии написано, что "кинчик" на 1 гигабайт, в прямом смысле, весил бы 22 тонны, если бы его на перфокартах пробивали).
В разных ситуациях словом бит называют:
- одни значок (дырочка-недырочка, ноль-один)
- одно место, на котором может быть записан либо ноль, либо один
- единицу измерения количества информации
Очень важная деталь. Биты (2) сгруппированы в сегменты по 8 штук. Такие сегменты называются байты . Аналогично битам, у слова "байт" есть несколько значений. Важно то, что машина не может прочитать один бит. За раз ей нужно прочитать целый байт, а только потом из него выделить бит. То же с записью - за раз можно записать только один целый байт, но не бит. Если нам надо поменять один бит, мы должны считать весь байт, заменить там бит с помощью логических операций, перезаписать байт обратно.
Про изображения
Существует масса способов записать картинку только ноликами и единичками. В школе проходят растровый и векторный. К векторному, возможно, я обращусь ещё, а вот про растровый расскажу подробнее. Суть проста: изображение разбивается на одинаковые клеточки. Эти клеточки называются "пиксели" или "пикселы". Кто как привык. Каждый пиксель имеет один единственный цвет. Получается мозаика.

Пространство изображений огромно, невероятно огромно, но при этом очень мало. Задумайтесь об этом на минуту. Из сетки размером всего 8 на 8 пикселей можно создать 18 446 744 073 709 551 616 различных чёрно-белых изображений. Однако из этих 18 квинтиллионов изображений очень немногие покажутся осмысленными человеческому взгляду. Большинство изображений, по сути, выглядит как QR-коды. Те, которые покажутся человеку осмысленными, принадлежат к тому множеству, которое я называю естественными изображениями. Они представляют крошечную долю пространства изображений 8 на 8. Если мы рассмотрим мегапиксельные изображения, то доля естественных изображений становится ещё меньше, почти ничтожной, однако содержит любое изображение, которое можно придумать. Так чем же эти естественные изображения так уникальны? И можем ли мы использовать эту фундаментальную разницу в собственных интересах?
Спектральное пространство

Слева: случайное изображение. Справа: классическое тестовое изображение женщины с тёмными волосами. Оба изображения принадлежат к пространству изображений 512 на 512
Чтобы понять фундаментальную разницу между этими изображениями, нам нужно покинуть пространство пикселей и войти в мир частотного диапазона. С точки зрения математики, преобразование Фурье — это линейное сопоставление пиксельного описания изображения с описанием в виде суммы синусов и косинусов, колеблющихся в двух измерениях. Вместо задания изображения значениями, принимаемыми каждым пикселем, мы задаём его по амплитудам каждого из составляющих его двухмерных синусов и косинусов.
Описание этих двух изображений в пространстве Фурье представлено ниже. Для отображения величины коэффициента Фурье использована логарифмическая шкала. Разница между двумя изображениями теперь очевидна. Одно имеет гораздо больше ненулевых коэффициентов Фурье, чем другое. На языке математики говорится, что естественное изображение является разреженным по базису Фурье. Именно разреженность отличает естественные изображения от случайных. Давайте же используем эту разницу с пользой для себя!
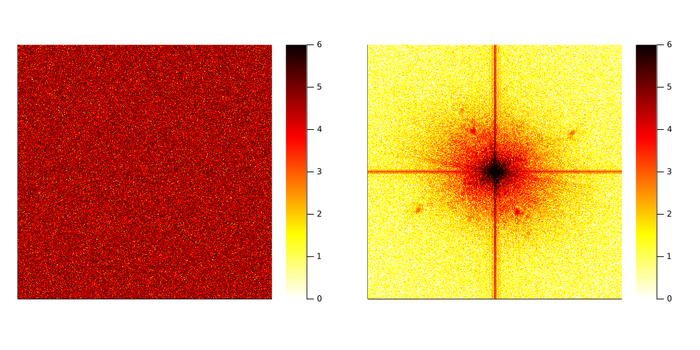
Амплитуда преобразований Фурье обоих изображений. Использована логарифмическая шкала
Воссоздание изображений по нескольким пикселям, задача с высокой степенью неопределённости

Записано всего 10% пикселей
Рассмотрим следующую ситуацию: по какой-то неизвестной причине большинство фотодатчиков камеры оказалось неисправным. Скопировав на компьютер только что сделанную фотографию своей жены (или матери, или друга), вы обнаружили, что изображение получилось таким, как показано выше. Можно ли как-то восстановить изображение?
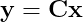
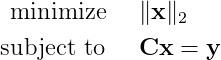
решение которой задаётся так:
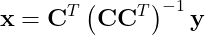
Используем разреженность в спектральном пространстве
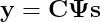
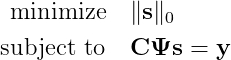
К сожалению, это задача комбинаторики, очень быстро становящаяся нерешаемой. Чтобы найти её решение, потребуется проверить все возможные сочетания. К счастью в своей революционной работе 2006 года Канде et al. [1, 2] показал, что при условии разумных допущений решение изложенной выше задачи можно получить (с высокой вероятностью) при помощи решения более простой задачи:
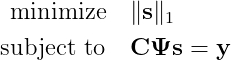
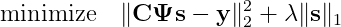

Слева: оригинал изображения. Справа: изображение, воссозданное при помощи compressive sensing на основании данных всего 10% пикселей
Даже несмотря на то, что исправно работало всего 10% фотодатчиков камеры, формулировка этой задачи восстановления изображения в рамках Compressed Sensing позволяет нам воссоздать достаточно точное приближение к тому, каким было исходное изображение! Очевидно, что оно всё равно неидеально, однако учитывая обширность пространства изображений и бесконечное количество решений нашей задачи, нужно признать, что результат довольно хорош!
Методика Compressed Sensing совершила революцию в сфере обработки сигналов. Если мы заранее знаем, что сигнал, с которым работаем, разрежен по указанному базису, то compressed sensing позволяет восстановить его по гораздо меньшему количеству сэмплов, чем предполагается по теореме выборки Найквиста-Шеннона. Кроме того, она позволяет значительно сжимать данные непосредственно на этапе получения, уменьшая таким образом необходимый объём хранилища данных. Также Compressed Sensing привела к возникновению неожиданных новых технологий, например, однопиксельной камеры, разработанной Университетом Райса, или новых техник обработки для создания визуализаций МРТ в медицине. Я не сомневаюсь, что в ближайшие несколько лет мы станем свидетелями множества новых способов применения этой методики.
Compressed sensing — это гораздо более глубокая область математики, чем можно судить по этому ознакомительному посту. Существует ещё множество не рассмотренных нами вопросов, например:
- Каково наименьшее количество необходимых измерений?
- Могут ли некоторые измерения быть информативнее других?
- Существуют ли другие нормы, лучше подходящие для изображений?
Для ответа на эти вопросы потребуется гораздо больше математики, чем можно представить в посте. Если вы хотите знать больше, то крайне рекомендую изучить оригиналы статей, ссылки на которые я указал в конце. Также стоит изучить потрясающий веб-сайт Numerical Tours Габриеля Пейре или последнюю книгу Брантона и Кутца [3], а также соответствующий канал на YouTube (здесь и здесь).
Ссылки на научные работы
[3] Brunton S. L. and Kutz J. N. Data-driven science and engineering: machine learning, dynamical systems, and control. Cambridge University Press, 2019.
Что такое разрешение экрана?
Изображение на экране вашего компьютера состоит из тысяч или миллионов пикселей. Экран создает изображение, которое вы видите, изменяя цвета этих крошечных квадратных элементов.
Разрешение экрана говорит вам, сколько пикселей ваш экран может отображать по горизонтали и вертикали. Это написано в формуле 1920 х 1080. В этом примере экран может отображать 1920 пикселей по горизонтали и 1080 по вертикали.
Разные размеры экрана, одинаковое разрешение
Теперь все становится немного сложнее. Экраны разных размеров могут иметь одинаковое разрешение экрана. С годами цена на мониторы резко упала, поэтому может возникнуть соблазн купить самый большой экран, который вы можете себе позволить.
Но размер не единственное соображение. У вас может быть ноутбук с 15-дюймовым экраном и разрешением 1366 x 786. У вас также может быть 21-дюймовый монитор на столе с тем же разрешением 1366 x 786.
В этом примере, хотя монитор на вашем столе больше, на самом деле вы не сможете разместить на нем ничего лишнего. Общее количество пикселей одинаково.
Это означает, что выбор правильного экрана означает, что вы должны принять во внимание как размер экрана, так и его разрешение.
Что означает более высокое разрешение?
Если вы сравниваете два экрана одинакового размера, но с разным разрешением, то экран с более высоким разрешением (то есть с большим количеством пикселей) сможет показать вам больше информации, поэтому вам не придется много раз прокручивать экран.
Поскольку этот экран имеет больше пикселей, изображение будет более четким. Однако более высокое разрешение также означает, что элементы на экране, такие как значки и текст, будут выглядеть меньше.
Сейчас в продаже есть множество вариантов мониторов с самыми разными разрешениями экрана, чем когда-либо. Теперь можно купить мониторы высокой четкости (1 366 x 768), полной высокой четкости (1 920 x 1 080), широкоэкранного графического массива со сверхвысоким разрешением (1 920 x 1 200) и даже мониторы сверхвысокой четкости (3 840 x 2160), также известные как 4K.
Дело не только в разрешении экрана
Итак, есть несколько практических правил, которые помогут вам выбрать правильное разрешение:
| Название | Разрешение матрицы и соотношение сторон | Количество пикселей |
|---|---|---|
| QVGA | 320 x 240 (4:3) | 76,8 кпикс |
| SIF(MPEG1 SIF) | 352 x 240 (22:15) | 84,48 кпикс |
| CIF(MPEG1 VideoCD) | 352 x 288 (11:9) | 101,37 кпикс |
| WQVGA | 400 x 240 (5:3) | 96 кпикс |
| [MPEG2 SV-CD] | 480 x 576 (5:6 – 12:10) | 276,48 кпикс |
| HVGA | 640 x 240 (8:3) или 320 x 480 (2:3 – 15:10) | 153,6 кпикс |
| nHD | 640 x 360 (16:9) | 230,4 кпикс |
| VGA | 640 x 480 (4:3 – 12:9) | 307,2 кпикс |
| WVGA | 800 x 480 (5:3) | 384 кпикс |
| SVGA | 800 x 600 (4:3) | 480 кпикс |
| FWVGA | 854 x 480 (427:240) | 409,92 кпикс |
| WSVGA | 1024 x 600 (128:75 – 15:9) | 614,4 кпикс |
| XGA | 1024 x 768 (4:3) | 786,432 кпикс |
| XGA+ | 1152 x 864 (4:3) | 995,3 кпикс |
| WXVGA | 1200 x 600 (2:1) | 720 кпикс |
| WXGA | 1280 x 768 (5:3) | 983,04 кпикс |
| SXGA | 1280 x 1024 (5:4) | 1,31 Мпикс |
| WXGA+ | 1440 x 900 (8:5 – 16:10) | 1,296 Мпикс |
| SXGA+ | 1400 x 1050 (4:3) | 1,47 Мпикс |
| XJXGA | 1536 x 960 (8:5 – 16:10) | 1,475 Мпикс |
| WSXGA (x) | 1536 x 1024 (3:2) | 1,57 Мпикс |
| WXGA++ | 1600 x 900 (16:9) | 1,44 Мпикс |
| WSXGA | 1600 x 1024 (25:16) | 1,64 Мпикс |
| UXGA | 1600 x 1200 (4:3) | 1,92 Мпикс |
| WSXGA+ | 1680 x 1050 (8:5) | 1,76 Мпикс |
| Full HD | 1920 x 1080 (16:9) | 2,07 Мпикс |
| Full HD+ | 2340 x 1080 (19,5:9) | 2,3 Мпикс |
| WUXGA | 1920 x 1200 (8:5 – 16:10) | 2,3 Мпикс |
| QWXGA | 2048 x 1152 (16:9) | 2,36 Мпикс |
| QXGA | 2048 x 1536 (4:3) | 3,15 Мпикс |
| WQXGA | 2560 x 1440 (16:9) | 3,68 Мпикс |
| WQXGA | 2560 x 1600 (8:5 – 16:10) | 5,24 Мпикс |
| WQSXGA | 3200 x 2048 (25:16) | 6,55 Мпикс |
| QUXGA | 3200 x 2400 (4:3) | 7,68 Мпикс |
| WQUXGA | 3840 x 2400 (8:5 – 16:10) | 9,2 Мпикс |
| 4K (Quad HD) | 4096 x 2160 (256:135) | 8,8 Мпикс |
| HSXGA | 5120 x 4096 (5:4) | 20,97 Мпикс |
| WHSXGA | 6400 x 4096 (25:16) | 26,2 Мпикс |
| HUXGA | 6400 x 4800 (4:3) | 30,72 Мпикс |
| Super Hi-Vision | 7680 x 4320 (16:9) | 33,17 Мпикс |
| WHUXGA | 7680 x 4800 (8:5, 16:10) | 36,86 Мпикс |
Развертка экрана: что это такое?
Возможно, вы видели разрешение экрана, описанное как что-то вроде 720p, 1080i или 1080p. Что это обозначает? Начнем с того, что буквы рассказывают о том, как картинка «рисуется» на мониторе. «Р» означает прогрессивный, а «I» означает чересстрочный.
Чересстрочная развертка является пережитком телевизионных и ранних ЭЛТ-мониторов. На экране монитора или телевизора линии пикселей расположены горизонтально. Линии было относительно легко увидеть, если вы приблизились к старому монитору или телевизору, но в настоящее время пиксели на экране настолько малы, что их трудно увидеть даже при увеличении.
Электроника монитора «рисует» каждый экран построчно и слишком быстро, чтобы глаз мог видеть её. Чересстрочный дисплей сначала рисует все нечетные строки, а затем все четные строки. Поскольку экран раскрашивается чередующимися линиями, мерцание всегда было проблемой при чересстрочном сканировании.
Производители пытались преодолеть эту проблему различными способами. Наиболее распространенным способом является увеличение количества раз, когда весь экран отображается в секунду, что называется частотой обновления.
Самая распространенная частота обновления составляла 60 раз в секунду, что приемлемо для большинства людей, но ее можно увеличить лишь немного, чтобы избавиться от мерцания, которое некоторые люди все еще ощущают.
Вот как изображение отображается на прогрессивном дисплее по сравнению с чересстрочным
В последних версиях Windows частота кадров составляет 60 Гц или 60 циклов в секунду, а светодиодные экраны не мерцают вообще. Более того, система перешла с чересстрочной развертки на прогрессивную, потому что новые цифровые дисплеи стали намного быстрее. При прогрессивном сканировании линии отображаются на экране последовательно, а не сначала нечетными, а затем четными.
Читайте также:


