Цикл карно описание каждого участка
Мы, как простые обыватели, редко задумываемся над тем, как работают тепловые двигателя, и уж тем более - не пытаемся вникнуть в суть происходящего внутри этих самых двигателей с точки зрения термодинамики. Среднестатистические познания механиков и техников ограничиваются тем, что, вроде как, что-то там внутри сгорает, и благодаря этому начинают шевелиться поршни (в простонародье - "поршня") , вращая другие детали и, как говорится, "процесс пошел".
Но, как всегда, среди людского роду-племени находятся наиболее дотошные представители, которым просто необходимо знать, как на самом деле все происходит и от чего все зависит. Наверное, на этих "дотошных" и "вездесущих", как на ветках деревьев и произрастают плоды, вскармливающие науку.
Итак, давайте попробуем разобраться - как же работает тепловой двигатель, и от чего зависит его эффективность?
Немного теории.
Тепловым двигателем называют такую машину, которая способна преобразовывать энергию тепла в энергию механического движения. Т. е. внутри этих механизмов, представляющих собой систему, что-то начинает вращаться, перемещаться и кувыркаться, если каким-либо образом изменить температуру внутри этой самой системы (как правило, тепло подводят к рабочему телу, которое чаще всего по ряду "уважительных" причин является газом) .
Ну и еще немного - все двигатели подразделяют, по большому счету, на двигатели внутреннего сгорания и двигатели внешнего сгорания.
У первых подвод тепла к элементу системы совершается внутри двигателя, у вторых - где-то снаружи. Забегая вперед, приведем пример: к двигателям внешнего сгорания относят, в частности, паровые двигатели, в которых тепло к рабочему телу (льду, воде или пару или какой-либо жидкости) подводится вне двигателя, путем сжигания какого-нибудь топлива (угля, мазута, дров и т. п.) в отдельно расположенной топке под емкостью (котлом) с рабочим телом. Потом разогретое рабочее тело вводится в тепловой двигатель (поступает в цилиндр) , и совершает полезную работу, отдавая при этом теплоту.
К двигателям внутреннего сгорания (ДВС) относятся (например) всем с детства знакомые дизели и карбюраторные двигатели, у которых рабочее тело сжигается и выделяет тепло внутри системы (в цилиндре) .
И в том и в другом случае речь идет о термодинамических процессах, т.е. процессах, вызывающих температурные колебания (или вызываемых температурными колебаниями) внутри системы.
В общем случае суть происходящего с точки зрения современной термодинамики описана здесь.
В начале XIX века талантливым французским инженером Сади Карно (1796-1832) были изучены термодинамические процессы, имеющие место в тепловых машинах, использующих в качестве рабочего тела идеальный газ. При этом все процессы в машинах рассматривались им как равновесные (обратимые) .
Обратимый процесс – это такой процесс, который протекает настолько медленно, что его можно рассматривать как последовательный переход от одного равновесного состояния к другому и т. д., причём весь этот процесс можно провести в обратном направлении без изменения совершённой работы и переданного количества теплоты. (Следует отметить, что все реальные процессы необратимы).
Целью исследований Карно было определение условий, при которых можно получить максимальную работу из теплоты, подведенной к тепловой машине, т. е. наиболее эффективно преобразовать тепловую энергию в механическую.
В конце XVIII – начале XIX века единственным типом тепловых машин, используемых человечеством в практических целях, являлись двигатели внешнего сгорания – т. е. паровые машины. КПД этих машин был чрезвычайно низким – не более 2 %, при этом не существовало какой-либо убедительной теории, указывающей пути к повышению их эффективности.

Карно провел тщательный анализ различных способов преобразования теплоты в работу на примере идеализированной модели поршневой паровой машины, при этом результаты и выводы, сделанные им, оказались справедливыми для любого типа машин, использующими тепловую энергию для выполнения механической работы.
В результате теоретических умозаключений Карно пришел к выводу, что максимального эффекта от преобразования теплоты в механическую энергию можно достичь, используя круговой цикл, состоящий из четырех последовательных процессов - изотермического, адиабатного, изотермического и опять адиабатного, который завершал цикл, возвращая систему к исходному состоянию.
Эта последовательность термодинамических процессов в тепловой машине получила название идеальный цикл Карно .
Изготовить реальный двигатель, преобразующий энергию тепла в механическую энергию строго по циклу, предложенному Карно, невозможно по технологическим причинам, поэтому цикл Карно считается неосуществимым и идеальным.
Сади Карно ввел в научную терминологию основные понятия термодинамики - идеальная тепловая машина, идеальный цикл, обратимость и необратимость термодинамических процессов.
В начале XIX века использовались лишь примитивные паровые машины, КПД которых не превышал несколько процентов, поскольку не существовало теории, способной разъяснить способы повышения эффективности использования тепловой энергии в двигателях. Работа Карно послужила первым путеводителем для инженеров в поисках эффективного использования теплоты в двигателях.
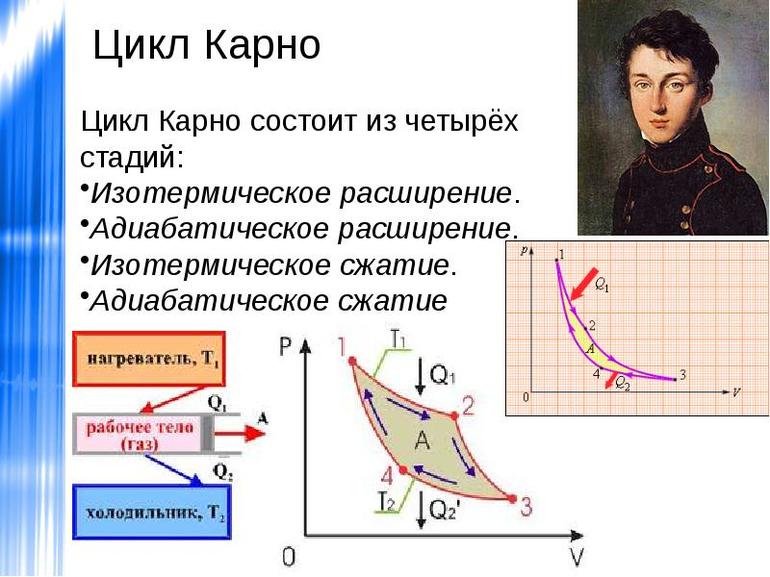
Последовательность процессов в цикле Карно
Рассмотрим предложенную Карно последовательность термодинамических процессов, получившую название идеальный цикл Карно.
Как известно, механическая работа может совершаться термодинамической системой лишь в том случае, когда протекает процесс, сопровождающийся изменением объема рабочего тела, т. е. изотермический, изобарный или адиабатный. При этом вся тепловая энергия может быть преобразована в работу лишь при изотермическом процессе (при изобарном и адиабатном процессе часть теплоты расходуется на изменение внутренней энергии рабочего тела) .
При изохорном процессе (протекающем при неизменном объеме рабочего тела) превращения теплоты в механическую работу исключается.
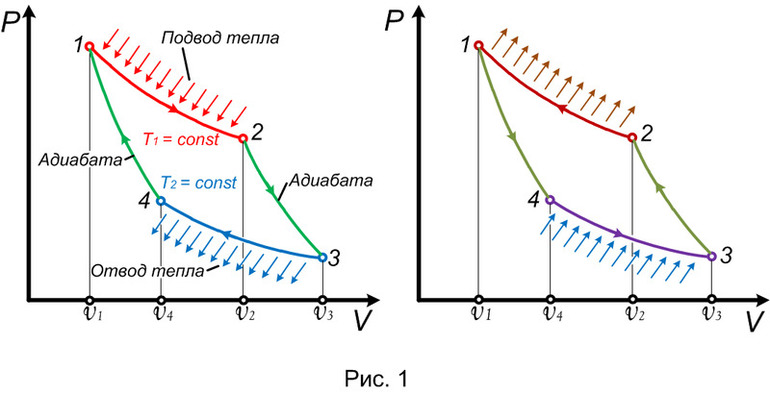
В исходном состоянии идеального цикла Карно рабочее тело (идеальный газ) имеет некоторые параметры p1 , V1 , T1 .
К рабочему телу от внешнего источника, называемого нагревателем , подводится теплота, которую система (тепловая машина) начинает использовать по изотермическому процессу.
Как отмечалось выше, при изотермическом процессе переменными являются два основных параметра рабочего тела - давление и объем, соотношение между которым обратно пропорционально (закономерность Бойля-Мариотта) . При этом вся подведенная к рабочему телу теплота расходуется исключительно на совершение механической работы; внутренняя энергия рабочего тела остается неизменной и затрат теплоты, полученной от внешнего нагревателя, не требует. Поэтому выбор первого термодинамического процесса в цикле Карно по изотерме вполне логичен - это позволяет максимально использовать полученное от нагревателя тепло для выполнения механической работы.
По окончании изотермического процесса рабочее тело имеет параметры p2 , V2 , T1 .
Этот процесс цикла Карно на диаграмме (рис. 1) обозначен цифрами 1-2.
Поскольку цикл Карно является обратимым и круговым, т. е. все протекающие в нем термодинамические процессы должны возвращать рабочее тело к исходным параметрам, становится очевидным, что в цикле должен присутствовать еще хотя бы один изотермический процесс. При этом его течение должно сопровождаться охлаждением рабочего тела, т. е. передачей теплоты от системы во внешнюю среду, иначе к точке с начальными параметрами не вернуться. Если сразу после первого процесса запустить второй изотермический процесс, то суммарная работа цикла будет минимальна, поскольку площадь графика, характеризующая выполненную системой механическую работу (на рис. 1 заштрихована) будет мала или вообще равна нулю (если прямая и обратная изотермы совпадают) .

По этой причине С. Карно в качестве второго термодинамического процесса для своего цикла применил адиабатный процесс, протекающий без теплообмена системы с внешней средой. При этом работа выполняется за счет изменения внутренней энергии рабочего тела, которое продолжает расширяться и охлаждаться до температуры Т2 . На диаграмме цикла Карно этот участок заключен между цифрами 2-3.
Использование адиабатного процесса вслед за изотермическим позволяет получить от системы некоторую механическую работу уже без подвода теплоты от нагревателя, за счет использования внутренней энергии рабочего тела.
Параметры рабочего тела по окончанию этого процесса - p3 , V3 , T2 .
Следующим звеном цикла Карно является второй изотермический процесс, который, как уже рассматривалось выше, должен быть отрицательным, т. е. сопровождаться передачей тепла от рабочего тела во внешнюю среду другому телу, называемому в данном случае холодильником .
На диаграмме цикла этот процесс обозначен цифрами 3-4.
Течение процесса сопровождается уменьшением объема и увеличением давления рабочего тела (сжатием) , при этом его температура остается постоянной за счет отдачи тепла холодильнику.
Параметры рабочего тела по окончании этого процесса - p4 , V4 , T2 .
Заключительный процесс цикла Карно, возвращающий систему в исходное состояние с начальными параметрами p1 , V1 , T1 - адиабатный.
Передача тепла холодильнику прекращается. При этом рабочее тело продолжает уменьшаться в объеме (сжиматься) , за счет совершения над ним некоторой внешней работы, которая для процесса является отрицательной.
Внутренняя энергия рабочего тела при этом увеличивается, поскольку часть внешней работы расходуется на его нагрев.
Этот процесс на диаграмме обозначен цифрами 4-1.
Анализ полученной Карно круговой p-V диаграммы цикла показывает, что системой выполнена механическая работа, величина которой характеризуется площадью, заключенной между кривой, ограниченной точками 1-2-3 и кривой, ограниченной точками 3-4-1. При этом вся выполненная системой работа будет равна сумме работ, выполненных в течение каждого из четырех последовательных термодинамических процессов, перечисленных выше.
Очевидно, что работа, выполненная рабочим телом в течение прямого и обратного адиабатных процессов равна по величине, но имеет разный знак (положительная в первом процессе, и отрицательная во втором) , т. е. сумма этих работ равна нулю. А работа, выполненная в течение прямого изотермического процесса больше, чем работа, совершенная во время обратного изотермического процесса.
Графически это поясняется разной площадью диаграммы, заключенной между абсциссой и соответственно первой и второй изотермой. Чем выше расположена первая изотерма на диаграмме относительной второй (обратной) изотермы, тем большую работу совершит рабочее тело.
Если рассмотреть T-V диаграмму процесса, то она будет представлять плоскую фигуру (например, ромб) , в которой две изотермы (прямая и обратная) параллельны одной из осей (температурной) , а адиабаты будут параллельны друг другу.
Из этого следует, что выполненная системой полезная работа будет тем больше, чем больше разница между температурой нагревателя и температурой холодильника, т. е. чем больше перепад температур между Т1 и Т2 (расстояние между верхней и нижней изотермой на T-V диаграмме) .
Математический анализ предложенной Сади Карно модели идеального цикла показывает, что максимальный термический КПД тепловой машины может быть определен из соотношения:
где: Т1 и Т2 – температура рабочего тела (газа) соответственно в начале и конце цикла.
Эта простая формула позволяет сделать два основных вывода - о пути повышения КПД тепловых машин и о том, что невозможно создать тепловую машину, коэффициент полезного действия которой будет равен единице, т. е. 100 %. Действительно – дробь Т2/Т1 может быть равна нулю лишь в том случае, если ее числитель равен нулю, либо знаменатель равен бесконечности. И то и другое – нереально, поскольку невозможно охладить материальное тело до температуры абсолютного нуля, и невозможно начальную температуру рабочего тела сделать бесконечной, поскольку само понятие тела в этом случае потеряет смысл; кроме того - невозможно изготовить реальный двигатель, детали и узлы которого способны выдержать такую температуру.

Цикл Карно является эталоном, к которому стремятся инженеры, проектирующие тепловые машины. В условиях реальных температур, верхний предел которых определяется прочностью материалов, а нижний соответствует температуре окружающей среды, термический КПД цикла Карно может достигать величины 0,7…0,8.
Любой реальный тепловой двигатель будет тем совершеннее, чем ближе его КПД к расчетному КПД цикла Карно, протекающего в тех же температурных границах.
Устройство, имеющее способность преобразовывать полученную теплоту в механическую работу носит название теплового двигателя. В таких машинах механическая работа совершается в процессе расширения вещества, называющегося рабочим телом. Его роль обычно исполняют газообразные вещества, вроде паров бензина, воздуха и водяного пара.
Рабочее тело приобретает или отдает тепловую энергию при теплообмене с телами, которые имеют внушительный запас внутренней энергии. Такие тела называют тепловыми резервуарами.
Исходя из первого закона термодинамики, можно сделать вывод, что полученное газом количество теплоты Q полностью преобразуется в работу A в условиях изотермического процесса, при котором внутренняя энергия не претерпевает изменений ( Δ U = 0 ) :
Однако, подобный однократный акт превращения теплоты в работу для техники не представляет интереса. Существующие тепловые двигатели, такие как паровые машины, двигатели внутреннего сгорания и им подобные, работают циклически. Необходимо периодическое повторение процесса теплопередачи и преобразования полученной теплоты в работу. Чтобы данное условие выполнялось, рабочее тело должно совершать круговой процесс или же термодинамический цикл, при котором исходное состояние с периодически восстанавливается. На рисунке 3 . 11 . 1 в виде диаграммы ( p , V ) газообразного рабочего тела с помощью замкнутых кривых проиллюстрированы круговые. В условиях расширения газ производит положительную работу A 1 , эквивалентную площади под кривой a b c . При сжатии газ совершает отрицательную работу A 2 , равную по модулю площади под кривой c d a . Полная работа за цикл A = A 1 + A 2 на диаграмме ( p , V ) равняется площади цикла. Работа A положительна, в том случае, если цикл проходит по часовой стрелке, и A отрицательна, когда цикл проходит в противоположном направлении.

Рисунок 3 . 11 . 1 . Круговой процесс на диаграмме ( p , V ) . a b c – кривая расширения, c d a – кривая сжатия. Работа A в круговом процессе равна площади фигуры a b c d .
Все круговые процессы обладают общей чертой. Они не могут привестись в действие при контакте рабочего тела только с одним тепловым. Их минимальное число должно быть равным двум.
Тепловой резервуар, обладающий более высоким значением температуры, носит название нагревателя, а с более низким – холодильника.
Рабочее тело при совершении кругового процесса получает от нагревателя некоторую теплоту Q 1 > 0 и теряет, отдавая холодильнику, количество теплоты Q 2 0 . Для полного полученного рабочим телом за цикл количества теплоты Q справедливо следующее выражение:
Q = Q 1 + Q 2 = Q 1 - Q 2 .
Совершая цикл, рабочее тело приходит в свое первоначальное состояние, из чего можно сделать вывод, что изменение его внутренней энергии равняется Δ U = 0 . Основываясь на первом законе термодинамики, запишем:
Из этого следует:
Работа A , которую рабочее тело совершает за цикл, эквивалентна полученному за этот же цикл количеству теплоты Q .
Коэффициентом полезного действия или же КПД η теплового двигателя называют отношение работы A к полученному рабочим телом за цикл от нагревателя количеству теплоты Q 1 , то есть:
η = A Q 1 = Q 1 - Q 2 Q 1 .
Рисунок 3 . 11 . 2 . Модель термодинамических циклов.
Коэффициент полезного действия теплового двигателя демонстрирует, какая доля тепловой энергии, которую получило рабочее тело от нагревателя, преобразовалась в полезную работу. Оставшаяся часть ( 1 – η ) была без пользы передана холодильнику. Коэффициент полезного действия тепловой машины не может быть больше единицы η 1 . На рисунке 3 . 11 . 3 проиллюстрирована энергетическая схема тепловой машины.

Рисунок 3 . 11 . 3 . Энергетическая схема тепловой машины: 1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q 1 > 0 , A > 0 , Q 2 0 ; T 1 > T 2 .
Виды тепловых двигателей
В технике свое применение находят двигатели, использующие круговые процессы. Рисунок 3 . 11 . 3 демонстрирует нам циклы, применяемые в бензиновом карбюраторном и в дизельном двигателях. Они оба в качестве рабочего тела используют смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания включает в себя две изохоры ( 1 – 2 , 3 – 4 ) и две адиабаты ( 2 – 3 , 4 – 1 ) , дизельного двигателя -две адиабаты ( 1 – 2 , 3 – 4 ) , одну изобару ( 2 – 3 ) и одну изохору ( 4 – 1 ) . Реальный КПД (коэффициент полезного действия) у карбюраторного двигателя составляет около 30 % , у дизельного двигателя – приблизительно 40 % .
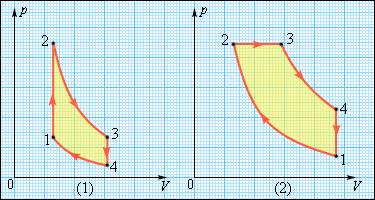
Рисунок 3 . 11 . 4 . Циклы карбюраторного двигателя внутреннего сгорания ( 1 ) и дизельного двигателя ( 2 ) .
Цикл Карно
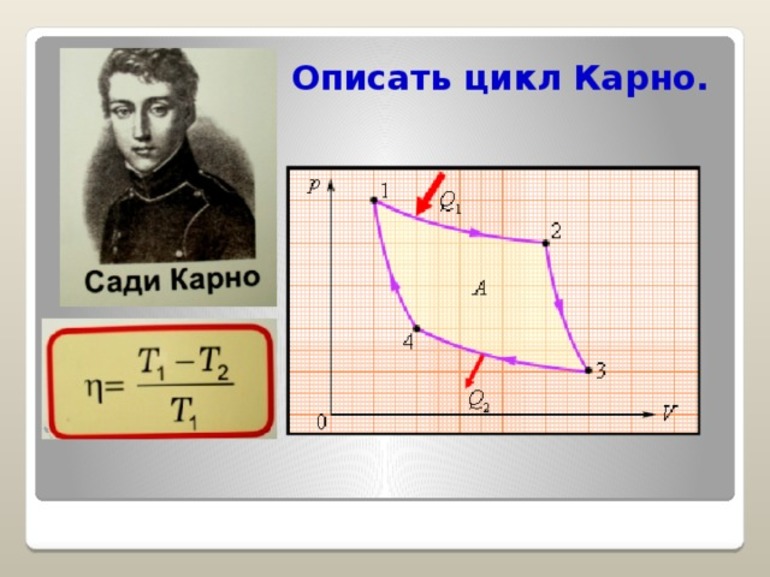
Круговой процесс, изображенный на рисунке 3 . 11 . 5 , состоящий из двух изотерм и двух адиабат был назван циклом Карно в честь открывшего его в 1824 году французского инженера. Данное явление впоследствии оказало колоссальное влияние на развитие учения о тепловых процессах.

Рисунок 3 . 11 . 5 . Цикл Карно.
Находящийся в цилиндре, под поршнем, газ совершает цикл Карно. На участке изотермы ( 1 – 2 ) он приводится в тепловой контакт с нагревателем, обладающим некоторой температурой T 1 . Газ изотермически расширяется, при этом к нему подводится эквивалентное совершенной работе A 12 количество теплоты Q 1 = A 12 . После этого на участке адиабаты ( 2 – 3 ) газ помещается в адиабатическую оболочку и продолжает процесс расширения при отсутствующем теплообмене. На данной части цикла газ совершает работу A 23 > 0 . Его температура при адиабатическом расширении снижается до величины T 2 . На идущем следующим участке изотермы ( 3 – 4 ) газ приводится в тепловой контакт с холодильником в условиях температуры T 2 T 1 . Производится процесс изотермического сжатия. Газом совершается некоторая работа A 34 0 и отдается тепло Q 2 0 , эквивалентное произведенной им работе A 34 . Его внутренняя энергия не претерпевает изменений. На последнем оставшемся участке адиабатического сжатия газ снова помещают в адиабатическую оболочку. При сжатии его температура вырастает до величины T 1 , также совершается работа A 41 0 . совершаемая газом за цикл полная работа A эквивалентна сумме работ на отдельных участках:
A = A 12 + A 23 + A 34 + A 41 .
На диаграмме ( p , V ) данная работа равняется площади цикла.
Процессы на любом из участков цикла Карно квазистатичны. Например, оба участка 1 – 2 и 3 – 4 , относящихся к изотермическим, производятся при пренебрежительно малой разности температур рабочего тела, то есть газа, и теплового резервуара, будь то нагреватель или холодильник.
Исходя из первого закона термодинамики, можно заявить, что работа газа в условиях адиабатического расширения или сжатия эквивалентна падению значения Δ U его внутренней энергии. Для 1 моля газа верно следующее выражение:
A = - ∆ U = - C V ( T 2 - T 1 ) ,
в котором T 1 и T 2 представляют собой начальную и конечную температуры рабочего тела.
Из этого следует, что работы, совершаемые газом на двух адиабатических участках цикла Карно, противоположны по знакам и одинаковы по модулю:
Коэффициент полезного действия η цикла Карно может рассчитываться с помощью следующих соотношений:
η = A Q 1 = A 12 + A 34 Q 12 = Q 1 - Q 2 Q 1 = 1 - Q 2 Q 1 .
С. Карно выразил коэффициент полезного действия цикла через величины температур холодильника T 2 и нагревателя T 1 :
η = T 1 - T 2 T 1 = 1 - T 2 T 1 .
Цикл Карно примечателен тем, что ни на одном из его участков тела, обладающие различными температурами, не соприкасаются. Любое состояние рабочего тела в цикле является квазиравновесным, что означает его бесконечную близость к состоянию теплового равновесия с окружающими объектами, то есть тепловыми резервуарами или же термостатами. В цикле Карно исключен теплообмен в условиях конечной разности температур рабочего тела и окружающей среды (термостатов), если тепло имеет возможность переходить без совершения работы. По этой причине любые другие возможные круговые процессы проигрывают ему в эффективности при заданных температурах нагревателя и холодильника:
η К а р н о = η m a x
Рисунок 3 . 11 . 6 . Модель цикла Карно.
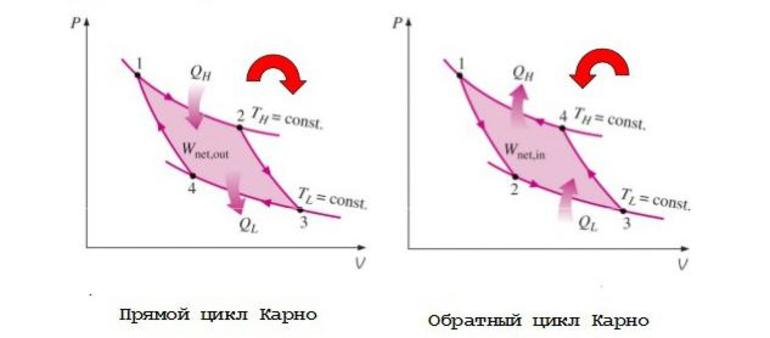
Каждый участок цикла Карно и цикл в целом могут проходиться в обоих направлениях.
Обход цикла по часовой стрелке соответствует тепловому двигателю, в котором полученное рабочим телом тепло частично преобразуется в полезную работу. Обход против часовой стрелки соответствует холодильной машине, где некое количество теплоты отходит от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Именно поэтому идеальное устройство, работающее по циклу Карно, носит название обратимой тепловой машины.
В реально существующих холодильных машинах применяются разные циклические процессы. Любой холодильный цикл на диаграмме ( p , V ) обходятся против часовой стрелки. На рисунке 3 . 11 . 7 проиллюстрирована энергетическая схема холодильной машины.

Рисунок 3 . 11 . 7 . Энергетическая схема холодильной машины. Q 1 0 , A > 0 , Q 2 > 0 , T 1 > T 2 .
Работающее по холодильному циклу устройство может обладать двояким предназначением.
Если полезным эффектом является отбор некоторого количества тепла Q 2 от охлаждаемых тел, к примеру, от продуктов в камере холодильника, то такое устройство является обычным холодильником.
Эффективность работы холодильника может быть охарактеризована следующим отношением:
Таким образом, эффективность работы холодильника представляет собой количество тепла, отбираемого от охлаждаемых тел на 1 д ж о у л ь затраченной работы. В условиях подобного определения β х может быть, как больше, так и меньше единицы. Для обращенного цикла Карно справедливо выражение:
β x = T 2 T 1 - T 2 .
В случае, когда полезным эффектом является передача некоего количества тепла
| Q 1 | нагреваемым телам, чьим примером может выступать воздух в помещении, то такое устройство называется тепловым насосом.
Эффективность β Т теплового насоса может быть определена с помощью отношения:
То есть она может определяться количеством теплоты, передаваемым более теплым телам на 1 д ж о у л ь затраченной работы. Из первого закона термодинамики следует:
Следовательно, β Т всегда больше единицы. Для обращенного цикла Карно справедливо следующее выражение:
В термодинамике цикл Карно? или процесс Карно — это обратимый круговой процесс, состоящий из двухадиабатических и двух изотермических процессов. В процессе Карно термодинамическая система выполняет механическую работу и обменивается теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником.
Поскольку обратимые процессы могут осуществляться лишь с бесконечно малой скоростью, мощность тепловой машины в цикле Карно равна нулю. Мощность реальных тепловых машин не может быть равна нулю, поэтому реальные процессы могут приближаться к идеальному обратимому процессу Карно только с большей или меньшей степенью точности. В цикле Карно тепловая машина преобразует теплоту в работу с максимально возможным коэффициентом полезного действия из всех тепловых машин, у которых максимальная и минимальная температуры в рабочем цикле совпадают соответственно с температурами нагревателя и холодильника в цикле Карно.

Цикл Карно в координатах T-s
Одной из координат в этом графике является ЭНТРОПИЯ – s.
Энтропия выражается функцией:

,
где q – подведенная к рабочему телу теплота, T – его температура при изотермическом процессе.
Для цикла Карно в T,s - диаграмме подведенная q1 и отведенная q2 теплота к рабочему телу представляют площади под изотермическими процессами, которые соответствуют прямоугольникам со сторонами: для q1 - с Т1 и Δs, для q2 - с T2 и Δs. Величины q1 и q2 определяются по формулам изотермического процесса:
 |
 |
Работа цикла Карно равна разности подведенной и отведенной теплоты
 |
В соответствии с последним выражением получить работу возможно только при наличии разности температур у горячего и холодного источников теплоты. Максимальная работа Цикла Карно теоретически была бы при Т2=0, но в качестве холодного источника в тепловых машинах, как правило, используется окружающая среда (вода, воздух) с температурой около 300 К. Кроме этого, достижение абсолютного нуля в природе невозможно (этот факт относится к третьему закону термодинамики). Таким образом, в цикле Карно не вся теплота q1 превращается в работу, а только ее часть, Оставшаяся после получения работы теплота q2, отдается холодному источнику, и при заданных Т1 и Т2 она не может быть использована для получения работы, величина q2 является тепловыми потерями (тепловым отбросом) цикла.
Пусть тепловая машина состоит из: 1) нагревателя с температурой , 2) холодильника с температурой и 3) рабочего тела.
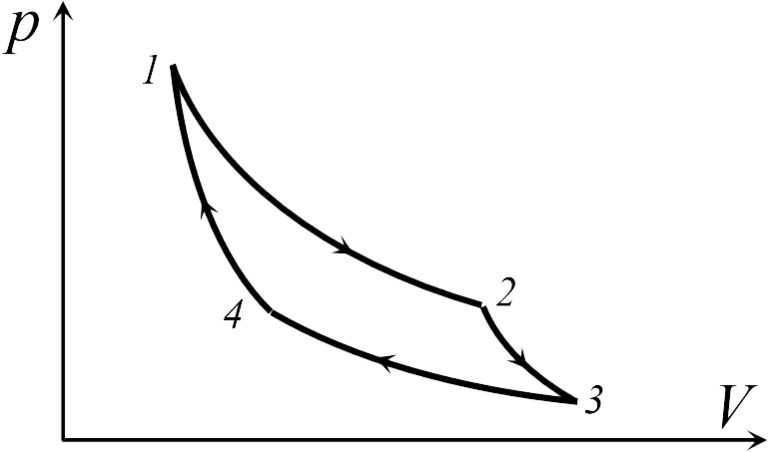
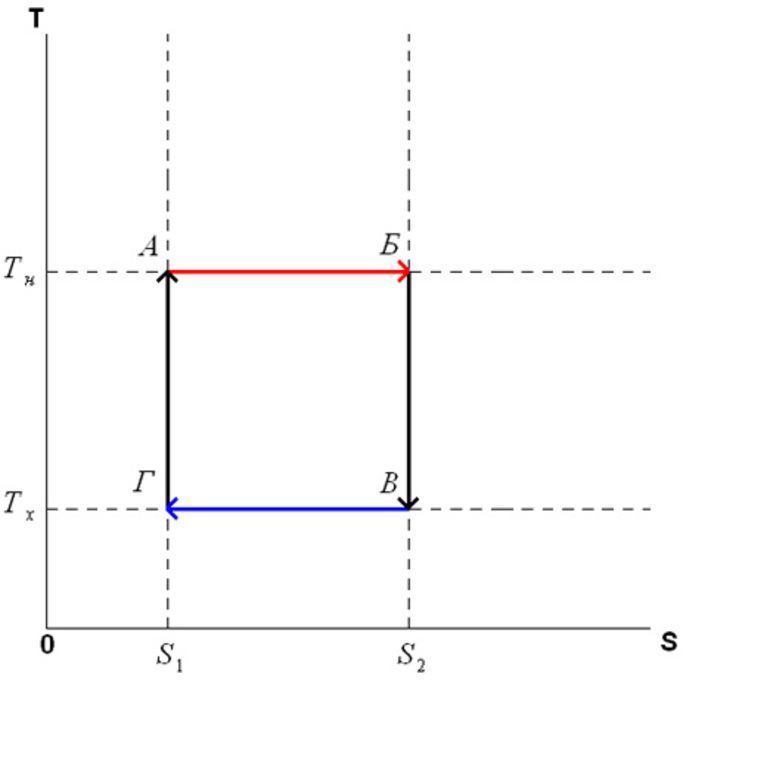
Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две — при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах T (температура) и S (энтропия).
1. Изотермическое расширение (на рис. 1 — процесс A→Б). В начале процесса рабочее тело имеет температуру , то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты . При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.

2. Адиабатическое расширение (на рис. 1 — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника , тело совершает механическую работу, а энтропия остаётся постоянной.
3. Изотермическое сжатие (на рис. 1 — процесс В→Г). Рабочее тело, имеющее температуру , приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты . Над телом совершается работа, его энтропия уменьшается.
4. Адиабатическое сжатие (на рис. 1 — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.
Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

.
Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику

.
Отсюда коэффициент полезного действия тепловой машины Карно равен

.
Из последнего выражения следует, что КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела. Этот результат составляет содержание первой теоремы Карно. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.
Поэтому максимальный КПД любой тепловой машины не может превосходить КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Это утверждение называется второй теоремой Карно. Оно даёт верхний предел КПД любой тепловой машины и позволяет оценить отклонение реального КПД от максимального, то есть потери энергии вследствие неидеальности тепловых процессов.
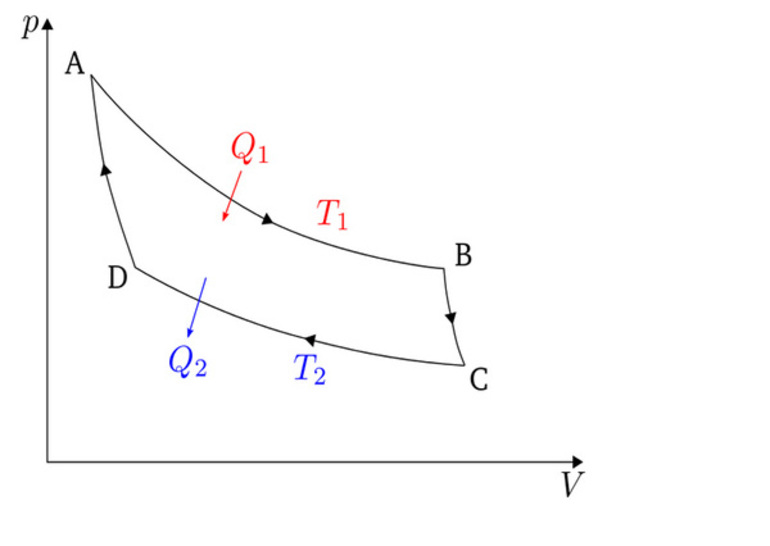
Цикл Карно может быть представлен и в координатах P (давление рабочего тела) и V (объем рабочего тела). Понятно, что рабочее тело – это пар в турбине, или газ в цилиндре двигателя внутреннего сгорания.

Рис. 2. Цикл Карно в координатах P и V
Для того чтобы цикл был обратимым, в нём должна быть исключена передача теплоты при наличии разности температур, иначе нарушается условие адиабатичности процесса. Поэтому передача теплоты должна осуществляться либо в изотермическом процессе (как в цикле Карно), либо в эквидистантном процессе (обобщённый цикл Карно или, для примера, его частный случай Цикл Брайтона). Для того чтобы менять температуру рабочего тела от температуры нагревателя до температуры холодильника и обратно, необходимо использовать либо адиабатические процессы (они идут без теплообмена и, значит, не влияют на энтропию), либо циклы с регенерацией тепла при которых нет передачи тепла при разности температур. Мы приходим к выводу, что любой обратимый цикл может быть сведён к циклу Карно.
Примером обратимого цикла, не являющегося циклом Карно, но интегрально совпадающим с ним, является идеальный цикл Стирлинга: в двигателе Стирлинга добавлен регенератор, обеспечивающий полное приближение цикла к циклу Карно с достижением обратимости и тех же величин КПД.
Если же в цикле возникает передача теплоты при наличии разности температур, а таковыми являются все технические реализации термодинамических циклов, то цикл утрачивает свойство обратимости. Иначе говоря, посредством отведённой в цикле механической работы становится невозможным получить исходную теплоту. КПД такого цикла будет всегда меньше, чем КПД цикла Карно.

Краткая биография
Николя Леонард Сади Карно, сын высокопоставленного военачальника Лазаря Николая Маргарита Карно, родился в Париже в 1796 году. Его отец ушёл из армии в 1807 году, чтобы обучить Николаса и его брата Ипполита — оба получили широкое домашнее образование, включающее:
- науку;
- искусство;
- иностранные языки;
- музыку.
В 1812 году 16-летний Николас Карно был принят в Высшую политехническую школу в Париже. Его учителями были Джозеф Луи Гей-Люссак, Симеон Дени Пуассон и Андре-Мари Ампер, а сокурсниками — будущие учёные Клод-Луи Навье и Гаспар-Гюстав Кориолис. Во время учёбы в школе Карно проявил особый интерес к теории газов и решению задач промышленной инженерии. После окончания университета он поступил во французскую армию в качестве военного инженера и прослужил до 1814 года.
Освободившись от ограничений военной жизни, Карно начал широкий спектр исследований, которые продолжались, несмотря на многочисленные перерывы, до само́й смерти. В дополнение к частным занятиям он посещал курсы:
- в Сорбонне;
- Коллеж де Франс.
- в Школе шахт;
- в Консерватории искусств.
В последней он стал другом Николаса Клемента, который преподавал курс прикладной химии, а затем занимался важными исследованиями паровых двигателей и теории газов.
Одним из особых интересов Карно было промышленное развитие, которое он изучал во всех его аспектах. Он часто посещал фабрики и мастерские, читал новейшие теории политической экономии и оставлял в своих заметках подробные предложения по таким актуальным проблемам, как налоговая реформа. Помимо этого, его деятельность и способности охватили математику и изобразительное искусство.
После публикации Карно продолжил исследования, выводы из которых сохранились в его рукописных заметках. Однако реорганизация корпуса Генерального штаба вынудила Карно вернуться на службу в 1827 году в звании капитана. После менее чем годовой работы в качестве военного инженера Карно ушёл в отставку навсегда и вернулся в Париж. Он снова сосредоточил своё внимание на проблемах конструкции двигателя и теории тепла.
Работы учёного
- изотермическое расширение при подаче пара в цилиндр;
- адиабатическое расширение;
- изотермическое сжатие в конденсаторе.
Эссе как по методам, так и по целям похоже на многие статьи, опубликованные между 1818 и 1824 годами такими учёными, как Хашетт, Навье, Пети и Комбес. Работа Карно, однако, отличается своим тщательным, чётким анализом используемых единиц и концепций и тем, что он использует как адиабатическую рабочую стадию, так и изотермическую стадию. Отточенный характер, в отличие от его грубых заметок, делало её предназначенной для публикации, хотя она оставалась неизвестной в рукописи до 1966 года.
- Существует ли установленный предел для движущей силы тепла и, следовательно, для улучшения паровых двигателей?
- Есть ли агенты предпочтительнее пара в производстве этой движущей силы?
Обе проблемы были своевременными и, хотя французские инженеры исследовали их в течение десятилетия, не было принято общепринятых решений. В отсутствии чёткой концепции эффективности предлагаемые конструкции паровых двигателей оценивались в основном по практичности, безопасности и экономии топлива.
Некоторые инженеры считали воздух, углекислоту и спирт лучшим рабочим веществом, чем пар. Обычным подходом к этим проблемам было либо эмпирическое исследование расхода топлива и выходной мощности отдельных двигателей, либо применение математической теории газов к абстрактным операциям конкретного типа двигателя. В своём выборе проблем Карно был твёрд в этой инженерской традиции, однако его метод был радикально новым и являлся сутью его вклада в науку о тепле.
Предыдущая работа над паровыми машинами, как видел Карно, провалилась из-за отсутствия достаточно общей теории, применимой ко всем тепловым двигателям и основанной на установленных принципах. В качестве основы своего исследования Карно тщательно изложил три предпосылки. Первой была невозможность вечного движения — принцип, который долгое время предполагался в механике. В своей второй предпосылке Карно использовал калорийную теорию тепла, которая, несмотря на некоторую оппозицию, была принятой и самой развитой, доступной теорией тепла.
Принципы работы цикла Карно
Этот теоретический идеальный круговой термодинамический цикл был предложен французским физиком Сади Карно в 1824 году. Он обеспечивал максимально возможный предел эффективности для любого классического термодинамического двигателя во время преобразования тепла в работу или, наоборот, эффективность системы охлаждения при создании разницы температур при приложении работы к системе. Фактический термодинамический цикл является теоретической конструкцией.
Каждая термодинамическая система существует в определённом состоянии. Когда система проходит через ряд различных явлений и, наконец, возвращается в исходное состояние, говорят, что произошёл термодинамический цикл. В процессе прохождения этого цикла система может выполнять работу, например, перемещая поршень, тем самым действуя, как тепловой двигатель.
Из каких процессов состоит Цикл Карно при работе в качестве теплового двигателя:
Во время цикла произвольное количество энтропии S извлекается из горячего резервуара (нагревателя) и осаждается в холодном резервуаре. Поскольку в обоих резервуарах изменения объёма не происходит, они не работают, и в течение цикла количество энергии T h ΔS извлекается из горячего резервуара, а меньшее количество энергии T c ΔS откладывается в холодном резервуаре. Разница в двух энергиях (T h -T c) ΔS равна работе, проделанной двигателем.
Поведение двигателя или холодильника Карно лучше всего понять с помощью диаграммы, в которой координатами являются температура и энтропия. Термодинамическое состояние определяется точкой на графике с энтропией (S) в качестве горизонтальной оси и температуры (T) в качестве вертикальной оси. Для простой замкнутой системы любая точка на графике будет представлять конкретное состояние системы. Термодинамический процесс будет состоять из кривой, соединяющей начальное состояние (A) и конечное состояние (B), и представляющей собой количество тепловой энергии, передаваемой в процессе.
Если процесс движется к большей энтропии, площадь под кривой будет количеством тепла, поглощённого системой. Когда процесс движется к меньшей энтропии, это будет количество отводимого тепла. Для любого циклического процесса есть верхняя часть цикла и нижняя часть. Для цикла по часовой стрелке область под верхней частью будет тепловой энергией, поглощённой в течение цикла, тогда как область под нижней частью будет тепловой энергией, удалённой во время цикла.
Площадь внутри цикла будет тогда разницей между ними, но поскольку внутренняя энергия системы должна вернуться к своему первоначальному значению, эта разница должна быть объёмом работы, которую должна совершать системой за цикл.
Перевёрнутый цикл
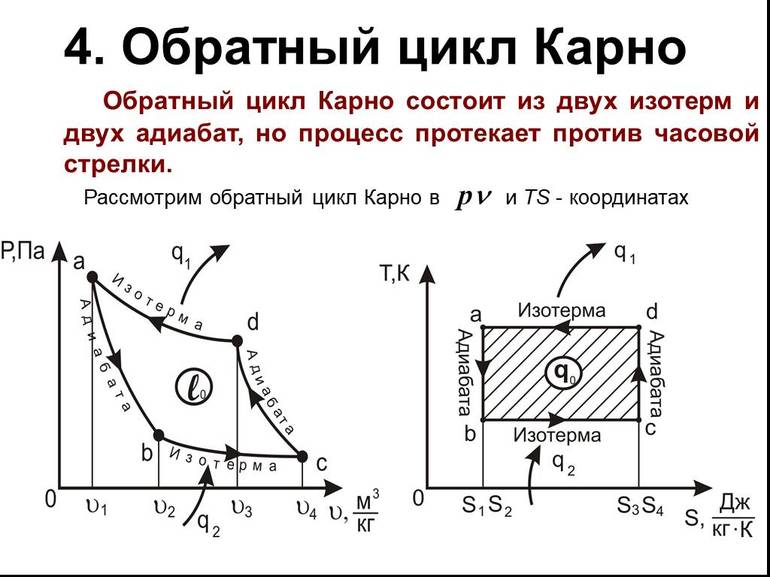
Описанный цикл теплового двигателя является полностью обратным циклом Карно. То есть все процессы, из которых он состоит, могут быть обращены вспять, и в этом случае цикл становится холодильным циклом Карно.
На этот раз цикл остаётся точно таким же, за исключением того, что направления любых тепловых и рабочих взаимодействий меняются местами. Тепло поглощается из низкотемпературного резервуара, отбрасывается в высокотемпературный резервуар, и для этого требуется работа. Диаграмма P-V обращённого цикла такая же, как и для цикла Карно, за исключением того, что направления процессов меняются местами.
Если же в цикле возникает передача теплоты при наличии разности температур, а такими являются все технические реализации термодинамических циклов, то цикл становится необратимым. КПД такого цикла будет всегда меньше, чем КПД цикла Карно.
Теорема Карно

Эта теорема является формальным утверждением этого факта: ни один двигатель, работающий между двумя тепловыми резервуарами, не может быть более эффективным, чем двигатель Карно, работающий между этими же резервуарами.
Следствие из теоремы Карно гласит: все реверсивные двигатели, работающие между одними и теми же тепловыми резервуарами, одинаково эффективны. Теоретический максимальный КПД теплового двигателя равён разнице в температуре между горячим и холодным резервуаром, делённой на абсолютную температуру горячего резервуара.
Исходя из этого, становится очевидным интересный факт: понижение температуры холодного резервуара будет иметь большее влияние на потолочную эффективность теплового двигателя, чем повышение температуры горячего резервуара на ту же величину. В реальном мире это труднодостижимо, так как холодный резервуар часто имеет существующую температуру окружающей среды.
Другими словами, максимальная эффективность достигается тогда, когда в цикле не создаётся новая энтропия, что было бы в случае, если, например, трение привело к рассеиванию работы в тепло. В противном случае, поскольку энтропия является функцией состояния, требуемый сброс тепла в окружающую среду для удаления избыточной энтропии приводит к (минимальному) снижению эффективности.
В мезоскопических тепловых двигателях работа за цикл обычно колеблется из-за теплового шума. Если цикл выполняется квазистатически, флуктуации исчезают даже на мезомасштабах. Но если цикл выполняется быстрее, чем время релаксации рабочего тела, колебания работы неизбежны. Тем не менее когда учтены рабочие и тепловые колебания, существует точное равенство, которое связывает экспоненциальное среднее значение работы, выполненной любым тепловым двигателем, и теплопередачу от горячей тепловой ёмкости.
Карно понимал, что в действительности невозможно создать термодинамический обратимый двигатель, поэтому реальные тепловые двигатели менее эффективны. Кроме того, реальные двигатели, работающие в этом цикле, встречаются редко. Но хотя прямой цикл французского учёного является идеализацией, его выражение эффективности всё ещё полезно для дальнейших исследований.
Примером обратимого цикла также является идеальный цикл Стирлинга. Существует и другие идеальные циклы, в которых коэффициент полезного действия определяется по той же формуле, что и для циклов Карно и Стирлинга, например, цикл Эрикссона.
Читайте также:


