Что такое бит память для хранения одного символа
Единицей измерения количества информации является бит – это наименьшаяединица.
1 Кб (килобайт) = 1024 байта= 2 10 байтов
1 Мб (мегабайт) = 1024 Кб = 2 10 Кб
1 Гб (гигабайт) = 1024 Мб = 2 10 Мб
1 Тб (терабайт) =1024 Гб = 2 10 Гб
Формулы, которые используются при решении типовых задач:
Информационный вес символа алфавита и мощность алфавита связаны между собой соотношением: N = 2 i .
i – информационный вес одного символа.
Основная литература:
- Босова Л. Л. Информатика: 7 класс. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2017. – 226 с.
Дополнительная литература:
- Босова Л. Л. Информатика: 7–9 классы. Методическое пособие. // Босова Л. Л., Босова А. Ю., Анатольев А. В., Аквилянов Н.А. – М.: БИНОМ, 2019. – 512 с.
- Босова Л. Л. Информатика. Рабочая тетрадь для 7 класса. Ч 1. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2019. – 160 с.
- Босова Л. Л. Информатика. Рабочая тетрадь для 7 класса. Ч 2. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2019. – 160 с.
- Гейн А. Г. Информатика: 7 класс. // Гейн А. Г., Юнерман Н. А., Гейн А.А. – М.: Просвещение, 2012. – 198 с.
Теоретический материал для самостоятельного изучения.
Что же такое символ в компьютере? Символом в компьютере является любая буква, цифра, знак препинания, специальный символ и прочее, что можно ввести с помощью клавиатуры. Но компьютер не понимает человеческий язык, он каждый символ кодирует. Вся информация в компьютере представляется в виде нулей и единичек. И вот эти нули и единички называются битом.
Информационный вес символа двоичного алфавита принят за минимальную единицу измерения информации и называется один бит.
Алфавит любого понятного нам языка можно заменить двоичным алфавитом. При этом мощность исходного алфавита связана с разрядностью двоичного кода соотношением: N = 2 i .
Эту формулу можно применять для вычисления информационного веса одного символа любого произвольного алфавита.
Рассмотрим пример:
Алфавит древнего племени содержит 16 символов. Определите информационный вес одного символа этого алфавита.
Составим краткую запись условия задачи и решим её:
16 = 2 i , 2 4 = 2 i , т. е. i = 4
Ответ: i = 4 бита.
Информационный вес одного символа этого алфавита составляет 4 бита.
Математически это произведение записывается так: I = К · i.
32 = 2 i , 2 5 = 2 i , т.о. i = 5,
I = 180 · 5 = 900 бит.
Ответ: I = 900 бит.
I = 23 · 8 = 184 бита.
Как и в математике, в информатике тоже есть кратные единицы измерения информации. Так, величина равная восьми битам, называется байтом.
Бит и байт – это мелкие единицы измерения. На практике для измерения информационных объёмов используют более крупные единицы: килобайт, мегабайт, гигабайт и другие.
1 Кб (килобайт) = 1024 байта= 2 10 байтов
1 Мб (мегабайт) = 1024 Кб = 2 10 Кб
1 Гб (гигабайт) = 1024 Мб = 2 10 Мб
1 Тб (терабайт) =1024 Гб = 2 10 Гб
Материал для углубленного изучения темы.
Как текстовая информация выглядит в памяти компьютера.
Набирая текст на клавиатуре, мы видим привычные для нас знаки (цифры, буквы и т.д.). В оперативную память компьютера они попадают только в виде двоичного кода. Двоичный код каждого символа, выглядит восьмизначным числом, например 00111111. Теперь возникает вопрос, какой именно восьмизначный двоичный код поставить в соответствие каждому символу?
Все символы компьютерного алфавита пронумерованы от 0 до 255. Каждому номеру соответствует восьмиразрядный двоичный код от 00000000 до 11111111. Этот код ‑ просто порядковый номер символа в двоичной системе счисления.
Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера, называется таблицей кодировки.Таблица для кодировки – это «шпаргалка», в которой указаны символы алфавита в соответствии порядковому номеру. Для разных типов компьютеров используются различные таблицы кодировки.
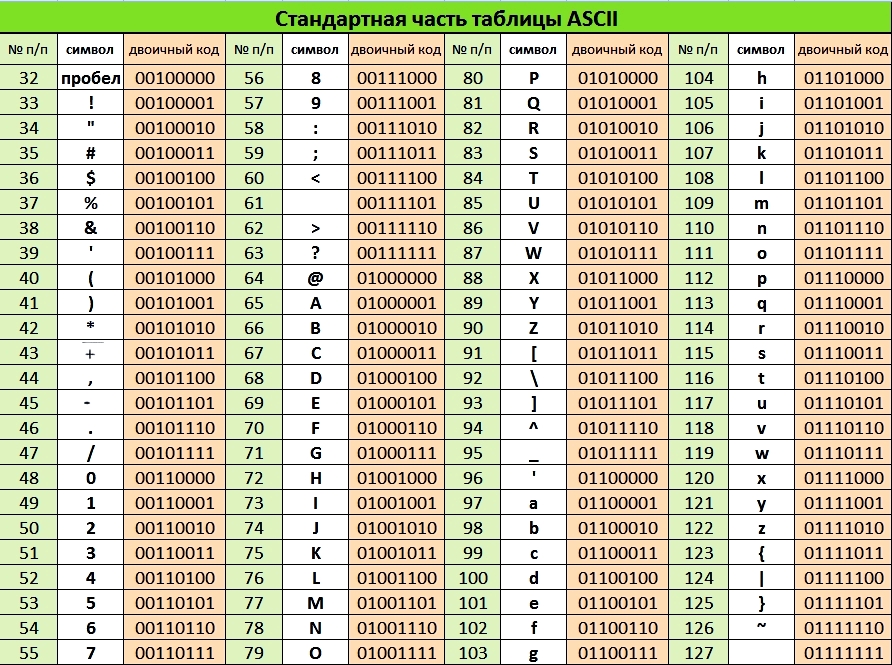
Таблица ASCII (или Аски), стала международным стандартом для персональных компьютеров. Она имеет две части.

В этой таблице латинские буквы (прописные и строчные) располагаются в алфавитном порядке. Расположение цифр также упорядочено по возрастанию значений. Это правило соблюдается и в других таблицах кодировки и называется принципом последовательного кодирования алфавитов. Благодаря этому понятие «алфавитный порядок» сохраняется и в машинном представлении символьной информации. Для русского алфавита принцип последовательного кодирования соблюдается не всегда.
Запишем, например, внутреннее представление слова «file». В памяти компьютера оно займет 4 байта со следующим содержанием:
01100110 01101001 01101100 01100101.
А теперь попробуем решить обратную задачу. Какое слово записано следующим двоичным кодом:
01100100 01101001 01110011 01101011?
В таблице 2 приведен один из вариантов второй половины кодовой таблицы АSСII, который называется альтернативной кодировкой. Видно, что в ней для букв русского алфавита соблюдается принцип последовательного кодирования.

Вывод: все тексты вводятся в память компьютера с помощью клавиатуры. На клавишах написаны привычные для нас буквы, цифры, знаки препинания и другие символы. В оперативную память они попадают в форме двоичного кода.
Из памяти же компьютера текст может быть выведен на экран или на печать в символьной форме.
Разбор решения заданий тренировочного модуля
Информационный вес символа алфавита и мощность алфавита связаны между собой соотношением: N = 2 i .
Давайте разберемся с этим, ведь нам придется измерять объем памяти и быстродействие компьютера.
Единицей измерения количества информации является бит – это наименьшая (элементарная) единица.
Байт – основная единица измерения количества информации.
Байт – довольно мелкая единица измерения информации. Например, 1 символ – это 1 байт.
Производные единицы измерения количества информации
1 килобайт (Кб)=1024 байта =2 10 байтов
1 мегабайт (Мб)=1024 килобайта =2 10 килобайтов=2 20 байтов
1 гигабайт (Гб)=1024 мегабайта =2 10 мегабайтов=2 30 байтов
1 терабайт (Гб)=1024 гигабайта =2 10 гигабайтов=2 40 байтов
Запомните, приставка КИЛО в информатике – это не 1000, а 1024, то есть 2 10 .
Методы измерения количества информации
Итак, количество информации в 1 бит вдвое уменьшает неопределенность знаний. Связь же между количеством возможных событий N и количеством информации I определяется формулой Хартли:
Алфавитный подход к измерению количества информации
Вероятностный подход к измерению количества информации
Этот подход применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:
I – количество информации,
N – количество возможных событий,
Pi – вероятность i-го события.
Задача 1.
Имеется 4 равновероятных события (N=4).
Задача 2.
Чему равен информационный объем одного символа русского языка?
В русском языке 32 буквы (буква ё обычно не используется), то есть количество событий будет равно 32. Найдем информационный объем одного символа. I=log2 N=log2 32=5 битов (2 5 =32).
Примечание. Если невозможно найти целую степень числа, то округление производится в большую сторону.
Задача 3.
Чему равен информационный объем одного символа английского языка?
Задача 4.
Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний (“включено” или “выключено”). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?
С помощью N лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2 N сигналов.
2 5 < 50 <2 6 , поэтому пяти лампочек недостаточно, а шести хватит. Значит, нужно 6 лампочек.
Задача 5.
Метеостанция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.
В данном случае алфавитом является множество чисел от 0 до 100, всего 101 значение. Поэтому информационный объем результатов одного измерения I=log2101. Но это значение не будет целочисленным, поэтому заменим число 101 ближайшей к нему степенью двойки, большей, чем 101. это число 128=2 7 . Принимаем для одного измерения I=log2128=7 битов. Для 80 измерений общий информационный объем равен 80*7 = 560 битов = 70 байтов.
Задача 6.
Определите количество информации, которое будет получено после подбрасывания несимметричной 4-гранной пирамидки, если делают один бросок.
Пусть при бросании 4-гранной несимметричной пирамидки вероятности отдельных событий будут равны: p1=1/2, p2=1/4, p3=1/8, p4=1/8.
Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:
I = -[1/2 * log2(1/2) + 1/4 * log2(1/4) + 1/8 * log(1/8) + 1/8 * log(1/8)] = 14/8 битов = 1,75 бита.
Задача 7.
В книге 100 страниц; на каждой странице - 20 строк, в каждой строке - 50 символов. Определите объем информации, содержащийся в книге.
Задача 8.
Оцените информационный объем следующего предложения:
Тяжело в ученье – легко в бою!
В течение последних трех десятилетий объем компьютерной памяти увеличивался в геометрической прогрессии, и с каждым следующим поколением появляется новый уровень единиц памяти и новые условия для изучения. Давайте рассмотрим эти единицы измерения.
Структурные единицы
Биты и байты являются основными структурными единицами памяти. "Бит" обозначает двоичный символ. Бит — это единица или ноль, включение или выключение, так сохраняется вся информация в компьютере. Байт состоит из восьми бит. Исходный объем информации, необходимой для кодирования одного символа текста, был изначально равен восьми битам или одному байту. Позже, по мере развития компьютерного оборудования, это число было стандартизировано.
По техническим причинам емкость компьютерной памяти выражается в единицах кратных числу два. Затем к этим кратным единицам добавили приставки для образования кратных единиц, чтобы обеспечить простой способ выражения очень большого количества бит и байтов.
Приставки СИ
Для измерения компьютерной памяти используются некоторые приставки международной системы единиц (СИ) для образования производных единиц для байта. Однако эти приставки не являются метрическими, поскольку байт состоит из восьми бит, а килобайт равен 1024 байтам.
Приставка единицы измерения памяти
Кило- (килобайт, КБ)
Мега- (мегабайт, МБ)
Гига- (гигабайт, ГБ)
Тера- (терабайт, ТБ)
Пета- (петабайт, ПБ)
Единицы измерения памяти
Компьютеры используют память в оперативном запоминающем устройстве (ОЗУ), которое временно хранит информацию, и в накопителях, данные на которых хранятся постоянно. ОЗУ позволяет компьютеру переключаться между программами и иметь большие файлы наготове для просмотра.
В зависимости от того, для чего используется ваш компьютер, вам, как правило, понадобится установить максимально возможное количество памяти. Тип и объем памяти, установленной на вашем компьютере, а также максимальный объем и скорость, которые можно нарастить, зависят от производителя и модели компьютера. Воспользуйтесь инструментом Crucial® Advisor™ или системным сканером, чтобы найти память, совместимую с вашим компьютером. Подробнее о том, какой объем памяти необходим вашему компьютеру, читайте здесь.

Накопители: при описании емкости жестких дисков и твердотельных накопителей используются одни те же термины, относящиеся к памяти. По мере увеличения объема файлов с видеороликами и очень большими фотографиями необходимо увеличение объема хранилищ. В настоящее время в продаже имеются твердотельные накопители разного объема, исчисляемого гигабайтами и терабайтами. Как и в случае с ОЗУ, вы можете использовать инструмент Crucial® Advisor™ или системный сканер для поиска твердотельного накопителя, совместимого с вашей системой.
Код ОГЭ по информатике: 2.1.3. Оценка количественных параметров информационных объектов. Объем памяти, необходимый для хранения объектов
Оценка количества информации
Впервые объективный подход к измерению количества информации был предложен американским инженером Р. Хартли в 1928 г. Позже, в 1948 г., этот подход обобщил создатель общей теории информации К. Шеннон.
По приведенной выше формуле можно рассчитать, какое количество информации I несет каждый из знаков этой системы. Если в алфавите знаковой системы N знаков, то каждый знак несет количество информации: I = log2 N

Текстовая информация состоит из букв, цифр, знаков препинания, различных специальных символов. Для кодирования текстовой информации используют различные коды. Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера, называется таблицей кодировки. Существуют различные таблицы кодировок текстовой информации.
Распространенная таблица кодировки ASCII (читается «аски», American Standard Code for Information Interchange — стандартный американский код для обмена информацией) использует 1 байт для кодов информации. Если код каждого символа занимает 1 байт (8 бит), то с помощью такой кодировки можно закодировать 2 8 = 256 символов.
Таблица ASCII состоит из двух частей. Первая, базовая часть, является международным стандартом и содержит значения кодов от 0 до 127 (для цифр, операций, латинского алфавита, знаков препинания). Вторая, национальная часть, содержит коды от 128 до 255 для символов национального алфавита, т. е. в национальных кодировках одному и тому же коду соответствуют различные символы.
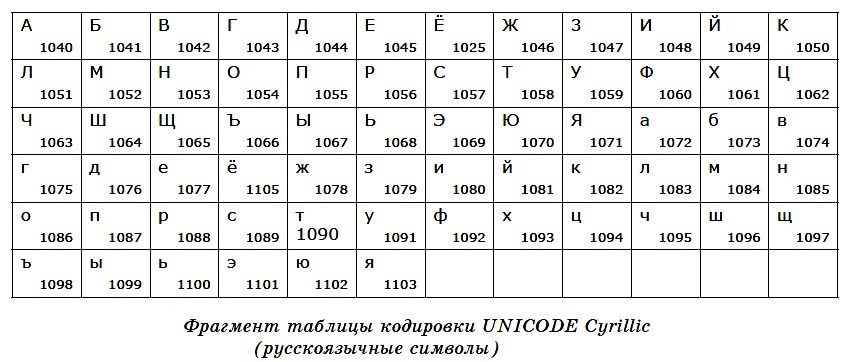
В настоящее время существует несколько различных кодировок второй части таблицы для кириллицы — КОИ8–Р, KOI8–U, Windows, MS–DOS, Macintosh, ISO. Наиболее распространенной является таблица кодировки Windows–1251. Из–за разнообразия таблиц кодировки могут возникать проблемы при переносе русского текста между компьютерами или различными программами.
Поскольку объем в 1 байт явно мал для кодирования разнообразных и многочисленных символов мировых алфавитов, была разработана система кодирования Unicode. В ней для кодирования символа отводится 2 байта (16 бит). Это означает, что система позволяет закодировать 2 16 = 65 536 символов. Полная спецификация стандарта Unicode включает в себя все существующие, вымершие и искусственно созданные алфавиты мира, а также множество математических, музыкальных, химических и прочих символов.
Количество графической информации
Растровое графическое изображение состоит из отдельных точек — пикселей, образующих строки и столбцы.
Основные свойства пикселя — его расположение и цвет. Значения этих свойств кодируются и сохраняются в видеопамяти компьютера.
Качество изображения зависит от пространственного разрешения и глубины цвета.
Разрешение — величина, определяющая количество точек (пикселей) на единицу площади.
Глубина цвета — объем памяти (в битах), используемой для хранения и представления цвета при кодировании одного пикселя растровой графики или видеоизображения.
Для графических изображений могут использоваться различные палитры — наборы цветов. Количество цветов N в палитре и количество информации I, необходимое для кодирования цвета каждой точки, связаны соотношением: N = 2 I
Чтобы определить информационный объем видеоизображения, необходимо умножить количество информации одного пикселя на количество пикселей в изображении: I = Iпикселя • X • Y, где Х — количество точек изображения по горизонтали, Y — количество точек изображения по вертикали.
Существует несколько цветовых моделей для количественного описания цвета. В основе модели RGB (сокращение от англ. Red, Green, Blue) лежат три основных цвета: красный, зеленый и синий. Все другие цвета создаются с помощью смешения их оттенков. Например, при смешивании красного и зеленого цветов получим желтый, красного и синего — пурпурный, зеленого и синего — бирюзовый. Если смешать все три основные цвета максимальной яркости, получим белый цвет.
Если один цвет имеет 4 оттенка, то общее количество цветов в модели RGB будет составлять 4 • 4 • 4 = 64. При 256 оттенках для каждого цвета общее количество возможных цветов будет равно 256 • 256 • 256 = 16 777 216 ≈ 16,7 млн.
В современных компьютерах для представления цвета обычно используются от 2–х до 4–х байт. Два байта (16 бит) позволяют различать 2 16 , то есть 65 536 цветов и оттенков. Такой режим представления изображений называется High Color. Четыре байта (32 бита) обеспечивают цветную гамму в 2 32 , то есть 4 294 967 296 цветов и оттенков (приблизительно 4,3 миллиарда). Такой режим называется True Color.
В графических редакторах применяются и другие цветовые модели. Например, модель CMYK — она основана на цветах, получающихся при отражении белого света от предмета: бирюзовом (англ. Cyan), пурпурном (англ. Magenta), желтом (англ. Yellow). Эта модель применяется в полиграфии, где чаще всего употребляется черный цвет (ключевой, англ. Key).

Измерение объемов звуковой информации
Звук является непрерывным сигналом. Для использования звука в компьютере его преобразуют в цифровой сигнал. Это преобразование называется дискретизацией: для кодирования звука производят его измерение с определенной частотой (несколько раз в секунду). частота дискретизации и точность представления измеренных значений определяют качество представления звука в компьютере. Чем выше частота дискретизации и чем больше количество разных значений, которыми можно характеризовать сигнал, тем выше качество отображения звука.
В современных компьютерах обычно применяется частота дискретизации в 22 кГц или 44,1 кГц (1 кГц — это тысяча измерений за 1 секунду), а для представления значения сигнала выделяются 2 байта (16 бит), что позволяет различать 2 16 , то есть 65 536 значений.
Читайте также:


