На швейной фабрике мастер сшил одинаковые пальто
Числа от 1 до 100
Умножение и деление
Порядок выполнения действий
Ответы к стр. 27
1. Вспомни, в каком порядке надо выполнять действия (с. 24). Определи порядок выполнения действий в следующих выражениях и вычисли их значения.
18 : (11 - 5) + 47 2 • 9 - 6 • 3 24 : 3 + 9 – 3
2 1 3
18 : (11 - 5) + 47 = 18 : 6 + 47 = 3 + 47 = 50
1 3 2
2 • 9 - 6 • 3 = 18 - 6 • 3 = 18 - 18 = 0
2 1 3
24 : 3 + 9 - 3 = 8 + 9 - 3 = 17 - 3 = 14
2. Составь выражения по схемам; определи в них порядок действий и вычисли их значения.
[] - [] + [] [] - [] : [] [] - ([] + []) : []
[] : [] • [] [] + [] • [] [] + [] • ([] - [])
[] - [] • [] [] + [] : [] [] • ([] + []) + []
72 - 53 + 12 = 19 + 12 = 31
21 : 3 • 5 = 7 • 5 = 35
56 - 12 • 3 = 56 - 36 = 20
43 - 18 : 3 = 43 - 6 = 27
35 + 13 • 4 = 35 + 52 = 87
63 + 24 : 8 = 63 + 3 = 66
95 - (44 + 76) : 4 = 95 - 120 : 4 = 95 - 30 = 65
81 + 2 • (46 - 34) = 81 + 2 • 12 = 81 + 24 = 105
14 • (2 + 3) + 18 = 14 • 5 + 18 = 70 + 18 = 88
3. Составь по таблице три задачи и реши их.
| Расход ткани на один костюм | Количество костюмов | Расход ткани на все костюмы |
| 3 м | 2 шт. | ? |
| ? | 2 шт. | 6 м |
| 3 м | ? | 6 м |
1) На изготовление одного костюма расходуется 3 м ткани. Сколько метров ткани потребуется для изготовления двух таких костюмов?
3 • 2 = 6 (м) - ткани на два костюма
О т в е т: на два костюма потребуется 6 м ткани.
2) На изготовление двух одинаковых костюмов потратили 6 м ткани. Сколько метров ткани пошло на один костюм?
6 : 2 = 3 (м) - ткани на один костюм
О т в е т: на один костюм пошло 3 м ткани.
3) На изготовление одного костюма требуется 3 м ткани. Сколько таких костюмов можно изготовить из 6 м ткани?
6 : 2 = 3 (шт.) - костюмов
О т в е т: можно изготовить 3 костюма.
4. Сшили 4 плаща, расходуя на каждый по 3 м ткани.
Поставь вопрос и реши задачу. Составь и реши две задачи, обратные данной.
Сколько всего метров ткани потратили на изготовление плащей?
3 • 4 = 12 (м) - ткани потратили всего
О т в е т: всего потратили 12 м ткани.
1) Из 12 м ткани изготовили 4 одинаковых плаща. Сколько метров ткани пошло на один плащ?
12 : 4 = 3 (м) - ткани пошло на один плащ
О т в е т: на один плащ пошло 3 м ткани.
2) На изготовление одного плаща требуется 3 м ткани. Сколько таких плащей можно изготовить из 12 м ткани?
12 : 3 = 4 (шт.) - плащей
О т в е т: можно изготовить 4 плаща.
5. Какая фигура лишняя? Найди разные решения.
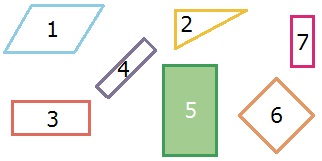
1) Лишняя фигура 2 - треугольник, так как все остальные фигуры четырёхугольники.
2) Лишняя фигура 5 - закрашенный четырёхугольник, так как все остальные фигуры не закрашены.
3) Лишняя фигура 1 - параллелограмм, так как у всех остальных фигур есть хотя бы один прямой угол.
7 • 3 - (16 + 4) 12 : (3 • 2) - 2 18 : 9 + 27 : 3
7 • 3 - (16 + 4) = 7 • 3 - 20 = 21 - 20 = 1
12 : (3 • 2) - 2 = 12 : 6 - 2 = 2 - 2 = 0
18 : 9 + 27 : 3 = 2 + 27 : 3 = 2 + 9 = 11
Задание на полях
К 1 прибавили 5 - получили 6, к 6 прибавили 6 (5 + 1) - получили 12, к 12 прибавили 7 (6 + 1) и так далее, то есть каждый раз прибавляется число на 1 больше того, которое прибавили. Следующие числа 36 + 10 = 46 и 46 + 11 = 57.
Формировать умение понимать взаимосвязи между данными и искомыми задачи для нахождения новых способов решения.
Чтобы достичь этой цели сформулируем задачи, которые требуют решения:
- научить вычленять компоненты или составные части задачи;
- научить видеть взаимосвязи между данными и искомыми;
- создать условия для открытия способа фиксации этих отношений (числовая прямая, схема, формула, таблица, чертеж);
- поиск плана решения задачи;
- выполнение плана;
- проверка, выбор приема нахождения другого способа решения задачи.
Ожидаемый результат решения поставленных задач будет следующим: дети будут видеть различные подходы к решению задач.
Одна из основных задач современной школы состоит в том , чтобы помочь учащимся в полной мере проявить свои способности , развить инициативу , самостоятельность , творческий потенциал .
Успешная реализация этих задач во многом зависит от форсированности у учащихся познавательных интересов , которые возникают тогда , когда школьники имеют возможность включиться в выполнение таких видов заданий , в которых они могут достичь успеха и вместе с тем чувствуют необходимость преодоления определенных препятствий при достижении цели .
Привитие интереса к учению является важным средством повышения качества обучения школьников . Большие возможности для развития интереса учащихся к математике имеют задачи . Процесс
Решения задач является наиболее эффективным средством развития гибкости мышления . Наибольший эффект при этом может быть достигнут в результате применения различных форм работы над задачей . Поэтому полезно организовать решение задач поиски других способов, запись этих способов, сравнение их с предыдущими, выбор лучшего варианта решения.
Умения ученика увидеть возможности решения задачи разными способами характеризует степень осознания им ситуации данной в задаче, понимание взаимосвязи между данными и искомыми, его наблюдательность, математическую зоркость, математический язык.
Рассмотрим несколько приемов помогающих видеть различные подходы к решению задач.
- 1 .Построение иной модели задачи, чем та, которая была использована при решения задачи первым способом.
- Использование другого способа разбора задачи при составлении плана решения.
- Дополнение условием задачи сведениями не влияющими на результат решения.
- Представление практического разрешения ситуации, описанной в задачи.
- Изменение формулировки текста задачи.
Остановимся на приемах нахождения различных способов решения текстовых задач.
1. Построение иной модели задачи, чем та, которая была использована при решении задачи первым способом.
В районных соревнованиях принимали участие 18 пловцов из нашей школы, а из соседней школы в 2 раза больше пловцов. Сколько всего пловцов участвовало в соревнованиях из 2-х школ?
Традиционное решение выглядит таким образом.
- 18*2=36(пл) - из соседней школы;
- 18+36=54(пл)
Ответ: 54 пловца.
Строим чертеж к задаче.
В результате анализа чертежа дети приходят к выводу, что решения этой задачи может быть найдено с помощью выполнения одного действия, т.к. 18*3 = 54 (пл).
При решении задач, содержащих пропорциональную зависимость, помогает найти схематический рисунок.
В магазин привезли 12ящиков с яблоками, по 8кг в каждом. До обеденного перерыва было продано 9 ящиков. Сколько килограммов яблок осталось продать после обеденного перерыва?
1 Способ (путем рассуждений от вопроса к данным)
- 8 * 12 = 96(кг) - яблок привезли в магазин;
- 8 * 9= 72(кг) - продали до обеда;
- 96 - 72 = 24(кг) - осталось продать.
По рисунку видно, что после обеда осталось продать 3 ящика яблок, по 8 кг в каждом, где (12-9 = 3).
- 12 — 9 = 3(ящ) - осталось продать;
- 8 * 3 = 24 (кг) - осталось продать.
Ответ: 24 кг яблок.
При решении некоторых задач хорошим подспорьем в отыскивании других способов решения является табличная форма краткой записи и поиск плана решения по таблице.
Утром ушли в море 20 маленьких и 8больших рыбацких лодок, 6 лодок вернулись. Сколько лодок с рыбаками должны еще вернуться?
Цель: развитие математического мышления и творческой активности учащихся.
Задача: воспитать у учащихся навыки самостоятельного поиска решения задачи.
Решение задач имеет большое образовательное и воспитательное значение. Оно способствует умственному развитию детей и в особенности развитию логического мышления, так как в процессе решения задач ребята учатся рассуждать и обосновывать свои суждения. Решение задач оказывает огромное влияние на развитие самостоятельности мышления, речи, воображения, внимания и памяти учащихся, на воспитание у них воли, активности и инициативы. В процессе решения задач школьники приобретают навык работы по плану, экономно выбирать средства для достижения цели, обосновывать и анализировать свои действия. Поэтому работа над задачей остаётся одним из важнейших аспектов обучения в начальной школе, когда закладываются основы знаний; является движущим фактором в общем развитии младших школьников.
В ходе моей многолетней работы в школе замечено, что дети часто испытывают затруднения в решении текстовых задач. Пришла к выводу, что использование однотипных приемов работы над задачей снижает интерес к ним. Было бы лучше, чтобы дети думали и рассуждали, решая задачи, а не узнавали в каждой ту, которую решали раньше.
Пытаясь снять эту проблему, решила разнообразить деятельность учащихся при решении задач.
- задачи с недостающими или лишними данными;
- сопоставление задач;
- составление обратных задач;
- решение задач несколькими способами;
- задачи, в которых предлагается изменить условие или вопрос задачи так, чтобы увеличилось или уменьшилось количество действий;
- составление задачи по рисунку или данному выражению;
- задачи, связанные с геометрией;
Такой подход к решению задач оживил работу, у детей стала развиваться самостоятельность, мыслительная деятельность.
Работа над задачей начинается с первого класса. Дети по рисунку составляют математические рассказы или иллюстрируют данные в задаче с помощью картинок. На этом этапе у учащихся раскрывается смысл арифметических действий сложения и вычитания, они учатся выражать последовательность мыслей. При составлении задач школьники рассуждают над своей работой, им предоставлена свобода, и они, составляя задачи, творят, самостоятельно применяют определенные знания и умения. Составляя задачи, дети сталкиваются с трудностями, преодоление которых вызывает активную мыслительную деятельность.
Работа по составлению задач ведется на протяжении всего периода обучения в начальных классах с постепенным усложнением. В зависимости от сложности и объема работы на ее выполнение отводится 3-10 минут.
С 1-го класса дети учатся отличать задачу от обыкновенного текста, выделять ее элементы: условие, вопрос, данные, искомые, осознавать их взаимосвязь. Ребенок должен научиться читать задачу, понимать смысл прочитанного, пересказывать содержание, подмечать какие события произошли в задаче, правильно выбирать решение задачи.
Но как же научить ребенка осмысленно знакомиться с текстом задачи, ведь некоторые дети читают задачу поверхностно, не вдумываясь в содержание задачи?
Исследуя условие и вопрос задачи, ученик видит, что небольшое изменение меняет способ решения, ответ и возможность вычисления. У учащихся воспитывается диалектное мышление.
Например, предлагаются задачи:
На изменение вопроса.
Для утренника купили 4 кг конфет по 80 р. и 3 кг печенья. За всю покупку заплатили 380 р. Сколько стоит 1 кг печенья.
1) 80 * 4 = 320 (р.) – заплатили за конфеты;
2) 380 – 320 = 60 (р.) – стоят 3 кг печенья;
3) 60 : 3 = 20 (р.) – стоит 1 кг печенья;
Измени вопрос задачи так, чтобы количество действий уменьшилось. Какие можно задать вопросы?
(Сколько стоят 3 кг печенья? Сколько стоят конфеты?)
1) Друзья утром съели 5 яблок, а днём – ещё 3. Сколько всего они съели яблок?
2) Друзья утром съели 5 яблок, а днём – ещё 3. На сколько больше они съели яблок утром, чем днём?
Прочитай тексты и докажи, что это задачи.
Чем задачи похожи? Чем различаются? Как ты думаешь, решения этих задач будут одинаковыми? Объясни ответ.
Реши задачи и объясни выбор действий.
Придумай свою задачу, которую нужно решать тем же действием, что и первую задачу из данных.
Измени вопрос своей задачи так, чтобы её решение стало таким же, как у второй задачи.
На составление обратных задач.
1) На клумбе распустилось 28 роз. 11 из них срезали для букета. Сколько роз осталось на клумбе?
2) Когда для букета срезали 11 роз, на клумбе осталось ещё 17. Сколько роз было на клумбе сначала?
Сравни решения задач. Какая между ними связь? От чего она зависит?
Как бы ты назвал эти задачи? Почему?
Какую ещё задачу, обратную данным, можно составить? Запиши такую задачу и её решение.
Вышеуказанные виды задач обеспечивают одновременное осмысленное усвоение противоположных понятий и помогают детям различать близкие и сходные между собой понятия.
Одним из эффективных приёмов мышления учащихся, включений их в творческую деятельность, является поиск различных способов решения задачи.
На пошив 8 одинаковых пальто израсходовали 24 м ткани. Сколько метров ткани потребуется на 2 таких же пальто?
1) 24 : 8 = 3 (м) – ткани требуется для одного пальто;
2) 3 * 2 = 6 (м) – ткани потребуется на 2 пальто.
1) 8 : 2 = 4 (раза) – меньше изготовят пальто;
2) 24 : 4 = 6 (м) – ткани потребуется на 2 пальто;
Изменим частично условие и вопрос задачи, решим новую задачу.
На швейной фабрике мастер сшил одинаковое пальто, израсходовав на них 24 метра ткани. Его ученица сшила 2 таких же пальто и израсходовала на них 6 м ткани. Сколько всего пальто сшили мастер и ученица?
1) 6 : 2 = 3 (м) – ткани требуется на одно пальто;
2) 24 : 3 = 8 (п.) – сшил мастер;
3) 8 + 2 = 10 (п.) – сшили мастер и ученица вместе;
1) 6 : 2 = 3 (м) – ткани требуется на одно пальто;
2) 24 + 6 = 30 (м) – ткани всего израсходовали мастер и ученица;
3) 30 : 3 = 10 (п.) – сшили мастер и ученица;
1) 24 : 6 = 4 (раза) – больше ткани потратил мастер;
2) 2 * 4 = 8 (п.) – сшил мастер;
3) 8 + 2 = 10 (п.) – сшили мастер и ученица;
Таким образом, учащиеся видят различные способы выполнения вычислений и выбирают рациональный, что способствует формированию гибкости и рациональности мышления.
Детям очень нравится решать задачи с недостающими или лишними данными.
На ферме живут 20 коров, а овец на 12 меньше, чем свиней. Сколько домашних животных на ферме?
Прочитай задачу. В чём её особенность?
Можно ли ответить на вопрос задачи? Почему?
Дополни условие задачи так, чтобы её можно было решить, и запиши решение.
Не добавляя данных, попробуй изменить условие задачи так, чтобы её тоже стало возможно решить.
Запиши решение новой задачи.
Из 48 метров ткани сшили 6 платьев, 4 блузки и 4 халата. На все блузки пошло 8 м ткани, на платья на 16 м больше, чем на блузки. Сколько ткани пошло на халаты?
Сравни условие задачи и её решение. Все ли данные ты использовал для получения ответа на вопрос задачи?
Измени условие задачи так, чтобы в нём остались только нужные для решения числа.
Какие данные станут в них лишними, если поставить такой вопрос: Сколько метров ткани пошло на платье и сколько на халат?
Реши получившуюся задачу.
Поставь к условию задачи такой вопрос, чтобы для ответа на него потребовались все данные.
Запиши его и реши задачу.
Детей привлекает работа, связанная с решением геометрических задач.

На участке прямоугольной формы длиной 12 м и шириной 8 м построили дом. Размеры дома показаны на рисунке. Чему равна свободная площадь двора?
Работая таким образом над решением задач, пришла к выводу, что целесообразно привлекать детей к решению разнообразных задач повышенной трудности, добиваясь того, чтобы сам процесс поиска решений и полученный ответ задачи приносил радость ученику. В классе следует создавать атмосферу заинтересованности, развивать у них чувство достоинства, самоуважения.
С повышенным интересом и большой активностью дети решают задачи связанные с жизненными ситуациями самих детей. Для этого включаю в учебный процесс задачи занимательного характера, задачи на логическое мышление. (Приложение)
Всё это активизирует мыслительную деятельность и формирует интеллектуальные умения.
С первого класса мною ведётся отслеживание за умением решать задачи детьми.
На каждого ребёнка заведена индивидуальная карта, где я отмечаю успехи учащихся в решении задач. Это мне помогает в индивидуальной работе со слабоуспевающими учениками, в дифференцированном подходе к обучению каждого ребёнка.
Результатом моей работы можно считать повышение качества решения задач, стабильные высокие результаты контрольных работ и математических срезов знаний. Для заинтересованности детей подобраны разные виды задач, помогающие мне в системе работать над повышением качества решения задач, развитием математического мышления и творческой активности учащихся на уроках математики.

В презентации коротко описаны разные приемы и способы решения задач в начальной школе.
Просмотр содержимого документа
«Презентация "Способы решения задач"»

Учителя начальных классов


Виды задач, изучаемые в 3 классе:
- на увеличение и уменьшение числа в несколько раз;
- на кратное сравнение;
- на увеличение и уменьшение числа в несколько раз (в косвенной форме);
- на привидение к единице;
- на нахождение суммы двух произведений;
- на нахождение неизвестного слагаемого;
- на цену, количество, стоимость;
- на нахождение числа по доле и доли по числу;
- на нахождение площади;
- составные задачи на деление суммы на число и числа на сумму.
"Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?"
Способы решения задачи:
практический или предметный :
арифметический:
алгебраический :
Число тарелок неизвестно, обозначим их буквой х . На каждой тарелке 2 яблока, значит, число всех яблок - это
2 ∙ х. Так как в условии известно, что число всех яблок 8, то можно записать уравнение 2 ∙ х = 8 и решить его:
х = 8 : 2, х = 4.
графический:


"Для уроков труда купили 4 катушки белых ниток, по 6руб. за катушку, и 6 катушек чёрных ниток по такой же цене. Сколько денег уплатили за эти нитки?"
Формы записи решения задачи:
по действиям с планом:
1 способ:
6 ∙ 4 = 24 ( р)
2) Сколько стоят чёрные нитки?
3) Сколько стоят все нитки?
24 + 36 = 60 (р)
2 способ:
4 + 6 = 10 ( к.)
2) Сколько стоят все нитки?
6 ∙ 10 = 60 (р)
Ответ: 60 рублей.

по действиям с пояснением:
1 способ:
2) 6 ∙ 6 = 36 (р) – стоят чёрные нитки;
3) 24 + 36 = 60 (р) – стоят все нитки.
2 способ:
2) 6 ∙ 10 = 60 (р) - стоят все нитки.
Ответ: 60 рублей.
по действиям без пояснений:
1 способ:
2) 6 ∙ 6 = 36 (р)
3) 24 + 36 = 60 (р)
2 способ:
2) 6 ∙ 10 = 60 (р)
Ответ: 60 рублей стоят все нитки.

составить выражение:
4 ∙ 6 + 6 ∙ 10 = 60 (р)
Ответ: 60 рублей стоят все нитки.

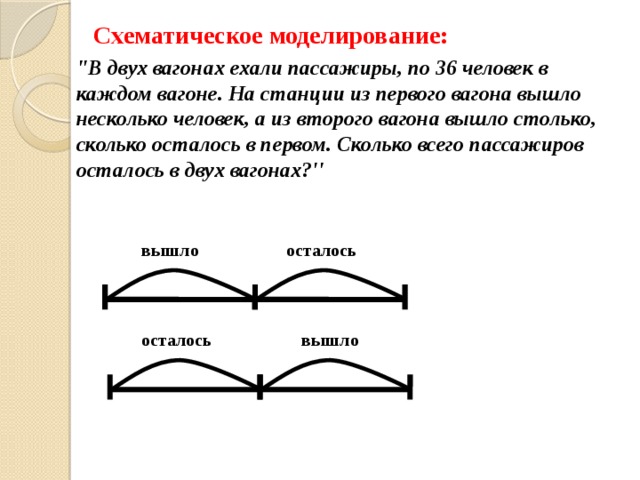
Схематическое моделирование:
"В двух вагонах ехали пассажиры, по 36 человек в каждом вагоне. На станции из первого вагона вышло несколько человек, а из второго вагона вышло столько, сколько осталось в первом. Сколько всего пассажиров осталось в двух вагонах?''

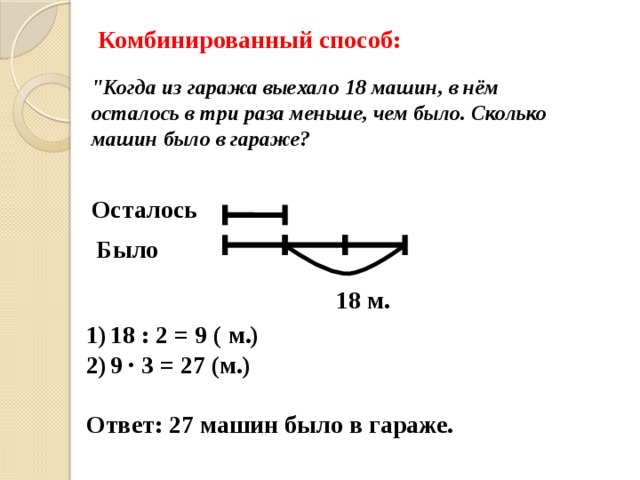
Комбинированный способ:
"Когда из гаража выехало 18 машин, в нём осталось в три раза меньше, чем было. Сколько машин было в гараже?
Ответ: 27 машин было в гараже.
А В : А = Х : К 2 способ: Х= К ∙ ( В : А) " width="640"
«На пошив А одинаковых изделий израсходовано К м ткани. Сколько ткани потребуется на пошив В таких же изделий?
1 способ:
Х= ( К : А ) ∙ В
2 способ:

«На пошив 8 одинаковых пальто израсходовали 24 м ткани. Сколько ткани потребуется на 2 таких же пальто?
Кол-во пальто
Общий расход ткани. м

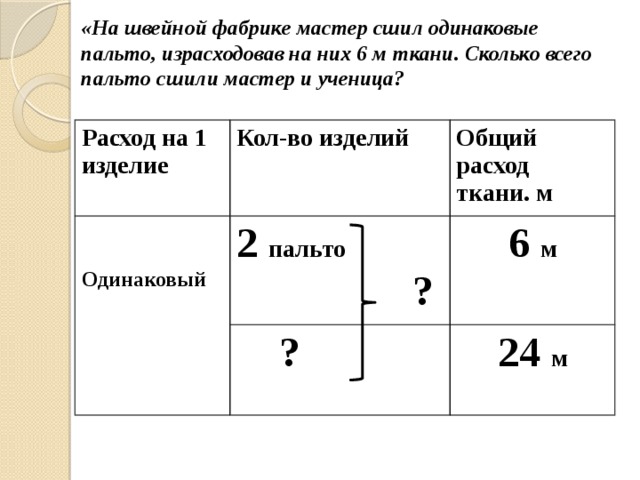
«На пошив 8 одинаковых пальто израсходовали 24 м ткани. Сколько ткани потребуется на 2 таких же пальто?»
Расход на 1 изделие
Кол-во пальто
Общий расход ткани. м
2 пальто
8 пальто

1 способ:
2) 2 ∙ 3 = 6 ( м) – на 2 пальто.
2 способ:
- 8 : 2 = 4 - изделий в 4 раза меньше, поэтому и ткани израсходовали меньше в 4 раза;
2) 24 : 4 = 6 (м) – в 4 раза меньше, чем 24 м.
«На швейной фабрике мастер сшил одинаковые пальто, израсходовав на них 6 м ткани. Сколько всего пальто сшили мастер и ученица?
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Столичный центр образовательных технологий г. Москва
Получите квалификацию учитель математики за 2 месяца
от 3 170 руб. 1900 руб.
Количество часов 300 ч. / 600 ч.
Успеть записаться со скидкой
Форма обучения дистанционная
Практическая работа №4
«Методика решения задач по математике в начальной школе»
1. Составить тексты задач на пропорциональную зависимость (3 группы – всего 12 видов), используя тройку величин:
• расход ткани на 1 вещь;
• общий расход ткани.
2. Используя содержание задачи: «В одной коробке было 12 карандашей. Сколько карандашей было в 3-х таких же коробках?», проиллюстрируйте вариант работы по формированию представлений о пропорциональной зависимости между величинами, используя для этого приемы:
• изменение одного из данных задачи;
• сравнение результатов решения задач, в которых изменяется одно из данных; • моделирование задачи в виде схемы, таблицы.
3. В чем особенность следующих текстов задач? С какой целью и как образом их можно использовать при работе с задачами на пропорциональную зависимость?
• Коля купил 3 ручки и 2 фломастера. За что он заплатил денег больше, за ручки или фломастеры?
• В столовую завезли 8 ящиков с абрикосами и 10 ящиков с виноградом? Масса каких фруктов была больше?
4. Определите цель сравнения каждой пары задач. Какие виды задач сравниваются?
На пошив 8 одинаковых пальто израсходовано 24 м ткани. Сколько ткани потребуется на 2 таких же пальто?
На пошив 8 одинаковых пальто израсходовано 24 м ткани. Сколько ткани потребуется на 6 таких же пальто?
На пошив 8 одинаковых пальто израсходовано 24 м ткани. Сколько ткани потребуется на пошив 2-х таких же пальто?
Мастер сшил 8 одинаковых пальто, а его ученица 2 таких же пальто. Сколько ткани израсходовал каждый из них, если мастер потратил на 24 м ткани больше?
Мастер сшил 8 одинаковых пальто, а его ученица 2 таких же пальто. Сколько ткани израсходовал каждый из них, если мастер потратил на 30 м ткани больше?
Мастер сшил 8 одинаковых пальто, а его ученица 2 таких же пальто. Вместе они израсходовали 30 м ткани. Сколько ткани израсходовал каждый из них?
Масса 8 одинаковых ящиков с фруктами равна 24 кг. Какова масса 2-х таких ящиков с фруктами?
На пошив 8 одинаковых пальто израсходовано 24 м ткани. Сколько ткани потребуется на пошив 2-х таких же пальто?
Подберите или составьте задачи, которые можно предложить обучающимся для сравнения с этими же целями.
5. Спланируйте работу по формированию у младших школьников общих умений при решении следующих задач:
• За 7 дней в столовой израсходовали 21 кг масла. На сколько дней при той же норме хватит 36 кг масла?
• Две школы получили 100 одинаковых пачек учебников. Одна школа получила 600 экземпляров учебников, а другая 400 учебников. Сколько пачек учебников получила каждая школа?
• В мастерской из двух кусков материи сшили одинаковые палатки для туристов. В первом куске было 84 м материи, а во втором 60 м. Сколько палаток сшили из каждого куска, если известно, что из второго куска сшили на 2 палатки меньше?
6. Прочитайте задачу. Решите ее разными арифметическими способами. На швейной фабрике мастер сшил одинаковые пальто израсходовав на них 24 м ткани. Его ученица сшила 2 таких же пальто и израсходовала на них 6 м ткани. Сколько всего пальто сшили мастер и ученица?
• Спланируйте фрагмент организации деятельности обучающихся в процессе работы над данной задачей, используя приемы: изменение условия и вопроса; поиск разных способов решения (в том числе при помощи схемы).
• Составьте все возможные вопросы, на которые можно ответить, пользуясь условием данной задачи.
7. Разработайте фрагменты урока по формированию у младших школьников общих умений при работе с задачами на пропорциональное деление и нахождение четвертого пропорционального.
8. Охарактеризуйте виды движения, изучаемые в начальной школе, а также основные понятия, связанные с движением тел.
9. Выпишите типы упражнений, которые можно использовать на подготовительном этапе для формирования представлений о «времени» и «расстоянии». Определите их цели. Какие модели для этого предлагаются в различных учебниках математики для начальной школы?
10. Определите цели сравнения предложенных пар задач: а)
Килограмм конфет стоит 12руб., а килограмм печенья в 2 раза меньше. Сколько стоит 1 кг печенья?
Лыжник проходит за 1 час 12 км, а пешеход в 2 раза меньше. Сколько километров пешеход проходит за 1 час?
В трех коробках 15 кг печенья. Сколько печенья в одной коробке?
За 3 часа пешеход прошел 15км. Сколько километров он пройдет за 1 час?
Каким образом их можно использовать на подготовительном этапе?
11. Одним из эффективных приемов формирования представлений о скорости движения и взаимосвязи между величинами является прием решения задач с недостающими данными. Проиллюстрируйте данный прием, используя текст задачи: «Один велосипедист едет до города 15 мин, а другой – 25мин. Кто едет быстрее, а кто медленнее?»
12. Для успешного решения задач, связанных с движением тел, обучающимся необходимо уметь заменять крупные единицы каждой из трех величин (скорость, время, расстояние) мелкими, и наоборот. Соответствуют ли данной цели предложенные упражнения?
• Объясни следующие выражения: «Скорость самолета 70км/ч», «Пешеход проходит 5 км за 1 час».
• Сравни скорости: 5км/ч…500м/мин 300км/ч…5км/мин
• Реши задачу: «Скорость одного пешехода 50 м/мин, а другого – 4 км/ч. За какое время первый пешеход пройдет 12 км? За какое время это расстояние пройдет второй пешеход?»
• Реши задачу: «Пешеход проходит за 1 час 5 км. Сколько метров он пройдет за 1 минуту?»
13. Решите задачу всеми арифметическими способами. «Теплоход за 6 часов прошел 120км. Сколько километров он пройдет за 3 часа, если будет идти с той же скоростью?» Для подготовки к решению данной задачи разными способами учитель использовал задания:
• Пешеход проходит 1 км за 15 мин. Сколько километров он пройдет за 1 час? За 2 часа?
• За 3 часа пешеход проходит 12 км. Сколько километров он пройдет за 1 час? Сколько минут потребуется для прохождения 1 км?
Зачем были предложены эти задания? Как помочь обучающимся найти все возможные способы решения? Какие модели для этого можно использовать? Можно ли решить первую задачу алгебраически и графически? Все ли данные необходимы для графического решения?
14. Особая роль в формировании у младших школьников общих умений решать задачи отводится задачам на движение в противоположных направлениях (на сближение и удаление). Сравните задачи. Чем они похожи? Чем отличаются?
Из двух пунктов одновременно вышли два пешехода навстречу друг другу и встретились через 3 часа. Найти расстояние между пунктами, если скорость первого была 5 км/ч, а скорость второго 4 км/ч.
Из одного пункта одновременно вышли два пешехода и пошли в противоположных направлениях. Один из них шел со скоростью 5 км/ч, а другой 4 км/ч. На каком расстоянии они были через 3 часа?
Решите данные задачи. Сравните решения. • Можно ли предложить данное задание обучающимся? Если да, то с какой целью?
15. Какие модели помогают осознать обучающимся понятия «скорость сближения» и «скорость удаления»?
16. Составьте с величинами «скорость», «время», «расстояние» по одной задаче на нахождение четвертого пропорционального, на пропорциональное деление, на нахождение неизвестного по двум разностям.
Разработайте вариант организации деятельности обучающихся с каждой из задач.
17. Проиллюстрируйте различные варианты работы (2-3 методических приема, например, моделирование, решение разными методами и способами, сравнение и др.) по обучению решению задач, связанных с движением тел, на примере следующих задач:
• Расстояние между двумя городами в 360 км автобус проходит за 6 ч, а мотороллер за 12 ч. Через сколько часов произойдет встреча автобуса и мотороллера, если они одновременно выедут из этих городов навстречу друг другу?
• Из двух городов навстречу друг другу вышли одновременно два поезда и встретились через 18 часов. Определить скорость каждого поезда, если расстояние между городами 1620 км, а скорость одного поезда на 10км/ч больше скорости другого.
18. Проиллюстрируйте 3-4 методических приема, которые можно использовать на подготовительном этапе для формирования у обучающихся представлений о скорости, для овладения приемом моделирования и осознания зависимости между величинами в процессе решения простых задач, связанных с движением тел.
Читайте также:


