Как сшить параллелепипед
Как создать прямоугольник параллелепипед своими рукамиНаверняка многие из вас делали для разнообразных проектов подделки на тему геометрических фигур. Простейшей из моделей может стать самый обыкновенный параллелепипед, который мы часто видим в виде простой коробки.Для создания геометрических фигур нужно немного творческого воображения, доступные материалы и конечно же – шаблон, по которому будет сделана модель.

Что может понадобиться в работе?
Для начала следует определиться с набором материалов и для каких целей будет изготавливаться модель. Далее мы рассмотрим на конкретном примере как сделать параллелепипед из бумаги.

Для работы нужно подготовить:
- Клей,
- Бумагу,
- Картон,
- Ножницы,
- Ручку,
- Линейку,
- Карандаш.
- Модель параллелепипеда

Как сделать параллелепипед из бумаги схема
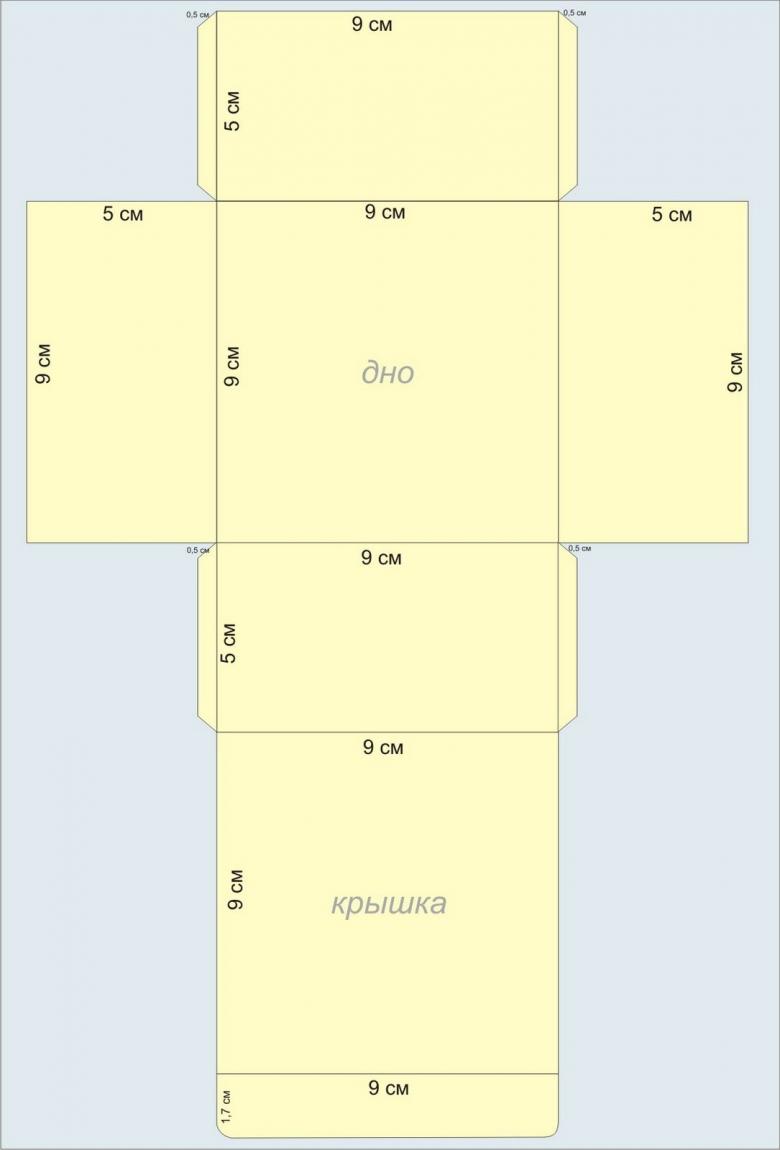
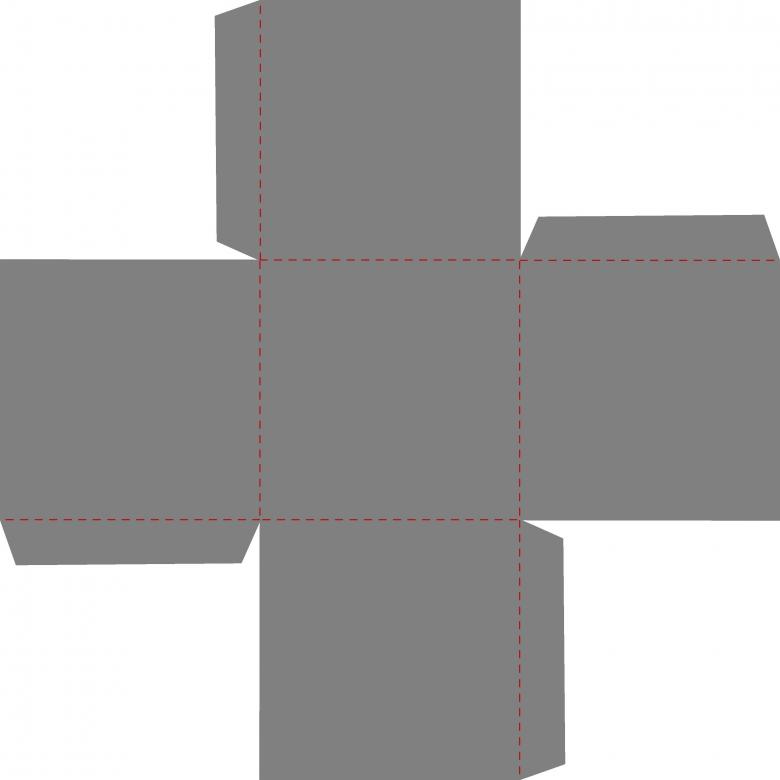
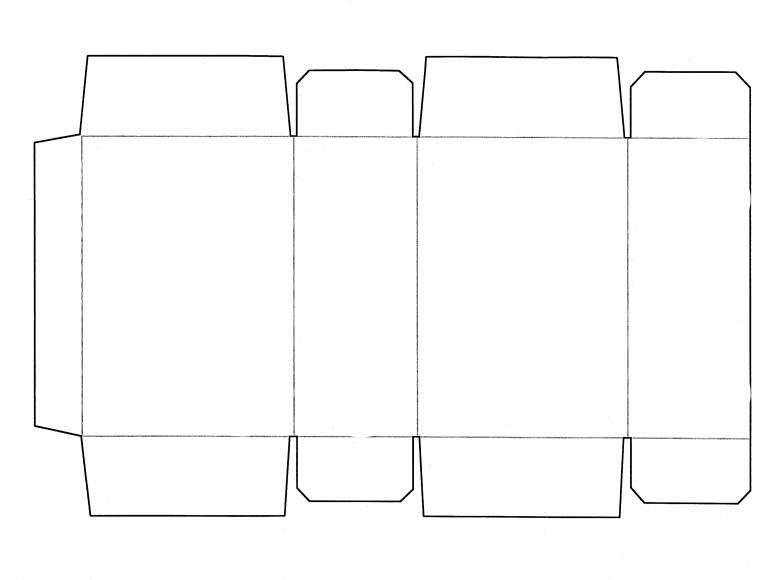
Для изготовления будет рассмотрена базовая модель. Как вы видите, шаблон полностью пропорционален своим сторонам и имеет контуры для загиба и склеивания модели по швам.
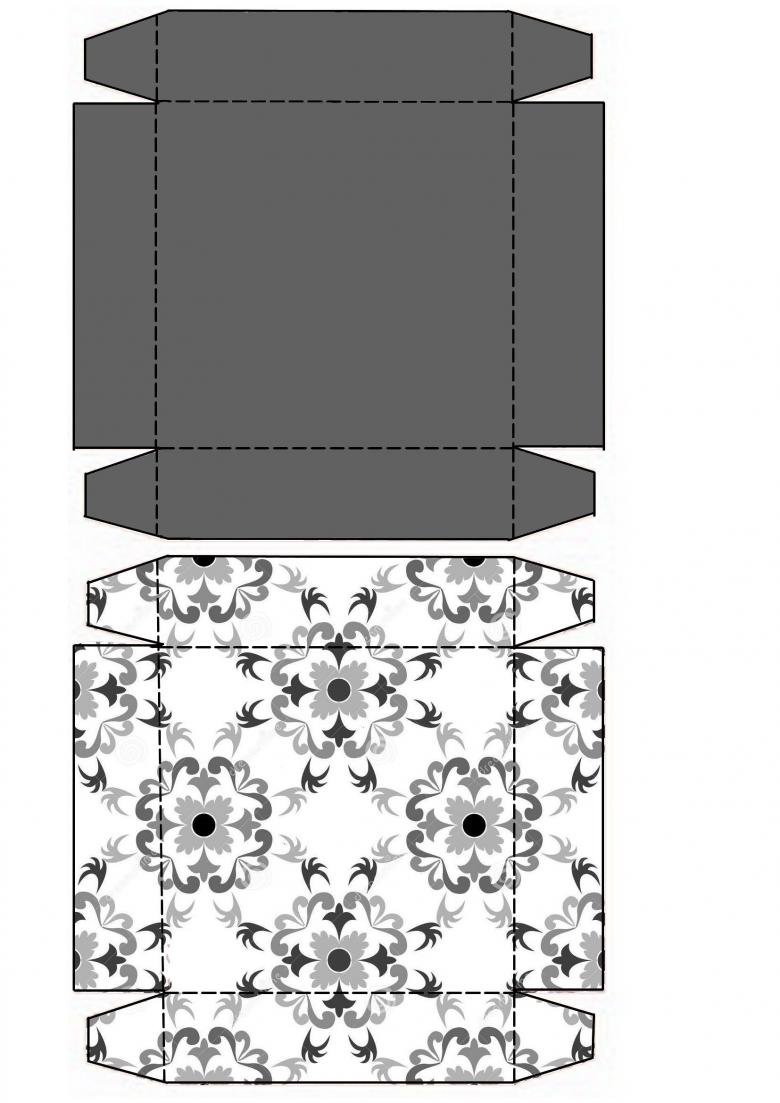
Если вам нужно изготовить параллелепипед большего размера, то для начала вам достаточно взять за основу одну центральную сторону, к которой идут «ушки» боковинок.

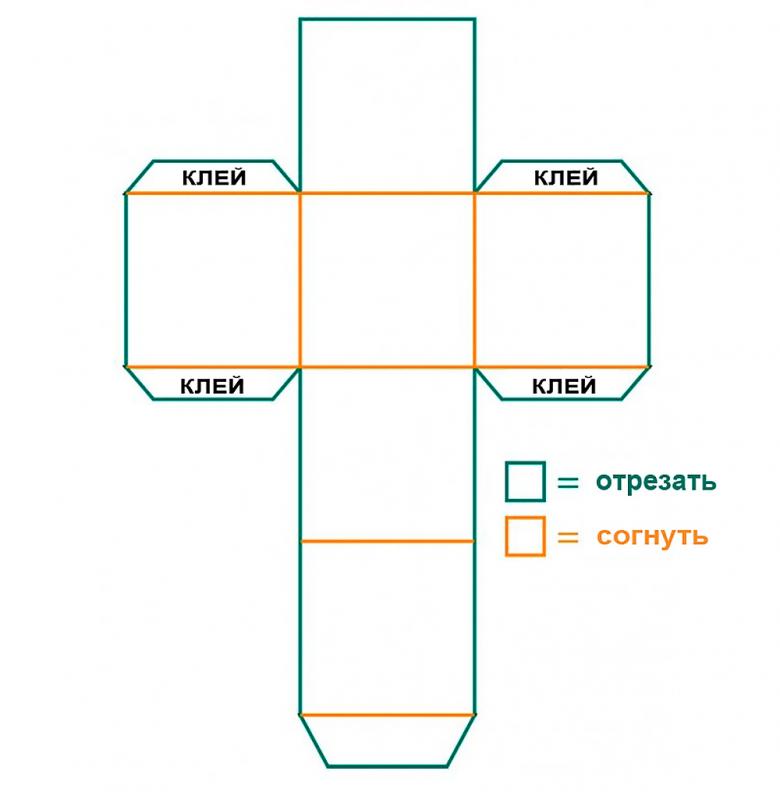
Основная сторона полностью пропорциональна своей стороне на параллели, а это значит, что соседние грани должны тоже быть параллельно пропорциональны друг другу. Чтобы не усложнять процесс, достаточно просто распечатать готовый шаблон и вырезать его по нужным линиям. Обратите внимание, что для уровня склейки боковые грани обозначены другим цветом.
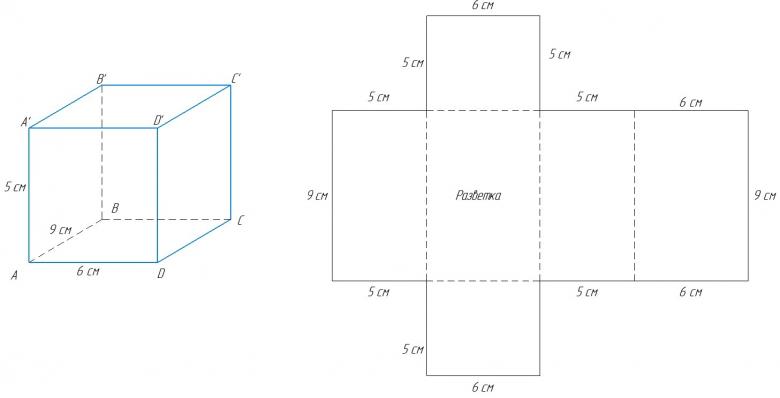
Важные моменты
Многие задаются вопросом, как сделать прямоугольный параллелепипед равномерным? В этом вопросе хорошо поможет карандаш и линейка, так как главное соблюдать пропорции размеров. Если их не будет, модель попросту не получиться, а если сделать все стороны одинаковыми, тогда у нас получиться не параллелепипед, а квадрат.

Где еще можно применить модель прямоугольника в быту и подделках?На одной только геометрии не сошелся мир, ведь в этом деле можно проявить фантазию, после чего простая и скучная модель превращается в настоящую красочную подделку.
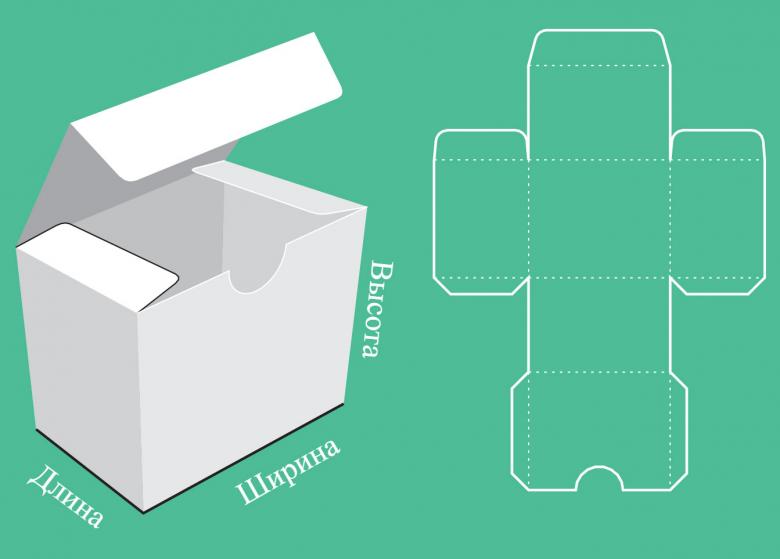
Идеи для творчества
Фотографии на прямоугольнике
Хотите добавить оригинальности собственным фотографиям? Тогда, почему бы их не сделать в рамку из параллелепипеда? Благодаря этой незамудренной модели вы сможете постоянно менять фотографии на любимой полке всего лишь перевернув вам прямоугольник на новую грань.

Что для изготовления понадобиться?
- Шаг 1 – Берем плотную бумагу или картон для изготовления модели.
- Шаг 2 – Наносим на картон шаблон параллелепипеда.
- Шаг 3 – Готовый шаблон следует наметить по расположению фотографий.
- Шаг 4 – Сделайте обрезку фотографий.
- Шаг 5 – Вырезайте готовый шаблон прямоугольника.
- Шаг 6 – Склейте модель за схемой по граням.
- Шаг 7 – После высыхания нанесите клей на грани.
- Шаг 8 – Приклейте поочередно фотографии с намеченным расположением.
- Шаг 9 – Дайте конструкции высохнуть.
- Шаг 10 – Все, модель готова к использованию.
По желанию можно покрыть модель прямоугольника скотчем, что обеспечит большую долговечность и сохранность.
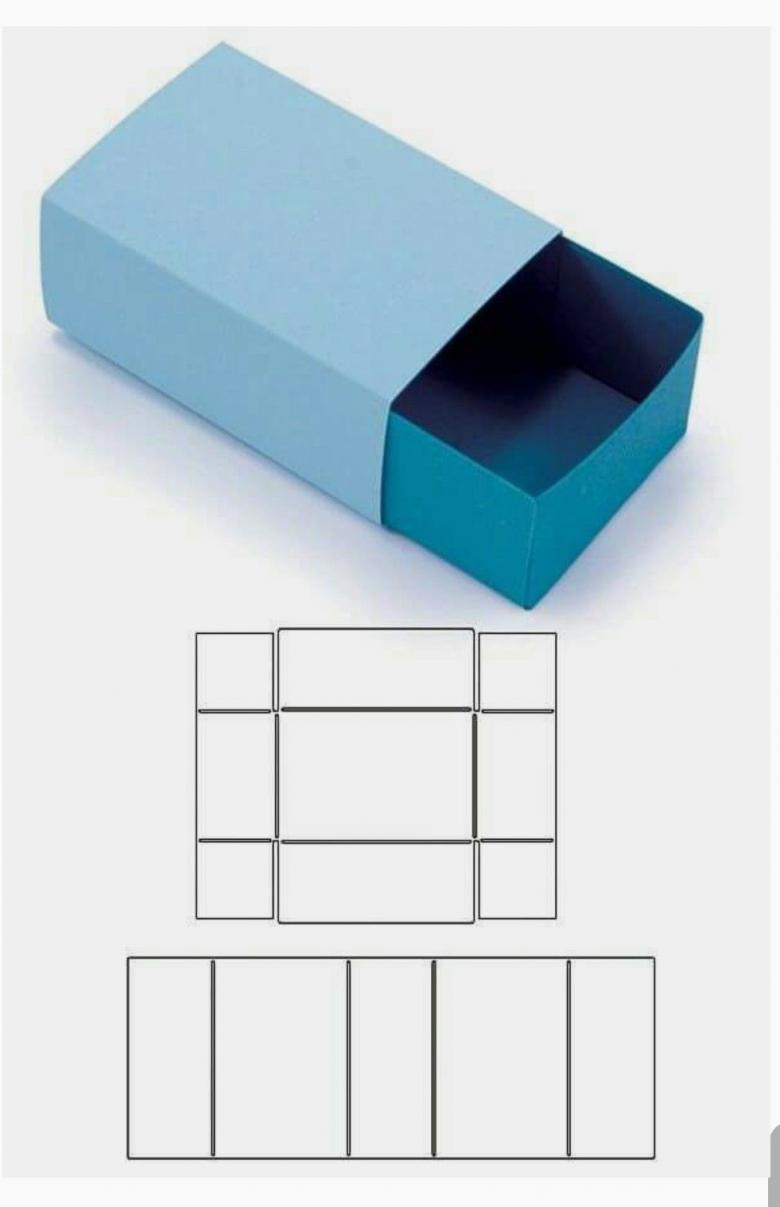
Коробочка на подарок
Сделать прямоугольную коробочку своими руками не так уж и сложно. Все что вам нужно, это придерживаться того же шаблона и пропорций. Единственное отличие, вам нужно не заклеивать плотно все стороны. Это нужно для того, чтобы готовую модель можно было использовать как коробку для подарка.

Процесс изготовления повторяем точно так же по шаблону, вырезая и сгибая в гранях, которые нуждаются в склеивание. Единственное, выберете сторону, которая будет играть роль «крышки» открывашки.После этого готовую коробочку можно украсить на любой лад и презентовать с подарком внутри, конфетами или какими-то пожеланиями.

Ромбический параллелепипед
Еще один оригинальный вариант создания прямоугольника может стать основа ромба. Кроме своей необычной формы этот вариант отлично подойдет на оформления подарка или какой-то подделки.Основная схема имеет в своей основе не прямоугольники, а ромбы, которые мы видим на готовой схеме.
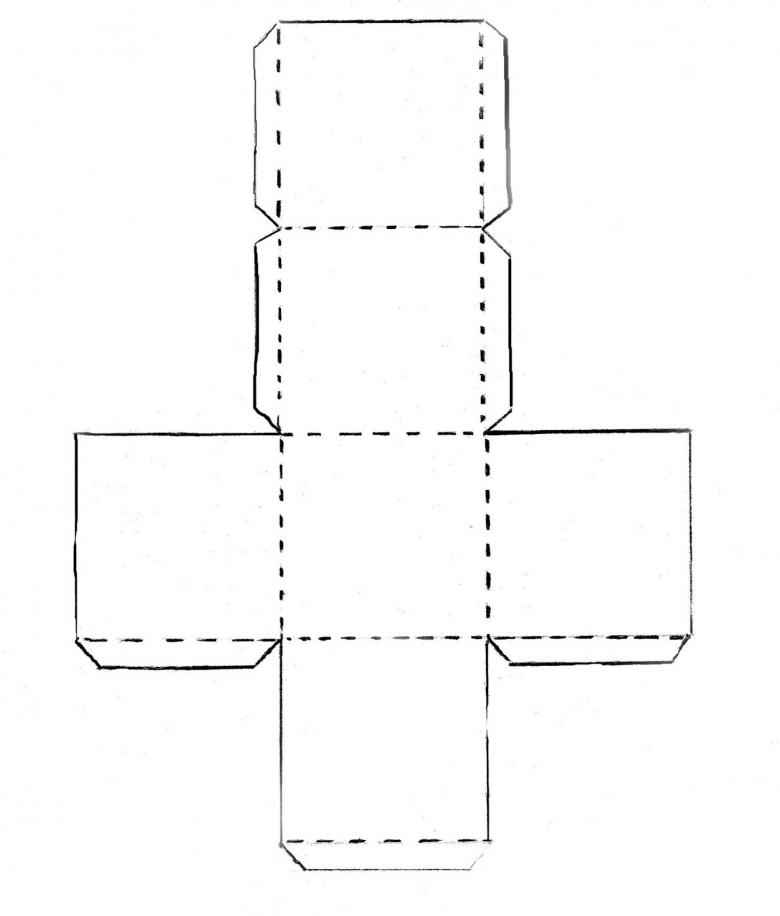
Для изготовления нанесите линейкой и карандашом первые два центральных ромба. Далее спускаетесь пропорционально «зеркально» вниз и вверх, тоже нанося на бумагу ромбы. Обратите внимание, что все стороны должны быть одинаковыми, иначе ромб получится неправильным.После этого достаточно нанести боковушку и «ушки» для склеивания.
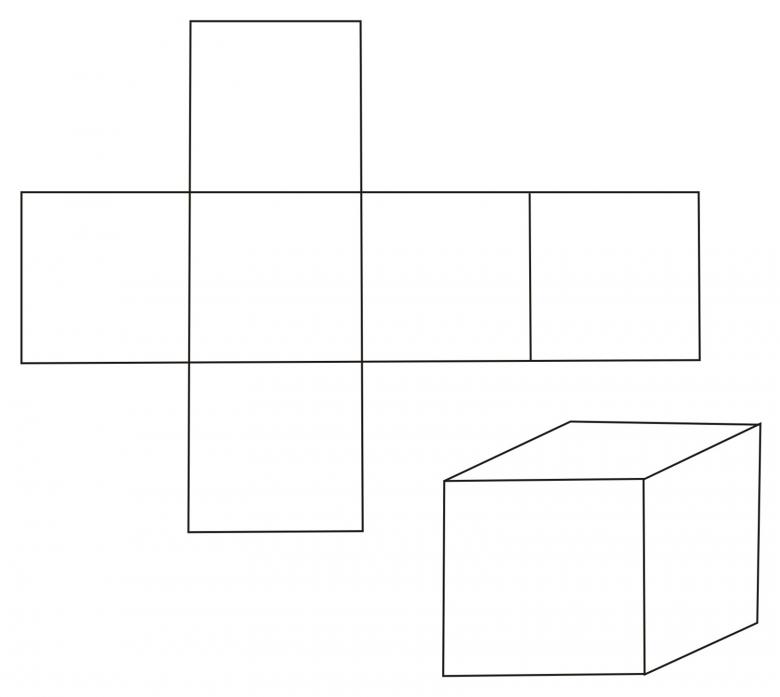
Кстати про «ушки» не обязательно делать их маленькими. Если они будут слишком маленькими вам трудно будет их склеить и сама модель получиться не такой плотной.
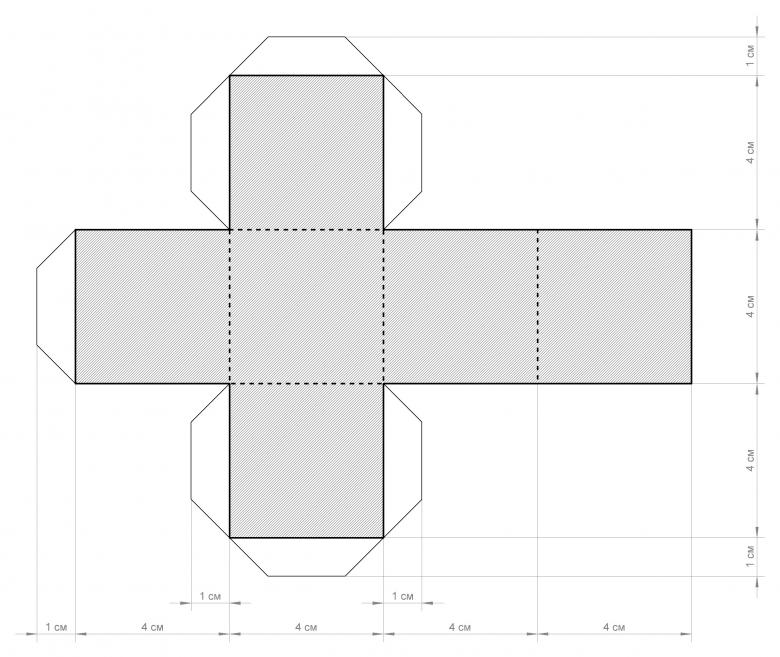
ВАЖНО! Не забывайте о технике безопасности работы с клеем, ножницами и другими материалами. Если вы готовите модель объемного параллелепипеда/прямоугольника, тогда рекомендуем вам проконсультировать детей в правильности использования материалов и инструментов, с которыми они работают. Объясните правила склейки и с какой стороны нужно загибать грани.
Параллелепипед школьникам
Довольно часто на уроках школьникам могут задавать создание разнообразных геометрических фигур, и прямоугольник – одна из них. Само по себе фигура является довольно простой, однако, многие испытывают трудности на этапе сборки модели.
Чтобы проблем не возникало, следует просто учитывать пропорции, и правильно загибать линии. В итоге работы должна получиться коробочка. Если вы испытываете трудности или модель не получается, возьмите готовую коробку (например из-под чая) и просто обклейте ее грани белой бумагой. Это придаст конструкции презентабельный вид и позволит быстро и ровно создать параллелепипед без особых усилий.
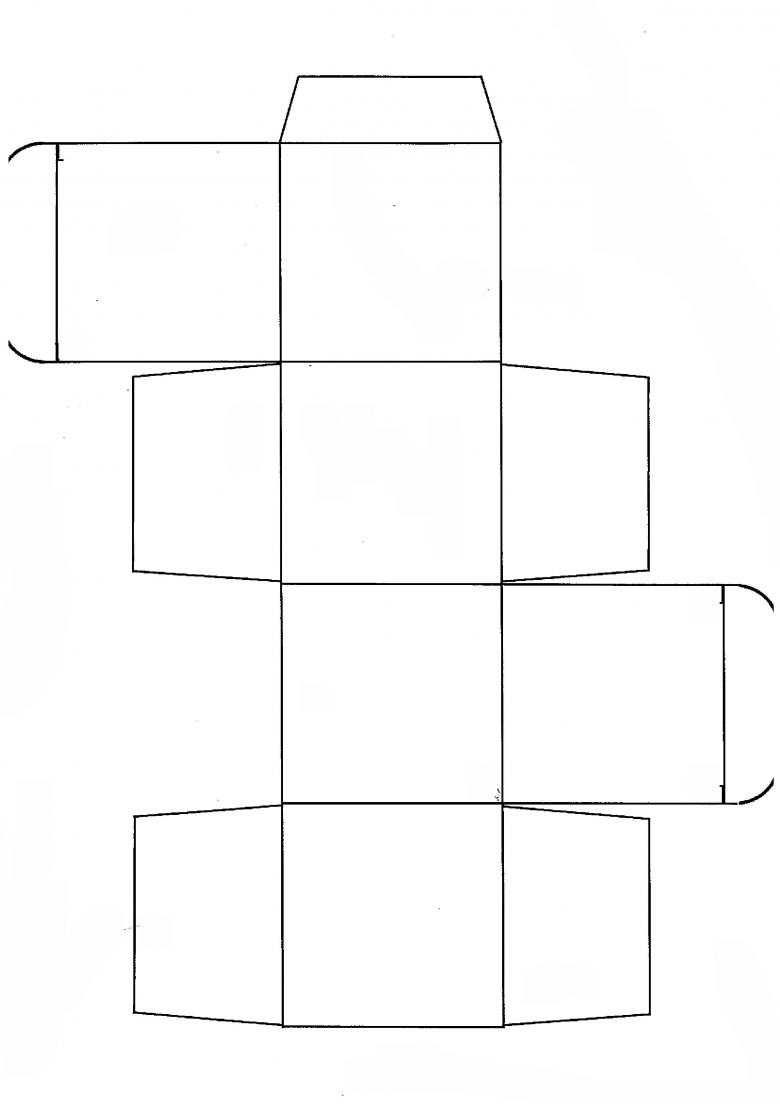
Для тех же, кто хочет целенаправленно сделать параллелепипед точно такой же формы, достаточно «разобрать» готовую коробку и разложить ее на листе бумаги. Нанесите карандашом шаблон, обведя по контору готовую модель. После этого согните лист в нужных гранях и вырежьте его. Далее остается просто склеить модель в той же последовательности, в которой была собрана коробка.
Техника работы со склеиванием модели довольно проста и при наличии практики создаст у ребенка базовое восприятие пространственного мышления. Если модель не получилась с первого раза, проанализируйте ошибку и посмотрите, где неправильно согнута линия или где нужно что-то переделать. Мы уверенны, следующая модель обязательно получиться.
Несколько базовых шаблонов позволит вам быстро и без лишних заморочек создать множество интересных подделок на тему объемного прямоугольника, а главное, позволит занять детей интересным и познавательным делом! Особенно хорошо идея понравиться деткам дошкольного и школьного возраста.
Украсить одежду, декорировать дом или замаскировать дырку на ткани поможет аппликация из ткани своими руками. Техника позволяет быстро, качественно изготовить безделушки, декор хранит свой вид дольше, чем бумажный.

К рукоделию можно привлекать даже детей, умеющих держать ножницы в руках. Предлагается несколько разновидностей, способов создания аппликации из ткани.

Выбор ткани под основу
Основная ткань играет важную роль в выполнении аппликации. Не все подходят для этой цели. Например, не стоит отдавать предпочтение нежному вискозному трикотажу, произойдет его растяжение, потеря формы. С этой задачей замечательно справляется лен с хорошей жесткостью либо рогожка, на ней можно выполнить даже жаккард.

Поэтому стоит останавливать выбор на более жестких тканях, чем сама аппликация. Необязательно у материала должна быть большая толщина и плотность.. Справится даже органза при условии наличия жесткости.

Подходящие материалы для работы
При создании аппликации могут применяться любые ткани и элементы в виде:
- плотной шерсти, твида, полушерстяных. Гладкие аппликации на вещах типа свитеров, жакетов, юбок, жилетов, пальто хорошо получаются из данных материалов.
- мягких трикотажных. Помогут в создании неожиданных драпировок, добавят объема.
- гладких тонких типа хлопка, льна, шелка. Послужат в качестве прекрасных материалов, чтобы сделать акцент цветом или фон для деталей помельче.
- прозрачных типа фатина, органзы, газового шелка, кружева, гипюра для того, чтобы выполнить объемные детали, представленные оборками, воланами, бантами.

Алгоритм при работе с аппликацией
Прежде чем начать заниматься изготовлением поделок в такой технике, следует знать, как сделать аппликацию из ткани, основные действия.

Работа с аппликацией включает следующие этапы:
- Выбор шаблона;
- Определение предпочтительного размера, формы;
- Подбор материалов;
- Выкраивание элементов;
- Подбор фона, если он заранее не выбран;
- Накладывание деталей на фон;
- Фиксация элементов;
- Просушка, если это необходимо.

Соединение элементов: пришить или приклеить?
Соединять аппликацию можно:
- Ручными швами в виде петельного, тамбурного, гладьевых стежков;
- при помощи машинки (выбрать вид строчки (зигзаг), шаг, высоту);
- тканью стигис, имеющую термоклеевой слой. Использование ниток, иголок, клея не является необходимым. Заниматься выполнением аппликации при помощи стигис могут дети;
- приклеивания на пленке. Необходимо запастись пищевой пленкой, двумя кусочками фольги. На доске для глажки собирают многослойный бутерброд из фольги (размер больше мотива, который приклеивается) основы лицом вверх, пищевой пленки (вырезают по контуру мотива, чтобы был запас в 5 см). На минимальной температуре проутюживают, оставляя остывать. Метод идеален для работы с хлопчатобумажными тканями. Готовая вещь может подвергаться ручной стирке, исключая выкручивание.

Советы
Перед началом работы следует правильно подобрать инструменты, материалы. Их качество напрямую влияет на сложность работы, привлекательности изделия. Немаловажным фактором является четкое следование алгоритму действия при работе с аппликацией. Вот некоторые советы для облегчения процесса творения:
- Булавки являются важным инструментом. При помощи них отдельные элементы крепятся к основе. Это позволяет поменять расположение в любой момент, не нанося вреда материалу. Это важно, если мелких элементов много.
- Для пришивания аппликации используют тонкую иголку. Это придает поделке аккуратность, привлекательность.
- Детали изображения лучше фиксировать при помощи хлопчатобумажных ниток.
- Пришивания кусочков около каймы не рекомендуется, это приведет к стягиванию, недостатку места на основе.
- Сложные фигуры типа звезды или других с острым углом требуют предварительной наметки по контуру с окончательным швом.
- Аппликация из ткани невозможна без предварительных эскизов. Шаблоны должны быть в двух вариантах. Можно взять любые картинки, увеличить их на компьютере. Распечатать. Затем перевести на картон, чтобы было удобно обводить на ткани.

Разновидности
Аппликация из ткани представляет:
- Предметную. Аппликация представлена отдельными элементами, собираемыми в одно целое. Может быть в виде листа, ветки, птицы и т.д.
- Сюжетную. Составление данной аппликации происходит таким образом, чтобы было заметно прослеживание совокупности действий, последовательности событий.
- Декоративную. На ткани располагают различные узоры, орнаменты. Таким образов можно декорировать подушки, пледы, покрывала, другие интерьерные предметы.

- Многослойную. Аппликация выполняется из нескольких слоев, накладываемых друг на друга.
- Объемную. Под нее кладется кусочек синтепона или ваты за счет чего аппликация кажется выпуклой. Такая работа требует аккуратной стирки, иначе аппликация потеряет вид.
- Оборотную. Фиксация декоративной заготовки осуществляется с изнанки, а не снаружи.

Мастер- классы
«Крабик»
Потребуются материалы и инструменты в виде:
- любого красного отрезка ткани;
- флизелиновой основы;
- кальки;
- ножниц;
- швейной машинки;
- иголок, ниток;
- эскиза краба;
- одежда для пришивания аппликации.

- Перенос рисунка на бумагу. Если есть отдельные части, то каждая изображается на своем листе. Они не требуют вырезания.
- Под изнанку одежды прикладывают красный отрез. Фиксация деталей при помощи булавок, чтобы было удобно. Верхний завершающий слой – калька с рисунком краба, также зафиксированная.
- Аккуратно прокладывают строчку на машинке по контуру. Окончив работу, кальку убирают. Режущим инструментом удаляют всю лишнюю ткань.
- К полученному изображению добавляют яркие элементы – глаза. К основе прикладывают тканевой кусочек белого цвета, сверху кальку с глазами, фиксируют булавками, сшивают.
- Повторяют предыдущие действия по удалению кальки, срезанию ненужной ткани.
- Остальные элементы добавляются в аппликации по тому же принципу до окончания работы.
- Когда аппликация готова, края прострачивают зигзагом. Можно и воспользоваться специальной краской для батика. Она добавит рельефности, не даст осыпаться.

Мастер- класс по оборотной аппликации
- ткань;
- желаемое изображение;
- инструменты для шитья.

- Подбор изображения для будущей поделки, перенос на отрез противоположного цвета;
- Вырезание полученного шаблона;
- Выворачивание основы на другую сторону, расчерчивание участка для нанесенного рисунка;
- Приметка в данном месте используемой ткани.
- Прошивание кромки изображения с помощью очень маленьких стежков, захватывая основу и лоскут, подлежащий аппликации.
- После смыкания шва удаление булавок, наметочного шва.
- Прорезание контура изображения при помощи хорошего заточенного режущего инструмента.
- Выполнение первого надреза в центре с постепенным расширением.
- Обрезание излишек.

Итак, аппликация из ткани – интересный вид рукоделия, которой поможет в декоре интерьера, одежды. А главное прост в исполнении. Теперь любой лоскуток не останется без внимания.

Все виды параллеле пипедов можно разделить на прямоугольные и наклонные.


Как сделать прямоугольный параллелепипед?
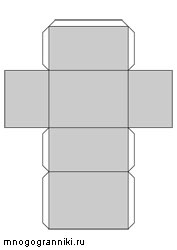

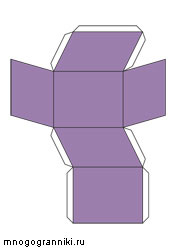
Если вы используете цветной принтер, то предлагаем изготовить параллелепипед, где параллельные грани имеют одинаковые цвета.

по обозначенным линиям.

Приклеив центральный лепесток, получаем:

3. Приклеиваем детали в месте склеивания № 2 и № 3

4. Получаем готовую модель прямоугольного параллелепипеда:
Развертки прямоугольного параллелепипеда







Развертки наклонного параллелепипеда



Сложности запоминания
Бывают случаи, когда слово паралле ле пипед путают со словом параллело грамм .
И, действительно, эти слова созвучны.
Параллело гра́мм — это четырехугольник, у которого противоположные стороны параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб
Параллелограмм - плоская фигура.
Параллеле пипед - объёмное тело, все грани которого - параллелограммы.
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Шутка:
"Иногда, нерадивые ученики пытаются посчитать сколько грамм в параллелограмме и сколько параллельных пипедов в параллелепипеде!"
Популярное
Достаточно часто возникает вопрос о практическом применении бумажных развёрток. Какой смысл в бумажном моделировании?
Изобретение календаря замечательное событие для человечества. То, что год состоит из 12ти месяцев ни для кого не секрет. С тех пор люди самыми различными способами группируют.
Что общего между октаэдром и кубом?
Как вы думаете, что общего у додекаэдра и календаря?
Представьте себе историческое здание, архитектурный ансамбль, который украшают звёздчатые многогранники. И не просто здание, а целый дворец! Возможно ли такое?
В этой статье мы постараемся ответить на вопрос: «Можно ли купить для класса Волшебные грани используя бюджетные средства»?

Что будет, если сложить 6 прямоугольников вместе? Получится прямоугольный параллелепипед, который как ни поверни — одинаково прямоугольный и параллелепипедный. Давайте посмотрим, так ли все просто на самом деле.
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Определение параллелепипеда
Начнем с того, что узнаем, что такое параллелепипед.
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

На рисунке два параллелограмма АВСD и A1B1C1D1. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA1, ВB1, CC1, DD1 параллельны друг другу. Образовавшаяся фигура — параллелепипед.
Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.
Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.
Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.
Параллелепипед — это:
- основание;
- грани;
- ребра;
- диагонали;
- диагонали граней;
- высота.
Свойства параллелепипеда
Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.
Вот 4 свойства параллелепипеда, которые необходимо запомнить:
- Противолежащие грани параллелепипеда равны и параллельны друг другу.
- Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
- Параллелепипед симметричен относительно середины его диагонали.
- Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.
Прямой параллелепипед
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.
Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.
На рисунке: ребро АА1 перпендикулярно основанию ABCD. АА1 перпендикулярна прямым АB и АD, которые лежат в плоскости основания
Свойства прямого параллелепипеда:
- Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
- Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
- Высота прямого параллелепипеда равна длине бокового ребра.
- Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
- Диагонали прямого параллелепипеда точкой пересечения делятся пополам.
На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.
Формулы прямого параллелепипеда:
- Площадь боковой поверхности прямого параллелепипеда
Sб = Ро*h
Ро — периметр основания
h — высота - Площадь полной поверхности прямого параллелепипеда
Sп = Sб+2Sо
Sо — площадь основания - Объем прямого параллелепипеда
V = Sо*h
Прямоугольный параллелепипед
Определение прямоугольного параллелепипеда:
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
На рисунке: основание прямоугольного параллелепипеда ABCD; боковое ребро АА1 перпендикулярно АВСD; угол BAD = 90°
Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.
Свойства прямоугольного параллелепипеда
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.
- Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
- Противолежащие грани параллелепипеда попарно параллельны и равны.
- Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
- Диагонали прямоугольного параллелепипеда равны.
- В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы прямоугольного параллелепипеда:
- Объем прямоугольного параллелепипеда
V = a · b · h
a — длина, b — ширина, h — высота - Площадь боковой поверхности
Sбок = Pосн·c=2(a+b)·c
Pосн — периметр основания, с — боковое ребро - Площадь поверхности
Sп.п = 2(ab+bc+ac)
Диагонали прямоугольного параллелепипеда: теорема
Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.
Если есть теорема, нужно ее доказать. (с) Пифагор
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Доказать теорему.

Доказательство теоремы:
Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.
Все грани прямоугольного параллелепипеда — прямоугольники.
ΔABD: ∠BAD = 90°, по теореме Пифагора
ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора
d² = d₁² + c² = a² + b² + c²
d² = a² + b² + c²
Доказанная теорема — пространственная теорема Пифагора.
Куб: определение, свойства и формулы
Кубом называется прямоугольный параллелепипед, все три измерения которого равны.
Каждая грань куба — это квадрат.

Свойства куба:
- В кубе 6 граней, каждая грань куба — квадрат.
- Противолежащие грани параллельны друг другу.
- Все углы куба, образованные двумя гранями, равны 90°.
- У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
- Диагонали куба равны.
- Диагональ куба в √3 раз больше его ребра.
- Диагональ грани куба в √2 раза больше длины ребра.
Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.
Формулы куба:
- Объем куба через длину ребра a
V = a3 - Площадь поверхности куба
S = 6a2 - Периметр куба
P = 12a
Решение задач
Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a - длина, b - ширина, c - высота. Тогда a = 10, b = 5, c = 8.
Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) - сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) - суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) - сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) - сумма длин всех ребер прямоугольного параллелепипеда.
Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X - сумма длин ребер).
Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Нужно найти длину ребра A1B1.

В фокусе внимания треугольник BDD1.
Угол D = 90°.
По теореме Пифагора:
BD1 2 = DD1 2 + BD 2
BD 2 = BD1 2 – DD1 2
BD 2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD 2 = AD 2 + AB 2
AB 2 = BD 2 - AD 2 = (√17)2 — 4 2 = 1
A1B1 = AB = 1.
Задачка 3. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
AB = 4
AD = 6
AA1= 5
Нужно найти отрезок BD1.

В треугольнике ADB угол A = 90°.
По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD1 угол D = 90°.
BD1 2 = 52 + 25 = 77
BD1 = √77.
Самопроверка
Теперь потренируйтесь самостоятельно — мы верим, что все получится!
Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Вычислите длину ребра AA1.
Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

Если вам сделали сюрприз в подарочной прямоугольной коробке, знайте — это параллелепипед. Кирпич, кстати, тоже яркий пример многогранника с шестью гранями. В этой статье узнаем больше про эту фигуру и дадим примеры разверток для прямоугольного параллелепипеда.
О чем эта статья:
Определение параллелепипеда
Параллелепипед — это многогранник, у которого шесть граней.
У параллелепипеда каждая грань представляют собой параллелограмм, противоположные грани которого равны.

Прямоугольный параллелепипед — это многогранник с шестью гранями, каждая из которых является прямоугольником.
Свойства прямоугольного параллелепипеда
- противоположные грани равны между собой;
- боковые ребра перпендикулярны основаниям, то есть являются высотами.
Диагональ прямоугольного параллелепипеда — это отрезок, который соединяет две противоположные вершины. Все диагонали равны, пересекаются в одной точке и делятся ею пополам.

Схема создания прямоугольного параллелепипеда
Для сборки параллелепипеда нужно распечатать развертку на обычном листе формата А4. Для печати можно использовать белую или цветную бумагу.

Как сделать развертку прямоугольного параллелепипеда:
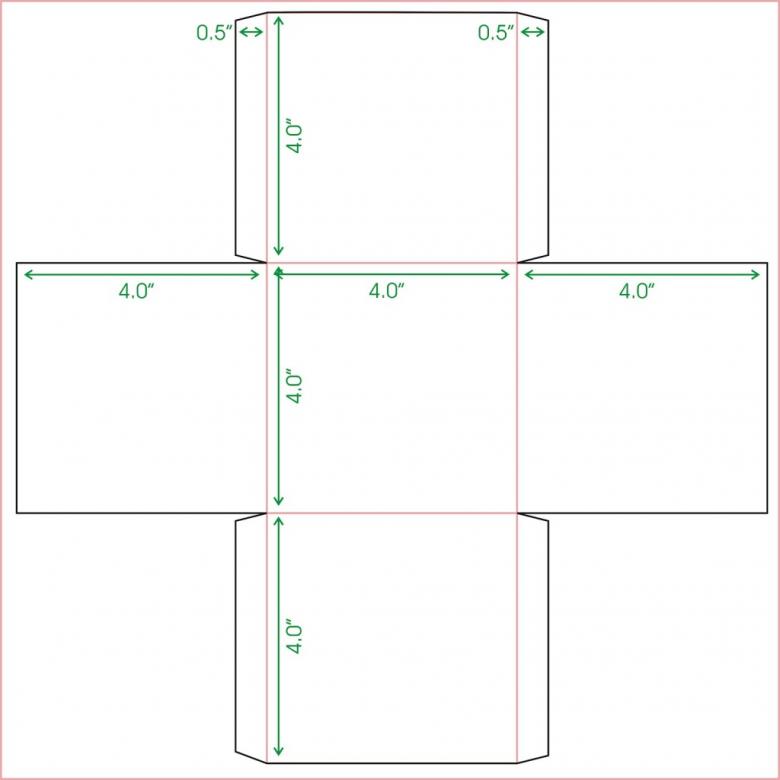
Развертка прямоугольного параллелепипеда с размерами
Геометрические размеры параллелепипеда №1:
- Длина = 120 мм
- Ширина = 90 мм
- Высота = 40 мм
Прямоугольный параллелепипед с такими размерами выглядит так:

Геометрические размеры параллелепипеда №2:
- Длина = 90 мм
- Ширина = 65 мм
- Высота = 50 мм
Прямоугольный параллелепипед с такими размерами выглядит так:

Геометрические размеры параллелепипеда №3:
- Длина = 60 мм
- Ширина = 40 мм
- Высота = 65 мм
Прямоугольный параллелепипед с такими размерами выглядит так:

Так выглядит соотношение размеров параллелепипедов для представленных разверток:

Развертка может пригодиться, если нужно сделать прямоугольный параллелепипед из бумаги или картона на уроке математики в 5 классе. Кроме школьных уроков эти знания пригодятся работникам производств. Например, на заводе по производству упаковки.
Также развертка помогает решать некоторые задачи. Например, находить кратчайшее расстояние между точками на поверхности геометрического тела.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Читайте также:


