Значение целевой функции в задаче о назначениях можно рассчитать с помощью функции ms excel

Обновлено: 08.01.2025

В общем случае задачи формулируются следующим образом:
Имеется N бригад рабочих и M работ, характеризующихся своим временем выполнения. Необходимо распределить работы между бригадами некоторым оптимальным образом.
Кроме того, имеется два варианта задачи:
а) параллельно выполняемые работы;
б) последовательно выполняемые работы.

I. Параллельно выполняемые работы
Параллельность выполнения означает, что работы можно выполнять и одновременно и в любом порядке.
1.1. Примеры
Пример 1.
Имеется N бригад рабочих и M работ, характеризующихся своим временем выполнения. Необходимо распределить работы между бригадами так, чтобы общее время завершения всех работ было минимальным.

Пусть имеется 3 бригады и 9 работ со следующим временем выполнения:

№ работы	Время работы, час
1	40
2	28
3	12
4	26
5	19
6	15
7	12
8	39
9	23

Расставить бригады по работам можно следующим образом:

A	B	C
1	№ работы	Время работы, час	№ бригады
2	1	40	1
3	2	28	1
4	3	12	1
5	4	26	2
6	5	19	2
7	6	15	2
8	7	12	3
9	8	39	3
10	9	23	3
11
12	Бригада 1	80
13	Бригада 2	60
14	Бригада 3	74
15	Макс время	80
16

При этом:
- в ячейке B12 рассчитывается общее время работы первой бригады. Для этого в B12 введена формула:
=СУММЕСЛИ($C$2:$C$10;1;$B$2:$B$10);
- в ячейке B13 рассчитывается общее время работы второй бригады. Для этого в B13 введена формула:
=СУММЕСЛИ($C$2:$C$10;2;$B$2:$B$10);
- в ячейке B14 рассчитывается общее время работы третьей бригады. Для этого в B14 введена формула:
=СУММЕСЛИ($C$2:$C$10;3;$B$2:$B$10);
- в ячейке B15 определяется общее время завершения всех работ. Для этого в B15 введена формула:
=МАКС(B12:B14).

Полученный в B15 результат показывает, что при данной расстановке бригад общее время завершения всех работ составит 80 часов.

Для нахождения более оптимального распределения работ используем средство «Поиск решения».
(вызывается командами:
в Office 2000 Сервис > Поиск решения;
в Office 2007/2010/2013 Данные > Поиск решения)

В окне «Поиск решения» ввести:
- в поле «Установить целевую ячейку» указать B16;
- в поле «Изменяя ячейки» указать C2:C10;
- в окно «Ограничения» с помощью кнопки «Добавить» ввести следующие ограничения:
C2:C10>=1;
C2:C10<=3;
C2:C10=целое
Нажать кнопку «Выполнить».
Система найдет оптимальное решение.

№ работы	Время, час	№ бригады
1	40	3
2	28	3
3	12	2
4	26	2
5	19	1
6	15	1
7	12	2
8	39	1
9	23	2
Бригада 1	73
Бригада 2	73
Бригада 3	68
Макс время	73

Пример 2.
Имеется N бригад рабочих и M работ. Каждая бригада может выполнять любую работу, но с разной производительностью.

Время выполнения, час
Номер работы	Бригада 1	Бригада 2	Бригада 3
1	48	27	1
2	36	1	49
3	37	6	38
4	26	19	45
5	16	30	20
6	2	42	27
7	33	21	26
8	37	2	22
9	28	33	7
10	19	2	42
11	3	3	13
12	49	42	3
13	50	40	36
14	3	41	21

Необходимо распределить работы между бригадами так, чтобы общее время завершения всех работ было минимальным.

Расставить бригады по работам можно так, как указано столбце E.

A	B	C	D	E	F
1	Время выполнения, час
2	Номер работы	Бригада 1	Бригада 2	Бригада 3	Номер бригады	Время выполнения
3	1	48	27	1	1	48
4	2	36	1	49	1	36
5	3	37	6	38	1	37
6	4	26	19	45	1	26
7	5	16	30	20	1	16
8	6	2	42	27	2	42
9	7	33	21	26	2	21
10	8	37	2	22	2	2
11	9	28	33	7	2	33
12	10	19	2	42	2	2
13	11	3	3	13	3	13
14	12	49	42	3	3	3
15	13	50	40	36	3	36
16	14	3	41	21	3	21
17	163
18	100
19	73
20	163

Для определения времени выполнения работы в ячейку F3 введена формула:
=ЕСЛИ(E3=1;B3;ЕСЛИ(E3=2;C3; D3)),
которая скопирована до ячейки F16.
Кроме того:
- в ячейке F17 рассчитывается общее время работы первой бригады. Для этого в F17 введена формула:
=СУММЕСЛИ(E3:E16;1;F3:F16);
- в ячейке F18 рассчитывается общее время работы второй бригады. Для этого в F18 введена формула:
=СУММЕСЛИ(E3:E16;2;F3:F16);
- в ячейке F19 рассчитывается общее время работы третьей бригады. Для этого в F19 введена формула:
=СУММЕСЛИ(E3:E16;3;F3:F16);
- в ячейке F20 определяется общее время завершения всех работ. Для этого в F20 введена формула:
=МАКС(F17:F19).
Полученный в F20 результат показывает, что при данной расстановке бригад общее время завершения всех работ составит 163 часа.

Для нахождения более оптимального распределения работ используем средство «Поиск решения».
В окне «Поиск решения» ввести:
- в поле «Установить целевую ячейку» указать F20;
- в поле «Изменяя ячейки» указать E3:E16;
- в окно «Ограничения» с помощью кнопки «Добавить» ввести следующие ограничения:
E3:E16>=1;
E3:E16<=3;
E3:E16=целое
Нажать кнопку «Выполнить».
Система найдет оптимальное решение.

Задача о наилучшем распределении некоторого числа работ между таким же числом исполнителей. При ее решении ищут оптимальное назначение из условия максимума общей производительности, которая равна сумме производительности исполнителей. Наиболее эффективным методом ее решения является венгерский метод. Задача о назначениях имеет много интерпретаций: распределение работ между механизмами, распределение целей между огневыми средствами для максимизации математического ожидания числа пораженных целей или среднего ущерба и т.д.

1. Задача (формулировка).

Мы будем проще (в терминах). =)

Представим себе задачу: нужно эффективным образом реализовать некоторый относительно большой проект. Для проекта была отобрана команда первоклассных разработчиков, разбирающихся в различных областях. И так уж посчастливилось, что есть сведения (накопленная статистика) о степени (эффективности) владения технологиями для каждого. Но, к сожалению, разработчиков в команде не так уж и много, а точнее – столько же, сколько и технологий будет использовано в проекте.

Необходимо: самым эффективным способом задействовать наибольшее количество технологий, назначив каждому разработчику свою задачу. т.е. оптимально распределить между ними области ответственности за технологии, принимая во внимание их личные способности.

2. Подход к решению

In the end, all business operations can be reduced to three words: people, product, and profits ©. Если мы попробуем изобразить поставленную перед нам и задачу на листе бумаги, то наверняка получим подобную иллюстрацию, как на рисунке (с такими картинками).

Получился — граф. Вершины слева – разработчики, вершины справа – технологии (задачи). Ребра, которые их соединяют – означают то, насколько разработчик в ней разбирается. Эти цифры, т.е. степень владения разработчиком данной технологией, очень важны, но к ним обратимся чуть позже. А пока мы уже верно наметили направление, в котором эффективно решается данная задача:

3. Графы

Самые основы графов были изложены в статье (max cost), поэтому сразу перейду к терминологии, касающейся данной задачи:

Двудольный граф – граф, у которого существует такое разбиение множества вершин на две части (доли), что концы каждого ребра принадлежат разным долям. В нашей задаче тоже есть четкое разделение: одни вершины – это разработчики, другие – задачи, и связи (эффективность владения) есть только между разработчиками и задачами.
Паросочетанием неориентированного графа G называется подмножество M его ребер E, выбранное так, что никакие два ребра из M не являются смежными, т.е. не имеют общей вершины. В терминах нашей задачи синонимом этому будет «назначение», чтобы каждый задействованный разработчик взял на себя отдельную задачу. И не получилось такого, что два разработчика прорабатывают одну проблему, или один «бедняга» отвечал за две задачи.

В теории графов наша проблема, как это ни странно, называется Задачей о Назначениях (ЗН). =) Она является частным случаем задачи нахождения максимального паросочетания. В самом деле, мы ведь стремимся максимально задействовать ресурсы, чтобы одновременно прорабатывалось максимальное число технологий, поэтому в терминах графов — пытаемся найти «максимальное паросочетание», составить максимальное количество пар разработчик-задача.

4. Максимальное паросочетание

Чтобы упростить себе жизнь, мы пока не обращаем внимания на способности людей. Просто хотим каждому подыскать работу. Нескольким первым попавшимся под руку разработчикам предложить работать со знакомой им технологией не составит проблем. Продолжая в том же духе, мы распределим еще несколько задач, но построенное таким образом паросочетание вряд ли будет максимальным. Возможна ситуация как та, что изображена на рисунке:

Как же увеличить паросочетания (назначения)?

если нашли свободную – поиск завершен
если задача уже кому-то назначена, то пройдя по этому ребру паросочетания, попытаемся «переназначить» технологию разработчику, участвующему в данном назначении

Добавим еще немного терминологии из теории графов, простыми словами:

Экспонированная вершина – это вершина, которая не участвует в текущем паросочетании. Т.е. либо «незадействованный разработчик», либо «свободная задача».
Альтернирующая цепь – это цепь, ребра которой попеременно лежат или не лежат в паросочетании. (…- владение технологией – назначенная задача – владение технологией – назначенная задача — …)
Альтернирующее дерево – дерево, состоящее из альтернирующих цепей
Аугментальная цепь – это такая альтернирующая цепь, начальная и конечная вершины которой экспонированы. Вот как называется то, что мы и ищем! =)
Аугментальное дерево – соответственно дерево, в котором хотя бы одна из веток – это аугментальная цепь.

Вот и нашли способ наращивать паросочетание, стремясь получить максимальное. Нужно строить альтенирующее дерево. Когда оно станет аугментальным, искать аугментальные цепи из «незадействованного разработчика» в «свободную задачу» и потом «переназначать» задачи вдоль них. Это выгодно, т.к. увеличивает количество «задач в обработке» на 1:

Теперь мы уже сможем задействовать наибольшее количество технологий в проекте. Самое время принять во внимание еще одно важное условие поставленной перед нами проблемы: эффективность владения технологиями. Мы ведь хотим оптимально назначить всем задачи.

5. Венгерский метод.

Найти решение с максимальной суммарной эффективностью (стоимостью). Звучит, в некотором смысле, похоже на задачу об оптимальной упаковке рюкзака. Наводит на мысль. Вот если бы нам представилась возможность действовать по принципу «жадных алгоритмов».

Мы бы для начала всем разработчикам до упора назначили задачи в соответствии с их максимальными способностями. Если всем разработчикам удалось сразу же распределить задачи — отлично. Но такое происходит не часто. Вдруг два человека, оптимально владеют одной и той же технологией, кому она достанется и что делать в этой ситуации? Одному из разработчиков нужно будет подыскать иную свободную задачу, так же наиболее соответствующую его способностям. Если при текущих (максимальных требованиях) условиях не найдется свободной задачи, то нужно будет попробовать подыскать среди задач, предварительно немного занизив наши требования. Как бы искусственно занизить способности разработчиков в графе. Если в таких условиях обнаружим свободную задачу – получим аугментальное дерево. «Поменяем» по цепочке паросочетания, после чего будет +1. И продолжим назначать таким вот оптимальным образом, пока всем не подыщем работу.

Стратегия ясна.

Мы почти разгадали принцип Венгерского алгоритма. Но как все же построить решение по принципу «жадных алгоритмов»: до упора назначить по max способностям, потом чуть занизить способности и добавив к рассмотрению новые задач, до упора назначить их, занизить… и.т.д.? Как оценить способности и оптимальность текущего назначения?

Вся «фишка» этого алгоритма заключается в следующем. Нам дан всего один параметр в графе – эффективность решения определенной задачи разработчиком, что указано на ребрах. Эта величина присвоена парам разработчик-задача. Мы же «разделим» (отделим от пар) эти величины на две. Искусственно добавим два дополнительных параметра. Одни величины будут приписаны вершинам задач, другие — вершинам разработчиков.

у разработчиков мы укажем их «способности», допустим в единицах «сил», просто указывающие на то, насколько эффективно мы можем их задействовать или задействовали.
у задач мы укажем их «изученность», или, если можно так выразиться, «переизбыток внимания». Этот параметр будем так же измерять в «силе». Переизбыток внимания к задаче возникает в следующей ситуации. Если мы какого-то разработчика «недогрузили», т.е. он способен решать задачу на 5, а ему досталась всего на 3. То у него остается еще 2 «силы» которые он, в принципе, может уделить какой-то из знакомых ему задач. Бегать между кабинетов, консультировать по телефону, давать советы тем, кто занимается любимой ему технологией.

Таким образом, величины указанные на ребрах мы «разделим» на 2 значения, приписанных уже вершинам: эффективность решения задачи = способность разработчика + изученность задачи. В принципе, логично. Чем способней разработчик или чем более известна технология, тем лучше будет реализована эта часть в проекте. Эффективней.

В конце, после того как мы найдем решение, мы конечно будем учитывать только величины на ребрах, но сейчас эта «фишка» поможет нам найти решение. =)

6. Описание алгоритма

Инициализируем граф. Будучи «упертыми оптимистами», мы для каждого разработчика рассчитаем его максимальную «способность» по знакомым ему технологиям, и присвоим ему это число. Everyone enjoys doing the kind of work for which he is best suited ©. О задачах пока ничего неизвестно, поэтому их «изученность» инициализируем нулями.

При поиске «свободной задачи» для «незадействованного разработчика» мы ограничимся теперь только (назовем их) оптимальными ребрами графа, т.е. теми, для которых выполняется равенство: эффективность решения задачи (ребро) = способность разработчика (вершина) + изученность задачи (вершина) .

Удалось обнаружить свободную задачу. Дерево стало аугментальным. «Переназначаем» задачи, наращиваем паросочетание. Начинаем строить альтернирующее дерево заново, т.к. мало ли как там граф изменился
Мы не нашли (не достигли) свободную задачу по оптимальным ребрам. А она есть, т.к. начинали ведь мы со свободного разработчика, а в графе у нас одинаковое количество задач и разработчиков. Полученное альтернирующее дерево становится, так называемым, Венгерским (весь метод так же называется). В данном случае нам нужно будет немного понизить наши требования к разработчикам и начать поиски заново. Failure is simply the opportunity to begin again, this time more intelligently (с).

Незадействованные разработчики, т.к. именно с них мы начинаем стоить дерево
Разработчики и задачи, до которых можно дотянуться по оптимальным ребрам из незадействованных разработчиков. Т.к. именно через их «переназначение» мы пытаемся трудоустроить последних.

Разработчики и задачи, находящиеся в паросочетании, но недоступные из свободных вершин (разработчиков). Нашли им работу – нечего их пока трогать.
Задачи, недостижимые по оптимальным ребрам – до них нам и нужно будет добраться. Поэтому при построении дерева мы будем отмечать вершины, в которые удалось попасть. А эти задачи, соответственно, останутся неотмеченными.

Понизим способности разработчиков на delta, чтобы «присоединить» наименее безболезненным способом, по крайней мере, одно ребро к альтернирующему дереву, по которому в следующий раз будем продолжать поиски свободной задачи
Повысим «изученность» задач на delta, чтобы внутри уже сейчас построенного аугментального графа ребра — остались оптимальными. Т.е. чтобы сохранилось равенство: эффективность решения задачи (ребро) = способность разработчика (вершина) + изученность задачи (вершина)

Все. Все шаги данного метода рассмотрены. Продолжаем в том же духе… Success is not final, failure is not fatal: it is the courage to continue that counts.

7. Алгоритм словами, очень кратко

Инициализация. Разработчикам – max способности. Задачи – не изучены.
Пока не всем разработчикам нашли задачи.
- Пока удается построить аугментальное дерево (находить свободные задачи) по оптимальным ребрам
  - «Переназначаем» задачи, увеличивая паросочетания
  - Понижаем способности разработчиков на min величину
  8. Листинг
  
  Код, конечно, будет покороче, чем все мое описание. =)
  
  Я взял его здесь. На мой взгляд, очень хорошая реализация. Единственное отличие, у автора приведен код метода минимизации назначений (если, допустим, на ребрах – зарплата), а в статье мы распределяли задачи с целью получения максимальной эффективности. Поэтому, слегка модифицировав код, приведу ниже реализацию максимального метода:
  
  int n;
  vector < vector< int > > a; // Матрица эффективности a[разраб][задача]
  vector< int > xy, yx; // Паросочетания: xy[разраб], yx[задача]
  vector< char > vx, vy; // Альтернирующее дерево vx[разраб], vy[задача]
  vector< int > maxrow, mincol; // Способности, изученность
  
  bool dotry ( int i) if (vx[i]) return false ;
  vx[i] = true ;
  for ( int j=0; j<n; ++j)
  if (a[i][j]-maxrow[i]-mincol[j] == 0)
  vy[j] = true ;
  for ( int j=0; j<n; ++j)
  if (a[i][j]-maxrow[i]-mincol[j] == 0 && yx[j] == -1) xy[i] = j;
  yx[j] = i;
  return true ;
  >
  for ( int j=0; j<n; ++j)
  if (a[i][j]-maxrow[i]-mincol[j] == 0 && dotry (yx[j])) xy[i] = j;
  yx[j] = i;
  return true ;
  >
  return false ;
  >
  
  mincol.assign (n, 0);
  minrow.assign (n, 0);
  for ( int i=0; i<n; ++i)
  for ( int j=0; j<n; ++j)
  maxrow[i] = max (maxrow[i], a[i][j]);
  
  xy.assign (n, -1);
  yx.assign (n, -1);
  for ( int c=0; c<n; ) vx.assign (n, 0);
  vy.assign (n, 0);
  int k = 0;
  for ( int i=0; i<n; ++i)
  if (xy[i] == -1 && dotry (i))
  ++k;
  c += k;
  if (k == 0) int z = INF;
  for ( int i=0; i<n; ++i)
  if (vx[i])
  for ( int j=0; j<n; ++j)
  if (!vy[j])
  z = min (z, maxrow[i]+mincol[j]-a[i][j]);
  for ( int i=0; i<n; ++i) if (vx[i]) maxrow[i] -= z;
  if (vy[i]) mincol[i] += z;
  >
  >
  >
  
  int ans = 0;
  for ( int i=0; i<n; ++i)
  ans += a[i][xy[i]];
  printf ( "%d\n" , ans);
  for ( int i=0; i<n; ++i)
  printf ( "%d " , xy[i]+1);
  >
  
  * This source code was highlighted with Source Code Highlighter .
  
  9. Итого
  
  Если кто-то видит Венгерку впервые. И после прочтения описания, а за ним листинга – возникнет уверенное впечатление «да тут по листингу и без этих описаний все понятно, что было распинаться». Буду все же надеяться, что хоть отчасти описание добавило понимания в работу алгоритма. Буду искренне рад за Вас! а мне, в свою очередь, это немного даст почувствовать, что писал, наверное, не зря. =)
  
  ЗАДАЧА О НАЗНАЧЕНИЯХ И НЕКОТОРЫЕ СПОСОБЫ ЕЕ РЕШЕНИЯ
  1 Филиал Южного федерального университета в г.Новошахтинске Текст работы размещён без изображений и формул.
  Полная версия работы доступна во вкладке "Файлы работы" в формате PDF
  При решении некоторых задач менеджмента приходится назначать исполнителей (людей, механизмы и т.п.) для выполнения некоторых однотипных работ. При этом дополнительно известны значения с_ij - эффективность (неэффективность) выполнения i-м исполнителем j-ой работы. Требуется распределить исполнителей по работам таким образом, чтобы максимизировать (минимизировать) суммарный критерий эффективности (неэффективности) выполнения всех работ.
  
  Данная задача носит название «задача о назначениях» и является частным случаем более общей транспортной задачи. Если число исполнителей равно числу выполняемых работ, то такая задача является сбалансированной, в противном случае - не сбалансированной. В случае сбалансированной задачи о назначениях выполняются два условия: каждый исполнитель выполняет только одну работу и каждая работа выполняется только одним исполнителем.
  
  Для решения сбалансированной задачи о назначениях можно предложить следующий простой алгоритм: на каждом шаге назначений, начиная с первого исполнителя, выбирать самого эффективного (неэффективного). Однако такой способ решения, при всей кажущейся очевидности, не приводит, как правило, к получению оптимального решения: выбор на первых шагах самых эффективных (неэффективных) исполнителей заставляет нас на последних шагах алгоритма выполнять назначения, которые вносят негативный вклад в суммарный критерий.
  
  Рассмотрим следующий пример: имеется четыре исполнителя (И), которых необходимо распределить для выполнения четырех работ (Р) таким образом, что бы минимизировать суммарную себестоимость выполнения всех работ. Матрица себестоимостей С_4х4 имеет вид:
  
  Суммарная себестоимость выполнения всех работ, найденная по предложенному алгоритму, составила 10+20+55+100=185 условных единиц.
  
  10
  
  20
  
  55
  
  100
  
  При этом видно, что назначение на первых шагах исполнителя И₁ на работу Р₃, а исполнителя И₂ на работу Р₁ и т. д. привело к тому, что на последнем шаге нам "пришлось" назначить исполнителя И₄ на работу Р₄ с максимальным значением себестоимости с_ij.
  
  Получаемое значение суммарной себестоимости зависит при этом от порядка, в котором мы выполняем наши назначения. Если, при той же матрице себестоимости, мы будем выполнять последовательные назначения начиная с исполнителя И₄, то суммарная себестоимость составит уже 20+15+35+25=95 условных единиц, что демонстрирует следующая матрица
  
  25
  
  35
  
  15
  
  20
  
  Таким образом, алгоритм «выбирай на каждом шаге самого эффективного (неэффективного)» не может использоваться при принятии управленческих решений.
  
  Решим задачу о назначениях с помощью электронных таблиц MS Excel, используя надстройку «Поиск решения», сформулировав ее как задачу линейного программирования.
  
  Выполним математическую постановку сбалансированной задачи о назначениях, для чего:
  
  1. Определим неизвестные и их количество.
  
  Рассмотрим переменные x_ij, которые равны 1, если i-й исполнитель назначен на выполнение j-ой работы и 0, если он не назначен i=1,2. n j=1,2. n. Таким образом, значения x_ij образуют матрицу назначений X_nxn, состоящую из нулей и единиц.
  
  2. Запишем критерий оптимизации (целевую функцию) - суммарную эффективность (неэффективность) выполнения всех работ.
  
  Целевая функция задачи о назначениях зависит от неизвестных пока переменных x_ij и известны значений с_ij - эффективности (неэффективности) выполнения i-м исполнителем j-ой работы и запишется в следующем виде
  
  3. Сформулируем ограничения рассматриваемой задачи.
  
  а) каждый исполнитель выполняет только одну работу. Выполнение данного условия означает, что каждая строка матрицы назначений Х содержит только одно значение равное единицы, а все остальные равны нулю. Т.е. сумма элементов каждой строки матрицы назначений Х равна 1, и это ограничение можно записать в виде системы n уравнений
  
  или в общем виде
  
  б) каждая работа выполняется только одним исполнителем. Выполнение данного условия означает, что каждый столбец матрицы назначений Х содержит только одно значение равное единицы, а все остальные равны нулю. Т.е. сумма элементов каждого столбца матрицы Х равна 1, и это ограничение можно записать в виде системы n уравнений
  
  или в общем виде
  
  в) двоичность (бинарность) переменных x_ij. Так как областью допустимых изменений каждой переменной является не множество целых неотрицательных чисел, а конечное множество (0,1)
  
  то мы получаем дискретную задачу оптимизации.
  
  Таким образом, целевая функция (1) и ограничения (2-4) составляют математическую модель сбалансированной задачи о назначениях.
  
  Решим пример, приведенный выше, с помощью ЭТ MS Excel, для чего:
  
  1. Запишем матрицу себестоимостей С_4х4.
  
  2. Сформируем матрицу назначений Х_4х4 с пока нулевыми значениями переменных x_ij.
  
  3. Дополним матрицу назначений Х4х4 столбцом справа и строкой снизу, в ячейки которых запишем формулу суммировании элементов строк и столбцов матрицы Х. Это понадобится нам при учете ограничений (2) и (3) задачи. При этом возможно использование кнопки «Сумма»
  
  4. Используя формулу (1), запишем целевую функцию - суммарную себестоимость выполнения всех работ. При этом возможно использование встроенной функции MS Excel «СУММПРОИЗВ».
  
  Т.к. все переменных x_ij пока равны нулю, то и вычисленное значение целевой функции - ноль.
  
  Лист MS Excel с исходными данными для решения представлен ниже.
  
  5. С помощью команды Главного меню «Данные» вызвать диалоговое окно надстройки «Поиск решения» и выполнить необходимые установки.
  
  6. Щелчком по кнопке «Выполнить» запустить надстройку и сохранить полученное решение.
  
  Анализ полученного решения показывает, что оно в точности совпадает с решением, полученным по алгоритму «выбирай на каждом шаге самого эффективного (неэффективного)», когда мы начали назначения с исполнителя И₄. Это говорит о том, что возможно интуитивное принятие оптимального решения, однако при увеличении размерности задачи и возрастании цены ошибки целесообразно применение математических методов и ЭВМ для принятия управленческих решений.
  
  Рассмотрим теперь решение не сбалансированной задачи о назначениях, когда число исполнителей n не равно числу выполняемых работ m. При этом возможны два случая:
  
  1) число исполнителей n больше числа выполняемых работ m (n > m),
  
  2) число исполнителей n меньше числа выполняемых работ m (n < m).
  
  В обоих случаях для решения не сбалансированной задачи ее сводят к сбалансированной, путем введения фиктивных работ или фиктивных исполнителей с нулевыми значениями с_ij - эффективности (неэффективности) выполнения i-м исполнителем j-ой работы. В первом случае, когда n > m, вводится k = n - m фиктивных работ P_m₊₁, P_m₊₂, . P_m₊_k. Во втором случае (n < m) - рассматриваются k = m - n фиктивных исполнителя И_n₊₁,И_n₊₂, . И_n₊_k.
  
  Решим задачу о назначениях, когда шесть исполнителей претендуют на выполнение четырех работ. Листы MS Excel с исходными данными и полученным решением представлены ниже.
  
  Анализ полученного решения показывает, что исполнители И₂ и И₅ к работам не допущены (назначены на выполнение фиктивных работ Р₅ и Р₆ соответственно). Оставшиеся исполнители обеспечили выполнение четырех работ с минимально возможной суммарной себестоимостью 10+15+30+30=85 условных единиц.
  
  Рассмотрим последнюю задачу о назначениях, когда четыре исполнителя претендуют на выполнение шести работ (n < m). Лист MS Excel с исходными данными и диалоговым окном надстройки «Поиск решения» представлены ниже.
  
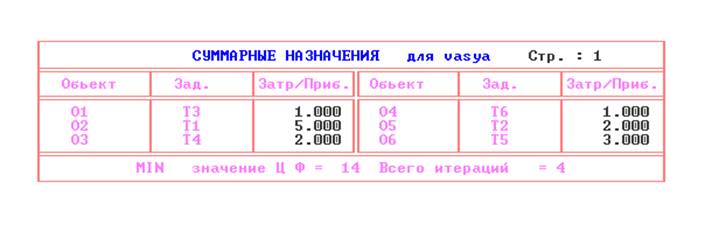
  Анализ представленного ниже решения показывает, что работы Р₄ и Р₆ не выполняются, а четыре исполнителя распределены по оставшимся четырем работам таким образом, что минимальная суммарная себестоимость составила 10+20+10+30=70 условных единиц.
  
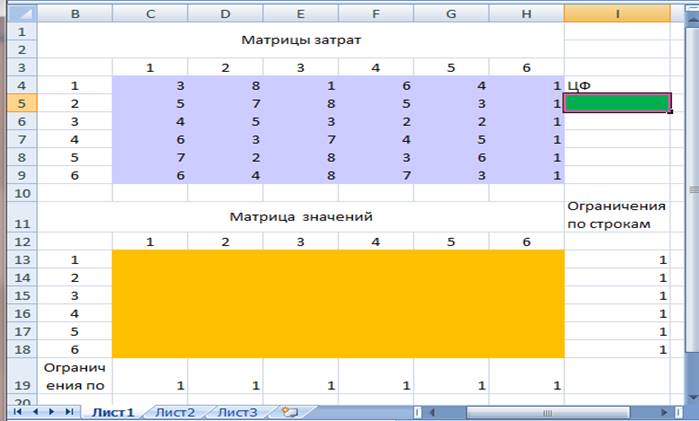
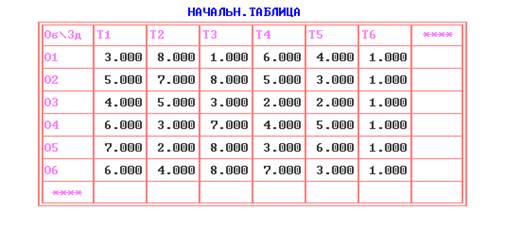
  Имеется 6 исполнителей, которые могут выполнять 6 различных работ.
  
  Известны затраты, связанные с назначением i - го исполнителя на j – ю работу, задаваемые матрицей (c i j ) размерностью 66 ( i, j 16 ).
  
  Необходимо произвести назначение исполнителей на работы таким образом, чтобы общие затраты всех назначений были бы минимальными, при условии, что каждый исполнитель может быть назначен только на одну работу и за каждой работой может быть закреплен только один исполнитель.
  
  Автоматизация решения задачи о назначениях в MS Excel
  
  Данная задачa, которая является совершенно полной и может быть решена с использованием модуля «Поиск решения» электронных таблиц MS Excel. Для этого расположим данные на листе Excel как показано на рис.1.
  
  рис.1
  
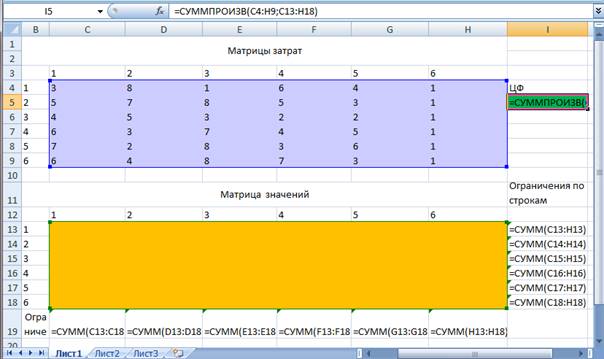
  Матрица затрат задана массивом чисел C4:H9, матрица назначений (переменных) – массивом C13:H18, формулы для целевой функции и основных ограничений – по строкам и столбцам матрицы переменных – указаны в соответствующих ячейках на рис.2.
  
  рис.2
  
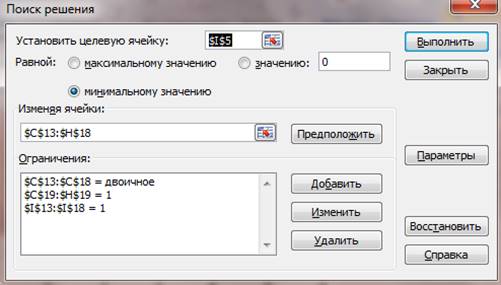
  В результате, после ввода всех формул, массивов и ограничений окно модуля «Поиск решения» выглядит так, как показано на рис. 3
  
  рис.3
  
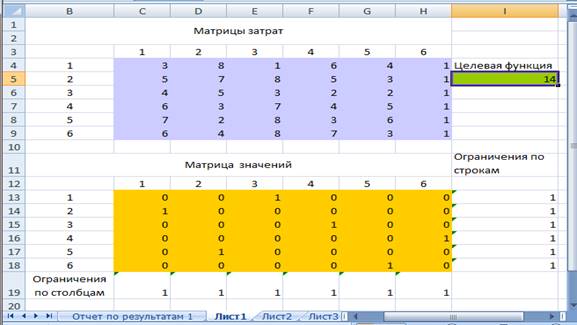
  После ввода необходимых параметров «Линейная модель» модуль «Поиск решения» запускается на решение задачи, а его результат представлен на рис.4.
  
  рис.4
  
  Автоматизация решения задачи о назначениях в ПЭР
  
  Для решения этой задачи в среде ПЭР необходимо в главном меню программы выбрать пункт «Задача о назначениях».
  
  Далее в режиме ввода новой задачи ввести в ПЭР все необходимые параметры задачи.
  
  После чего ввести числовые данные задачи.
  
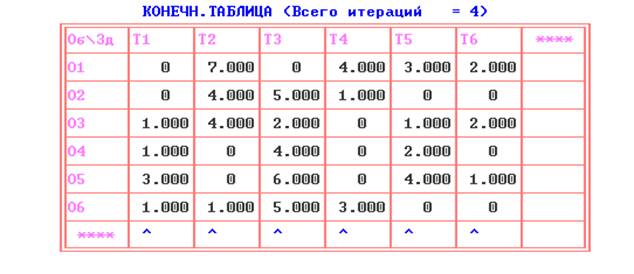
  После того, как данные задачи будут сформированы необходимо войти в режим решения задачи о назначениях функционального меню ПЭР и вывести таблицы всех итераций решения данной задачи. Начальная таблица приведена на рис.4
  
  рис.4
  
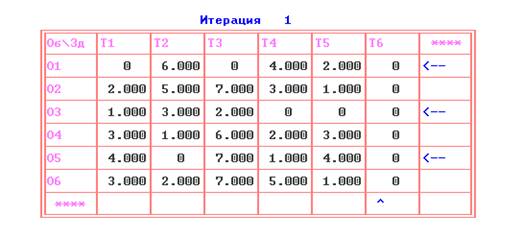
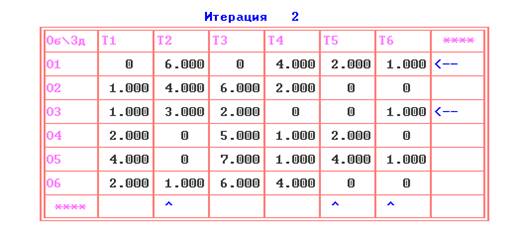
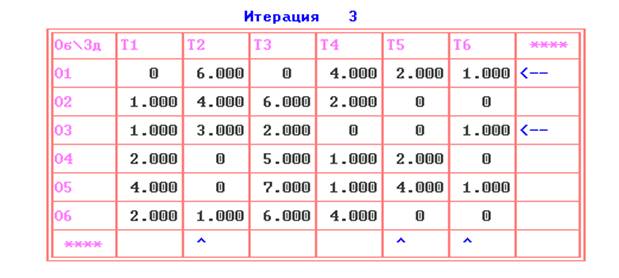
  На первой итерации ПЭР «получает» приведенную матрицу.
  
  Специальными стрелками в последних строке и столбце таблицы первой итерации обозначены вертикальные и горизонтальные лини зачеркивания.
  
  рис.5
  
  рис.6
  
  рис.7
  
  На первой итерации ПЭР «получает» приведенную матрицу.
  
  Специальными стрелками в последних строке и столбце таблицы первой итерации обозначены вертикальные и горизонтальные лини зачеркивания.
  
  рис.8
  
  Однако, сам план назначений в табличной форме выводится отдельно как показано на рис.9
  
  рис.9
  
  Автоматизация решения задачи о назначениях в программе Venger
  
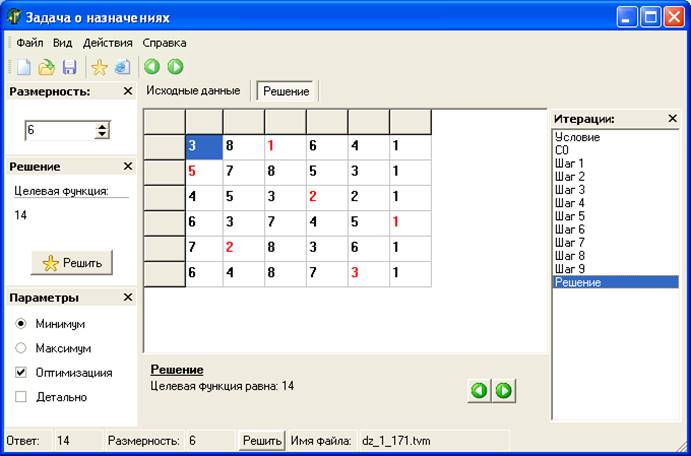
  Программа Venger разработана специально для автоматизации процесса решения задачи о назначениях по алгоритму венгерского метода и предназначена для использования в среде ОС Windows.
  
  На итерации «Решение» отображается исходная матрица эффективностей назначений, в которой красным цветом выделены элементы, соответствующие единичным элементам матрицы назначений.
  
  Выделенные элементы являются слагаемыми оптимального значения целевой функции данной задачи.
  
  рис.10
  
  v Приобретение навыков построения математической модели задачи о назначениях.
  
  v Приобретение навыков автоматизированного решения задачи о назначениях в среде программ Microsoft Excel и ПЭР.
  
  v Приобретение навыков автоматизированного решения задачи о назначениях по алгоритму венгерского метода в среде программы Venger.
  
  Читайте также:

8. Листинг

9. Итого

ЗАДАЧА О НАЗНАЧЕНИЯХ И НЕКОТОРЫЕ СПОСОБЫ ЕЕ РЕШЕНИЯ