Жадный алгоритм в эксель
Это частный случай "задачи о рюкзаке", т.к. необходимо найти не оптимальный перечень слагаемых, а любую возможную комбинацию, удовлетворяющую заданным условиям. Думаю, что задача может иметь практическое применение.
У меня были некоторые наработки на эту тему, решил их доработать и опубликовать, а также хочется получить дополнительные материалы по эффективным алгоритмам.
Считаю, что данную задачу нужно решать с помошью макросов (все решения через поиск решения или формульные варианты не рассматриваю).
На текущий момент, самый быстрый способ решения, который мне попадался - это "макрос Слэна", но у него есть недостаток, решение не всегда может быть найдено. Как именно работает макрос я не разобрался, но думаю, что в основе лежит "жадный алгоритм" с перебором.
Если есть ссылки на хорошие алгоритмы или реализации, прошу поделиться
Прилагаю файл с разными решениями:
1. Случайная выборка, не самый лучший вариант, но может и он сгодиться
2. С применением динамического программирования. Сумма находится по целочисленным слагаемым, работает относительно быстро и если может быть решение - оно будет найдено. Скорость, а также объем выделяемой памяти сильно зависят от искомой суммы, в макросе введено ограничение - сумма не должна превышать 80 000 000. Подходит для решения дробных сумм, например, рубли с копейками, достаточно все суммы умножить на 100.
3. Преребор (brute force), возможно указать ограничения по количеству слагаемых, а также отсекает неоптимальные ветви решения, что позволило сделать приемлемый по скорости перебор, находит все решения подходящие под условия. Но для большого количества слагаемых метод не применим
4. Макрос Слэна, хороший быстрый алгоритм, но не всегда находит решение.
Реализация не окончательная, поэтому в готовые решеня не размещаю.
Хочется найти еще эффективные и быстрые варианты решения. Например, можно совместить частичный перебор с динамикой
UPD 27.02.2014: Обновлен алгоритм с перебором, стал существенно быстрее работать
Это частный случай "задачи о рюкзаке", т.к. необходимо найти не оптимальный перечень слагаемых, а любую возможную комбинацию, удовлетворяющую заданным условиям. Думаю, что задача может иметь практическое применение.
У меня были некоторые наработки на эту тему, решил их доработать и опубликовать, а также хочется получить дополнительные материалы по эффективным алгоритмам.
Считаю, что данную задачу нужно решать с помошью макросов (все решения через поиск решения или формульные варианты не рассматриваю).
На текущий момент, самый быстрый способ решения, который мне попадался - это "макрос Слэна", но у него есть недостаток, решение не всегда может быть найдено. Как именно работает макрос я не разобрался, но думаю, что в основе лежит "жадный алгоритм" с перебором.
Если есть ссылки на хорошие алгоритмы или реализации, прошу поделиться
Прилагаю файл с разными решениями:
1. Случайная выборка, не самый лучший вариант, но может и он сгодиться
2. С применением динамического программирования. Сумма находится по целочисленным слагаемым, работает относительно быстро и если может быть решение - оно будет найдено. Скорость, а также объем выделяемой памяти сильно зависят от искомой суммы, в макросе введено ограничение - сумма не должна превышать 80 000 000. Подходит для решения дробных сумм, например, рубли с копейками, достаточно все суммы умножить на 100.
3. Преребор (brute force), возможно указать ограничения по количеству слагаемых, а также отсекает неоптимальные ветви решения, что позволило сделать приемлемый по скорости перебор, находит все решения подходящие под условия. Но для большого количества слагаемых метод не применим
4. Макрос Слэна, хороший быстрый алгоритм, но не всегда находит решение.
Реализация не окончательная, поэтому в готовые решеня не размещаю.
Хочется найти еще эффективные и быстрые варианты решения. Например, можно совместить частичный перебор с динамикой
UPD 27.02.2014: Обновлен алгоритм с перебором, стал существенно быстрее работать MCH
Это частный случай "задачи о рюкзаке", т.к. необходимо найти не оптимальный перечень слагаемых, а любую возможную комбинацию, удовлетворяющую заданным условиям. Думаю, что задача может иметь практическое применение.
У меня были некоторые наработки на эту тему, решил их доработать и опубликовать, а также хочется получить дополнительные материалы по эффективным алгоритмам.
Считаю, что данную задачу нужно решать с помошью макросов (все решения через поиск решения или формульные варианты не рассматриваю).
На текущий момент, самый быстрый способ решения, который мне попадался - это "макрос Слэна", но у него есть недостаток, решение не всегда может быть найдено. Как именно работает макрос я не разобрался, но думаю, что в основе лежит "жадный алгоритм" с перебором.
Если есть ссылки на хорошие алгоритмы или реализации, прошу поделиться
Прилагаю файл с разными решениями:
1. Случайная выборка, не самый лучший вариант, но может и он сгодиться
2. С применением динамического программирования. Сумма находится по целочисленным слагаемым, работает относительно быстро и если может быть решение - оно будет найдено. Скорость, а также объем выделяемой памяти сильно зависят от искомой суммы, в макросе введено ограничение - сумма не должна превышать 80 000 000. Подходит для решения дробных сумм, например, рубли с копейками, достаточно все суммы умножить на 100.
3. Преребор (brute force), возможно указать ограничения по количеству слагаемых, а также отсекает неоптимальные ветви решения, что позволило сделать приемлемый по скорости перебор, находит все решения подходящие под условия. Но для большого количества слагаемых метод не применим
4. Макрос Слэна, хороший быстрый алгоритм, но не всегда находит решение.
Реализация не окончательная, поэтому в готовые решеня не размещаю.
Хочется найти еще эффективные и быстрые варианты решения. Например, можно совместить частичный перебор с динамикой
UPD 27.02.2014: Обновлен алгоритм с перебором, стал существенно быстрее работать Автор - MCH
Дата добавления - 25.06.2013 в 01:15
В общем виде задача о рюкзаке формулируется следующим способом: имеется рюкзак определенного объема и неограниченное количество предметов. Для каждого предмета известен его объем (вес) и ценность (стоимость, эффективность). В рюкзак можно положить целое число предметов различного типа. Цель состоит в том, чтобы суммарная ценность всех находящихся в рюкзаке предметов была максимальна, а их объем (вес) не превышал заданной величины. К подобной формулировке может быть сведена задача максимального использования грузоподъемности подвижного состава, грузовместимости судна, автомобиля и т.п. Такая задача часто возникает при выборе оптимального управления в экономико-финансовых областях (например распределение бюджета отдела по проектам).
Решение задачи в классической постановке
Подобные задачи легко решаются с помощью надстройки "Поиск решения". Подготовлены исходные данные (рисунок ниже). Задача состоит в том, чтобы за счет подбора значений ячеек B16:B19 добиться максимального значения целевой функции (значение ячейки D20).
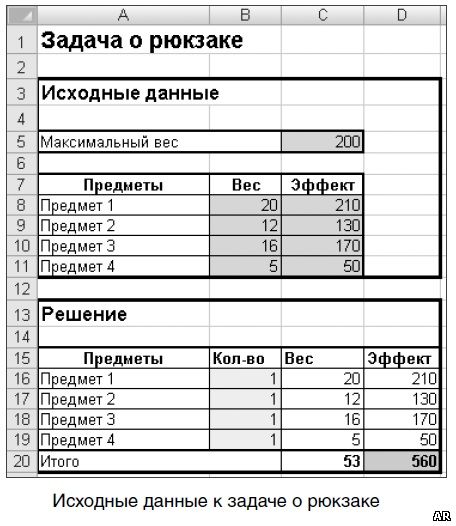
На первом рисунке ниже показаны ограничения на значения изменяемых ячеек. На втором рисунке ниже приводится результат расчета. Во многих практических случаях данная постановка задачи является слишком упрощенной. Далее будут рассмотрены варианты усложнения постановки задачи.
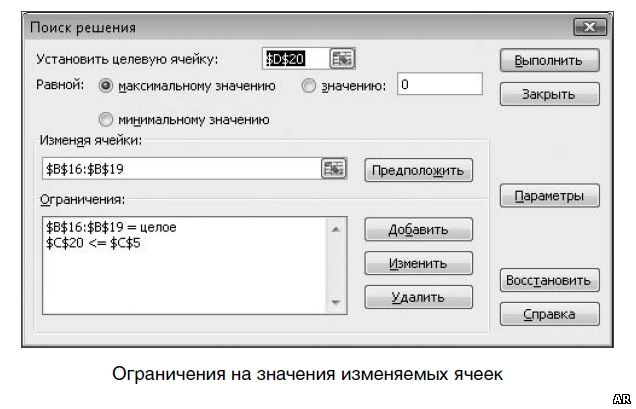

Модифицированная задача
Одним из дополнительных ограничений, возникающих при практическом использовании данной задачи, могут быть ограничения на необходимое количество предметов определенных видов, которые можно положить в рюкзак. При этом могут возникать варианты задачи, когда требуется строго определенное количество предметов или требуется не менее (не более) заданного количества предметов.
На рисунке ниже показаны исходные данные модифицированного варианта задачи. В этом случае предполагается, что в рюкзак может быть положено не менее некоторого количества предметов.
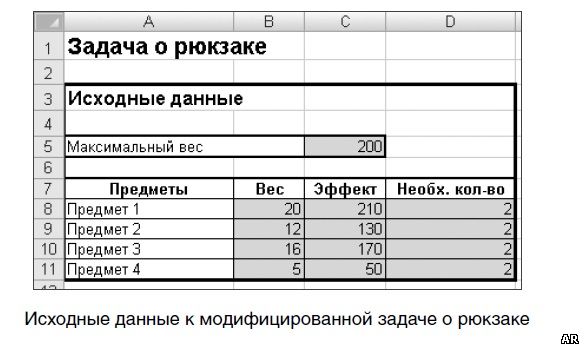
На следующем рисунке показаны ограничения на значения изменяемых ячеек B16:B19. В данном случае к ограничениям добавлено условие 16:19>=8:11, то есть задано минимальное необходимое количество предметов различных видов.

Решение задачи представлено последнем рисунке.

При необходимости дополнительное условие 16:19>=8:11 может быть изменено. Например, можно установить отдельные ограничения для всех предметов, назначив для некоторых из них точное количество предметов, в то время как для других — условие «не менее» или «не более»


= Мир MS Excel/Линейный раскрой - Мир MS Excel
Войти через uID
Войти через uID
Задачу линейного раскроя можно решать разными способами:
1. Полный перебор, как правило, не возможно реализовать в реальных условиях.
2. Самый эффективный способ - целочисленное линейное программирование (метод Гомори, как целочисленный вариант симплекс-метода). В качестве инструмента можно использовать Solver из MS Excel. Но здесь есть ряд ограничений - необходимо найти все варианты сложения исходных деталей, не превышающих размер заготовок (а вариантов может быть несколько тысяч или сотен тысяч). Ограничение Solver'a - 200 изменяемых ячеек.
3. "Жадный" алгоритм. У данного алгоритма есть вариации, основное достоинство - высокая скорость. Применим для быстрой оценки раскроя, либо когда скорость важнее оптимизации.
4. Решать как частный случай задачи о рюкзаке (сумма подмножеств) и выбор наилучшего варианта из имеющихся.
5. Про генетический алгоритм ничего сказать не могу, т.к. не изучал его.
Реализовал собственный алгоритм линейного раскроя в Excel, который основан на решении задачи о рюкзаке (сумма подмножеств) методом целочисленного динамического программирования. Производится генерация различных вариантов раскроя в зависимости от сортировки исходных деталей и заготовок и выбор наилучшего решения.
К достоинству можно отнести - достаточно эффективный результат по сравнению с "жадным" алгоритмом, а также при сравнении с результатом других программ линейного раскроя.
Дополнительно реализовал решение с помощью линейного программирования.
Вначале производится генерация рациональных схем раскроя, затем симплекс-методом находим решение системы, данное решение является оптимальным (использование наименьшего количества заготовок). Далее сводим задачу к максимизации полезного остатка.
Domo -версию программы можно скачать здесь или здесь, она полностью функциональна, доступен расчет с помощью динамического программирования (DP).
Расчет с помощью линейного программирования (LP) отключен.
Также отключена возможность составления и экспорта отчетов.
Можно использовать до 20 различных размеров заготовок и до 90 различных размеров деталей.
Есть возможность задать ширину реза, размер торцевой кромки, размер полезного (делового) остатка, возможность раскраивать в два профиля (если это требуется)
Можно убедиться в эффективности алгоритма раскроя в сравнении с другими программами.
Если будет заинтересованность в алгоритме или потребуется адаптация отчета под ваши требования, то можете обратиться ко мне в личку.
Задачу линейного раскроя можно решать разными способами:
1. Полный перебор, как правило, не возможно реализовать в реальных условиях.
2. Самый эффективный способ - целочисленное линейное программирование (метод Гомори, как целочисленный вариант симплекс-метода). В качестве инструмента можно использовать Solver из MS Excel. Но здесь есть ряд ограничений - необходимо найти все варианты сложения исходных деталей, не превышающих размер заготовок (а вариантов может быть несколько тысяч или сотен тысяч). Ограничение Solver'a - 200 изменяемых ячеек.
3. "Жадный" алгоритм. У данного алгоритма есть вариации, основное достоинство - высокая скорость. Применим для быстрой оценки раскроя, либо когда скорость важнее оптимизации.
4. Решать как частный случай задачи о рюкзаке (сумма подмножеств) и выбор наилучшего варианта из имеющихся.
5. Про генетический алгоритм ничего сказать не могу, т.к. не изучал его.
Реализовал собственный алгоритм линейного раскроя в Excel, который основан на решении задачи о рюкзаке (сумма подмножеств) методом целочисленного динамического программирования. Производится генерация различных вариантов раскроя в зависимости от сортировки исходных деталей и заготовок и выбор наилучшего решения.
К достоинству можно отнести - достаточно эффективный результат по сравнению с "жадным" алгоритмом, а также при сравнении с результатом других программ линейного раскроя.
Дополнительно реализовал решение с помощью линейного программирования.
Вначале производится генерация рациональных схем раскроя, затем симплекс-методом находим решение системы, данное решение является оптимальным (использование наименьшего количества заготовок). Далее сводим задачу к максимизации полезного остатка.
Domo -версию программы можно скачать здесь или здесь, она полностью функциональна, доступен расчет с помощью динамического программирования (DP).
Расчет с помощью линейного программирования (LP) отключен.
Также отключена возможность составления и экспорта отчетов.
Можно использовать до 20 различных размеров заготовок и до 90 различных размеров деталей.
Есть возможность задать ширину реза, размер торцевой кромки, размер полезного (делового) остатка, возможность раскраивать в два профиля (если это требуется)
Можно убедиться в эффективности алгоритма раскроя в сравнении с другими программами.
Если будет заинтересованность в алгоритме или потребуется адаптация отчета под ваши требования, то можете обратиться ко мне в личку. MCH
Реализовал собственный алгоритм линейного раскроя в Excel, который основан на решении задачи о рюкзаке (сумма подмножеств) методом целочисленного динамического программирования. Производится генерация различных вариантов раскроя в зависимости от сортировки исходных деталей и заготовок и выбор наилучшего решения.
К достоинству можно отнести - достаточно эффективный результат по сравнению с "жадным" алгоритмом, а также при сравнении с результатом других программ линейного раскроя.
Дополнительно реализовал решение с помощью линейного программирования.
Вначале производится генерация рациональных схем раскроя, затем симплекс-методом находим решение системы, данное решение является оптимальным (использование наименьшего количества заготовок). Далее сводим задачу к максимизации полезного остатка.
Domo -версию программы можно скачать здесь или здесь, она полностью функциональна, доступен расчет с помощью динамического программирования (DP).
Расчет с помощью линейного программирования (LP) отключен.
Также отключена возможность составления и экспорта отчетов.
Можно использовать до 20 различных размеров заготовок и до 90 различных размеров деталей.
Есть возможность задать ширину реза, размер торцевой кромки, размер полезного (делового) остатка, возможность раскраивать в два профиля (если это требуется)
Можно убедиться в эффективности алгоритма раскроя в сравнении с другими программами.
Если будет заинтересованность в алгоритме или потребуется адаптация отчета под ваши требования, то можете обратиться ко мне в личку. Автор - MCH
Дата добавления - 03.02.2016 в 01:49


= Мир MS Excel/Задача о рюкзаке - Мир MS Excel
Войти через uID
Войти через uID
В продолжении темы "Подбор слагаемых под нужную сумму" (сумма подмножеств)
Предлагаю решение "Задачи о рюкзаке"
Во вложении два алгоритма:
Первый подбирает предметы суммарным весом не более необходимого, имеющие максимальную стоимость.
Второй подбирает перечень предметов суммарным весом и стоимостью в определенном диапазоне от минимального до максимального.
В основе решения динамическое программирование, отсюда ограничения - работа с целыми числами, и существенное увеличение времени решения и количество выделяемой памяти от размеров рюкзака.
UPD 13/08/2015
Добавил решение классической "задачи о рюкзаке" жадным алгоритмом
Не всегда находит наилучшее решение, но работает достаточно быстро
В продолжении темы "Подбор слагаемых под нужную сумму" (сумма подмножеств)
Предлагаю решение "Задачи о рюкзаке"
Во вложении два алгоритма:
Первый подбирает предметы суммарным весом не более необходимого, имеющие максимальную стоимость.
Второй подбирает перечень предметов суммарным весом и стоимостью в определенном диапазоне от минимального до максимального.
В основе решения динамическое программирование, отсюда ограничения - работа с целыми числами, и существенное увеличение времени решения и количество выделяемой памяти от размеров рюкзака.
UPD 13/08/2015
Добавил решение классической "задачи о рюкзаке" жадным алгоритмом
Не всегда находит наилучшее решение, но работает достаточно быстро MCH
Во вложении два алгоритма:
Первый подбирает предметы суммарным весом не более необходимого, имеющие максимальную стоимость.
Второй подбирает перечень предметов суммарным весом и стоимостью в определенном диапазоне от минимального до максимального.
В основе решения динамическое программирование, отсюда ограничения - работа с целыми числами, и существенное увеличение времени решения и количество выделяемой памяти от размеров рюкзака.
UPD 13/08/2015
Добавил решение классической "задачи о рюкзаке" жадным алгоритмом
Не всегда находит наилучшее решение, но работает достаточно быстро Автор - MCH
Дата добавления - 12.08.2015 в 20:40
Читайте также:


