Задача распределения инвестиций в excel
Создадим модель для нахождения наилучшего распределения ресурсов, при котором минимизируются затраты, понесенные за несколько периодов (Allocation Problem). Расчет будем проводить с помощью надстройки Поиск решения.
Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .
Задача
Предприятие выпускает монопродукт (только один вид изделия и ничего более) и ему необходимо выполнить заказ клиента. Выпуск продукции осуществляется в течение 5 дней. Отгрузка заказа ежедневная. На предприятии 3 типа оборудования. Каждый тип оборудования выпускает один и тот же продукт. Производительность каждого типа оборудования разная. Каждый тип оборудования имеет постоянную и переменную часть расходов. Переменная часть расходов пропорциональна количеству произведенных изделий. Имеется ограниченное количество единиц оборудования каждого типа (но общее количество оборудования избыточно для выполнения заказа). Требуется минимизировать расходы на оборудование при условии выполнения заказа.
Создание модели
На рисунке ниже приведена модель, созданная для решения задачи (см. файл примера ).

Предприятие несет расходы в зависимости от типа оборудования: использование оборудования типа Alpha-3000 самое дорогое в эксплуатации, но оно и самое производительное. Оборудование типа Alpha-1000 самое дешевое в эксплуатации, но оно и менее производительное. Задача Поиска решения выбрать наиболее дешевое оборудование, так чтобы заказ был выполнен (мощностей Alpha-1000 не хватит для выполнения заказа). Казалось бы, решение очевидно (взять по максимуму дешевое оборудование, остальную производительность обеспечить более дорогим). Однако, если учесть, что из-за низкой производительности дешевых машин приходится их брать больше, неся существенные постоянные расходы, то решение уже не кажется очевидным.
Переменные (выделено зеленым) . В качестве переменных модели следует взять количество задействованных единиц оборудования каждого типа и суммарное количество продукции, выпущенное на каждом типе оборудования (производительность задается не для каждой единицы, а для типа в целом). Для наглядности диапазонам ячеек, содержащих переменные, присвоены имена Машин_Задействовано и Продукции_выпущено.
Ограничения (выделено синим) . Количество задействованных машин должно быть целым числом. Количество задействованных машин каждого типа должно быть не больше, чем имеется в наличии (используются именованные диапазоны Alpha XXXX _Задействовано и Alpha XXXX _в_наличии ). Всего должно быть выпущено продукции не меньше чем величина заказа (используется именованный диапазон Продукции выпущено_Итого ). В день возможно производить больше продукции, чем требуется в день заказа, излишек переносится на следующий день. Также необходимо ограничить производительность задействованного оборудования. Производительность задается не для каждой единицы, а для типа в целом (используются именованные диапазоны Продукции выпущено и Макс_производительность_задейств_машин ).
Целевая функция (выделено красным) . Целевая функция – это сумма операционных расходов за 5 дней. Операционные расходы, понесенные за день, задается формулой =СУММПРОИЗВ(B19:B21; Расходы_переменные)+ СУММПРОИЗВ(B13:B15; Расходы_постоянные) B19:B21 – количество продукции, выпущенной в определенный день. B13:B15 - количество задействованных машин в определенный день.
Это суммарные операционные расходы (переменная и постоянные части). Сумма операционных расходов за 5 дней должна быть минимизирована.

Убедитесь, что метод решения соответствует линейной задаче. Параметры Поиска решения были выбраны следующие:

Теперь в диалоговом окне можно нажать кнопку Найти решение .
Результаты расчетов
Поиск решения подберет оптимальный набор единиц оборудования по типам и их производительность, при котором операционные расходы будут минимальные, а заказ выполнен. В нашей задаче было установлено целочисленное ограничение, что существенно усложняет задачу поиска и, соответственно, сказывается на скорости расчета. Как показано на рисунке выше, Целочисленная оптимальность была выбрана 0% ( Целочисленная оптимальность (Integer Optimality) позволяет Поиску решения остановить поиск, в случае, если он найдет целочисленное решение, в пределах указанного процента от оптимального). В нашем случае (0%), требуется найти лучшее из известных Поиску решения решений. Поиск в этом случае занял 8 секунд, результат 23 311,50. Установив Целочисленную оптимальность 1%, поиск займет 0,2 сек, результат 23 370,50 (отличие на 0,3%). Это информация к размышлению: стоит ли увеличение точности на 0,3% уменьшения скорости расчетов более чем на порядок? Решать Вам. В любом случае, первые расчеты модели лучше проводить при Целочисленной оптимальности не равной 0%.
Пусть инвестиции в проект к концу первого года его реализации составят 20 000 руб. В последующие четыре года ожидаются годовые доходы по проекту: 6 000 руб., 8 200 руб., 12 600 руб., 18 800 руб.
Рассчитать чистую текущую стоимость проекта к началу первого года, если процентная ставка составляет 10% годовых .
Алгоритм решения задачи.
Чистая текущая стоимость проекта для периодических денежных потоков переменной величины рассчитывается с помощью функции ЧПС .
Так как по условию задачи инвестиция в сумме 20 000 руб. вносится к концу первого периода, то это значение следует включить в список аргументов функции ЧПС со знаком «минус» (инвестиционный денежный поток движется «от нас»). Остальные денежные потоки представляют собой доходы, поэтому при вычислениях укажем их со знаком «плюс».
Иллюстрация решения задачи представлена на рис. 4.7.
Чистая текущая стоимость проекта к началу первого года составляет:
= ЧПС (10%; -20000; 6000; 8200; 12600; 18800) = 13 216,9 3 руб.
Данный результат представляет собой чистую прибыль от вложения 20 тыс. руб. в проект с учетом покрытия всех расходов.

Рис. 4.7 . Фрагмент окна Excel с панелью функции ЧПС
При расчете чистой приведенной стоимости инвестиций с помощью функции ЧПС учитываются периодические платежи переменной величины как суммы ожидаемых расходов и доходов в каждый из периодов , дисконтированны е нормой процентной ставки , с использованием следующей формулы:

(4.8),
где: ЧПС – чистая текущая стоимость периодических выплат и поступлений;
Значение i – суммарный размер i -го денежного потока на конец периода (поступления – со знаком «плюс», выплаты – со знаком «минус»);
Ставка – норма дисконтирования за один период;
n – число периодов движения денежных потоков ( суммарное количество выплат и поступлений);
i – номер периода денежного потока.
Аналитический расчет задачи дает аналогичный результат:

Инвестор с целью инвестирования рассматривает 2 проекта, рассчитанных на 5 лет. Проекты характеризуются следующими данными:
- по 1-му проекту – начальные инвестиции составляют 550 тыс. руб., ожидаемые доходы за 5 лет соответственно 100, 190, 270, 300 и 350 тыс. руб.;
- по 2-му проекту – начальные инвестиции составляют 650 тыс. руб., ожидаемые доходы за 5 лет соответственно 150, 230, 470, 180 и 320 тыс. руб.
Определить, какой проект является наиболее привлекательным для инвестора при ставке банковского процента – 15% годовых .
Алгоритм решения задачи.
Оценку привлекательности проектов выполним с помощью показателя чистой текущей стоимости (функции ЧПС ).
Поскольку оба проекта предусматривают начальные инвестиции, вычтем их из результата , полученного с помощью функции ЧПС. ( Начальные инвестиции по проекту не нужно дисконтировать, так как они являются предварительными, уже совершенными к настоящему моменту времени).
Для облегчения анализа полученного решения исходные данные задачи представим в виде таблицы и в соответствующие ячейки введем значения формул с функциями ЧПС (рис. 4.8). В результате вычислений получим, что чистая приведенная стоимость инвестиций во второй проект почти на 22 тыс. руб. выше, чем в первый.


Непосредственное задание параметров в формулах расчета , как и вычисления с использованием формулы (4.8), да ю т те же ре зультаты.
Для первого проекта:
= ЧПС (15%; 100000; 190000; 270000; 300000; 350000) – 550000 = 203 691,03р.

Для второго проекта:
= ЧПС (15%; 150000; 230000; 470000; 180000; 320000) – 650000 = 225 392,59 р.

Таким образом, второй проект является для инвестора более привлекательным.
В некоторой степени функции ПС и ЧПС похожи. Сравнивая их, можно сделать следующие выводы :
1) в функции ПС периодические выплаты предполагаются одинаковыми, а в функции ЧПС они могут быть различными;
2) в функции ПС платежи и поступления происходят как в конце, так и в начале периода, а в функции ЧПС предполагается, что все выплаты производятся равномерно и всегда в конце периода.
Из последнего вывода следует, что если денежный взнос осуществляется в начале первого периода, то его значение следует исключить из аргументов функции ЧПС и добавить (вычесть, если это затраты) к результату функции ЧПС . Если же взнос приходится на конец первого периода, то его следует задать в виде отрицательного первого аргумента массива значений функции ЧПС .
Нельзя непосредственно оценивать эффективность, например, с помощью функции ЧПС , нескольких инвестиционных проектов, имеющих разную продолжительность. Предполагая, что допускается реинвестирование , необходимо свести полученные результаты чистой текущей стоимости по каждому из них к единому по продолжительности периоду. С этой целью можно воспользоваться специальными методами.
Метод цепного повтора предполагает оценку эффективности проектов в рамках общего одинакового срока их действия. Находится наименьшее общее кратное продолжительности проектов и рассчитывается, сколько раз каждый из них должен повториться. Затем определяется с учетом повторов и реинвестирования чистая приведенная стоимость каждого из проектов, которая и сравнивается. Большему значению соответствует более привлекательный проект.
Суммарная чистая приведенная стоимость повторяющегося потока для каждого из проектов находится по формуле:

(4.9),
где: ЧП С( n ) – чистая приведенная эффективность исходного проекта, найденная с учетом предварительных инвестиций;
n – длительность исходного проекта;
i – число повторов исходного проекта;
Ставка – норма дисконтирования за один период.
Метод бесконечного цепного повтора предполагает, что каждый из проектов может быть реализован неограниченное число раз.

(4.10)
Сравнить инвестиционную привлекательность двух проектов. Цена капитала составляет 10%. Предварительные инвестиции в первый проект составляют 100 млн. руб., во второй – 105 млн. руб. Продолжительность первого проекта – 2 года; доходы по годам – 50 и 70 млн. руб. соответственно. Продолжительность второго проекта – 3 года; доходы по годам – 34, 40 и 60 млн. руб. соответственно.
Алгоритм решения задачи.
Для решения задачи предварительно рассчитаем чистую приведенную стоимость проектов при их однократном выполнении, воспользовавшись функцией ЧПС и вычтя предварительные инвестиции. Затем, принимая во внимание разную продолжительность проектов, рассчитаем значения эффективности проектов по формулам (4.9) и (4.10).
При однократном выполнении проектов предпочтительным выходит второй проект ( ЧПС 1 = 3,306; ЧПС 2 = 4,046 ). Но такой вывод преждевременный (рис. 4.9).
Расчет эффективности проектов за 6 лет, а также при их бесконечном повторении дает результат полностью противоположный – более привлекательным является первый проект:
Создадим модель для нахождения наилучшего распределения ресурсов, при котором минимизируются затраты, понесенные за несколько периодов (Allocation Problem). В качестве ограничения используем требования к качеству продукции. Расчет будем проводить с помощью надстройки Поиск решения.
Задача оптимального распределения ресурсов (распределительная задача) заключается в отыскании наилучшего распределения ресурсов, при котором либо максимизируется результат, либо минимизируются затраты.
Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .
Задача
Примечание . Задача, в которой минимизируются затраты, понесенные в одном периоде решена в статье Поиск решения MS EXCEL (1.4). Распределение ресурсов (ограничение - требование к качеству продукции) , и имеет смысл предварительно познакомиться с изложенным там материалом.
Создание модели
На рисунке ниже приведена модель, созданная для решения задачи (см. файл примера ).


Переменные (выделено зеленым) . В качестве переменных модели следует взять бинарные значения (0 или 1), означающие 0 – карьер закрыт, 1 – открыт. Также необходимо варьировать количество известняка, выпускаемое каждым карьером, чтобы рассчитать содержание кальция и магния.
Ограничения (выделено синим) . Среднее содержание кальция и магния должно удовлетворять требования спецификации. Заказ должен быть выполнен. Объем выпущенной карьером продукции не должен превосходить его максимальной производительности.
Целевая функция (выделено красным) . Суммарные расходы за 5 лет на содержание открытых карьеров должны быть минимальны.

Примечание : для удобства настройки Поиска решения используются именованные диапазоны .
Для начала скажу, что я зарабатываю через вот этого брокера , проверен он временем! А вот хороший пример заработка , человек зарабатывает через интернет МНОГО МНОГО МНОГО и показывает все на примерах, переходи и читай! Добавь страницу в закладки. А теперь читаете информацию ниже и пишите свой отзыв
Видео: Поиск решения. Задача о выборе инвестиций
Чтобы познакомиться с мощным инструментом Excel Поиск решения, рассмотрим и решим с вами задачу.
Необходимо найти оптимальные объемы выпуска трех видов продукции для получения максимальной прибыли от их продажи.
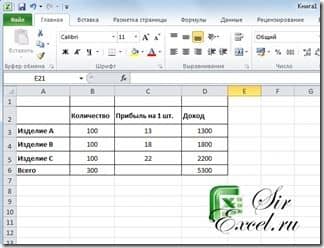
При решении данной задачи должны быть учтены следующие ограничения:
- общий объем производства – всего 300 изделий;
- должно быть произведено не менее 50 изделий А;
- должно быть произведено не менее 40 изделий В;
- должно быть произведено не более 40 изделий С.
- Внести в новый рабочий лист данные для вычисления прибыли от продажи трех видов продукции, причем в ячейки столбца D, и в ячейку B6 должны быть введены формулы.
- Запустить задачу поиска решений. Для этого: выполнить команду в Excel 2003 Сервис | Поиск решений … (В Excel 2007 и 2010 необходимо зайти в раздел Данные | Поиск решения)
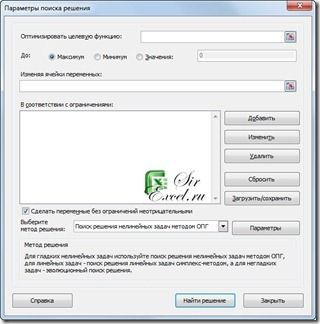
и в окне “Поиск решений” ввести данные:
Видео: Урок 1.Поиск решения, оптимизация, оптимальный план производства
- в поле «Установить целевую ячейку» указать адрес D6;
- установить флажок «Равной максимальному значению»;
- в поле «Изменяя ячейки» определить изменяемые ячейки (B3:B5);
- в поле «Ограничения» по одному добавить каждое из следующих четырех ограничений задачи (B6=300- B3>=50- B4>=40- B5<=40). Для этого щелкнуть по кнопке «Добавить» и в появившемся окне «Добавление ограничения» ввести ссылку на ячейку (B6), оператор ограничения (=) и значение (300), для добавления следующего ограничения щелкнуть кнопку «Добавить» и повторить процедуру добавления ограничения- после ввода последнего ограничения щелкнуть кнопку «ОК».
- в диалоговом окне «Поиск решения» щелкнуть кнопку “Выполнить”;
- в диалоге “Результаты поиска решения” установить переключатель «Сохранить найденное решение», в окне «Тип отчета» выбрать «Результаты» и нажать кнопку “Ok”;
В результате с помощью средства Поиск решения будут найдены оптимальные объемы выпуска продукции для максимизации прибыли.
Видео: Поиск решения. Задача о выпуске продукции
Очень надеемся, что наша статья помогла Вам. Будем благодарны, если Вы нажмете +1 и/или Мне нравится внизу данной статьи или поделитесь с друзьями с помощью кнопок расположенных ниже.
Читайте также:


