Решение задач нелинейного программирования excel

Обновлено: 22.01.2025

Решение задач нелинейного программирования в Excel в основном аналогично решению задач линейного программирования (см. подраздел 2.5).

Рассмотрим решение примера 6.3 средствами Excel.

Предположим, что желательно получить результаты (значения переменных X 1 и X 2 ) вячейках B2 и C2. В ячейке B3 введем формулу целевой функции:

В ячейке B4 введем формулу первого ограничения (на расход платины): =13*B2+6*C2

В ячейке D4 введем правую часть этого ограничения: 90.

Аналогично в ячейке B5 введем формулу ограничения на расход палладия (=8*B2+11*C2), в ячейке D5 – правую часть этого ограничения (88).

Укажем также некоторые поясняющие надписи и обозначения (хотя это и необязательно). Рабочий лист будет иметь примерно такой вид, как показано на рис.6.1.

Примечание . Значения 0 в ячейках B3-B5 получены автоматически для начальных значений переменных, равных нулю.

Для решения задачи из меню “Сервис” выберем элемент “Поиск решения”. В поле “Установить целевую ячейку” указывается ячейка B3, где находится формула целевой функции. Используя переключатели, необходимо указать, что требуется установить ячейку B3 “равной максимальному значению” (так как целевая функция в этой задаче подлежит максимизации). В поле “Изменяя ячейки” указываются ячейки, в которых должны находиться значения переменных: B2:C2.

В области “Ограничения” указываются ограничения, как показано в подразделе 2.5. Необходимо ввести ограничения на расход платины и палладия, заданные на рабочем листе, а также ограничение на неотрицательность всех переменных (B2:C2>=0) и ограничение на их целочисленность (в поле “Ссылка на ячейку” указать B2:C2, а в поле знака ограничения выбрать отметку “цел”).

Для решения задачи следует нажать кнопку “Выполнить”. Рабочий лист с результатами решения показан на рис.6.2.

Рис.6.1. Рабочий лист Excel для решения

Рис.6.2. Рабочий лист Excel с результатами

решения примера 6.3

В ячейках B2 и C2 получены оптимальные значения переменных, в ячейке B3 – оптимальное значение целевой функции. Эти величины совпадают с результатами, полученными по методу Франка-Вульфа.

В ячейках B4 и B5 находятся значения левых частей ограничений. Видно, что на выпуск изделий будет израсходовано 90 г платины и 70 г палладия.

1. В табличном процессоре Excel для решения задач оптимизации (элемент меню “Поиск решения”) используются именно градиентные методы.

Задачи программирования становятся нелинейными, когда в них появляются произведения, обратные величины или высшие порядки нескольких или всех переменных.

Задачи нелинейного программирования имеют более важное значение, чем линейные задачи, потому что они чаще встречаются на практике. Иногда можно упростить нелинейную задачу, делая ряд приближенных допущении, так, чтобы она формулировалась в линейной постановке. Так, например, симплекс-метод и метод наискорейшего спуска, рассмотренные выше, не могут быть применимы в случае нелинейных ограничений и нелинейной целевой функции. В этом случае, используя итерационные процессы, задача сначала линеаризуется для небольшого интервала, так что новое решение получается из результатов предыдущего.

Однако это приближение неприемлемо для реальных задач и часто не отражает ее важных особенностей. Например, в случае невыпуклых задач, где встречается более одного локального экстремума, линейная постановка может привести к тому, что будет найден только один из локальных экстремумов, при этом часто теряется глобальный экстремум.

Нелинейные задачи оптимального проектирования строительных конструкций разделяются на две основные группы:

1) задачи безусловной оптимизации, в которых на управляемые переменные (х₁, х₂, . х_n), которым соответствует минимальное значение целевой функции F (х₁, х₂, . х_n), не накладывается никаких ограничений;

2) задачи условной оптимизации, в которых на управляемые переменные (х₁, х₂, . х_n), которым соответствует минимальное значение целевой функции F (х₁, х₂, . х_n), накладываются ограничения, задаваемые в виде равенств и неравенств.

Считается, что большинство задач проектирования безусловной оптимизации проще, чем задачи условной оптимизации. Поэтому, одним из способов решения задачи условной оптимизации является ее преобразование к задаче безусловной оптимизации.

Методы решения задач безусловной оптимизации можно разделить на две группы:

1) методы прямого поиска, в которых вычисляются только значения целевой функции;

2) градиентные методы, в которых используются значения производных целевой функции.

Рассмотрим несколько методов решения задач нелинейного программирования.

Метод прямого поиска

Суть метода прямого поиска состоит в следующем. Принимается какое-либо начальное значение целевой функции. Затем все переменные фиксируются, кроме одной, например, х₁. Значение х₁ изменяется до тех пор, пока функция убывает. Как только функция перестает убывать значение х₁ фиксируют и запоминают последнее значение целевой функции. Далее цикл повторяется, но уже изменяется следующая переменная, например, х₂. Другие переменные сохраняют постоянное значение. Цикл повторяется с каждым переменным до тех пор, пока не будет достигнут оптимум целевой функции. Об этом будет свидетельствовать то, что всякое изменение любого аргумента в сторону увеличения приведет к возрастанию целевой функции.

Метод прямого поиска позволяют получить решение задачи на основе использования только значений целевой функции. Важность этих методов несомненна, поскольку в ряде практических инженерных задач информация о значениях целевой функции является единственной надежной информацией, которой располагает исследователь. Но при использовании даже самых эффективных прямых методов для получения решения иногда требуется очень большое количество вычислений значений функции. Поэтому в задачах, где целевые функции непрерывны и дифференцируемы, есть необходимость применения градиентных методов, которые быстрее сходятся к оптимальной точке, чем методы прямого поиска.

Градиентные методы

Ряд инженерных задач связан с оптимизацией при наличии некоторого количества ограничений на управляемые переменные. Такие ограничения существенно уменьшают размеры области, в которой проводится поиск оптимума. Может показаться, что уменьшение размеров допустимой области должно упростить поиск. На самом деле, процесс оптимизации становится более сложным, поскольку установленные критерии оптимальности нельзя использовать при наличии ограничений.

Градиентные методы минимизации целевой функции заключается в движении от точки х_k к точке х_k₊₁ в направлении антиградиента. Градиент функции определяется как вектор – столбец из частных производных

Движение из точки х_k в направлении антиградиента в следующую точку х_k₊₁ осуществляется по следующей схеме

Метод штрафных функций

Метод штрафных функций используется при решении задач, для которых оптимизация целевой функции при наличии ограничений является более трудоемкой, чем без ограничений. Однако в этом случае ограничения в виде функции «штрафа» добавляются к целевой функции.

По методу штрафных функций задача сводится к минимизации другой функции

С помощью штрафной функции исходная задача условной оптимизации преобразуется в последовательность задач безусловной оптимизации. Методы преобразования определяются видом штрафной функции, а также правилами, по которым производится пересчет штрафных параметров по окончании очередного цикла безусловной оптимизации.

Методы штрафных функций классифицируются в соответствии со способами учета ограничений-неравенств. Но в любом случае, штрафная функция задается так, чтобы допустимые точки задачи имели преимущество перед недопустимыми в отношении безусловной оптимизации штрафной функции.

Рассмотрим некоторые типы штрафов.

Квадратичный штраф используется для учета ограничений - равенств и определяется выражением:

При минимизации этот штраф препятствует отклонению величины f_i (x) от нуля (как в сторону положительных, так и в сторону отрицательных значений).

Логарифмический штраф. Другим широко используемым типом штрафа является логарифмический штраф, который определяется выражением:

Этот штраф положителен при всех x, таких, что 0 < f_i (x) < 1, и отрицателен при f_i (x) > 1. В данном случае вводится искусственная дискриминация точек допустимой области: внутренним точкам отдается предпочтение перед граничными.

Пример. Найти минимум функции F(x) = (x₁-6) 2 + (x₂-8) 2 (167)

Используя метод штрафных функций, определим аналитическим путем точку минимума.

Штрафная функция имеет вид (164)

Условия стационарности принимают вид

Откуда следует, что x₁ = x₂ – 2. (172)

в котором один из корней дает координату стационарной точки

Второй корень соответствует недопустимой точке и должен быть отброшен.

Учитывая (172), определяем первое неизвестное

Подставим значения неизвестных x₁, x₂ в выражение исходной функции (167) и определим ее минимум

F(x)_min = (x₁-6) 2 + (x₂-8) 2 = (1,5 – 4) 2 +(3,5 – 4) 2 = 92,5 (178)

Получено точное решение. Однако, получить точное решение удается не всегда и требуется численное решение с использованием алгоритма метода штрафных функций [1].

Решение задачи нелинейного программирования отличается от решения задачи линейного программирования следующим:

назначаются начальные значения искомых переменных;

в диалоговом окне Параметры поиска решения не надо вводить Линейная модель.

Начальные значения желательно назначать близкими к ожидаемым оптимальным значениям, что ускорит решение задачи (часто их принимаются равными единице). Обязательное требование заключается в том, чтобы целевая функция в начальной точке не была равной нулю.

Решение задачи НЛП в Excel рассмотрим на следующих примерах:

Пример 1. Минимизировать

Создадим форму для ввода условий задачи (рис. 2.1) и введем:

зависимости для целевой функции и ограничений;

начальные значения переменных, равные единице;

правые части ограничений.

Сервис, Поиск решения…

На экране: диалоговое окно Поиск решения (рис. 2.2).

целевую функцию С9; минимизировать;

изменяемые ячейки В3:D3;

ограничения С10 = Е10; С11 = Е11.

Перейдем к решению задачи. Выполнить.

На экране: результат решения (рис. 2.3).

После успешного завершения поиска решения на экране появляется диалоговое окно Результаты поиска решения. С помощью этого диалогового окна можно вызвать отчеты трех типов:

Среди них только Отчет по устойчивости (рис. 2.4) отличается от аналогичных результатов для задачи линейного программирования.

Отчет по устойчивости состоит из двух таблиц.

В таблице 1 приводятся значения для переменных:

результат решения задачи;

нормированный градиент – величина, приводимая при выборе некоторых методов в диалоговом окне Параметры поиска решения.

В таблице 2 приводятся значения для ограничений:

величина правых левой части каждого ограничения (2 и 5 соответственно);

множитель Лагранжа – аналог двойственной оценки в задаче линейного программирования, который показывает, как изменится целевая функция при изменении правой части ограничения на единицу.

Если решается задача НЛП с ограничениями – неравенствами следует при введении зависимостей по ограничениям ввести соответствующие знаки.

Пример 2. Минимизировать

На листе Excel создадим форму, в которую введем исходные данные и формулы, определяющие зависимости (рис. 2.5).

На рис. 22 - 25 и табл. 9 отражена последовательность действий, необходимая для получения решения задачи.

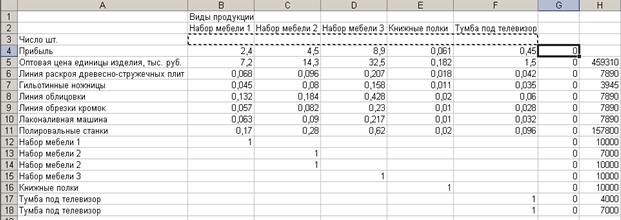
Рис. 22. Рабочий лист Excel с введенными данными

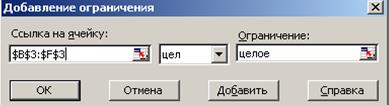
Рис. 23. Введение ограничений целочисленности переменных

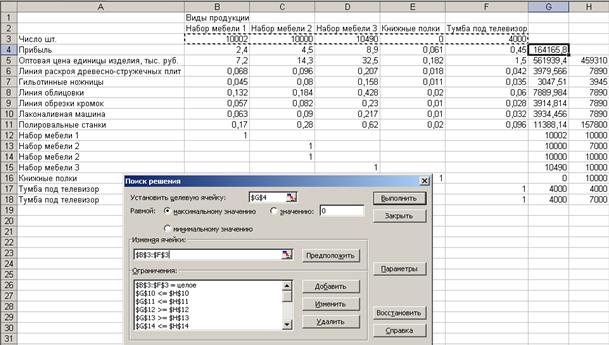
Рис. 24. Введены все условия для решения задачи

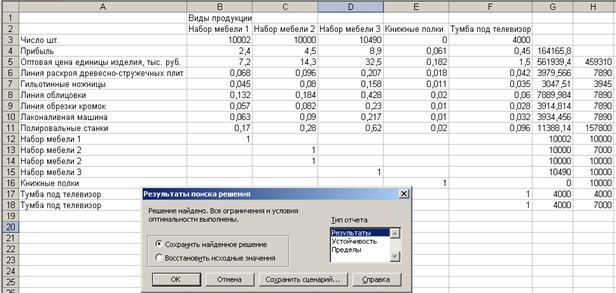
Рис. 25. Решение найдено. Все ограничения и условия оптимальности выполнены

Таблица 9 Результаты применения надстройки Поиск решений

Виды продукции
Набор мебели	Книжные полки	Тумба под телевизор
Количество, шт.	10 000
Прибыль	2,4	4,5	8,9	0,061	0,45
Ограничения (часть)	Левая	Правая
Оптовая цена единицы изделия, тыс. руб.	7,2	14,3	26,9	0,243	1,5
Линия раскроя древесностружечных плит	7889,98	0,068	0,096	0,207	0,018	0,042
Гильотинные ножницы	3047,51	0,045	0,080	0,158	0,011	0,035
Линия облицовки	7889,98	0,132	0,184	0,428	0,020	0,060
Линия обрезки кромок	3914,81	0,057	0,082	0,230	0,010	0,028
Лаконаливная машина	3934,46	0,063	0,090	0,217	0,010	0,032
Полировальные станки	11388,1	0,170	0,280	0,620	0,020	0,096
Набор мебели 1
Набор мебели 2
Набор мебели 2
Набор мебели 3
Книжные полки
Тумба под телевизор
Тумба под телевизор

Ответ. Для получения максимальной прибыли необходимо произвести:

Читайте также: