Решение задач линейного программирования в excel
Ранее я писал, что для принятия решений с учетом ограничивающих факторов может использоваться линейное программирование. Напомню, что этот метод решает проблему распределения ограниченных ресурсов между конкурирующими видами деятельности с тем, чтобы максимизировать или минимизировать некоторые численные величины, такие как маржинальная прибыль или расходы.
При решении задач линейного программирования, во-первых, необходимо составить модель, то есть сформулировать условия на математическом языке. После этого решение может быть найдено графически (см., например, здесь), с использованием надстройки Excel «Поиск решения» (рассмотрено в настоящей заметке) или с помощью специализированных компьютерных программ (см., например, здесь).
Рассмотрим линейное программирование в Excel на примере задачи, ранее решенной графическим методом.
Задача. Николай Кузнецов управляет небольшим механическим заводом. В будущем месяце он планирует изготавливать два продукта (А и В), по которым удельная маржинальная прибыль оценивается в 2500 и 3500 руб., соответственно. Изготовление обоих продуктов требует затрат на машинную обработку, сырье и труд. На изготовление каждой единицы продукта А отводится 3 часа машинной обработки, 16 единиц сырья и 6 единиц труда. Соответствующие требования к единице продукта В составляют 10, 4 и 6. Николай прогнозирует, что в следующем месяце он может предоставить 330 часов машинной обработки, 400 единиц сырья и 240 единиц труда. Технология производственного процесса такова, что не менее 12 единиц продукта В необходимо изготавливать в каждый конкретный месяц. Необходимо определить количество единиц продуктов А и В, которые Николай доложен производить в следующем месяце для максимизации маржинальной прибыли.
1. Воспользуемся математической моделью построенной в упомянутой заметке. Вот эта модель:
Максимизировать: Z = 2500 * х1 + 3500 *х2
При условии, что: 3 * х1 + 10 * х2 ≤ 330
2. Создадим экранную форму и введем в нее исходные данные (рис. 1).
Рис. 1. Экранная форма для ввода данных задачи линейного программирования
Обратите внимание на формулу в ячейке С7. Это формула целевой функции. Аналогично, в ячейки С16:С18 введены формулы для расчета левой части ограничений.
3. Проверьте, если у вас установлена надстройка «Поиск решения» (рис. 2), пропустите этот пункт.
Рис. 2. Надстройка Поиск решения установлена; вкладка «Данные», группа «Анализ»
Если надстройки «Поиск решения» вы на ленте Excel не обнаружили, щелкните на кнопку Microsoft Office, а затем Параметры Excel (рис. 3).
Рис. 3. Параметры Excel
Выберите строку Надстройки, а затем в самом низу окна «Управление надстройками Microsoft Excel» выберите «Перейти» (рис. 4).
Рис. 4. Надстройки Excel
Рис. 5. Активация надстройки «Поиск решения»
После загрузки надстройки для поиска решения в группе Анализ на вкладке Данные становится доступна команда Поиск решения (рис. 2).
4. Следующим этапом заполняем окно Excel «Поиск решения» (рис. 6)
Рис. 6. Заполнение окна «Поиск решения»
В поле «Установить целевую ячейку» выбираем ячейку со значением целевой функции – $C$7. Выбираем, максимизировать или минимизировать целевую функцию. В поле «Изменяя ячейки» выбираем ячейки со значениями искомых переменных $C$4:$D$4 (пока в них нули или пусто). В области «Ограничения» с помощью кнопки «Добавить» размещаем все ограничения нашей модели. Жмем «Выполнить». В появившемся окне «Результат поиска решения» выбираем все три типа отчета (рис. 7) и жмем Ok. Эти отчеты нужны для анализа полученного решения. Подробнее о данных, представленных в отчетах, можно почитать здесь.
Рис. 7. Выбор типов отчета
На основном листе появились значения максимизированной целевой функции – 130 000 руб. и изменяемых параметров х1 = 10 и х2 = 30. Таким образом, для максимизации маржинального дохода Николаю в следующем месяце следует произвести 10 единиц продукта А и 30 единиц продукта В.
Если вместо окна «Результат поиска решения» появилось что-то иное, Excel`ю найти решение не удалось. Проверьте правильность заполнения окна «Поиск решения». И еще одна маленькая хитрость. Попробуйте уменьшить точность поиска решения. Для этого в окне «Поиск решения» щелкните на Параметры (рис. 8.) и увеличьте погрешность вычисления, например, до 0,001. Иногда из-за высокой точности Excel не успевает за 100 итераций найти решение. Подробнее о параметрах поиска решения можно почитать здесь.
В Excel 2007 для включения пакета анализа надо нажать перейти в блок Параметры Excel, нажав кнопку в левом верхнем углу, а затем кнопку «Параметры Excel» внизу окна:

Далее в открывшемся списке нужно выбрать Надстройки, затем установить курсор на пункт Поиск решения, нажать кнопку Перейти и в следующем окне включить пакет анализа.
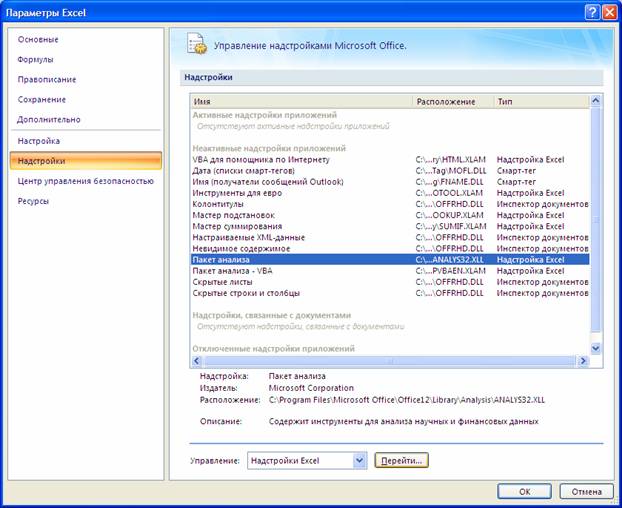
Для того чтобы решить задачу ЛП в табличном процессоре Microsoft Excel , необходимо выполнить следующие действия:
1. Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
· переменных,
· целевой функции (ЦФ),
· ограничений,
· граничных условий;
b) ввести исходные данные в экранную форму:
· коэффициенты ЦФ,
· коэффициенты при переменных в ограничениях,
· правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
· формулу для расчета ЦФ,
· формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне "Поиск решения" ):
· целевую ячейку,
· направление оптимизации ЦФ;
e) ввести ограничения и граничные условия (в окне "Поиск решения" ):
· ячейки со значениями переменных,
· граничные условия для допустимых значений переменных,
· соотношения между правыми и левыми частями ограничений.
2. Решить задачу:
a) установить параметры решения задачи (в окне "Поиск решения" );
b) запустить задачу на решение (в окне "Поиск решения" );
c) выбрать формат вывода решения (в окне "Результаты поиска решения" ).
Рассмотрим подробно использование MS Excel на примере решения следующей задачи.
Фабрика "GRM pic" выпускает два вида каш для завтрака - "Crunchy" и "Chewy". Используемые для производства обоих продуктов ингредиенты в основном одинаковы и, как правило, не являются дефицитными. Основным ограничением, накладываемым на объем выпуска, является наличие фонда рабочего времени в каждом из трех цехов фабрики.
Управляющему производством Джою Дисону необходимо разработать план производства на месяц. В приведенной ниже таблице указаны общий фонд рабочего времени и число человеко-часов, требуемое для производства 1 т продукта.
Цех | Необходимый фонд рабочего времени чел.-ч/т | Общий фонд рабочего времени чел.-ч. в месяц | |
"Crunchy" | "Chewy" | ||
| А. Производство | 10 | 4 | 1000 |
| В. Добавка приправ | 3 | 2 | 360 |
| С. Упаковка | 2 | 5 | 600 |
а) Сформулировать модель линейного программирования, максимизирующую общий доход фабрики за месяц.
б) Решить ее c помощью MS Excel.
Ввод исходных данных
Создание экранной формы и ввод исходных данных
Экранная форма для решения в MS Excel представлена на рисунке 1.
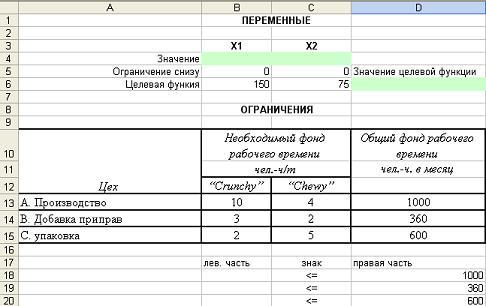
В экранной форме на рисунке 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка на листе Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП. Так, например, переменным задачи 1 соответствуют ячейки B4 (x1), C4 (x2), коэффициентам ЦФ соответствуют ячейки B6 (c1=150), C6 (c2=75), правым частям ограничений соответствуют ячейки D18 (b1=1000), D19 (b2=360), D20 (b3=600) и т.д.
Ввод зависимостей из формальной постановки задачи в экранную форму
Для ввода зависимостей определяющих выражение для целевой функции и ограничений используется функция MS Excel СУММПРОИЗВ , которая вычисляет сумму попарных произведений двух или более массивов.
Одним из самых простых способов определения функций в MS Excel является использование режима "Вставка функций" , который можно вызвать из меню "Вставка" или при нажатии кнопки fx (рисунок 2) на стандартной панели инструментов.
Рисунок 2
Так, например, выражение для целевой функции из задачи 1 определяется следующим образом:
· курсор в поле D6;
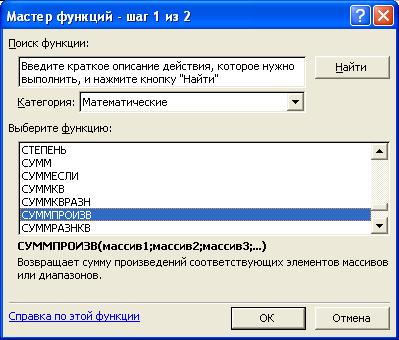
· нажав кнопку fx , вызовите окно "Мастер функций - шаг 1 из 2";
· выберите в окне "Категория" категорию "Математические";
· в окне "Функция" выберите функцию СУММПРОИЗВ (рис. 3);
Рисунок 3
· в появившемся окне "СУММПРОИЗВ" в строку "Массив 1" введите выражение B$4:C$4 , а в строку "Массив 2" - выражение B6:C6 (рис. 4);
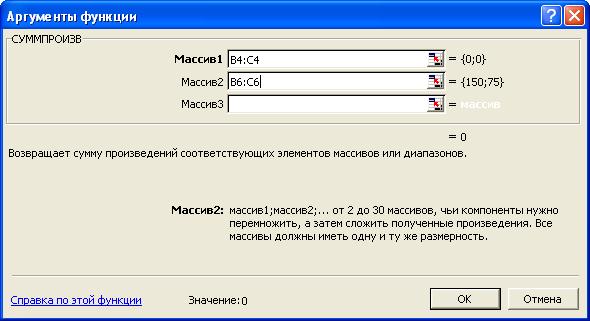
Левые части ограничений задачи (1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи ( B3, C3 ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения ( B13, C13 - 1-е ограничение; B14, С14 - 2-е ограничение и B15, С15 - 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл.1.
Таблица 1.
Формулы, описывающие ограничения модели (1)
| Левая часть ограничения | Формула Excel |
| 10x1+4x2 или B3×B13+C3×C13 | =СУММПРОИЗВ(B4:C4;B13:C13)) |
| 3x1+2x2 или B3×B14+C3×C14 | =СУММПРОИЗВ(B4:C4;B14:C14)) |
| 2x1+5x2 или B3×B15+C3×C15 | =СУММПРОИЗВ(B4:C4;B15:C15) |
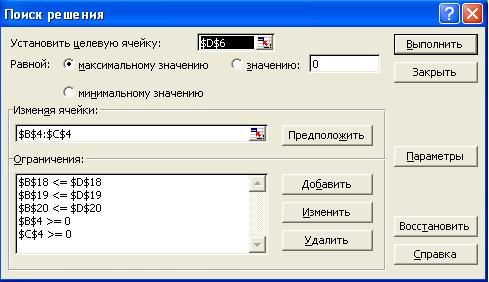
Дальнейшие действия производятся в окне "Поиск решения" , которое вызывается из меню "Сервис" (рис.5):
· поставьте курсор в поле "Установить целевую ячейку" ;
· введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке "максимальному значению".
Ввод ограничений и граничных условий
Задание ячеек переменных
В окно "Поиск решения" в поле "Изменяя ячейки" впишите адреса $B$4:$С$4 . Необходимые адреса можно вносить в поле "Изменяя ячейки" и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
Задание граничных условий для допустимых значений переменных
Окно "Поиск решения" после ввода всех необходимых данных задачи (1) представлено на рис. 5.
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки "Изменить" или "Удалить" (см. рис. 5).
Решение задачи
Установка параметров решения задачи
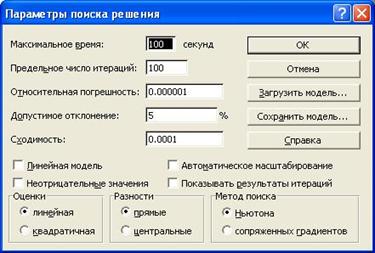
Задача запускается на решение в окне "Поиск решения" . Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку "Параметры" и заполнить некоторые поля окна "Параметры поиска решения" (рис. 7).
Рис. 7 - Параметры поиска решения, подходящие для большинства задач ЛП
Параметр "Максимальное время" служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр "Предельное число итераций" служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр "Относительная погрешность" служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр "Допустимое отклонение" служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр "Сходимость" применяется только при решении нелинейных задач.Установка флажка "Линейная модель" обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки "OK" .
Запуск задачи на решение
Запуск задачи на решение производится из окна "Поиск решения" путем нажатия кнопки "Выполнить" .
Читайте также:


