Решение 23 задания егэ информатика эксель
В данном курсе разобраны ВСЕ задачи КЕГЭ по информатике , которые могут быть решены в в электронных таблицах (Excel). Приведены неожиданные и очень эффективные способы решения в Excel некоторых заданий ЕГЭ. Разобраны все нюансы и хитрости решения задач ЕГЭ по информатике в Excel. Также разобраны необходимые для решения задач основы и продвинутые возможности Excel. Разобрана необходимая теория для решения задач.
В курсе подробно разобраны решения задач в Excel:
2, 3, 5, 9, 12, 16, 17, 18, 23, 15(некоторые типы задач)
Результатом прохождения данного курса является:
- овладение эффективными способами решения 14 из 27 задач КЕГЭ по информатике
- Изучение основ и некоторых продвинутых возможностей работы в Excel:
- Изучите основы Excel (адресация, формулы, автозаполнение)
- Научитесь пользоваться встроенными функциями Excel (математическими, логическими, функции по работе с тестом, массивами и т.д.)
- Научитесь работать с числами в разных системах счисления в Excel
- Реализуете переборные алгоритмы в Excel
- Научитесь работать со строками в Excel
- Научитесь работать с массивами в Excel
- Изучение необходимой теории для решения задач КЕГЭ по информатике
Преимущества курса:
1) Преподаватели с большим опытом
Полная теория, алгоритмы, способы решения задач, что обеспечит системные знания от учителя информатики высшей категории, работающего в профильных инф-мат классах, подготовившего за последние 3 года СЕМЬ стобальников из 43 учащихся, при среднем балле - 93,2, а также большое кол-во призёров и победителей олимпиад по программированию Всероссийского и других уровней. Преподаватель владеет всеми олимпиадными алгоритмами, что необходимо для решения сложных задач ЕГЭ.
Лайфхаки и секретные способы решения задач от выпускника - преподавателя курса, сдавшего КЕГЭ в 2021 на 98 баллов, а также призера олимпиад по программированию.
2) Мобильность
Курс будет обновляться по мере появления новых типов задач.
3) Обратная связь
Работая с курсом вы можете построить свою образовательную траекторию.
На все вопросы учащихся будут даваться ответы преподавателей.
Для кого этот курс
Подготовка к ЕГЭ по информатике; учащиеся школ с 5 по 11 класс; все, кто интересуются информатикой; все, кто интересуются Excel
Проверяемые элементы содержания: Умение анализировать результат исполнения алгоритма
"Один из распространенных способов выполнения этого задания – выписать последовательность
рекуррентных формул, определяющих, сколькими способами можно получить текущее число из ближайших предшественников, одновременно производя вычисления по этим формулам. «Ближайших» в данном случае означает тех, из которых текущее число получается в результате применения программы, состоящей из одной команды. Когда текущее число сравняется с заданным, количество таких способов и будет искомым числом программ"
Типичные ошибки и рекомендации по их предотвращению:
"Не стоит пытаться перечислить все пути в явном виде, это слишком трудоёмко и, скорее всего, в итоге приведёт к ошибке. Распространённая ошибка – экзаменуемые в процессе рекуррентных вычислений забывают о том, что траектория обязана содержать или не содержать указанные в условии числа"
ФГБНУ "Федеральный институт педагогических измерений"Более подробное знакомство с динамическим программированием доступно по ссылке.
Решение 23 заданий ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Исполнитель преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
Сколько существует программ, для которых при исходном числе 3 результатом является число 37 и при этом траектория вычислений содержит число 18?
Результат: 28
Подробный разбор смотрите на видео:
Исполнитель Счетчик преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
Сколько существует программ, для которых при исходном числе 5 результатом является число 250, и при этом траектория вычислений содержит число 35 и не содержит числа 105?
- Так как общая траектория 5 -> 250 содержит в себе и те отрезки, которые должны быть удалены (содержащие 105), то разобьем ее на несколько отрезков, отображенных на луче:


Пояснение: поскольку это задача динамического программирования, то полученные в начале результаты, используются для дальнейших вычислений:
Результат: 5
Результат: 1

Результат: 1
Результат: 8
23.2: Разбор 23 (22) задания ЕГЭ по информатике 2017 года ФИПИ вариант 15 (Крылов С.С., Чуркина Т.Е.):У исполнителя Увеличитель две команды, которым присвоены номера:
Первая из них увеличивает число на экране на 1, вторая умножает его на 4.
Программа для Увеличителя – это последовательность команд.
Сколько есть программ, которые число 3 преобразуют в число 44?
- Возьмем такое наименьшее число, находящееся в интервале от 3 до 44, для которого применима только одна команда:
- Отобразим число 12 на графе, указав и саму команду и результат. То есть для 12 можно использовать только одну команду (12 + 1 = 13):
Пояснение: Красным цветом будем выделять количество команд для получения конкретного числа, а в круг обводить итоговое суммарное количество команд.

Пояснение: поскольку это задача динамического программирования, то полученные промежуточные результаты, используются для дальнейших вычислений:
- для 11 взят результат, полученный для 12 (1);
- для 10 взят результат, полученный для числа 11 (2);
- для 9 взят результат, полученный для 10 (3);
- и т.д.
Результат: 10
Предлагаем посмотреть видео с решением данного 23 задания:
23.3: 23 (22) задание. Демоверсия ЕГЭ 2018 информатика:Исполнитель М17 преобразует число, записанное на экране.
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 3
Первая из них увеличивает число на экране на 1, вторая увеличивает его на 2, третья умножает на 3. Программа для исполнителя М17 – это последовательность команд.
Сколько существует таких программ, которые преобразуют исходное число 2 в число 12 и при этом траектория вычислений программы содержит числа 8 и 10? Траектория должна содержать оба указанных числа.
В 2021 году экзамен по информатике кардинально изменился. Теперь он проходит в компьютерной форме. Полностью исчезли задания, требующие простого воспроизведения формул и терминов. В ЕГЭ нового типа нужно рассуждать и решать задачи. Часть выполняется на бумаге, в электронную форму вносится только ответ. Другая часть представляет собой работу в компьютерных программах. Изменения коснулись и номера 23 из ЕГЭ по информатике. Раньше это была задача на системы логических уравнений, которая вызывала у школьников затруднения. В нынешнем году ее убрали, заменив на вопрос с анализом результата исполнения алгоритма. Он относится к первой части и дает 1 балл. Разбираемся в теории и решении 23 задания в ЕГЭ по информатике.
Теория
Задача 23 связана с алгоритмами. Алгоритм — полное и точное описание действий, приводящее к конечному результату. В информатике исходными и выходными данными является информация. Алгоритмы реализуются в компьютерных программах, они должны занимать определенный объем памяти и время. Алгоритм должен быть:

- дискретным (прерывным). Состоит из последовательности простых шагов;
- детерминированным (определенным). В описании операций нет многозначности, исполнитель понимает их и может реализовать;
- массовым. Позволяет решить не одну задачу, а группу аналогичных. В качестве возможных данных используются переменные;
- результативным. Рассматривает все ситуации, дает конечный результат;
- конечным. Имеется определенное количество шагов;
- эффективным. Время выполнения алгоритма позволяет использовать его для реальных задач.
Алгоритм делят на базовые элементы (структуры). Структуры бывают трех типов: следование (последовательные действия), ветвление (программа проверяет условие и выбирает один из вариантов действия в зависимости от результата), цикл (несколько действий повторяются многократно). В задании 23 по информатике используются следующие способы записи алгоритмов:
- обычный язык. Текст с разделением на шаги;
- блок-схема. Программа представляется графически, используются специальные блоки:
Ввод, вывод данных
Цикл с параметром
Обращение к дополнительным алгоритмам
- Блок
- Обозначение
- Начало, конец
- Ввод, вывод данных
- Операция
- Условие
- Цикл с параметром
- Обращение к дополнительным алгоритмам
- языки программирования. Имеют строгие правила записи, включающие в себя символы и зашифрованные слова;
- псевдокод. Объединение обычного языка и языка программирования. Нет строгих правил, но есть неизменяемые слова, задающие алгоритм. Например, «нач» — начало, «кон» — конец, «рез» — результат.
Примеры из ЕГЭ
Чтобы хорошо подготовиться к экзамену, нужно решить практические задачи по 23 заданию. Номер основан на динамическом программировании — решении сложных задач путем приведения к более простым. То есть, для выполнения конечного алгоритма нужно разобраться с подзадачами.
Для решения могут применяться графический и табличный способ.
Пример 1. У исполнителя Удвоитель две команды:
2. умножить на 2
Программа для Удвоителя — последовательность команд.
Сколько есть программ, преобразующих число 1 в 25?
Решение. Решим графическим способом. Начнем выполнять с конца. Итоговый результат получается двумя способами — прибавлением к числу Х тройки или умножением числа Y на 2. 25 — нечетное число, вариант с умножением отпадает. Следовательно, перед 25 в алгоритме стояло 25-3=22.
Число 22 получается и умножением, и сложением. Алгоритм разделяется на 2: в одном число 22:2=11, а в другом 22-3=19. Каждое из этих чисел анализируем по той же схеме. Нужно «разворачивать» алгоритм до тех пор, пока каждая из ветвей не закончится единицей. Рисунок выглядит так:

Пример 2. Исполнитель Вычислитель преобразует число, записанное на экране. У исполнителя есть две команды:
2. умножить на 2
Сколько существует программ, преобразующих исходное число 2 в число 9?
Решение. Воспользуемся таблицей. В этом случае решаем в прямом порядке. В первой строке таблицы записываем все целые числа от исходного до итогового. Во второй пишем число, к которому нужно прибавить 1 для получения цифры из первой строки. В третьей строке аналогично, но с умножением. Четвертая строка — количество разных команд, которые могут привести к получению числа.
В ячейки электронной таблицы записаны числа, как показано на рисунке:
В ячейку A4 записали формулу =$D2+E$2. Затем ячейку A4 скопировали в одну из ячеек диапазона A1:B6, после чего в этой ячейке появилось числовое значение 6002. В какую ячейку выполнялось копирование?
Примечание: знак $ обозначает абсолютную адресацию.
Заметим, что после копирования формулы из ячейки A4 в одну из ячеек диапазона A1:B6 результатом стала сумма двух слагаемых, у которых последней цифрой является единица. Следовательно, формулу из ячейки А4 скопировали в одну из ячеек диапазона B1:B6, поскольку при копировании формулы из ячейки A4 в одну из ячеек диапазона A1:A6 одним из слагаемых будет значение ячейки E2, которое в сумме с каким-либо из других значений таблицы не даст числа 6002. Следовательно, одним из слагаемых является ячейка F2.
Осталось найти второе слагаемое, которое должно равняться 4001. Следовательно, другим слагаемым является ячейка D4. Чтобы получить формулу =$D4+F$2, нужно скопировать формулу из ячейки A4 в ячейку B6.
В ячейки электронной таблицы записаны числа, как показано на рисунке:
В ячейку B3 записали формулу =$D4+E$4. Затем ячейку B3 скопировали в одну из ячеек диапазона A1:B6, после чего в этой ячейке появилось числовое значение 6002. В какую ячейку выполнялось копирование?
Примечание: знак $ обозначает абсолютную адресацию.
Заметим, что после копирования формулы из ячейки B3 в одну из ячеек диапазона A1:B6 результатом стала сумма двух слагаемых, у которых последней цифрой является единица. Следовательно, формулу из ячейки B3 скопировали в одну из ячеек диапазона A1:A6, поскольку при копировании формулы из ячейки B3 в одну из ячеек диапазона B1:B6 одним из слагаемых будет значение ячейки E4, которое в сумме с каким-либо из других значений таблицы не даст числа 6002. Следовательно, одним из слагаемых является ячейка D4.
Осталось найти второе слагаемое, которое должно равняться 2001. Следовательно, другим слагаемым является ячейка D2. Чтобы получить формулу =$D2+D$4, нужно скопировать формулу из ячейки B3 в ячейку A1.
В ячейки электронной таблицы записаны числа, как показано ниже:
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 10 | 20 | 30 | 40 | 50 | 60 |
| 2 | 70 | 80 | 90 | 100 | 200 | 300 |
| 3 | 400 | 500 | 600 | 700 | 800 | 900 |
| 4 | 1200 | 1400 | 1600 | 1800 | 2000 | 2200 |
| 5 | ||||||
| 6 |
В ячейку B5 записали формулу =$D2+B$4. Затем ячейку B5 скопировали во все ячейки диапазона A5:F6. Какое наибольшее числовое значение появится в ячейках этого диапазона?
Примечание: знак $ обозначает абсолютную адресацию.
Заполним таблицу формулами:
Вычислим значения по полученным формулам:
Наибольшее числовое значение в ячейках диапазона A5:F6 равно 2900.
В ячейки электронной таблицы записаны числа, как показано ниже:
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 10 | 20 | 30 | 40 | 50 | 60 |
| 2 | 70 | 80 | 90 | 100 | 200 | 300 |
| 3 | 400 | 500 | 600 | 700 | 800 | 900 |
| 4 | 1200 | 1400 | 1600 | 1800 | 2000 | 2200 |
| 5 | ||||||
| 6 |
В ячейку С6 записали формулу =$B2+C$3. Затем ячейку C6 скопировали во все ячейки диапазона A5:F6. Какое наибольшее числовое значение появится в ячейках этого диапазона?
Примечание: знак $ обозначает абсолютную адресацию.
Заполним таблицу формулами:
Вычислим значения по полученным формулам:
Наибольшее числовое значение в ячейках диапазона A5:F6 равно 980.
Аналоги к заданию № 18488: 18619 Все
Квадрат разлинован на N×N клеток (1
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 41 и 22.
Источник: Демонстрационная версия ЕГЭ—2021 по информатике.Электронная таблица содержит результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время измерений максимальная суточная температура оказывалась выше среднесуточной на 7 и более градусов.
Электронная таблица содержит результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время измерений минимальная суточная температура оказывалась ниже среднесуточной на 8 и более градусов.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должна быть пара чисел 38 и 22.

Демоверсия КИМ ЕГЭ-2019 по информатике не претерпела никаких изменений по своей структуре по сравнению с 2018 годом. Это значимо упрощает работу педагога и, конечно, уже выстроенный (хочется на это рассчитывать) план подготовки к экзамену обучающегося.
Мы рассмотрим решение предлагаемого проекта (на момент написания статьи – пока еще проекта) КИМ ЕГЭ по информатике.
Часть 1
Задание 23
Сколько существует различных наборов значений логических переменных x1, x2, … x7, y1, y2, … y7, которые удовлетворяют всем перечисленным ниже условиям?
(y1 → (y2 /\ x1)) /\ (x1 → x2) = 1
(y2 → (y3 /\ x2)) /\ (x2 → x3) = 1
(y6 → (y7 /\ x6)) /\ (x6 → x7) = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, … x7, y1, y2, … y7, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Решение
Довольно детальный разбор данной категории задач был опубликован в свое время в статье «Системы логических уравнений: решение с помощью битовых цепочек» 3 .
И для дальнейших рассуждений мы вспомним (для наглядности выпишем) некоторые определения и свойства:
Посмотрим теперь на нашу систему еще раз. Обратим внимание, что ее можно переписать немного иначе. Для этого прежде всего заметим, что каждый из выделенных множителей в первых шести уравнениях, а также их взаимное произведение равны 1.
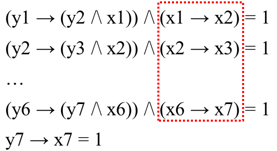
Немного поработаем над первыми множителями уравнений в системе:
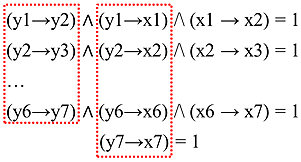
С учетом высказанных выше соображений, получим еще два уравнения, и исходная система уравнений примет вид:
В такой форме исходная система сводится к типовым заданиям, рассмотренным в указанной ранее статье.
Если рассмотреть отдельно первое и второе уравнения новой системы, то можно понять, что им соответствуют наборы:
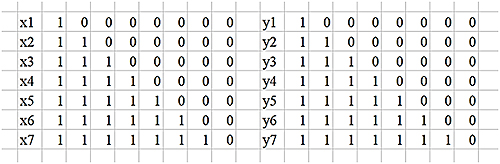
Эти рассуждения привели бы нас к возможным (8 × 8 = 64) вариантам решений, если бы не третье уравнение. В третьем уравнении мы сразу можем ограничиться рассмотрением только тех вариантов наборов, которые подходят для первых двух уравнений. Если подставить в третье уравнение первый набор y1…y7, состоящий только из 1, то очевидно, что ему будет соответствовать только один набор x1…x7, который также состоит только из 1. Любой другой набор, в котором есть хоть один 0, нам не подходит. Рассмотрим второй набор y1…y7 – 0111111. Для x1 допустимы оба возможных варианта значений – 0 и 1. Остальные значения, как и в предыдущем случае, не могут быть равны 0. Наборов, соответствующих данному условию, у нас два. Третьему набору y1…y7 – 011111 будут подходить первые три набора x1…x7. Рассуждая аналогично, мы получим, что искомое число наборов равно:
1 + 2 + … + 7 + 8 = 36.
Ответ: 36.
Заместитель генерального директора по ИКТ АНОО «Дом знаний», преподаватель по программированию Яндекс.Лицея (ДГУНХ, Махачкала), учитель высшей категории, финалист Всероссийского конкурса «Учитель года России 2010»
Читайте также:


