Реализуете в excel алгоритм вычисления площади круга с помощью метода монте карло
Существует много способов вычисления числа Пи. Самым простым и понятным является численный метод Монте-Карло, суть которого сводится к простейшему перебору точек на площади. Суть расчета заключается в том, что мы берем квадрат со стороной a = 2 R, вписываем в него круг радиусом R. И начинаем наугад ставить точки внутри квадрата. Геометрически, вероятность P1 того, чтот точка попадет в круг, равна отношению площадей круга и квадрата:
P1=Sкруг / Sквадрата = πR 2 / a 2 = πR 2 / (2 R ) 2 = πR 2 / (2 R) 2 = π / 4 (1)
Выглядит это так:
Вероятность попадания точки в круг можно также посчитать после численного эксперимента ещё проще: посчитать количество точек, попавших в круг, и поделить их на общее количество поставленных точек:
P2=Nпопавших в круг / Nточек; (2)
Так, при большом количестве точек в численном эксперименте вероятности должны вести себя cледующим образом:
lim(Nточек→∞)(P2-P1)=0; (3)
Следовательно:
π / 4 = Nпопавших в круг / Nточек; (4)
π =4 Nпопавших в круг / Nточек; (5)
НО! При моделировании мы применяем псевдослучайные числа, которые не являются случайным процессом.
Поэтому, выражение (5), к сожалению, строго не выполняется. Логичны вопросы, каковы оптимальные размеры квадрата и как много нужно применить точек?
Чтобы это выяснить, я написал такую программу:
Программа выводит значения числа Пи в зависимости от радиуса и количества точек. Единственное, что остается читателю, это скомпилировать её самостоятельно и запустить с параметрами, которые желает он.
Приведу лишь одну таблицу с полученными значениями:
| Радиус | Nточек | Pi |
| 102400 | 204800 | 3,145664 |
| 102400 | 409600 | 3,137188 |
| 102400 | 819200 | 3,139326 |
| 102400 | 1638400 | 3,144478 |
| 102400 | 3276800 | 3,139875 |
| 102400 | 6553600 | 3,142611 |
| 102400 | 13107200 | 3,140872 |
| 102400 | 26214400 | 3,141644 |
| 102400 | 52428800 | 3,141217 |
| 102400 | 1,05E+08 | 3,141324 |
| 102400 | 2,1E+08 | 3,141615 |
| 102400 | 4,19E+08 | 3,141665 |
| 102400 | 8,39E+08 | 3,141724 |
| 102400 | 1,68E+09 | 3,141682 |
Если что, значение числа Пи можно посмотреть с точностью до определенного знака здесь.
Источник картинки — википедия.
ЗАКАЗАТЬ РЕШЕНИЕ ЗАДАЧ МЕТОДОМ МОНТЕ-КАРЛО
Один из самых прикладных методов статистической оценки риска. К нему нужно отнестись с большим участием. В данной статье будет рассмотрен пример имитационного моделирования с использованием данного подхода.
Метод Монте-Карло получил своё название за то, что предназначен осуществить оценку предельно случайных событий. А что, как ни казино, которых в Монте-Карло много, связано со случайностью больше всего?
В процессе работы нам понадобится «генератор случайных чисел» из MS Excel и функция «Описательная статистика».
Оценка риска инвестиционного проекта
Есть следующие условия задачи:

Таким образом, нам нужно оценить три периода – за три года. Запишем все исходные данные в таблицу. Значения, полученные в ячейках D5-X5, имеют формулу для вычисления или есть в условиях задачи. Вы, как экономист, с формулами должны быть знакомы. Обратите внимание на заголовок, выделенный красным цветом на рисунке ниже – «Имитационная модель NCF1». Это говорит о том, что мы имитируем первый год, а всего их будет три на разных листах в MS Excel. На новый лист переключиться внизу окна программы.
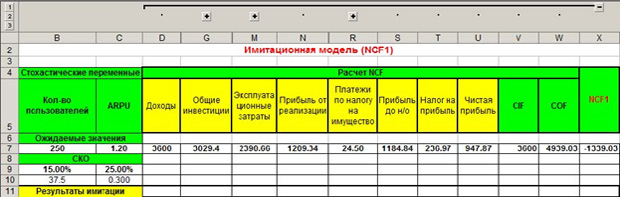
Теперь в MS Excel переключаемся на «Данные» и выбираем пункт «Анализ данных».

В появившемся окне выбираем «Генерация случайных чисел». Выполняем генерацию с параметрами, продемонстрированными на картинке ниже, для пункта «Кол-во пользователей».
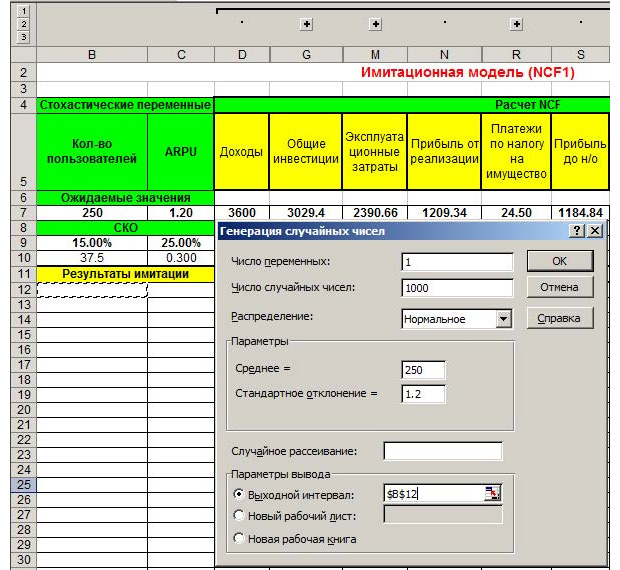
Параметры будут отталкиваться от среднего значения 250, оно есть в ожидаемых значениях в нашей таблице. Нужно выполнить 1000 генераций. Если вы знакомы со статистикой, то понимаете, что большее количество испытаний даёт более точную оценку. Используя метод Монте-Карло, можно имитировать и 10 000 значений для большей точности.
После мы имитируем все стохастические, то есть, меняющиеся значения по аналогии, как показано выше. Копируем формулы переменных или констант из ячеек D7-X7 под «Результаты имитации» с учетом имитированных значений. Получаем следующий результат.
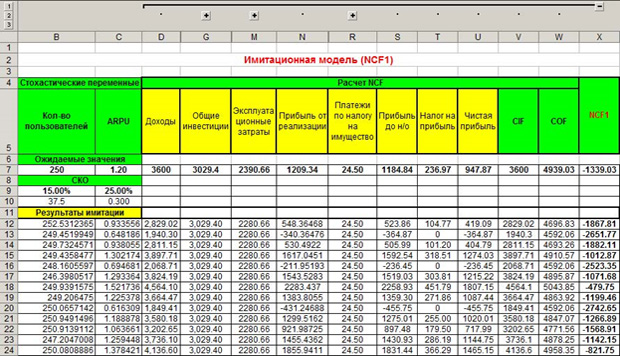
Как видим, платежи по налогам за имущество, например, являются постоянным значением на весь год, поэтому это значение везде одинаковое, а другие меняются, потому что рассчитываются по формулам, и в эти формулы входят меняющиеся значение, имитированные нами. Не забывайте, что значений в каждом столбце должно быть по тысяче.
Теперь делаем то же самое, но для имитационной модели NCF2.
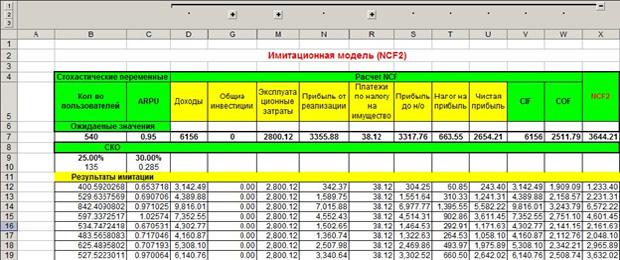
Это второй год работы проекта. Как видим, под «СКО» процентные соотношения увеличились. Об этом говорится в условии задачи, что налоги и зарплата должны расти каждый год.
Повторяем это действие в третий раз, увеличивая налоги и зарплаты, как говорит условие.
Наибольшую важность в оценке инвестиционного проекта имеет параметр NCF – чистый денежный поток. Копируем все значения NCF на четвертый лист с каждой из трёх предыдущих страниц.
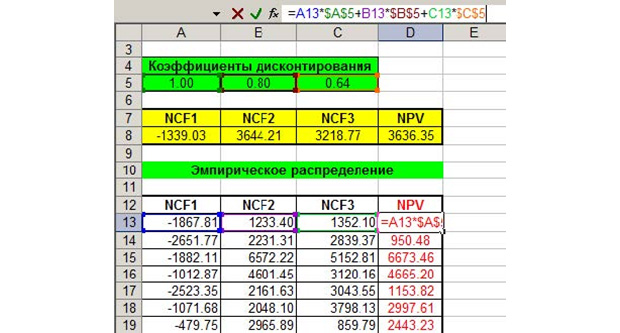
Формула для расчета NPV есть вверху картинки. Используем её. Теперь точно так же заходим в «Данные», жмём на «Анализ данных» и выбираем там «Описательная статистика». Вот, что в появившемся окне вам нужно указать.
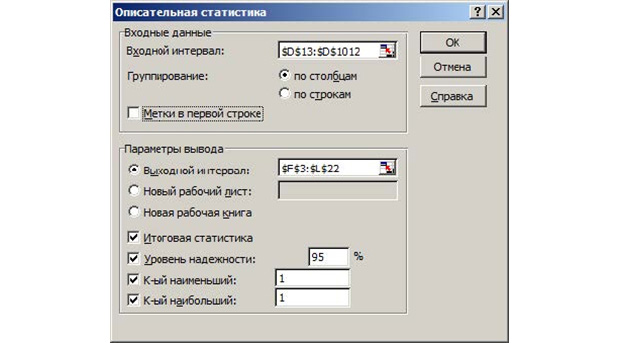
Во входном интервале выбирается 1000 полученных значений NPV. Выходной интервал можете выбрать произвольно. На выходе у вас будет таблица со статистическими данными.
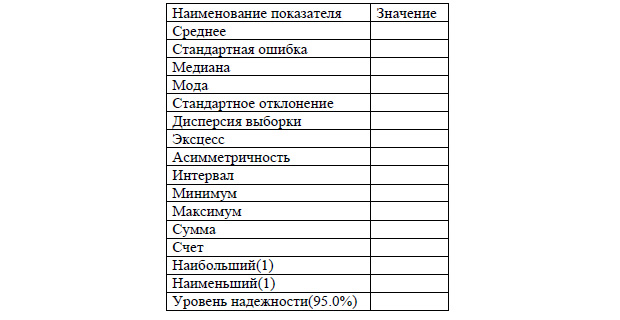
Вы, как экономист, должны понимать, о чем говорит каждое значение, если нет, то нужно прочитать отдельную статью или главу учебника. Наша статья о том, метод Монте-Карло применяется с использованием функций MS Excel.
Заключение
Генерация случайных чисел – наше всё. Именно в оценке того, к чему может привести случайность, заключается статистический метод Монте-Карло. Это работает не только в экономике, но и везде, где есть случайность. Можете посмотреть, как это делается, применительно к зоологии в видео ниже.
Для моделирования различных физических, экономических и других процессов широко распространены методы, называемые методами Монте-Карло. В их основе лежит метод статистических испытаний. Суть его состоит в том, что результат испытания ставится в зависимость от значения некоторой случайной величины, распределенной по заданному закону. Поэтому результат каждого отдельного испытания носит случайный характер.
Особенность метода состоит в том, что он гарантирует высокое качество статистических оценок только при весьма большом числе испытаний, которое невозможно выполнить без помощи компьютера.
Табличные процессоры не очень удобны для проведения расчетов Монте-Карло, однако с их использованием можно достаточно просто проиллюстрировать основные особенности этого метода.
Применение метода Монте-Карло для вычисления площади круга
Рассмотрим применение этого метода для вычисления площади круга заданного радиуса. Данная задача хорошо иллюстрирует возможности метода. Пусть круг имеет радиус R = 1 (рис. 1). Уравнение соответствующей окружности имеет вид: ( x – 1 )+ ( y – 1 )= 1. (1)

Для решения задачи методом Монте-Карло впишем круг в квадрат. Вершины квадрата будут иметь координаты (0,0), (2,0), (0,2), (2,2). Любая точка внутри квадрата или на его границе должна удовлетворять неравенствам 0 < x < 2 и 0 < y < 2. При случайном заполнении квадрата точками, координаты которых распределены равномерно в этих интервалах, часть точек будет попадать внутрь круга. Если выборка состоит из nнаблюдений и mточек попали внутрь круга или на окружность, то оценку площади круга Sможно получить из
S = S m /n (2)
где S – площадь квадрата, в который вписан круг.
В Excel с помощью функции СЛЧИС( ) можно получать равномерно распределенные случайные числа в диапазоне от 0 до 1. Для получения значений x и y в нужном диапазоне следует вводить формулы =2*СЛЧИС().
Число точек, попавших внутрь круга или на окружность, можно подсчитать, использовать функцию ЕСЛИ. Если координаты x и y таковы, что
Поэтому нужными формулами необходимо заполнить сразу большое число строк, например 500. Так будет выглядеть электронная таблица в режиме отображения формул:
| А | В | С | D |
| Х | У | =СУММ(С3:С502) | =C1/C2 |
| =СЧЁТ(С3:С502) | |||
| =2*СЛЧИС() | =2*СЛЧИС() | =ЕСЛИ(А3^2+B3^2<=1;1;0) | |
| … | … | … | … |
| =2*СЛЧИС() | =2*СЛЧИС() | =ЕСЛИ(А502^2+В502^2<=1;1;0) |
В ячейке D1 будет находиться результат – площадь фигуры.
Вычисляя отношение m/n при нарастающем числе испытаний, можно сделать выводы, справедливые для любого статистического эксперимента независимо от природы и типа моделируемой системы:
- с увеличением продолжительности наблюдения отклонение измеряемой
величины от ее точного значения уменьшается;
- существует предел, за которым увеличение продолжительности модели уже
не дает существенного повышения точности результата.
ЗАДАНИЕ
В соответствии с вариантом, методом Монте – Карло определить площадь фигур (см. рис. 1), и сравнить полученный результат с результатом, вычисленным по формуле.
| № варианта | |||||
| Фигура | Левая часть круга | Правая часть круга | Нижняя часть круга | Верхняя часть круга | Левая верхняя часть |
| № варианта | |||||
| Фигура | Левая верхняя часть круга | Правая верхняя часть круга | Правая нижняя часть круга | Левый верхний квадрант квадрата | Левый нижний квадрант квадрата |
| № варианта | |||||
| Фигура | Правый верхний квадрант квадрата | Правый нижний квадрант квадрата | Левый верхний треугольник | Правый верхний треугольник | Левый нижний треугольник |
| № варианта | |||||
| Фигура | Правый нижний треугольник | Верхняя половина квадрата | Нижняя половина квадрата | Левая половина квадрата | Правая половина квадрата |

Применительно к управлению Проектами, использование метода Монте – Карло позволяет нам оценить риск невыполнения проекта в срок или риск не уложиться в бюджет Проекта.
Рассмотрим сетевой график из лабораторной работы № и возьмем работы, формирующие критический путь.
Длина критического пути равна 10 дням. Однако, учитывая, что каждая работа имеет оптимистическую и пессимистическую оценки длительности, встает вопрос, а какова вероятность выполнения Проекта за 10 дней или, например, за 12 дней?
Моделирование методом Монте-Карло – это способ решения подобных задач. Необходимо случайным образом выбрать в указанных интервалах (от tо(i,j) до tп(i, j)) длительностей работ значения, и рассчитать длительность Проекта. Одни результаты превысят 10 дней (или 12 дней), а другие окажутся меньше. Процент реализаций, не превышающих 10 дней (12 дней), и будет искомой вероятностью.
Для моделирования надо знать форму кривой распределения. Для разных величин больше подходят кривые одной формы, чем другой. Мы будем использовать кривую нормального (гауссова) распределения. Это колоколообразная кривая, на которой большинство возможных значений результатов группируются в центральной части графика и лишь немногие, менее вероятные, распределяются, сходя на нет к его краям (рис. 1).
Вот как выглядит нормальное распределение:

Рис.1. Нормальное распределение
• значения, располагающиеся в центральной части графика, более вероятны, чем значения по его краям;
• распределение симметрично; медиана находится точно посредине между верхней и нижней границами 90%-ного доверительного интервала (CI);
• «хвосты» графика бесконечны; значения за пределами 90%-ного доверительного интервала маловероятны, но все же возможны.
Для построения нормального распределения в Excel можно воспользоваться функцией =НОРМРАСП(Х; Среднее; Стандартное_откл; Интегральная),
где Х – значение, для которого строится нормальное распределение;
Среднее – среднее арифметическое распределения; в нашем случае = 0;
Стандартное_откл – стандартное отклонение распределения; в нашем случае = 1;
Интегральная – логическое значение, определяющее форму функции; если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения; в нашем случае = ЛОЖЬ.
С нормальным распределением связано такое понятие, как стандартное отклонение. Рисунок 1 показывает, что в одном 90%-ном доверительном интервале насчитывается 3,29 стандартного отклонения.
В нашем примере создадим в электронной таблице генератор случайных чисел для каждого интервала значений (т.е. для каждой работы). Начнем с первой работы.
Воспользуемся формулой Excel: =НОРМОБР(вероятность;среднее;стандартное_откл),
где вероятность – вероятность, соответствующая нормальному распределению;
среднее – среднее арифметическое распределения;
стандартное_откл – стандартное отклонение распределения.
В нашем случае:
Среднее (медиана) = (Верхняя граница 90%-ного CI + Нижняя граница 90%-ного СI)/2 = (3+2)/2;
Стандартное отклонение = (Верхняя граница 90%-ного CI – Нижняя граница 90%-ного СI)/3,29 = (3-2)/3,29.
Таким образом, формула имеет вид:
где СЛЧИС – функция, генерирующая случайные числа в диапазоне от 0 до 1;
(3+2)/2 – среднее арифметическое диапазона MS;
(3-2)/3,29 – стандартное отклонение.
На рис. 2 представлен вариант исходных данных в Excel для данной задачи.

Рис. 2. Исходные данные для решения задачи
На рис. 3 представлена та же таблица в виде формул.

Рис.3. Таблица Excel с формулами
Предполагая, что количество экспериментов равно 100, заполним формулами 100 строчек – с 3 по 102.
Учитывая, что суммарная длина пути лежит в диапазоне от 7 до 14, а нам надо определить вероятность события, что мы выполним Проект за 10 (или 12) дней, разобьем весь диапазон на следующие отрезки: 7 и менее дней, от 7 до 10 дней, от 10 до 12 дней, от 12 до 14 дней, 14 и более дней. Формулы для подсчета попадания испытания в соответствующий интервал занесем в столбцы H,I,J,K,L.
Результаты представлены на рис. 4, а формулы для подсчета результатов и диаграмма, иллюстрирующая их, представлены на рис. 5.

Рис. 4. Результаты расчетов

Рис. 5. Формулы для подсчета результатов и диаграмма
Итак, по результатам работы можно сделать вывод, что Проект с вероятностью 36% мы закончим за 10 дней и с вероятностью 89% (36%+53%) за 12 дней.
ЗАДАНИЕ
Рассчитать вероятность завершения Проекта (в соответствии с выбранным вариантом) за время tкр и за время, большее, чем tкр на 10%. (округлить в большую сторону до целого числа дней). В качестве исходных данных, взять данные из лабораторной работы № .
В начале урока рассказываю идею метода. Ребята, сегодня мы рассмотрим интересный метод приближенного вычисления площадей фигур – метод Монте – Карло. Пусть у нас есть какая – нибудь фигура на плоскости, площадь которой ( Sfig ) нам необходимо найти. Ограничим ее другой фигурой, площадь которой ( Stotal ) мы можем легко вычислить. Например, прямоугольником АСDB со сторонами, параллельными координатным осям (см. рис. 1). И пусть про любую точку прямоугольника мы можем быстро узнать, попадает эта точка внутрь фигуры, площадь которой мы ищем, или нет.
А теперь начнем опыт – будем бросать на бумагу зерна случайным образом (вообще – то это нелегко сделать, чтобы обеспечить случайность). Когда нам покажется, что зерна почти полностью покрыли бумагу, посчитаем, сколько всего зерен на прямоугольнике (пусть их число Ntotal ) и сколько из них на фигуре ( Nfig ). Ясно, что число зерен, попавших внутрь фигуры, пропорционально ее площади: больше площадь – больше зерен, меньше площадь – меньше зерен. Поэтому, поделив количество зерен , попавших внутрь фигуры , на количество всех зерен в прямоугольнике, мы сможем найти, какую часть площади прямоугольника занимает фигура:
Промоделируем этот опыт на ЭВМ. Предположим, нам надо найти площадь фигуры ограниченной сверху кривой Y = F(X), а снизу – осью абсцисс. Пусть Y = cos(X), а Х I [– p /2, p /2] (см. рис. 2). Ограничим нашу фигуру прямоугольником АСDB, его площадь равна p .

Из чего должен состоять алгоритм:
1. Бросание зерна – бросание случайной точки, координаты X и Y которой случайны, причем Х должна меняться от – p /2 до p /2, а Y – от 0 до 1. И в этих интервалах X и Y должны появляться с одинаковой вероятностью в любой точке этих отрезков, т.е. X и Y должны быть равномерно распределены по осям. Тут надо напомнить ребятам, как получить равномерно распределенное случайное вещественное число на интервале [А, В]:
Х = random* ( B – A) + A
2. Надо определить, куда попала точка – под кривую или выше нее. И вести подсчет Nfig. Условие попадания точки под кривую: Y ? sin (X).
3. Повторить пп.1 и 2 столько раз, чтобы получить желаемую точность результатов.
Дети без труда напишут программу по данному алгоритму (на практическом занятии). И после этого наступает момент разочарования. Сухие цифры.
Предложение учителя: давайте создадим проект в Delphi, который наглядно демонстрировал бы работу метода Монте – Карло. Разработаем интерфейс программы. Тут ребята сами предлагают несколько вариантов оформления проекта, один из которых представлен на рис. 3.
Разместим на форме следующие компоненты:
Edit – окно редактирования для ввода общего количества испытаний (бросков зерен) – Ntotal;
Button – кнопка для запуска работы метода Монте – Карло;
Panel – панель для вывода посчитанной площади фигуры;
(все вышеперечисленные компоненты расположены на вкладке Standart Палитры компонентов)
Image – для вывода точек, попавших в искомую область (компонент расположен на вкладке Additional Палитры компонентов).
Если необходимо, надо напомнить ребятам некоторые свойства и методы выбранных компонентов (это может быть и домашним заданием предыдущего урока, чтобы не терять время на “воспоминания”) .
Компонент Edit:
Свойство Text – содержит текст, который пользователь набирает в окне Edit. Этот текст надо преобразовать в число Ntotal. Для этого в Delphi есть необходимая функция StrToInt:
Ntotal = StrToInt (Edit1.Text).
Компонент Panel:
Свойство Caption – содержит текст, который выводится на панель. Чтобы вывести полученное число Sfig на панель, мы должны преобразовать его в строку S с помощью процедуры Str:
а потом вывести эту строку на панель следующим образом:
Panel1.Caption := ‘Площадь фигуры = ‘ + S
Компонент Image:
Свойства Height и Width – соответственно высота и ширина компонента;
Свойство Canvas – отводит канву (место) для рисования на компоненте Image;
FillRect(ClientRect) – закрашивает область клиента компонента Image каким – либо цветом
(по – умолчанию – белым), т.е. стирает предыдущую картинку;
MoveTo(X, Y) – перемещает перо в точку с координатами X, Y без проведения линии (координаты задаются в пикселях);
LineTo(X, Y) – проводит линию из текущей точки в точку с координатами X, Y;
Pixels[I, J] – содержит цвет точки с координатами I, J.
У кнопки (компонент Button) мы будем обрабатывать событие onClick (событие нажатие кнопки). Т.е. вышеописанный алгоритм мы программируем в процедуре Button1Click.
Тут учитель задает вопрос классу: “ Какая проблема возникает при выводе точки на экран (на компонент Image)?” Ответ: расчетные координаты очень малы (0 ? Y ? 1,меньше пикселя, -p /2 ? X ? p /2); а если взять другую кривую Y = F(X), они могут оказаться слишком большими (больше размера компонента Image). Поэтому, при выводе значений функций (графиков) на экран монитора, необходимо преобразовывать расчетные координаты в графические с учетом дискретности растровой сетки монитора, а также предусмотреть возможность автоматического масштабирования функции (графика) по осям координат. Для этого желательно создать отдельную подпрограмму.
Для полного размещения функции (графика) в расчетной области (это область компонента Image) необходимо определить X_min, X_max, Y_min, Y_max – минимальные и максимальные значения по X и по Y соответственно. X_min =А, X_max = В. Как найти Y_min, Y_max.
Коллективно обсуждается следующий алгоритм:
1. Разобьем интервал [А, В] по Х на N равных частей и определим массивы значений аргумента и функции X[i] и Y[i] = F(X[i]), где I = 1..N;
2. Определяем наибольшее Y_max и наименьшее Y_min значения функции в заданном интервале изменения аргумента;
3. Находим коэффициенты масштабирования Kx, Ky при построении графика в заданной области;
4. Т.к. коэффициенты масштабирования Kx, Ky могут отличаться, то выводимый график может искажаться. Устраняем искажения графика;
5. Преобразуем расчетные координаты точки X, Y в графические Xg, Yg. С учетом того, необходимости “переворота” оси Y, которая в координатах монитора направлена сверху вниз.
Листинг программы, реализующей данные алгоритмы представлен в конце статьи. Результат работы программы при разном количестве испытаний представлен на рис. 3, 4.
Задания для самостоятельной работы:
1. Применить метод Монте – Карло для приближенного вычисления площади фигуры, ограниченной сверху кривой Y = sin (X), при Х I [ 0, p ];
2. Применить метод Монте – Карло для приближенного вычисления числа p . Подсказка: рассмотреть круг единичного радиуса с центром в т. (1, 1). Его площадь и будет равна p .
3. Применить метод Монте – Карло для приближенного вычисления площади фигуры, ограниченной сверху кривой Y = sin (X), при Х I [ 0, 2p ];
4. Применить метод Монте – Карло для приближенного вычисления площадей фигур, представленных на рис. 5 – 7.
5. Доработать проект:
а) организавать проверку правильности ввода информации в поле Edit (чтобы вводились только целые числа);
б) разметить оси и подписать числовые значения.
На последующих уроках, на которых предполагается изучение тем “Вычисление площадей (интегралов) методом трапеций и методом прямоугольников”, можно предложить ребятам доработать проект, поместив на форму дополнительные компоненты Image, Button, Edit, Panel (для каждого численного метода – свои). В окно компонента Edit пользователь будет вводить количество разбиений интервала [А, В] по Х. Таким образом, ребята смогут сравнить и наглядно увидеть работу всех трех численных методов.
unit Monte;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, ExtCtrls, Buttons;
type
TForm1 = class(TForm)
Panel1: TPanel;
BitBtn1: TBitBtn;
Edit1: TEdit;
Label1: TLabel;
Image1: TImage;
const A = -Pi/2.0; B = pi/2.0; n = 1000;
var
Form1: TForm1;
N_total:longint;
implementation
Function FUNC(x:real):real;
begin
Func:=Cos(x);
end;
Procedure Graphic( var right, down: integer;
var X_min, X_max, Y_min, Y_max, Kx, Ky: real);
type arr=array[1..n] of real;
var
X, Y: arr; dx: real;
i: integer;
begin
dx:=(B-A)/(n-1);
for i:=1 to n do begin X[i]:=A+dx*(i-1);
Y[i]:=FUNC(X[i]);
end;
X_max:=B; X_min:=A;
Y_max:=Y[1]; Y_min:=Y[1];
for i:=2 to n do begin
if Y_max < Y[i] then Y_max:=Y[i];
if Y_min > Y[i] then Y_min:=Y[i];
end;
Kx:=right/(X_max-X_min);
Ky:=down/(Y_max-Y_min);
if Kx < Ky then begin
Ky:=Kx;
down:=round((Y_max-Y_min)*Ky);
end
else begin
Kx:=Ky;
right:=round((X_max-X_min)*Kx);
end;
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
var N_total, N_fig, i:longint;
S_total,S_fig,X,Y:real;
Xg, Yg: integer;
X_min, X_max, Y_min, Y_max, Kx, Ky : real;
Right, Down: integer;
S:string;
begin
randomize;
With Image1, Canvas do
begin
FillRect(ClientRect);
Right := Width;
Down := Height;
Graphic(Right, Down, X_min, X_max, Y_min, Y_max, Kx, Ky);
Width := Right ;
Height := Down ;
MoveTo(Xg,Down);
LineTo(Xg, 0);
moveto(Xg, 0);
lineto(Xg+4, 10);
moveto(Xg, 0);
lineto(Xg-4, 10);
Ранее я рассмотрел пример использования метода Монте-Карло для расчета риска с применением стандартных средств Excel. К сожалению, Excel не очень подходит для решения такого рода задач, так как является детерминистской программой. В каждой отдельной ячейке может располагаться лишь конкретное значение, и для моделирования методом Монте-Карло требуется создать множество строк (сценариев), используя генератор случайных чисел (например, функцию СЛЧИС).
Существует немало программ для моделирования методом Монте-Карло. С их обзором можно ознакомиться, например, в книге Дугласа Хаббарда Как измерить всё, что угодно. Оценка стоимости нематериального в бизнесе:
| Инструмент | Кем разработан | Описание |
| @Risk | Palisade Corporation, Итака, штат Нью-Йорк | Достаточно совершенный инструмент для работы на основе Excel; описывает большое число распределений; широкая база пользователей, предоставляется техническая поддержка |
| AIE | Hubbard Decision Research, Глен-Эллин, штат Иллинойс | Набор макросов на основе Excel; также позволяет рассчитывать стоимость информации и оптимальный портфель; подчеркивает приоритетность методологии над инструментарием; предоставляются консалтинговые услуги по практическим вопросам внедрения |
| Crystal Ball | Decisioneering, Inc, Денвер, штат Колорадо | Еще один инструмент на базе Excel. Продукт, успешно конкурирующий с @Risk. Много пользователей, предоставляется техническая поддержка |
| Risk Solver Engine | Frontline Systems, Инклин-Вилладж, штат Невада | Уникальная платформа разработки на базе Excel, позволяющая выполнять моделирование методом Монте-Карло с беспрецедентной скоростью. Поддерживает форматы SIP и SLURPs, необходимые для управления вероятностями |
| SAS | SAS Corporation, Роли, штат Северная Каролина | Пакет программ высшей степени сложности, используемый многими профессиональными статистиками и далеко выходящий за рамки метода Монте-Карло |
| SPSS | SPSS Inc., Чикаго, штат Иллинойс | Также выходит за пределы метода Монте-Карло; весьма популярен среди ученых |
| XLSim | Профессор Стэнфордского университета Сэм Сэвидж, AnalyCorp | Недорогой пакет программ, предназначенный для легкого изучения, удобен в применении. Сэвидж проводит в организациях семинары по методу Монте-Карло |
Книга написана американским автором и вышла в США в 2007 г. Программа Crystal Ball, упомянутая в таблице сейчас принадлежит уже Oracle. Демо-версия программы доступна для скачивания с сайта компании. Описание базовых функциональных возможностей Crystal Ball я нашел на сайте Финансовое моделирование, бюджетирование, планирование.
Скачайте и установите Crystal Ball на ПК. Прежде чем запустить программу закройте все окна Excel. Запустите Crystal Ball. Сначала откроется Excel, а затем в нем появится закладка Crystal Ball (рис. 1).
Рис. 1. Запуск Crystal Ball сначала открывает Excel, а затем появляется закладка Crystal Ball
Воспользуемся примером Хаббарда, рассмотренным ранее, и на его основе изучим основы работы в программе Crystal Ball.
Предположим, что вы хотите арендовать новый станок. Стоимость годовой аренды станка 400 000 дол., и договор нужно подписать на несколько лет. Поэтому, даже не достигнув точки безубыточности, вы всё равно не сможете сразу вернуть станок. Вы собираетесь подписать договор, думая, что современное оборудование позволит сэкономить на трудозатратах и стоимости сырья и материалов, а также считаете, что материально-техническое обслуживание нового станка обойдется дешевле.
Ваши калиброванные специалисты [1] по оценке дали следующие интервалы значений ожидаемой экономии и годового объема производства (в таблице приведены 90%-ные доверительные интервалы):
| экономия на материально-техническом обслуживании | от 10 до 20 дол. на единицу продукции |
| экономия на трудозатратах | от «–2» до 8 дол. на единицу продукции |
| экономия на сырье и материалах | от 3 до 9 дол. на единицу продукции |
| объем производства | от 15 000 до 35 000 единиц продукции в год |
| годовая экономия | (MS + LS + RMS) х PL |
Шаг. 1. Формирование модели. Разместим исходные данные на листе Excel. Они будут включать названия параметров и их средние значения, а также формулу для расчета годовой экономии (рис. 2)
Рис. 2. Исходные данные
Таким образом, суть нашей модели – расчет годовой экономии от использования нового станка. Годовая экономия (зависимая переменная) есть функция трех видов экономии и объема производства (итого, четырех влияющих переменных).
Шаг. 2. Задание параметров распределения влияющих переменных. Встаньте в ячейку В2 и на вкладке Crystal Ball щелкните Define Assumption. В открывшемся окне выберите Normal и нажмите Ok
Рис. 3. Выбор нормального распределения для первого параметра «Экономия на материально-техническом обслуживании»
Задайте среднее значение – Mean и стандартное отклонение – Std. Dev. (рис. 4). Поскольку исходные данные сформулированы в терминах 90%-ного доверительного интервала (CI), формулы для расчета следующие:
Среднее (Mean) = (Верхняя граница 90%-ного CI + Нижняя граница 90%-ного СI)/2;
Стандартное отклонение (Std. Dev.) = (Верхняя граница 90%-ного CI – Нижняя граница 90%-ного СI)/3,29
а наша таблица, приспособленная для работы в Crystal Ball примет вид:
| Параметр | Границы 90%-ного доверительного интервала | Среднее | Стандартное отклонение |
| экономия на материально-техническом обслуживании | от 10 до 20 дол. на единицу продукции | 15 | 3,04 |
| экономия на трудозатратах | от «–2» до 8 дол. на единицу продукции | 3 | 3,04 |
| экономия на сырье и материалах | от 3 до 9 дол. на единицу продукции | 6 | 1,82 |
| объем производства | от 15 000 до 35 000 единиц продукции в год | 25 000 | 6 079 |
| годовая экономия | (MS + LS + RMS) х PL |
Рис. 4. Выбор параметров нормального распределения
Последовательно вставая курсором в ячейки В3:В5 выберите вид и параметры распределения для всех четырех влияющих переменных. После задания параметров ячейки окрашиваются в зеленый цвет.
Шаг 3. Выбор зависимой переменной. Встаньте в ячейку В6, содержащую формулу расчета годовой экономии, и щелкните Define Forecast. В открывшемся окне в поле «Units» укажите ссылку на ячейку (рис. 5).
Рис. 5. Выбор зависимой переменной
Шаг. 4. Выбор условий моделирования. Этот шаг не является обязательным, так как система предложит параметры моделирования по умолчанию. Учитывая, что наша модель довольно простая, можно увеличить число итераций (по умолчанию оно равно 1000). Щелкните Run Preferences, и выберите 10 000 (рис. 6). Чем больше итераций, тем надежней результаты моделирования!
Рис. 6. Выбор числа итераций
Шаг. 5. Запуск моделирования. Щелкните Start, и наслаждайте результатом вашего первого моделирования в Crystal Ball 🙂 После 10 000 итераций программа выведет результаты в графическом виде (рис. 7).
Рис. 7. Результаты моделирования – распределение годовой экономии
В будущем вы всегда можете увидеть результаты моделирования, если щелкните View Charts (рис. 8)
Рис. 8. Вывод диаграммы с результатами моделирования на экран монитора
Вы также можете создать отчет о моделировании (в отдельном файле Excel), если щелкните на Create Report (рис. 9).
Рис. 9. Фрагмент отчета.
Обратите внимание на величину стандартного отклонения прогнозного значения «Годовая экономия». Вспомним, что среднее значение и стандартное отклонение однозначно задают верхнюю и нижнюю границы 90%-ного доверительного интервала, и вычислим эти границы:
Нижняя граница = среднее – стандартное отклонение * 3,29 / 2 = 600 127 – 189 495 * 3,29 /2 = 288 408
Верхняя граница = среднее + стандартное отклонение * 3,29 / 2 = 600 127 + 189 495 * 3,29 /2 = 911 846
Видно, что не весь 90%-ный доверительный интервал «Годовой экономии» превышает точку безубыточности – 400 000 долл. То есть, существует вероятность того, что точка безубыточности достигнута не будет…
Заметим, что моделирование в Crystal Ball дало те же результаты, что и моделирование в Excel с помощью функции СЛЧИС (рис. 10).
Читайте также:




