Применение функций ms excel для решения математических и экономических задач

Обновлено: 07.01.2025

Аннотация научной статьи по экономике и бизнесу, автор научной работы — Конорева А. В., Гусева Г. С.

В статье показаны возможности предоставляемые программой Excel и ее встроенных инструментов, для решения производственных задач экономического характера. Сначала рассматриваются функции категорий «Математические» и «Статистические», позволяющие проводить простейший анализ экономических показателей. Далее поясняется, что для улучшения экономического анализа производства рекомендуется строить многофакторные математические модели и анализировать их с помощью математических и статистических функций.

Похожие темы научных работ по экономике и бизнесу , автор научной работы — Конорева А. В., Гусева Г. С.

Моделирование и вычислительный эксперимент в задаче прогнозирования среднедушевых денежных доходов населения на основе методов корреляционно-регрессионного анализа Адекватные междисциплинарные модели в прогнозировании временных рядов статистических данных Математическое моделирование влияния внешних факторов на параметры электропотребления Экономико-математическая модель и инструментарий прогнозирования и оптимизации расходов торгового предприятия по видам рекламы i Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

«EXCEL» mathimatically and statistically in economy

The article discusses business solution optimization using Microsoft Excel program associated tools. The article is organized in two sections. The first one discusses functions of categories «Mathematical» and «Statistical» those could be used for elementary analysis of statistical and economic data. The second part hints how to build multi-factor mathematical models of economic systems and how to analyze these models using mathematical and statistics functions.

Текст научной работы на тему «Использование математических и статистических функций Excel в экономике»

Вестник Омского университета. Серия «Экономика». 2009. № 3. С. 126-127. © А.В. Конорева, Г. С. Гусева, 2009

ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКИХ И СТАТИСТИЧЕСКИХ ФУНКЦИЙ EXCEL В ЭКОНОМИКЕ

«EXCEL» - MATHIMATICALLY AND STATISTICALLY IN ECONOMY

А.В. Конорева, Г.С. Гусева A.V. Konoreva, G.S. Gyseva

Омский государственный университет им. Ф.М. Достоевского

В статье показаны возможности предоставляемые программой Excel и ее встроенных инструментов, для решения производственных задач экономического характера. Сначала рассматриваются функции категорий «Математические» и «Статистические», позволяющие проводить простейший анализ экономических показателей. Далее поясняется, что для улучшения экономического анализа производства рекомендуется строить многофакторные математические модели и анализировать их с помощью математических и статистических функций.

The article discusses business solution optimization using Microsoft Excel program associated tools. The article is organized in two sections. The first one discusses functions of categories «Mathematical» and «Statistical» those could be used for elementary analysis of statistical and economic data. The second part hints how to build multi-factor mathematical models of economic systems and how to analyze these models using mathematical and statistics functions.

Ключевые слова: производственная функция, экономическая и статистическая функции.

Keywords: production function, economic and statistical functions.

В настоящее время для качественной организации деятельности предприятия широко применяют различное программное обеспечение. Существует множество специализированных программ для статистического анализа экономической информации. Но здесь особое внимание хочется уделить тем возможностям для обработки экономической информации, которые предоставляет Microsoft Excel, в частности, широкий набор инструментов для обработки данных, предоставляемый встроенными функциями. Помимо того, что различные функции облегчают вычисления и обработку текстовой информации используемой в отчетности, функции категорий «Математические» и «Статистические» значительно облегчают анализ экономических показателей.

Предположим, что сеть продуктовых магазинов хочет расширить круг клиентов, для чего необходимо обновить и увеличить ассортимент. Но сначала руководство хочет провести анализ доходов от реализации за последние месяцы.

Сначала подсчитаем сумму выручки трех магазинов за последние месяцы с помощью математической функции СУММ. Затем рассчитаем средний доход одного магазина по месяцам, используя функцию вычисления среднего значения, и округлим полученные значения тоже с помощью функции. С помощью статистических функций найдем максимальное и минимальное значения выручки от продаж за ме-

сяц. Если требуется не только вычислить наибольшее и наименьшее значения, но и расположить числа в порядке возрастания (убывания), то применяют функцию ранжирования.

Если мы предположим, что тенденция доходов от продаж, наблюдающаяся за последние три месяца, сохранится, то с помощью функции ТЕНДЕНЦИЯ мы сможем рассчитать величину доходов в следующих месяцах.

Конечно, результат, полученный таким образом, носит лишь оценочный характер, так как функция, рассчитывая линейную аппроксимацию по методу наименьших квадратов, опирается только на известный ряд данных, не принимая во внимание различные факторы, влияющие на оцениваемую ситуацию. Прогнозируя будущие доходы, необходимо учитывать изменения цен на горючее, политическую конъюнктуру, состояние других фирм. Поэтому, при всем том, что Excel позволяет нам вычислить математически точный результат, для полного анализа мы должны учитывать маркетинговые методики.

Существует самостоятельное направление экономических исследований - производственные функции. Производственную функцию можно определить как математическую модель исследуемого явления или процесса, которая в форме уравнения или их системы описывает зависимость результативного показателя от одного или ряда производственных факторов.

Рассмотрим производственную функцию в виде зависимости уровня оплаты труда (тыс. руб.) от производительности труда (тонн/час).

Производительность труда (тонн/час) Уровень оплаты труда (тыс. руб.)

Интенсивность связи между данными экономическими показателями определяется с помощью расчета коэффициента корреляции. Коэффициент корреляции можно рассчитать, используя статистическую функцию КОРРЕЛ.

В нашем случае при линейной зависимости коэффициент корреляции r = 0,867. Это соответствует высокой зависимости между данными признаками. Для того чтобы выбрать модель этой зависимости, надо рассмотреть ряд криволинейных зависимостей и выбрать ту, которая наилучшим образом аппроксимирует (выравнивает) эмпирические данные.

Для этого, используя возможности Microsoft Excel, легко построить различные (линейные, экспоненциальные, степенные, логарифмические) линии тренда по исходным данным, получив попутно их математическую запись и коэффициенты детерминации.

Анализируя коэффициенты детерминации, которые определяют долю влияния фактора, вошедшего в модель на результативный признак, выбираем наибольшее значение (R2 = 0,7845), и это означает, что в нашем случае степенная зависимость наилучшем образом аппроксимирует эмпирические данные.

В экономике и природе на результирующий показатель, как правило, влияют несколько факторов, поэтому изучение парных зависимостей обычно малоэффективно. В моделях, если эти модели претендуют на адекватность, необходимо учитывать совокупное влияние нескольких факторов. Это совокупное влияние факторов определяется методами множественной корреляции.

Например, в качестве производственной функции с использованием методов множественной корреляции можно рассмотреть зависимость между рентабельностью (результативный признак) и рядом факторов (механовооруженностью труда Х1, уровня сборности строительства Х2, коэффициента рассредоточенности строительства Х3, механизации строительномонтажных работ Х4, фондоотдачи Х5, текучести кадров Х6, определяемой как отношение уволенных работников к их среднесписочному числу).

По результативному показателю и всем факторам имеются репрезентативные выборки по производственной деятельности предприятия за ряд лет. По этим данным, с помощью пакета анализа, рассчитываются коэффициенты множественной корреляции и регрессии. В результате расчетов, получается уравнение регрессии, представляющее собой модель производственной деятельности предприятия.

Для оценки значимости этой модели, для определения значимости ее коэффициентов можно и нужно применять функции категорий «Математические» и «Статистические». А убедившись в значимости построенной модели и ее коэффициентов, а следовательно, и влияния соответствующих факторов на производство, можно давать рекомендации по изменению значимых факторов в сторону улучшения в соответствии с техническими, технологическими и организационными возможностями производства.

Опыт практического использования производственных функций показывает, что совершенствование на их основе анализа, прогнозирования, планирования и управления производством обеспечивает значительное повышение его экономической эффективности.

В заключение хочется заметить, что для решения экономических задач прикладного характера в настоящее время имеется много специализированных программ. Но приобретение такого программного обеспечения, его лицензирование и инсталляция могут сопровождаться определенными трудностями и проблемами, требовать дополнительных материальных вложений. В то же время программа Excel, которая приобретается, как приложение к широко распространенной операционной системе от Microsoft лишена этих трудностей. При этом использование математических и статистических функций Excel для решения экономических задач, для оптимизации производственного процесса не только ускоряет вычислительный процесс, но и делает его более простым, наглядным и доступным, уменьшает вероятность ошибок.

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

• Подбор параметров («Данные» - «Работа с данными» - «Анализ «что-если»» - «Подбор параметра») – находит значения, которые обеспечат нужный результат.
• Поиск решения (надстройка Microsoft Excel; «Данные» - «Анализ») – рассчитывает оптимальную величину, учитывая переменные и ограничения. Перейдите по ссылке и узнайте как подключить настройку «Поиск решения».
• Диспетчер сценариев («Данные» - «Работа с данными» - «Анализ «что-если»» - «Диспетчер сценариев») – анализирует несколько вариантов исходных значений, создает и оценивает наборы сценариев.

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» - 250 рублей. «3» - 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter - это обязательное условие для ввода массивов.

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Excel имеет значительную популярность среди бухгалтеров, экономистов и финансистов не в последнюю очередь благодаря обширному инструментарию по выполнению различных финансовых расчетов. Главным образом выполнение задач данной направленности возложено на группу финансовых функций. Многие из них могут пригодиться не только специалистам, но и работникам смежных отраслей, а также обычным пользователям в их бытовых нуждах. Рассмотрим подробнее данные возможности приложения, а также обратим особое внимание на самые популярные операторы данной группы.

Выполнение расчетов с помощью финансовых функций

В группу данных операторов входит более 50 формул. Мы отдельно остановимся на десяти самых востребованных из них. Но прежде давайте рассмотрим, как открыть перечень финансового инструментария для перехода к выполнению решения конкретной задачи.

Переход к данному набору инструментов легче всего совершить через Мастер функций.

1. Выделяем ячейку, куда будут выводиться результаты расчета, и кликаем по кнопке «Вставить функцию», находящуюся около строки формул.

В Мастер функций также можно перейти через вкладку «Формулы». Сделав переход в неё, нужно нажать на кнопку на ленте «Вставить функцию», размещенную в блоке инструментов «Библиотека функций». Сразу вслед за этим запустится Мастер функций.

Имеется в наличии также способ перехода к нужному финансовому оператору без запуска начального окна Мастера. Для этих целей в той же вкладке «Формулы» в группе настроек «Библиотека функций» на ленте кликаем по кнопке «Финансовые». После этого откроется выпадающий список всех доступных инструментов данного блока. Выбираем нужный элемент и кликаем по нему. Сразу после этого откроется окно его аргументов.

ДОХОД

Одним из наиболее востребованных операторов у финансистов является функция ДОХОД. Она позволяет рассчитать доходность ценных бумаг по дате соглашения, дате вступления в силу (погашения), цене за 100 рублей выкупной стоимости, годовой процентной ставке, сумме погашения за 100 рублей выкупной стоимости и количеству выплат (частота). Именно эти параметры являются аргументами данной формулы. Кроме того, имеется необязательный аргумент «Базис». Все эти данные могут быть введены с клавиатуры прямо в соответствующие поля окна или храниться в ячейках листах Excel. В последнем случае вместо чисел и дат нужно вводить ссылки на эти ячейки. Также функцию можно ввести в строку формул или область на листе вручную без вызова окна аргументов. При этом нужно придерживаться следующего синтаксиса:

Главной задачей функции БС является определение будущей стоимости инвестиций. Её аргументами является процентная ставка за период («Ставка»), общее количество периодов («Кол_пер») и постоянная выплата за каждый период («Плт»). К необязательным аргументам относится приведенная стоимость («Пс») и установка срока выплаты в начале или в конце периода («Тип»). Оператор имеет следующий синтаксис:

Оператор ВСД вычисляет внутреннюю ставку доходности для потоков денежных средств. Единственный обязательный аргумент этой функции – это величины денежных потоков, которые на листе Excel можно представить диапазоном данных в ячейках («Значения»). Причем в первой ячейке диапазона должна быть указана сумма вложения со знаком «-», а в остальных суммы поступлений. Кроме того, есть необязательный аргумент «Предположение». В нем указывается предполагаемая сумма доходности. Если его не указывать, то по умолчанию данная величина принимается за 10%. Синтаксис формулы следующий:

Оператор МВСД выполняет расчет модифицированной внутренней ставки доходности, учитывая процент от реинвестирования средств. В данной функции кроме диапазона денежных потоков («Значения») аргументами выступают ставка финансирования и ставка реинвестирования. Соответственно, синтаксис имеет такой вид:

ПРПЛТ

Оператор ПРПЛТ рассчитывает сумму процентных платежей за указанный период. Аргументами функции выступает процентная ставка за период («Ставка»); номер периода («Период»), величина которого не может превышать общее число периодов; количество периодов («Кол_пер»); приведенная стоимость («Пс»). Кроме того, есть необязательный аргумент – будущая стоимость («Бс»). Данную формулу можно применять только в том случае, если платежи в каждом периоде осуществляются равными частями. Синтаксис её имеет следующую форму:

Оператор ПЛТ рассчитывает сумму периодического платежа с постоянным процентом. В отличие от предыдущей функции, у этой нет аргумента «Период». Зато добавлен необязательный аргумент «Тип», в котором указывается в начале или в конце периода должна производиться выплата. Остальные параметры полностью совпадают с предыдущей формулой. Синтаксис выглядит следующим образом:

Формула ПС применяется для расчета приведенной стоимости инвестиции. Данная функция обратная оператору ПЛТ. У неё точно такие же аргументы, но только вместо аргумента приведенной стоимости («ПС»), которая собственно и рассчитывается, указывается сумма периодического платежа («Плт»). Синтаксис соответственно такой:

Следующий оператор применяется для вычисления чистой приведенной или дисконтированной стоимости. У данной функции два аргумента: ставка дисконтирования и значение выплат или поступлений. Правда, второй из них может иметь до 254 вариантов, представляющих денежные потоки. Синтаксис этой формулы такой:

СТАВКА

Функция СТАВКА рассчитывает ставку процентов по аннуитету. Аргументами этого оператора является количество периодов («Кол_пер»), величина регулярной выплаты («Плт») и сумма платежа («Пс»). Кроме того, есть дополнительные необязательные аргументы: будущая стоимость («Бс») и указание в начале или в конце периода будет производиться платеж («Тип»). Синтаксис принимает такой вид:

ЭФФЕКТ

Оператор ЭФФЕКТ ведет расчет фактической (или эффективной) процентной ставки. У этой функции всего два аргумента: количество периодов в году, для которых применяется начисление процентов, а также номинальная ставка. Синтаксис её выглядит так:

Нами были рассмотрены только самые востребованные финансовые функции. В общем, количество операторов из данной группы в несколько раз больше. Но и на данных примерах хорошо видна эффективность и простота применения этих инструментов, значительно облегчающих расчеты для пользователей.

Мы рады, что смогли помочь Вам в решении проблемы.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

В Microsoft Excel предусмотрено огромное количество разнообразных функций, позволяющих справляться с математическими, экономическими, финансовыми и другими задачами. Программа является одним из основных инструментов, использующихся в малых, средних и больших организациях для ведения различных видов учета, выполнения расчетов и т.д. Ниже мы рассмотрим финансовые функции, которые наиболее востребованы в Экселе.

Вставка функции

Для начала вспомним, как вставить функцию в ячейку таблицы. Сделать это можно по-разному:

Независимо от выбранного варианта, откроется окно вставки функции, в котором требуется выбрать категорию “Финансовые”, определиться с нужным оператором (например, ДОХОД), после чего нажать кнопку OK.

На экране отобразится окно с аргументами функции, которые требуется заполнить, после чего нажать кнопку OK, чтобы добавить ее в выбранную ячейку и получить результат.

Указывать данные можно вручную, используя клавиши клавиатуры (конкретные значения или ссылки на ячейки), либо встав в поле напротив нужного аргумента, выбирать соответствующие элементы в самой таблице (ячейки, диапазон ячеек) с помощью левой кнопки мыши (если это допустимо).

Обратите внимание, что некоторые аргументы могут не показываться и необходимо пролистать область вниз для получения доступа к ним (с помощью вертикального ползункам справа).

Альтернативный способ

Находясь во вкладке “Формулы” можно нажать кнопку “Финансовые” в группе “Библиотека функций”. Раскроется список доступных вариантов, среди которых просто кликаем по нужному.

После этого сразу же откроется окно с аргументами функции для заполнения.

Популярные финансовые функции

Теперь, когда мы разобрались с тем, каким образом функция вставляется в ячейку таблицы Excel, давайте перейдем к перечню финансовых операторов (представлены в алфавитном порядке).

Данный оператор применяется для вычисления будущей стоимости инвестиции исходя из периодических равных платежей (постоянных) и размера процентной ставки (постоянной).

Обязательными аргументами (параметрами) для заполнения являются:

• Ставка – процентная ставка за период;
• Кпер – общее количество периодов выплат;
• Плт – неизменная выплата за каждый период.

Необязательные аргументы:

• Пс – приведенная (нынешняя) стоимость. Если не заполнять, будет принято значение, равное “0”;
• Тип – здесь указывается:
  • 0 – выплата в конце периода;
  • 1 – выплата в начале периода
  • если поле оставить пустым, по умолчанию будет принято нулевое значение.

  Также есть возможность вручную ввести формулу функции сразу в выбранной ячейке, минуя окна вставки функции и аргументов.

  Синтаксис функции:

  Результат в ячейке и выражение в строке формул:

  
  

  Функция позволяет вычислить внутреннюю ставку доходности для ряда денежных потоков, выраженных числами.

  
  

  Обязательный аргумент всего один – “Значения”, в котором нужно указать массив или координаты диапазона ячеек с числовыми значениями (по крайней мере, одно отрицательное и одно положительное число), по которым будет выполняться расчет.

  Необязательный аргумент – “Предположение”. Здесь указывается предполагаемая величина, которая близка к результату ВСД. Если не заполнять данное поле, по умолчанию будет принято значение, равное 10% (или 0,1).

  Синтаксис функции:

  Результат в ячейке и выражение в строке формул:

  
  

  ДОХОД

  С помощью данного оператора можно посчитать доходность ценных бумаг, по которым производится выплата периодического процента.

  
  

  Обязательные аргументы:

  • Дата_согл – дата соглашения/расчета по ценным бумагам (далее – ц.б.);
  • Дата_вступл_в_силу – дата вступления в силу/погашения ц.б.;
  • Ставка – годовая купонная ставка ц.б.;
  • Цена – цена ц.б. за 100 рублей номинальной стоимости;
  • Погашение – суммы погашения или выкупная стоимость ц.б. за 100 руб. номинальной стоимости;
  • Частота – количество выплат за год.

  Аргумент “Базис” является необязательным, в нем задается способ вычисления дня:

  • 0 или не заполнен – армериканский (NASD) 30/360;
  • 1 – фактический/фактический;
  • 2 – фактический/360;
  • 3 – фактический/365;
  • 4 – европейский 30/360.

  Синтаксис функции:

  Результат в ячейке и выражение в строке формул:

  
  

  Оператор используется для расчета внутренней ставки доходности для ряда периодических потоков денежных средств исходя из затрат на привлечение инвестиций, а также процента от реинвестирования денег.

  
  

  У функции только обязательные аргументы, к которым относятся:

  • Значения – указываются отрицательные (платежи) и положительные числа (поступления), представленные в виде массива или ссылок на ячейки. Соответственно, здесь должно быть указано, как минимум, одно положительное и одно отрицательное числовое значение;
  • Ставка_финанс – выплачиваемая процентная ставка за оборачиваемые средства;
  • Ставка _реинвест – процентная ставка при реинвестировании за оборачиваемые средства.

  Синтаксис функции:

  Результат в ячейке и выражение в строке формул:

  
  

  ИНОРМА

  Оператор позволяет вычислить процентную ставку для полностью инвестированных ц.б.

  
  

  Аргументы функции:

  • Дата_согл – дата расчета по ц.б.;
  • Дата_вступл_в_силу – дата погашения ц.б.;
  • Инвестиция – сумма, вложенная в ц.б.;
  • Погашение – сумма к получению при погашении ц.б.;
  • аргумент “Базис” как и для функции ДОХОД является необязательным.

  Синтаксис функции:

  Результат в ячейке и выражение в строке формул:

  
  

  С помощью этой функции рассчитывается сумма периодического платежа по займу исходя из постоянства платежей и процентной ставки.

  
  

  Обязательные аргументы:

  • Ставка – процентная ставка за период займа;
  • Кпер – общее количество периодов выплат;
  • Пс – приведенная (нынешняя) стоимость.

  Необязательные аргументы:

  • Бс – будущая стоимость (баланс после последней выплаты). Если поле оставить незаполненным, по умолчанию будет принято значение, равное “0”.
  • Тип – здесь указывается, как будет производиться выплата:
    • “0” или не указано – в конце периода;
    • “1” – в начале периода.

    Синтаксис функции:

    Результат в ячейке и выражение в строке формул:

    
    

    ПОЛУЧЕНО

    Применяется для нахождения суммы, которая будет получена к сроку погашения инвестированных ц.б.

    
    

    Аргументы функции:

    • Дата_согл – дата расчета по ц.б.;
    • Дата_вступл_в_силу – дата погашения ц.б.;
    • Инвестиция – сумма, инвестированная в ц.б.;
    • Дисконт – ставка дисконтирования ц.б.;
    • “Базис” – необязательный аргумент (см. функцию ДОХОД).

    Синтаксис функции:

    Результат в ячейке и выражение в строке формул:

    
    

    Оператор используется для нахождения приведенной (т.е. к настоящему моменту) стоимости инвестиции, которая соответствует ряду будущих выплат.

    
    

    Обязательные аргументы:

    • Ставка – процентная ставка за период;
    • Кпер – общее количество периодов выплат;
    • Плт – неизменная выплата за каждый период.

    Необязательные аргументы – такие же как и для функции “ПЛТ”:

    Синтаксис функции:

    Результат в ячейке и выражение в строке формул:

    
    

    СТАВКА

    Оператор поможет найти процентную ставку по аннуитету (финансовой ренте) за 1 период.

    
    

    Обязательные аргументы:

    • Кпер – общее количество периодов выплат;
    • Плт – неизменная выплата за каждый период;
    • Пс – приведенная стоимость.

    Необязательные аргументы:

    • Бс – будущая стоимость (см. функцию ПЛТ);
    • Тип (см. функцию ПЛТ);
    • Предположение – предполагаемая величина ставки. Если не указывать, будет принято значение по умолчанию – 10% (или 0,1).

    Синтаксис функции:

    Результат в ячейке и выражение в строке формул:

    
    

    Оператор позволяет найти цену за 100 рублей номинальной стоимости ц.б., по которым производится выплата периодического процента.

    
    

    Обязательные аргументы:

    • Дата_согл – дата расчета по ц.б.;
    • Дата_вступл_в_силу – дата погашения ц.б.;
    • Ставка – годовая купонная ставка ц.б.;
    • Доход – годовой доход по ц.б.;
    • Погашение – выкупная стоимость ц.б. за 100 руб. номинальной стоимости;
    • Частота – количество выплат за год.

    Аргумент “Базис” как и для оператора ДОХОД является необязательным.

    Синтаксис функции:

    Результат в ячейке и выражение в строке формул:

    
    

    С помощью данной функции можно определить чистую приведенную стоимость инвестиции исходя из ставки дисконтирования, а также размера будущих поступлений и платежей.

    
    

    Аргументы функции:

    • Ставка – ставка дисконтирования за 1 период;
    • Значение1 – здесь указываются выплаты (отрицательные значения) и поступления (положительные значения) в конце каждого периода. Поле может содержать до 254 значений.
    • Если лимит аргумента “Значение 1” исчерпан, можно перейти к заполнению следующих – “Значение2”, “Значение3” и т.д.

    Синтаксис функции:

    Результат в ячейке и выражение в строке формул:

    
    

    Заключение

    Категория “Финансовые” в программе Excel насчитывает свыше 50 различных функций, но многие из них специфичны и узконаправлены, из-за чего используются редко. Мы же рассмотрели 11 самых востребованных, по нашему мнению.

    
    

    Научитесь использовать все прикладные инструменты из функционала MS Excel.

    Microsoft Excel – одна из самых популярных и легкодоступных программ для представителей разный специальностей. Сегодня мы рассмотрим, пожалуй, одну из самых используемых групп формул – математические формулы.

    Начнем с того, как найти их среди прочего функционала. Есть несколько путей того, как открыть список математических формул.

    Самый простой способ – нажать на кнопку «Формулы» на панели управления. Затем выбрать из перечня тип функций: «Математические».

    Перед вами появится выпадающий длинный список всех существующих операторов:

    Всего в Excel около 80 математических и тригонометрических функций. Мы рассмотрим не все, только самые распространенные из них, а также обратим внимание на некоторые нюансы, о которых вы, возможно, не знали. Если в статье вы не нашли нужную вам функцию, то скачивайте наш бесплатный гайд «Математические функции в Excel».

    Для разминки вспомним самые простые формулы.

    1. Формулы СУММ(), ПРОИЗВЕД()

    Эти операции имеют схожую структуру и одинаковый тип аргументов, поэтому мы их объединили в один блок. СУММ() служит для сложения данных в нескольких ячейках, ПРОИЗВЕД() – очевидно, для нахождения произведения.

    Аргументами этих функций могут быть числа, диапазоны, ссылки на ячейку, в которой содержится числовое значение. Количество элементов не может быть больше 30.

    СУММ() и ПРОИЗВЕД() пропускают пустые ячейки, ячейки текстового формата и логические значения. Операторы вносят результат вычислений в отдельную, ранее выделенную курсором ячейку:

    Аналогично для формулы ПРОИЗВЕД():

    2. Формула ЧАСТНОЕ()

    Тоже одна из простых операций в математике. В Excel выполняется тоже несложно: у функции ЧАСТНОЕ() есть два аргумента: делимое и делитель.

    В выделенной ячейке выводится частное:

    
    

    3. Формула СУММЕСЛИ()

    В качестве условий могут выступать неравенства со знаками больше, меньше или не равно («>», «<», «< >»). Число, которое не соответствует введенному условию, не будет включен в суммирование.

    На рисунке 5 изображено суммирование всех чисел, которые больше 0.

    Оранжевым выделены те числа, которые будут включены в расчет функцией СУММЕСЛИ().

    Остальные числа просто будут игнорироваться:

    Кроме постоянных аргументов, существует еще и дополнительный – «Диапазон суммирования». Он добавляется тогда, когда необходимо просуммировать один диапазон, а условия выбирать по другому диапазону.

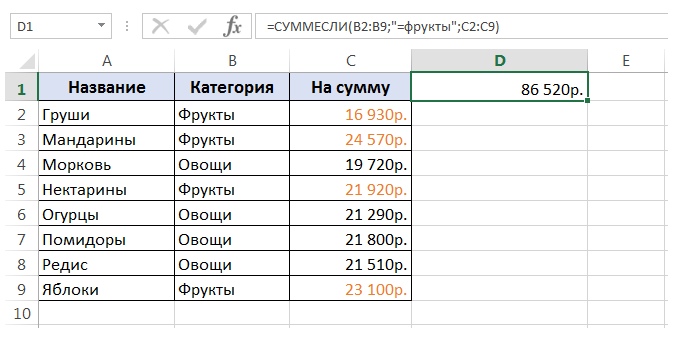
    Например, нужно посчитать общую стоимость всех проданных фруктов.

    Для этого воспользуемся следующей формулой:

    
    

    Рис. 6 Пример с функцией СУММЕСЛИ() с необязательным аргументом «Диапазон суммирования

    То есть сначала пишем диапазон, по которому проверяем условие, затем само ограничение и в конце диапазон чисел, которые надо суммировать. В примере на рисунке 6 выше, соответственно, все строки из категории «Овощи» в расчет включены не будут.

    4. Формулы ОКРУГЛ(), ОКРУГЛВВЕРХ(), ОКРУГЛВНИЗ()

    Функция ОКРУГЛ() предназначена для округления значения до заданного количества знаков после запятой. В качестве первого аргумента выступают, как обычно, числа или диапазон ячеек, второго – разряд, до которого нужно округлить число.

    Например, округление значения до второго знака после запятой:

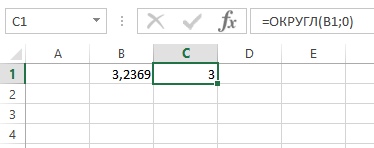
    Если в качестве второго аргумента выступает 0, то число будет округляться до ближайшего целого:

    
    

    Рис. 8 Применение функции ОКРУГЛ() до целого значения

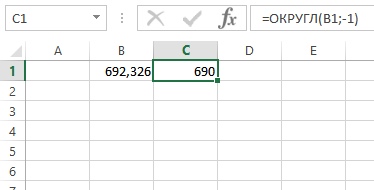
    Второй аргумент может быть и отрицательным, тогда округление будет происходить до требуемого знака перед запятой:

    
    

    9. Рис. Применение функции ОКРУГЛ(), когда второй аргумент меньше 0

    Если необходимо округлить в сторону меньшего или большего по модулю числа используют функции ОКРУГЛВНИЗ(), ОКРУГЛВВЕРХ(), соответственно:

    Замечание: многие могут решить, что функции округления бесполезны, так как можно просто убрать/добавить дополнительный знак после запятой с помощью кнопок увеличить/уменьшить разрядность.

    На самом деле, это не так.

    Дело в том, что увеличение или уменьшение разрядности влияет только на «внешний вид» ячейки, то есть на то, как мы число видим.

    Само число, при этом, не меняется. Функции округления же полностью меняют вид числа, убирая лишние разряды.

    5. Формулы ОТБР(), ЦЕЛОЕ()

    Эти функции очень похожи на предыдущие, но работают немного по-другому.

    ОТБР() убирает все цифры справа от запятой и у положительных, и у отрицательных чисел. На первом месте в скобках после оператора пишется значение, а на втором – разряд, после которого удалятся все знаки.

    Если второй аргумент пропущен, то по умолчанию ставится 0:

    ЦЕЛОЕ() – функция, которая выдает в качестве результата наименьшее целое число, стоящее перед аргументом:

    На положительные числа операторы влияют почти одинаково, а вот на отрицательные – нет.

    Функция ЦЕЛОЕ(-5,6) выдаст результат (-6), а ОТБР(-5,6;0) выдаст (-5), хотя в то же время для числа 5,3 результат обеих функций будет одинаковый – число (5).

    6. Формула ABS()

    Математическая формула ABS() позволяет получить число по модулю. Как обычно, аргументами оператора является число или ссылка на ячейку.

    Эту функцию удобно использовать, например, когда необходимо найти количество дней между датами. Из школьной программы многие знают, что нужно из большего вычитать меньшее.

    Но что делать если дана огромная таблица, где трудно определить, где какое значение? Здесь нам помогает оператор ABS(), который переводит отрицательное число в положительное.

    7. Формула КОРЕНЬ()

    Замечание. Для извлечения корня другой степени (не квадратного) можно пользоваться функцией СТЕПЕНЬ().

    8. Формула СТЕПЕНЬ()

    Функция СТЕПЕНЬ() позволяет возвести число в любую степень, в том числе извлечь корень (то есть возвести число в дробную степень).

    Например, чтобы извлечь кубический корень из числа 8, необходимо воспользоваться формулой, как на рисунке 17.1.

    
    

    Рис.17.1 Применение функции СТЕПЕНЬ() для извлечения кубического корня

    Если вам интересно узнать больше о других математических функциях, напишите об этом ниже в комментариях. Записывайтесь на открытый онлайн-курс «Аналитика в Excel», если хотите научиться выполнять рутинную работу в программе быстрее.

    
    

    Научитесь использовать все прикладные инструменты из функционала MS Excel.

    Читайте также:

      
    • Список стандартных реквизитов позволяет 1с
      
    • Метод объекта не обнаружен 1с
      
    • Программа для распаковки zip файлов для виндовс 10
      
    • Что такое инкассовое поручение в 1с
      
    • Как добавить товар в 1с управление торговлей