Построить верхнюю ветвь эвольвенты окружности в эксель

Урок посвящен построению зубчатого колеса с эвольвентным профилем зуба. Урок состоит из двух частей. В первой части выложена теория, формулы для расчета и один из способов графического построения эвольвентного профиля зуба.
Во второй части (видео) показан способ построения модели зубчатого колеса с использованием графических построений в первой части урока.
Часто задаваемые вопросы:
*Что такое эвольвента (эволюта)?
*Как построить эвольвенту?
*Как построить зубчатое колесо в программе SolidWorks?
*Формулы для расчета зубчатого колеса?
*Как нарисовать эвольвентный профиль зуба зубчатого колеса?
Итак, начнем с теории.
Эвольвентное зацепление позволяет передавать движение с постоянным передаточным отношением. Эвольвентное зацепление - зубчатое зацепление, в котором профили зубьев очерчены по эвольвенте окружности.
Для этого необходимо чтобы зубья зубчатых колёс были очерчены по кривой, у которой общая нормаль, проведённая через точку касания профилей зубьев, всегда проходит через одну и туже точку на линии, соединяющей центры зубчатых колёс, называемую полюсом зацепления.
Параметры зубчатых колёс
Основной теореме зацепления удовлетворяют различные кривые, в том числе эвольвента и окружность, по которым чаще всего изготавливают профили зубьев зубчатого колеса.
В случае, если профиль зуба выполнен по эвольвенте, передача называется эвольвентной.
Для передачи больших усилий с помощью зубчатых механизмов используют зацепление Новикова, в котором профиль зуба выполнен по окружности.
Окружности, которые катятся в зацеплении без скольжения друг по другу, называются начальными (D).
Окружности, огибающие головки зубьев зубчатых колёс, называются окружностями головок (d1).
Окружности, огибающие ножки зубьев зубчатых колёс, называются окружностями ножек (d2).
Окружности, по которым катятся прямые, образующие эвольвенты зубьев первого и второго колёс, называются основными окружностями.
Окружность, которая делит зуб на головку и ножку, называется делительной окружностью (D).
Для нулевых (некорригированных) колёс начальная и делительная окружности совпадают.
Расстояние между одноимёнными точками двух соседних профилей зубьев зубчатого колеса называется шагом по соответствующей окружности.
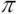
Шаг можно определить по любой из пяти окружностей. Чаще всего используют делительный шаг p =2r/z, где z – число зубьев зубчатого колеса. Чтобы уйти от иррациональности в расчётах параметров зубчатых колёс, в рассмотрение вводят модуль, измеряемый в миллиметрах, равный
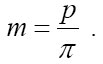
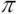
Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности (D) к числу зубьев z или отношению шага p к числу "пи" .
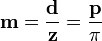
Модуль зубчатого колеса стандартизованы, что является основой для стандартизации других параметров зубчатых колёс.
Основные формулы для расчета эвольвентного зацепления:
Исходными данными для расчета как эвольвенты, так и зубчатого колеса являются следующие параметры: m - Модуль - часть диаметра делительной окружности приходящаяся на один зуб. Модуль - стандартная величина и определяется по справочникам. z - количество зубьев колеса. ? ("альфа") - угол профиля исходного контура. Угол является величиной стандартной и равной 20°.
Делительный диаметр рассчитывается по формуле:
Диаметр вершин зубьев рассчитывается по формуле:
d1=D+2m
Диаметр впадин зубьев рассчитывается по формуле:
d2=D-2*(c+m)
где с - радиальный зазор пары исходных контуров. Он определяется по формуле:
с = 0,25m
Диаметр основной окружности, развертка которой и будет составлять эвольвенту, определяется по формуле:
d3 = cos ? * D
От автора. Я нашел в интернете полезную программку в Excel 2007. Это автоматизированная табличка для расчета всех параметров прямозубого зубчатого колеса.
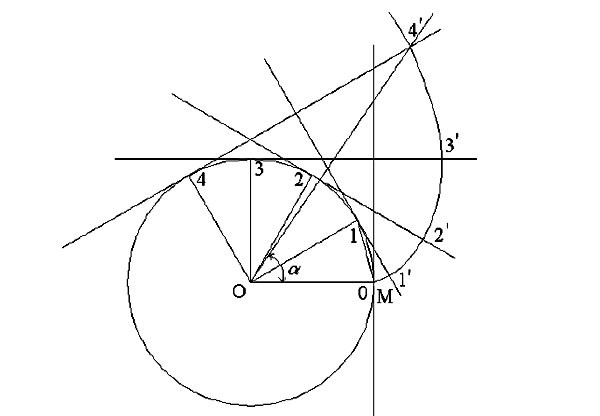
Итак, приступим к графическому построению профиля зубчатого колеса.
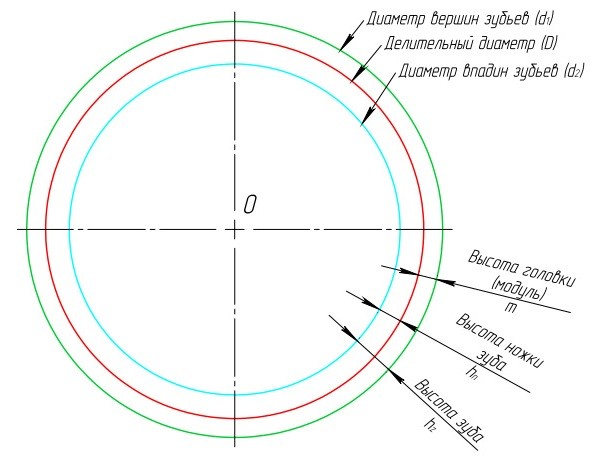
- Изобразите делительный диаметр с диаметром D, и центром шестерни O. Окружность показана красным цветом.
- Изобразите диаметр вершин зубьев (d1) с центром в точке O с радиусом большим на высоту головки зуба(зелёного цвета).
- Изобразите диаметр впадин зубьев (d2) с центром в точке O с радиусом меньшим на высоту ножки зуба (голубого цвета цвета).
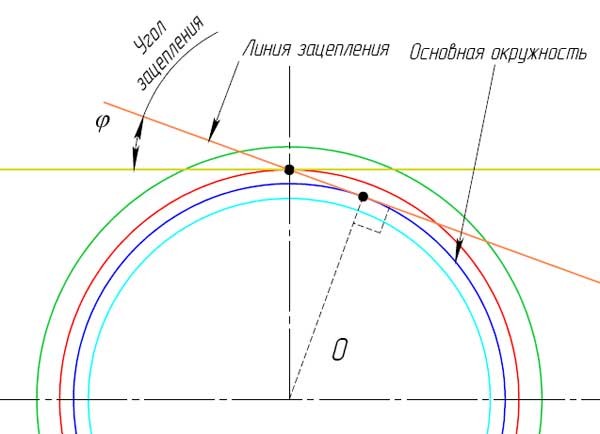
- Проведите касательную к делительному диаметру (желтая).
- В точке касания под углом ? проведите линию зацепления, оранжевого цвета.
- Изобразите окружность касательную к линии зацепления, и центром в точке O. Эта окружность является основной и показана тёмно синего цвета.
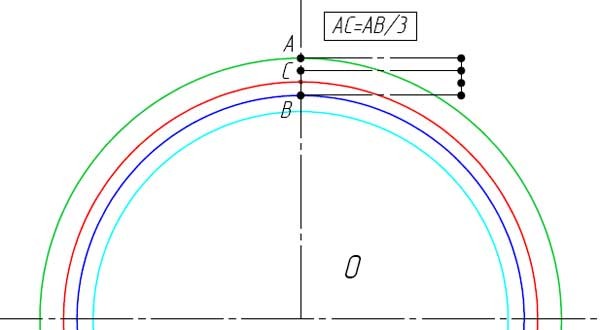
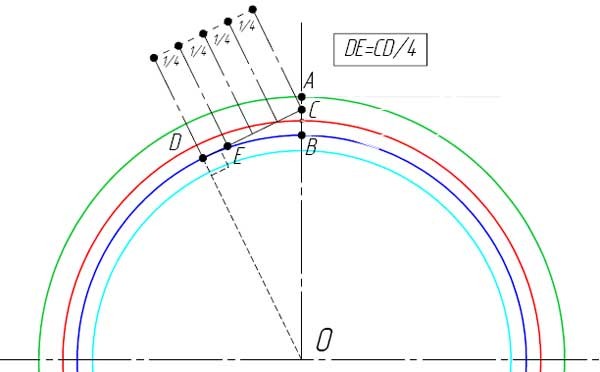
- От точки C проведите касательную к основной окружности.
- В точке касания отметьте точку D.
- Разделите расстояние DC на четыре части и отметьте, точкой E, полученное значение от точки D в сторону точки C на отрезке DC.
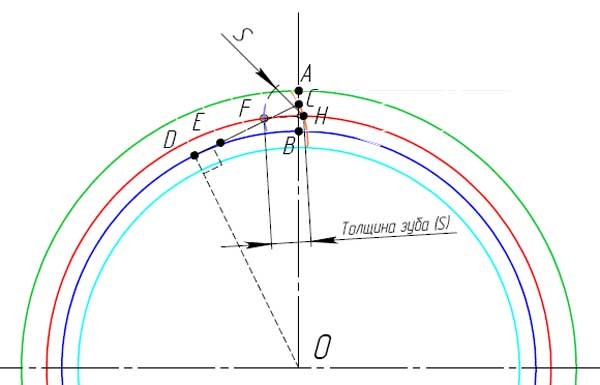
- Изобразите дугу окружности с центром в точке E, что проходит через точку C. Это будет часть одной стороны зуба, показана оранжевым.
- Изобразите дугу окружности с центром в точке H, радиусом, равным толщине зуба (s). Место пересечения с делительным диаметром отметьте точкой F. Эта точка находится на другой стороне зуба.
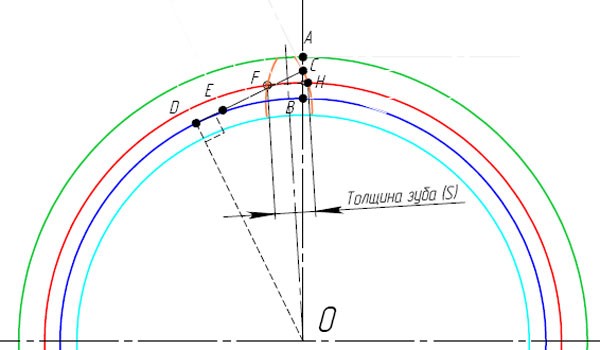
- Изобразите ось симметрии проходящую через центр О и середину расстояния FH.
- Линия профиля зуба отображенная зеркально относительно этой оси и будет второй стороной зуба.
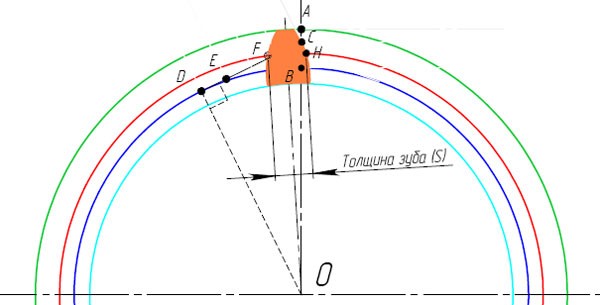
Вот и готов профиль зуба прямозубого зубчатого колеса. В этом примере использовались следующие параметры:
На этом первая часть урока является завершенной. Во второй части (видео) мы рассмотрим как применить полученный профиль зуба для построения модели зубчатого колеса. Для полного ознакомления с данной темой ("зубчатые колеса и зубчатые зацепления", а также "динамические сопряжения в SolidWorks") необходимо вместе с изучением этого урока изучать урок №24.
Еще скажу пару слов о специальной программе, производящей расчет зубчатых колес и генерацию модели зубчатого колеса для SolidWorks. Это программа Camnetics GearTrax.
Читайте также:


