Построить конус в excel

Обновлено: 07.01.2025

Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .

При попытке построить диаграмму типа Поверхность на основе одного ряда данных, MS EXCEL может сказать, что ему требуется как минимум 2 ряда. На самом деле, для более или менее наглядной поверхности потребуется как минимум 10 рядов (лучше 20 – для сложных поверхностей). К счастью, ряды не нужно создавать в ручную – достаточно правильно сформировать таблицу с исходными данными.

Построим график функции z=-sin(x*х+y*y)+1 (см. файл примера ).

В качестве источника данных используем таблицу, в которой в верхней строке указаны значения Х, а в левом столбце Y. В остальных ячейках – значения Z для всех пар (Х,Y)

Чтобы значения Z были более информативны - можно использовать Условное форматирование .

Условное форматирование показывает некий вариант изолиний (см. ниже): близкие значения Z выделены одним цветом. Это также позволяет предварительно оценить вид создаваемой диаграммы.

Теперь выделите любую ячейку таблицы и постройте диаграмму типа Поверхность (вкладка Вставка , группа Диаграммы , Кнопка Другие ).

Полученную фигуру можно повращать (кнопка Поворот объемной фигуры на вкладке Макет ).

Для построения диаграммы используется 3 оси: горизонтальная ось (категорий), вертикальная ось (значений), ось Z (рядов значений). Все 3 названия осей требуют пояснения.

Во-первых, ось Z на самом деле является нашей осью Х и отображает имена рядов. Если имена рядов убрать, то изменятся и подписи оси (убрать имена рядов можно нажав кнопку Изменить в окне Выбор источника данных , которое доступно через вкладку Конструктор ).

Этот факт роднит диаграмму Поверхность с Диаграммой График , где по Х отображаются лишь подписи. Т.е. при попытке построить поверхность с неравномерным шагом по Х (например, 1, 2, 5, 9, 77, 103, ..) получим искажения масштаба: значения по Х будут откладываться последовательно 1, 2, 3, … (конечно, Z будет рассчитаны правильно). Интересно, что формат подписей по оси Z можно настроить только изменяя формат ячеек, на которые ссылаются имена рядов (изменение формата на вкладке Число (в окне Формат Оси) ни к чему не приводит).

Во-вторых, по вертикальной оси (значений) на самом деле откладываются значения Z (это очевидно из рисунка).

И, наконец, в-третьих, горизонтальная ось (категорий) – это значения Y (на самом деле опять только подписи). Подписи, как и для Графика можно удалить или изменить нажав кнопку Изменить в окне Выбор источника данных , которое доступно через вкладку Конструктор (на этот раз нужно нажать кнопку расположенную справа).

Так как диаграмма Поверхность – это по сути трехмерный График , в котором одному Х соответствует один Y, то некоторые объемные фигуры отобразить на диаграмме Поверхность не удастся. Например, не удастся отобразить гиперболоид, т.к. каждой паре (Х;Y) на диаграмме Поверхность соответствует только один Z, а для гиперболоида это не так (каждой паре соответствует 2 значения Z). Поэтому, в MS EXCEL придется довольствоваться только половиной гиперболоида.

Как видно из диаграммы, близкие значения Z выделены одним цветом, которые указаны в Легенде. К сожалению, в MS EXCEL невозможно управлять этими уровнями (даже при повороте фигуры количество уровней и диапазоны значений существенно изменяются). Это приводит к тому, что построение изолиний ( линии уровня, контурный график, англ. Contour plot ) реализовано в MS EXCEL в достаточно ограниченном виде: невозможно указать на диаграмме значение изолинии (диапазоны цветов указаны на Легенде), разбиение на диапазоны по Z производится MS EXCEL автоматически и нет возможности на это повлиять. Ниже приведены изолинии для упомянутого выше гиперболоида. Это особый вид диаграммы – Проволочная контурная .

Практически такой же картинки можно добиться простым поворотом фигуры на диаграмме Поверхность .

Научимся строить изолинии (contour line) в MS EXCEL для одного из частных случаев поверхностей второго порядка: 2*a ₁₂ *x*y+2*a ₁₄ *x+ 2*a ₂₄ *y +2*a ₃₄ *z+a ₄₄ =0 . Изолинии в этом случае выражаются дробно-линейными функциями вида y=(a*x+b)/(c*x+d) .

В статье Изолинии в случае фигуры-плоскости в MS EXCEL было показано как построить изоляции для плоскости в трехмерном пространстве (плоскость задается уравнением A*X+B*Y+C*Z+D=0).

В этой статье построим изолинии (contour line) в MS EXCEL для одного из частных случаев поверхностей второго порядка: 2*a ₁₂ *x*y+2*a ₁₄ *x+2*a ₂₄ *y+2*a ₃₄ *z+a ₄₄ =0. Эта поверхность похожа на лист бумаги, у которого 2 угла загнуты вверх, а 2 вниз.

Примечание : В статье Трехмерные диаграммы (поверхности и изолинии) в MS EXCEL показано как построить изолинии для поверхности задаваемой функцией Z=-sin(X 2 +Y 2 )+1 с использованием штатных средств MS EXCEL: объемных диаграмм и Условного форматирования . Эти средства дают представления о форме изолиний, но имеют серьезные ограничения. Основное их преимущество состоит в простоте и скорости построения, а также универсальности (можно построить изолинии для любых поверхностей, если известно уравнение).

Изолинии для этой поверхности можно построить с помощью диаграммы типа Проволочная поверхность .

К сожалению, такая диаграмма имеет существенное ограничение - невозможно задать уровни изолиний, т.к. они рассчитываются автоматически.

В этой статье покажем как построить изолинии произвольного уровня для поверхности вида Z=A*X+B*Y+C*X*Y+D. Конечный результат будет выглядеть так:

Перед построением диаграммы исследуем уравнение поверхности. Это поможет нам построить изолинии и убережет от ошибок.

У данной поверхности есть особые точки, точнее 2 асимптоты: Х=-B/C и Y=-A/C.

Каждая изолиния состоит из двух частей (ветвей), расположенных в противоположных четвертях относительно асимптот. Мы будем их отображать одним цветом. Кроме того, для каждой ветви нам потребуется своя таблица с данными.

Исходные данные

Для построения диаграммы нам потребуется совсем не много исходных данных, а именно:

коэффициенты для задания уравнения поверхности: А, В, С и D;
начальное и конечное значение для Х и Y (можно задать начальное значение, количество точек и величину шага).

Алгоритм расчета точек изолиний

Рассчитываем координаты прямоугольника, ограничивающего область построения (выделен на диаграмме бордовым цветом). Диапазон А38:С43 ;
Вычисляем максимальное и минимальное значение Z для заданного диапазона значений Х и Y. Диапазон В19: В20 ;
Вычисляем значения для 10-и уровней изолиний (значение Z изменяется равномерно от минимального до максимального). Диапазон АI10: АI19 ;
Находим точки пересечения изолиний и прямоугольника, представляющего границу области определения. Если изолиния пересекает какую-либо сторону прямоугольника, то делает это только 1 раз. Каждая изолиния имеет 2 точки пересечения с прямоугольником: вход и выход, которые расположены на разных сторонах прямоугольника. Точка входа является первой точкой изолинии на диаграмме. Точка имеет координаты (Х;Y). Диапазон BR7: BY19 ;
Имея координаты точки входа и зная сторону прямоугольника, на которой она находится, вычисляем границы маленького квадратика (его стороны равны шагу по Х и по Y, т.е. ΔХ и ΔY, обычно равные). Маленький квадратик на диаграмме не отображается, он используется для вычисления точек изолинии. Диапазон S43:Z43 ;
Находим точку, в которой изолиния пересекает границы этого квадратика - это будет единственная точка, т.к. это следствие того, что мы выбрали именно такой тип поверхности. Эта точка будет следующей точкой диаграммы. Диапазон AF43:AI43 ;
Повторяем процедуру с маленьким квадратиком: точкой входа в него будет точка, вычисленная на предыдущем шаге. Процедура повторяется пока не будет достигнута граница области определения (бордовый прямоугольник);
Аналогично строится вторая ветвь изолинии (см. ячейку AN36 ). Для этого в отдельной таблице находится вторая точка входа (Диапазон BR23:BW33 ) и процедура с маленьким квадратиком повторяется.

Для построения одной ветви изолинии используется 40 точек. Если изолиния короткая, то может потребоваться меньше точек.

Как видно из приведенного выше алгоритма - процедура достаточно трудоемка. Кроме того, если необходимо изменить тип поверхности, например, гиперболический параболоид, то расчетные таблицы придется еще усложнить, т.к. в этом случае изолиния может пересекать одну сторону границы области определения сразу в 2-х точках. Но, если Вам требуется построить поверхность типа Z=A*X+B*Y+C*X*Y+D, то вышеуказанный алгоритм будет работать для любых коэффициентов А, В, С, D и для любых границ области определения.

Построение диаграммы

Изолинии в файле примера построены на диаграмме типа Точечная . Всего в диаграмме использовано 23 ряда:

9 февраля, 2014 Andrey K (30 голос, значение: 3,83 из 5)

Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.

1) Рассмотрим пример построения графика линейной функции: y=5x-2

Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку

В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.

В итоге мы получим табличку:

Теперь можно приступать к созданию графика.

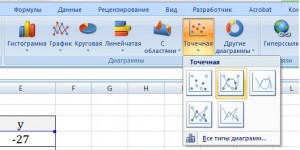
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ

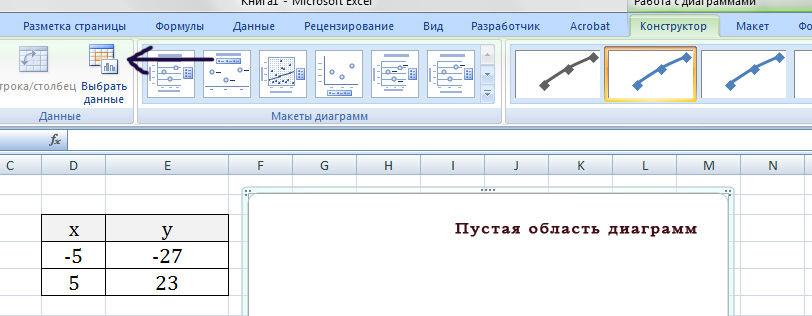
Нажимаем ОК. Перед нами график линейной функции.

Параболу по двум точкам уже не построить, в отличии от прямой.

Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу [-5; 5].

Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2.

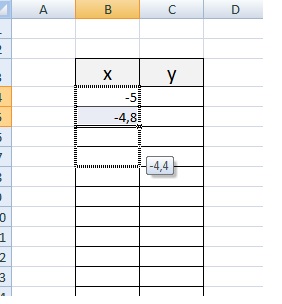
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.

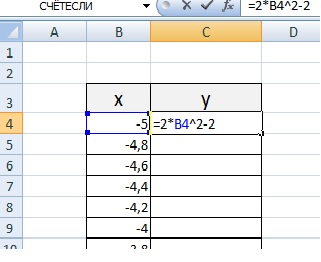
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.

Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.

Любые другие графики непрерывных функций строятся аналогично.

Рассмотрим это на примере функции у=1/х.

Функция определена на интервалах (- беск;0) и (0; +беск)

Создадим график функции на интервалах: [-4;0) и (0; 4].

Подготовим две таблички, где х изменяется с шагом 0,2:

Находим значения функции от каждого аргумента х аналогично примерам выше.

Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички

Получаем график функции y=1/x

Ячейки могут содержать данные трех типов:

Ввод формулы в ячейку необходимо начинать со знака =. В ячейке вместо правильного результата, финансирования при ее вычислении.

Формулы можно копировать, использую относительную и абсолютную адресацию . Относительный адрес доступа к помещению, исходя из ее расстояния до другого ячейки столбца или строки. При копировании формулы, хранящиеся адреса, эти адреса изменяются в соответствии с новым положением формулы.

Абсолютный адрес ячейки описывает ее точные координаты. При копировании формулы, сохраненный адрес, эти адреса не изменяются. Запись абсолютных адресов содержит знаки доллара ($ A $ 2). Можно использовать смешанные адреса, которые задают столбец относительно, а строку абсолютно, или наоборот (A $ 5, $ D3).

1.2.Типы диаграмм

В зависимости от типа диаграммы данные отображаются на ней разным способом.

Можно отметить несколько стандартных типов:

1. Гистограмма . В этом типе диаграмм данные отображаются в виде вертикальных или горизонтальных столбцов. Высота каждого столбца соответствует отображаемому значению. Если отображается несколько согласованных рядов, то столбцы либо строятся рядом, либо один над другим.

2. Линейчатая . Создание и настройка Линейчатой диаграммы аналогично Гистограмме. Различие состоит в том, что столбцы расположены не вертикально, а горизонтально.

3. График . Диаграмма График создана для отображения графиков функций (одному значению Х соответствует только одно значение Y). В этих диаграммах точки соединяются линиями.

4. С областями . Диаграмма с областями похожа на график.

5. Круговая диаграмма . В этом типе диаграмм величины отражаются секторами круга. Чем больше величина, тем большую долю круга занимает ее отображение.

Диаграмма Круговая не похожа на другие типы диаграмм, прежде всего потому, что формально в ней не используются Оси.

6. Точечная . Визуально Точечная диаграмма похожа на диаграмму типа График (если у Точечной диаграммы точки соединены линиями)

7. Поверхность . Диаграмма, в которой ряды становятся линиями для некоторой поверхности в объеме.

8. Лепестковая диаграмма . Каждый ряд отображается как линия, соединяющая точки на радиусах.

Подробнее о типах диаграмм здесь

1.3 Основы построения диаграмм в Excel

Чтобы создать диаграмму в MS Excel, сначала необходимо создать таблицу с исходными данными.
Для построения диаграммы необходимо как минимум один столбец (строка) числовых данных.
Необходимо выделить необходимый диапазон данных в таблице. Далее на вкладке Вставка в группе Диаграммы выбрать тип диаграммы.
Практически у всех типов диаграмм есть следующие элементы:
1. Название диаграммы
2. Область диаграммы
3. Область построения
4. Ряд данных (может быть несколько)
5. Подписи данных (для каждого ряда)
6. Легенда (нужна при наличии нескольких рядов данных, позволяет отличить разные наборы данных на диаграмме)
7. Оси (вертикальная, горизонтальная, вспомогательные). Осей нет у круговой диаграммы.

Совокупность этих элементов определяет макет диаграммы.

Для настройки макета существует отдельная вкладка Макет. В этой вкладке, а также на вкладке Формат есть группа Текущий фрагмент, с помощью которой можно быстро выделить нужный элемент.
Разберем основные элементы макета.
1. Название диаграммы. При создании диаграммы на основе таблицы с одним числовым столбцом, заголовок столбца автоматически становится названием диаграммы и именем ряда.
Выделить название диаграммы можно просто кликнув на него левой кнопкой мыши (или можно выбрать пункт Название диаграммы).

Дважды кликнув по Названию диаграммы левой клавишей мыши, будет выведено окно его свойств. Можно настроить отображение названия в нужном стиле.

Основные настройки также можно сделать через вкладку Формат, группа Стили фигур и Стили WordArt или через вкладку Главная, группа Шрифт.
2. Область диаграммы – это прямоугольник, на котором располагаются все остальные элементы диаграммы. Область диаграммы можно отформатировать по своему усмотрению
Для каждого типа диаграмм в MS EXCEL 2010 существуют заранее созданные стили.
Применение стиля коснется формата всех элементов макета (названия, области диаграммы, подписей данных, осей, области диаграммы и др.), даже если они в данный момент не выделены (в отличие от Стилей фигур на вкладке Формат, которые применяются только к выделенному элементу диаграммы).
3. Область построения . Настройка формата Области построения аналогична настройке формата Области диаграммы.
4. Ряды данных . Каждая диаграмма должна содержать хотя бы 1 Ряд данных. В зависимости от типа диаграммы отображение Ряда данных и его настройка будут различными.
Чтобы выделить Ряд данных, нужно кликнуть левой клавишей мыши по одному из столбцов гистограммы (или линии на диаграмме типа График, или по кругу на круговой диаграмме и т.д.) Также можно выбрать нужный Ряд в выпадающем списке, который находится в группе Текущий фрагмент на вкладке Макет или Формат.
Если Ряд данных выделен, то на листе также выделяется диапазон ячеек, содержащий источник данных. Настроить формат Ряда данных можно с помощью вкладки Формат или с помощью Окна свойств.
Чтобы удалить Ряд данных: кликните на нужный ряд данных и нажмите на клавиатуре клавишу DELETE. Если будет удален последний ряд, то вместе с ним удалятся Оси, Легенда и Область построения, но останется Область диаграммы.
5. Подписи данных . Чтобы отобразить подписи данных, необходимо выделить нужный ряд данных, а затем во вкладке Макет в группе Подписи выбрать нужный вариант размещения подписи.
Подписи данных, как правило, представляют собой значения из исходной таблицы, на основании которых и была построена диаграмма. Дважды кликнув на одну из подписей левой клавишей мыши можно вызвать диалоговое окно для настройки свойств подписи.
В качестве подписи можно установить не только само значение, но и имя ряда и имя категории (для Точечной диаграммы – значения Х).
В окне Формат подписей данных имеется вкладка Число, через которую можно настроить отображение числовых значений.
В случае необходимости можно индивидуально отредактировать подпись к определенной точке ряда.

6. Легенда . Полезна только при наличии нескольких рядов данных, т.к. позволяет отличить их на диаграмме.

Чтобы отобразить Легенду, необходимо во вкладке Макет в группе Легенда выбрать нужный вариант размещения. В том же меню доступно диалоговое окно Формат легенды для настройки свойств. Через тоже меню можно удалить Легенду (или нажать на клавиатуре клавишу DELETE).
В случае необходимости можно удалить из Легенды отображение имени определенного ряда.
7. Оси . При создании Гистограммы, Графика или Точечной диаграммы создаются горизонтальная и вертикальная оси (основные).

Конкретные параметры оси зависят от типа диаграммы и от типа оси (вертикальная или горизонтальная). Диалоговое окно свойств оси можно вызвать, выбрав пункт Горизонтальная ось или Вертикальная ось в выпадающем списке, который находится в группе Оси на вкладке Макет или Формат.
Можно создать Названия для осей и линии сетки по основным и вспомогательным значениям оси.
Если необходимо изменить источник данных или добавить новый ряд данных, то для этого выделите диаграмму, на вкладке Конструктор в группе Данные нажмите пункт Выбрать данные.

ГЛАВА 2. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

2.1 Уравнения поверхностей второго порядка и их графики

Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.

Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2+z^2/c^2=1, где a, b, c – полуоси эллипсоида.

Если a = b = c, имеем сферу (шар): x^2+y^2+z^2=a^2.

Эллиптическим параболоидом называется поверхность, которая в зависимости от типа канонического уравнения: x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = z.

Гиперболическим параболоидом называется поверхность, которая определяется в каноническом соотношении: x ^ 2 / a ^ 2-y ^ 2 / b ^ 2 = z. Ввиду геометрической схожести гиперболический параболоид часто называют «седлом».

2.2. Построение поверхностей второго порядка в Excel

Для построения шаблонов в Excel необходимо использовать диаграммы типа Поверхность и уметь работать с относительными и абсолютными адресами ячеек.
Для построения следующего порядка:
1. Из уравнения второй порядка выразить переменную z.
2. Подготовить изменения функций по двум координатам и другим направлениям, а также другим направлениям вдоль прилегающей строки вправо.
3. Ввести на пересечении геометрия для построения поверхности (и использовать марксист автозаполнения для ее копирования на всю область построения поверхности.
4. Выделить подготовленные данные и построить диаграмму типа Поверхность (вкладка Вставка, группа Диаграммы, Кнопка Другие).
4. Отформатировать полученную поверхность. Полученную фигуру можно вращать (кнопка Поворот объемной фигуры на вкладке Макет).
Для осуществления рассмотренного построения, заданной формулой:
x ^ 2 + y ^ 2 + z ^ 2 = 1
Для построения:
1. Выразим z: z = √ (x ^ 2 + y ^ 2-1)
2. Зададим диапазон С3: AR3 для x от -1 до 1 с шагом 0,1, причем каждое значение дублируется последовательно. Аналогично вводятся значения у для диапазона B4: B45.
3. Для расчёта z при изменяющихся x и y в ячейку С4 введем формулу:
= КОРЕНЬ (1-C $ 3 ^ 2- $ B4 ^ 2) * ЕСЛИ (ОСТАТ ($ A4; 2) = 0; 1; -1).
4. В диапазоне A4: A45 введем повторяющиеся числа 2 и 3 для определения знака в формуле.
5. Выделил подготовленные данные и построил диаграмму типа Поверхность.

6. Отформатируем полученную поверхность как показано на рисунке.

Для наиболее наглядного и полного отображения фигуры необходимо подбирать область и шаг изменения величины x и y.

Читайте также: