Построить эллипсоид в excel
1. Построить верхнюю (четные варианты) или нижнюю (нечетные варианты) часть эллипсоида, заданного уравнением . Варианты заданий представлены в табл. 6.
2. Построить однополостный (четные варианты) или двухполостный (нечетные варианты) гиперболоид, заданный уравнением . Знак плюс относится к уравнению однополостного гиперболоида, знак минус – к уравнению двухполостного гиперболоида. Варианты заданий представлены в табл. 7.
3. Построить эллиптический (четные варианты) или гиперболический (нечетные варианты) параболоид, заданного уравнением . Знак плюсотносится к уравнению эллиптического параболоида, знак минус – к уравнению гиперболического параболоида. Варианты заданий представлены в табл.8.
Таблица 6. Варианты заданий
| № | a | b | с | № | a | b | c |
| 3.1 | 3.2 | 5.3 | |||||
| 0.9 | 1.1 | 1.25 | 1.95 | 1.5 | |||
| 1.5 | 1.25 | 1.95 | |||||
| 0.71 | 0.75 | 1.21 | |||||
| 1.72 | 2.9 | 3.1 | |||||
| 5.71 | 4.75 | 4.21 | 7.1 | 7.5 | 4.21 | ||
| 2.72 | 3.9 | 5.1 | 7.2 | 8.9 | |||
| 1.5 | 0.78 | 1.45 | 1.5 | 2.78 | 3.45 |
Таблица 7. Варианты заданий
| № | a | b | с | № | a | b | c |
| 3.1 | 3.2 | 5.3 | |||||
| 0.9 | 1.1 | 1.25 | 1.95 | 1.5 | |||
| 1.5 | 1.25 | 1.95 | |||||
| 0.71 | 0.75 | 1.21 | |||||
| 1.72 | 2.9 | 3.1 | |||||
| 5.71 | 4.75 | 4.21 | 7.1 | 7.5 | 4.21 | ||
| 2.72 | 3.9 | 5.1 | 7.2 | 8.9 | |||
| 1.5 | 0.78 | 1.45 | 1.5 | 2.78 | 3.45 |
Таблица 8. Варианты заданий
| № | p | q | № | p | q |
| 1.5 | 2.5 | ||||
| 2.5 | 1/5 | ||||
| 1.4 | 3.4 | ||||
| 3.4 | 1.4 | ||||
| 2.5 | 5.6 | ||||
| 5.4 | 2/5 | ||||
| 1.1 | 4.1 | ||||
| 4.1 | 1.2 | ||||
| 1.5 | 5.1 | ||||
| 5.5 | 1.5 | ||||
| 3.3 | 5.3 | ||||
| 5.1 | 3.7 | ||||
| 4.1 | 5.1 | ||||
| 5.3 | 4.2 | ||||
| 6.05 | 1.9 |
Рекомендации к выполнению лабораторной работы.
ПРИМЕР 1. Построить поверхность z=x 2 -y 2 при x, y Î[-1;1].
В диапазон B1:L1 введем последовательность значений переменной x: -1, -0.8, …,1, а в диапазон ячеек А2:А12 последовательность значений переменой y. В ячейку В2 введем формулу =$A2^2-B$1^2. Знак $, стоящий перед буквой в имени ячейки, дает абсолютную ссылку на столбец с данным именем, а знак $, стоящий перед цифрой – абсолютную ссылку на строку с этим именем. Поэтому при копировании формулы из ячейки В2 в ячейки диапазона B2:L12 в них будет найдено значение z для соответствующих значениях x, y. Таким образом, будет создана таблица значений z.
Для построения поверхности выделим диапазон ячеек A1:L12, содержащий таблицу значений функции. Далее обратимся к Мастеру диаграммивыберемтип диаграммы Поверхность. Затем заполним диалоговые окна в соответствии с вариантом задания и получим трехмерный график, показанный на рис 15.
Рис.15. Поверхность вида z=x 2 -y 2
ПРИМЕР 2. Построить верхнюю часть эллипсоида, заданного уравнением .
Выразим z через x и y.
Выражение описывает верхнюю часть эллипсоида.
Найдем область определения функции z(x,y).
Выполним построения как в предыдущем примере (рис. 16).
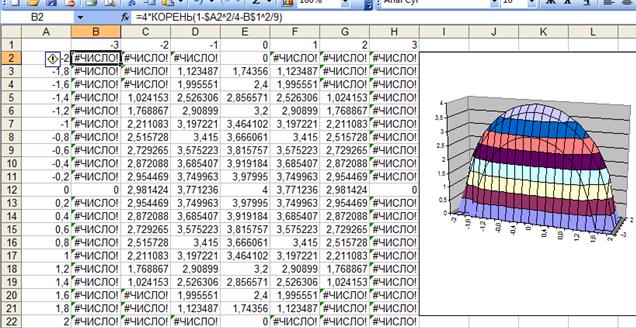
ПРИМЕР 3. Построить двухполосный гиперболоид, заданный уравнением .
Выразим z через x и y.
Функция определена везде. Выполним построения (рис. 17).
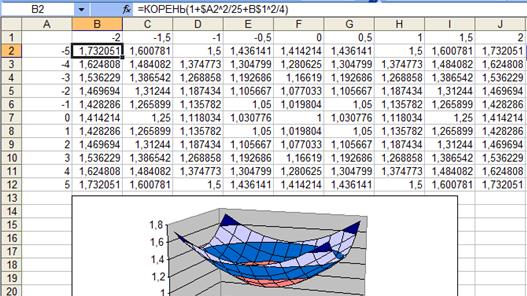
ПРИМЕР 3. Построить однополосный гиперболоид, заданный уравнением .
Выразим z через x и y.
Выражение описывает однополосный гиперболоид.
Найдем область определения функции z(x,y).
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:
Это уравнение называется каноническим уравнением эллипсоида.
Эллипсоид представляет собой замкнутую овальную поверхность, обладающую тремя взаимно перпендикулярными плоскостями симметрии.
Для построения эллипсоида в Excel каноническое уравнение (7.7) необходимо разрешить относительно переменной z (представить в виде z=f(x, у)).
Упражнение 8.2.Рассмотрим построение эллипсоида в Excel на примере уравнения:
Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: хÎ[–3; 3], уÎ[–2; 2] с шагом D=0,5 для обеих переменных.
Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере
Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ х. В ячейку А2 вводится первое значение аргумента — левая граница диапазона (–3). В ячейку A3 вводится второе значение аргумента — левая граница диапазона плюс шаг построения (–2,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).
Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (–2). В ячейку С1 вводится второе значение переменной — левая граница диапазона плюс шаг построения (–1,5). Затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки J1).
(при х=–3 и у=–2 точек рассматриваемого эллипсоида не существует).
Теперь необходимо скопировать функцию из ячейки В2. Для этого автозаполнением (протягиванием вправо) копируем эту формулу вначале в диапазон B2:J2, после чего (протягиванием вниз) — в диапазон ВЗ:J14.
В результате должна быть получена следующая таблица точек эллипсоида.
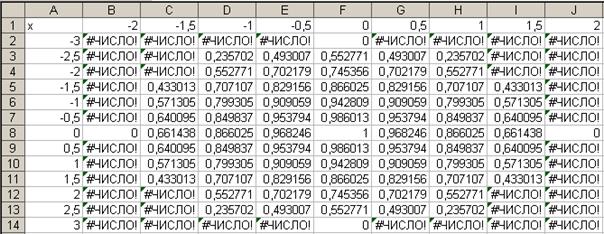
Для построения диаграммы на панели инструментов Стандартная необходимо нажать кнопку Мастер диаграмм. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы указываем тип диаграммы — Поверхность, и вид — Проволочная (прозрачная) поверхность (правую верхнюю диаграмму в правом окне). После чего нажимаем кнопку Далее в диалоговом окне.
В появившемся диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку Диапазон данных и в поле Диапазон мышью указать интервал данных B2:J14.
Далее необходимо указать в строках или столбцах расположены ряды данных. Это определит ориентацию осей х и у. В примере переключатель Ряды в с помощью указателя мыши установим в положение столбцах.
Выбираем вкладку Ряд и в поле Подписи оси X указываем диапазон подписей. Для этого щелкните в нем указателем мыши и введите диапазон подписей оси х — А2: A14.
Вводим значения подписей оси у. Для этого в рабочем поле Ряд указываем первую запись Ряд 1 иврабочее поле Имя, активизировав его указателем мыши, вводим первое значение переменной у: –2. Затем в поле Ряд указываем вторую запись Ряд 2 и в рабочее поле Имя вводим второе значение переменной у: –1,5. Повторяем таким образом до последней записи — Ряд 9.
После появления требуемых записей необходимо нажать кнопку Далее.
В третьем окне требуется ввести заголовок диаграммы и названия осей. Для этого необходимо выбрать вкладку Заголовки, щелкнув на ней указателем мыши. Щелкнув в рабочем поле Название диаграммы указателем мыши, ввести с клавиатуры в поле название: Эллипсоид. Затем аналогичным образом ввести в рабочие поля Ось X (категорий), Ось Y (рядов данных) и Ось Z (значений) соответствующие названия: х, у и z.

Далее следует нажать кнопку Готово, и после небольшого редактирования будет получена следующая диаграммаэллипсоида.
Читайте также:


