Напишите программу которая обнуляет заданное количество последних бит числа java
Переменные типа int хранятся в двоичной системе счисления в виде последовательности бит. Биты нумеруются от 0, биты будем записывать справа налево (то есть бит с номером 0 будет записан самым правым, а самый старший бит — самым левым).
Например, если a = 10 , то в битовой записи a биты с номерами 1 и 3 равны 1, а остальные биты равны 0.
В программах на языке Питон числа в двоичной системе счисления можно записывать в виде последовательностей из 0 и 1, предваряя их префиксом 0b . Например, допустимо присваивание a = 0b101 .
Для двух переменных одинакового скалярного типа определены битовые операции:
& битовое И (AND)
| битовое ИЛИ (OR)
^ битовое ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR)
битовое ОТРИЦАНИЕ (NOT) — унарная операция.
Битовые операторы работают следующим образом. Берутся два операнда, и к каждой паре соответствующих бит для левого и правого операнда применяется данная операция, результатом будет переменная того же типа, каждый бит которой есть результат применения соответствующей логической операции к соответствующим битам двух операндов. Рассмотрим пример:
Битовое отрицание числа (величина f в последнем примере) — это число, полученное из исходного заменой всех нулей на единицы и наоборот.
Применение побитового отрицания к неотрицательному числу даст отрицательное число, что связано с особенностями представления отрицательных чисел в виде дополнительного кода.
Есть еще две операции, работающие с битами: это битовые сдвиги. Их два: сдвиг влево и вправо. Оператор a >> n возвращает число, которое получается из a сдвигом всех бит на n позиций вправо, при этом самые правые n бит отбрасываются. Например:
Понятно, что для положительных чисел битовый сдвиг числа вправо на n равносилен целочисленному делению на 2 n . Для отрицательных чисел в языке Питон операции битового сдвига неприменимы.
Аналогично, битовый сдвиг влево на n бит равносилен (для положительных чисел) умножению на 2 n и осуществляется при помощи оператора << :
Упражнения
Во всех упражнениях (если не оговорено иное) нельзя использовать арифметические операторы сложения, умножения, вычитания, деления, взятия остатка. Вместо них используем побитовые операторы & , | ,
A: 2 k
Дано число k, 0≤k≤31. Запишите число 2 k , то есть число, у которого k-й бит равен 1, а остальные — нули.
| Ввод | Вывод |
|---|
B: 2 k +2 n
Даны два неравных целых неотрицательных числа: k и n. Вычислите 2 k +2 n .
| Ввод | Вывод |
|---|
C: Обнулить последние биты
Дано целое число A и целое неотрицательное число число k. Обнулите у числа A его последние k бит и выведите результат.
| Ввод | Вывод |
|---|
D: Установить бит
Дано целое число A и целое неотрицательное число k. Выведите число, которое получается из числа A установкой значения k-го бита равному 1.| Ввод | Вывод |
|---|
E: Инвертировать бит
Дано целое число A и целое неотрицательное число k. Выведите число, которое получается из числа A инвертированием k-го бита.| Ввод | Вывод |
|---|
F: Значение бита
Дано целое число A и целое неотрицательное число k. Выведите значение k-го бита числа A, то есть 0 или 1.| Ввод | Вывод |
|---|
G: Обнулить бит
Дано целое число A и целое неотрицательное число k. Выведите число, которое получается из числа A установкой значения k-го бита равному 0.| Ввод | Вывод |
|---|
H: Обрезать старшие биты
Дано целое число A и натуральное число k. Выведите число, которое состоит только из k последних бит числа A (то есть обнулите все биты числа A, кроме последних k).| Ввод | Вывод |
|---|
I: Битовое представление
Дано натуральное число. Выведите его битовое представление.
В этой задаче можно использовать циклы, но нельзя использовать операции деления и умножения, а также функции bin и т.д.
| Ввод | Вывод |
|---|
J: Быстрое вычисление
Даны числа \(a\) и \(b\). Используя только битовые операции и операции сложения и вычитания вычислите число \(x = (18a + [\frac]) \bmod 32\). Выведите результат на экран.
| Ввод | Вывод |
|---|
K: Быстрое умножение
Даны числа \(a\) и \(b\). Не используя операции * , / , // , % вычислите их произведение.
| Ввод | Вывод |
|---|
L: Заменить 1 на 0
Дано число, замените первую справа единицу его двоичной записи на ноль.
Разрешается использовать битовые и арифметические операции. Запрещается использовать ветвления и циклы.
| Ввод | Вывод |
|---|
M: Замените 0 на 1
Дано число, замените первый справа ноль его двоичной записи на единицу.
Разрешается использовать битовые и арифметические операции. Запрещается использовать ветвления и циклы.
| Ввод | Вывод |
|---|
N: Шифрование перемешиванием
Дано число, переставьте его соседние биты (то есть поменяйте местами биты с номерами 0 и 1, 2 и 3, 4 и 5 и т.д.). Разрешается использовать битовые операции. Запрещается использовать арифметические операции, ветвления, циклы.
Общее число бит в числе не превосходит 32.
O: Из дополнительного кода
Поскольку в языке Питон встроенная целочисленная арифметика является длинной, то создается иллюзия того, что целые числа имеют бесконечное число разрядов. При этом у положительных чисел лидирующие разряды в двоичной системе счисления заполнены битом 0, а у отрицательных чисел — битом 1. Этот факт мы будем записывать следующим образом: символы “ 0
” будут обозначать бесконечное число нулевых бит, а символы “ 1
” бесконечное число единичных бит. То есть число 5 в дополнительном коде мы будем записывать, как 0
101 , а число -5 как 1
При этом бит, следующий после знака
должен отличаться от бита, идущего до него, то есть запись 0
11011 считается неправильной. Исключениями являются числа 0 (записывается как 0
0 ) и -1 (записыватеся как 1
Дана запись ненулевого числа в дополнительном коде, в соответствии с указанным выше форматом. Определите значение записанного числа.
| Ввод | Вывод |
|---|
P: В дополнительный код
Решите задачу, обратную предыдущей.
Q: Контрольная сумма BSD
В операционной системе BSD используется следующий алгоритм вычисления контрольных сумм.
Контрольная сумма хранится в двубайтовой целочисленной переменной \(h\) (то есть хранятся только два байта числа, все вычисления выполняются в кольце вычетов по модулю \(2^\). С самого начала эта переменная равна 0.
Далее с каждым считанным байтом \(c\) выполняются следующие операции.
Значение \(h\) циклически сдвигается вправо (то есть последний бит становится первым, не забываем, что число \(h\) является 16-битным. К значению \(h\) прибавляется значение считанного байта (то есть ASCII-кода его), от результата берется последние 16 бит.
Вот пример вычисления контрольной суммы для строки “AND“
Результат равен 16507. Обратите внимание, что после сложения результат может оказаться более чем 16-битным, и требуется оставить только последние 16 бит.
В системе Linux можно проверить результат работы при помощи консольной команды sum :
| Ввод | Вывод |
|---|
R: Adler-32
В алгоритме Adler-32 вычисляются две 16-битные суммы: A — сумма всех байт входных данных и B — сумма всех промежуточных значений суммы A. При этом начальное значение A инициализируется числом 1, а начальное значение B — числом 0. Все вычисления проводятся по модулю 65521 (максимальное простое, меньшее \(2^\)).
Таким образом, если файл состоит из байт \(d_1\), \(d_2\), . \(d_n\), то \(A = 1 + d_1 + d_2 + . + d_n \bmod 65521\), \(B = (1 + d_1) + (1 + d_1 + d_2) + . + (1 + d_1 + . + d_n) \bmod 65521\).
Итоговым значением контрольной суммы является одно 32-битное число, в котором в старших 16 битах записано значение B, в младших 16 битах - значение A.
Вычислите контрольную сумму Adler-32 для данной строки.
| Ввод | Вывод |
|---|
S: FNV-1 хеш-функция
Алгоритм хеширования FNV-1 устроен следующим образом. Используется 64-битная арифметика. Переменная \(h\) хранит текущее значение хеш-функции. Начальное значение \(h\) равно 14695981039346656037. На каждом шаге значение \(h\) домножается на 1099511628211, затем делается побитовое исключающее ИЛИ с очередным байтом входных данных. Все вычисления проводятся с 64-битными целыми числами, поэтому после выполнения всех операций нужно брать младшие 64 бита результата.
Вычислите значение хеш-функции FNV-1 для данной строки.
| Ввод | Вывод |
|---|
T: PJW-32 хеш-функция
1. Значение \(h\) сдвигается на 4 бита влево, к нему прибавляется (арифметическим суммированием) значение \(c\).
2. Если хотя бы один из 4 старших битов \(h\) равен 1, то старшие 4 бита сдвигаются на 24 бита вправо, и выполняется операция побитового исключающего ИЛИ со значением \(h\). После чего обнуляются старшие 4 бита значения \(h\).
Все операции проводятся с 32-битными числами, то есть берутся 32 младших бита результата.
| Ввод | Вывод |
|---|
Z*: SHA-1
SHA-1 — алгоритм, вычисляющий криптографические контрольные суммы от произвольной битовой последовательности. Результатом вычисления функции SHA-1 является 160-битный хэш, который как правило записывается в виде 40 16-ричных цифр. Хэш-функция является односторонней, то есть по значению хэш-функции тяжело подобрать какую-либо исходную последовательность, имеющую такое значение хэш-функции.
Изучите описание алгоритма вычисления контрольной суммы SHA-1 по материалам википедии и реализуйте данный алгоритм.
Программа получает на вход одну строку и должна вывести значение SHA-1 суммы для этой строки. Исходная последовательность байт для вычисления SHA-1 суммы состоит только из символов этой строки, так в примере ниже входная строка имеет длину 3 байта = 24 бита. Добавлять к строке символ \n и иные спецсимволы не нужно.
Программа должна вывести 40 16-ричных цифр, цифры a - f записываются в строчном регистре.
| Ввод | Вывод |
|---|
Для тестирования можно использовать стандартную команду sha1sum из дистрибутива Linux. Например, ответ на тест из условия получен при помощи команды echo -n "sha" | sha1sum .
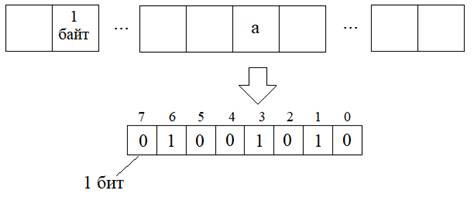
В свою очередь байт состоит из 8 бит. Бит – это элементарная ячейка памяти, которая может принимать только два значения: 0 и 1. И каждый бит имеет свой номер от младшего 0 – до старшего 7. Так вот, все целочисленные значения переменной a можно представить в виде последовательности из 8 бит. Например, значение, что изображено на рисунке соответствует десятичному числу

А общее число вариантов равно

Именно поэтому переменная типа byte может содержать числа
всего 256 вариантов. Причем признаком отрицательного числа является старший бит, установленный в 1. Например, вот такое число в битовом представлении
чему равно? Для этого нам надо инвертировать вот эти младшие 7 бит, вычислить его десятичное представление и прибавить 1. Получим:
значит, это отрицательное число -128. А вот если взять такое:
то после инверсии 7 младших бит, имеем:
значит, это число -1. Вот так кодируются отрицательные числа на уровне бит. И это работает не только в Java – это общепринятая кодировка чисел через биты.
Итак, язык Java имеет операторы, позволяющие менять отдельные биты переменных. Основными из них являются:
И, ИЛИ, НЕ, исключающее ИЛИ (XOR)
Битовая операция НЕ
Начнем с самой простой битовой операции НЕ, которая выполняет инверсию бит в соответствии с такой табличкой:
На языке Java она записывается как
тильда. И приведем такую программу.
Здесь мы сначала задаем переменную var со значением 121, затем, выполняем ее побитовую инверсию, и выводим результат на экран.
Запустим программу и видим на экране число -122, что и должно быть, так как инверсия последних 7 бит дает
значит, это число -122.
Битовая операция И
Далее рассмотрим операцию поразрядное И. На Java она записывается как & и для ее работы нужны уже два числа или две переменные, например, так.
то есть, смотрите что получается. В соответствии с таблицей истинности результирующие биты будут следующими. (перечислить). В итоге, переменная res будет равна 4. Запустим программу и убедимся, что это так.
Ну хорошо, разобрались, но зачем все это надо? Смотрите, если нам нужно проверить включен ли какой-либо бит числа (то есть установлен в 1), то мы можем это сделать с помощью битовой операции И следующим образом:
Для проверки мы здесь использовали оператор if, о котором подробно поговорим на следующем занятии. Интерпретировать здесь его следует так: если вот эта битовая операция по числовому значению будет равна mask, то выполняется вот эта конструкция, иначе – вот эта.
И теперь смотрите, мы здесь задали маску, у которой 2-й бит установлен в 1. Тогда в соответствии с операцией И у нас в результате все биты обнулятся, кроме 2-го, но только в том случае, если в переменной flags он установлен в 1. Давайте запустим программу и убедимся, что все работает.
И для проверки поменяем переменную flags на 1
и проверим что будет. Да, все верно, выводится что 2-й бит выключен. Вот так мы проверили включен или нет 2-й бит. По аналогии можно проверять и другие биты или сразу группы бит.
Другим важным назначением операции И является выключение определенных бит переменной. Это делается так.
Что происходит здесь? Сначала выполняется инверсия бит маски, так как операция НЕ имеет более высокий приоритет, чем операция И. Получаем, что маска состоит из вот таких бит. Затем, идет операция поразрядное И, и там где в маске стоят 1 биты переменной flags не меняются, остаются прежними, а там где стоят в маске 0 – эти биты в переменной flags тоже становятся равными 0. За счет этого происходит выключение 2-го и 0-го битов переменной flags.
В этом уроке мы увидим, как мы можем использовать BitSet s для представления вектора битов.
Во-первых, мы начнем с обоснования отказа от использования boolean[] . Затем, после ознакомления с BitSet internals, мы более подробно рассмотрим его API.
2. Массив битов
Для хранения и манипулирования массивами битов можно утверждать, что мы должны использовать boolean[] в качестве структуры данных. На первый взгляд это может показаться разумным предложением.
Однако каждый член boolean в boolean[] обычно потребляет один байт вместо одного бита . Поэтому, когда у нас жесткие требования к памяти или мы просто стремимся к сокращению объема памяти, boolean[] далеки от идеала.
Чтобы сделать вопрос более конкретным, давайте посмотрим, сколько места занимает boolean[] с 1024 элементами:
В идеале мы ожидаем 1024-битный объем памяти от этого массива. Однако Макет объекта Java (JOL) показывает совершенно иную реальность:
Если мы проигнорируем накладные расходы заголовка объекта, элементы массива потребляют 1024 байта вместо ожидаемых 1024 бит. Это на 700% больше памяти, чем мы ожидали.
Проблемы адресуемости и разрыв слов являются основными причинами, по которым boolean s-это больше, чем просто один бит.
Для решения этой проблемы мы можем использовать комбинацию числовых типов данных (например, long ) и побитовых операций. Вот тут-то и появляется набор битов /.
3. Как работает битовый набор
Как мы уже упоминали ранее, для достижения одного бита на использование памяти флага API BitSet использует комбинацию основных числовых типов данных и битовых операций.
Для простоты предположим, что мы собираемся представить восемь флагов с одним байтом . Сначала мы инициализируем все биты этого единственного байта нулем:
Теперь, если мы хотим установить бит в позиции три в true , мы должны сначала сдвинуть число 1 влево на три:
А затем или его результат с текущим байтом значением :
Тот же процесс произойдет, если вы решите установить бит в индексе семь:
Как показано выше, мы выполняем сдвиг влево на семь битов и объединяем результат с предыдущим значением byte с помощью оператора или .
3.1. Получение битового индекса
Чтобы проверить, установлен ли конкретный битовый индекс в true или нет, мы будем использовать оператор и //. Например, вот как мы проверяем, установлен ли индекс три:
- Выполнение сдвига влево на три бита по значению один
- И в результат с текущим байтом значением
- Если результат больше нуля, то мы нашли совпадение, и этот битовый индекс фактически установлен. В противном случае запрашиваемый индекс является чистым или равен false
На приведенной выше диаграмме показаны шаги операции get для третьего индекса. Однако, если мы спросим о четком индексе, результат будет другим:
Поскольку результат end равен нулю, индекс четыре ясен.
3.2. Выращивание хранилища
В настоящее время мы можем хранить только вектор из 8 бит. Чтобы выйти за пределы этого ограничения, нам просто нужно использовать массив байт s, а не один байт , вот и все!
Теперь каждый раз, когда нам нужно установить, получить или очистить определенный индекс, мы должны сначала найти соответствующий элемент массива. Например, предположим, что мы собираемся установить индекс 14:
Как показано на приведенной выше диаграмме, после нахождения правильного элемента массива мы установили соответствующий индекс.
Кроме того, если мы хотим установить здесь индекс выше 15, то BitSet сначала расширит свой внутренний массив. Только после расширения массива и копирования элементов он установит запрошенный бит. Это несколько похоже на то, как ArrayList работает внутренне.
До сих пор мы использовали тип данных byte для простоты. Битовый набор API, однако, использует массив long значений внутри .
4. API набора бит
Теперь, когда мы достаточно знаем о теории, пришло время посмотреть, как выглядит API BitSet .
Для начала давайте сравним объем памяти экземпляра BitSet с 1024 битами с boolean [] , который мы видели ранее:
Это приведет к печати как мелкого размера экземпляра BitSet , так и размера его внутреннего массива:
Как показано выше, он использует long[] с 16 элементами (16 * 64 бита) внутри. В любом случае, этот экземпляр использует в общей сложности 168 байт, в то время как boolean[] использовал 1024 байта .
Чем больше у нас битов, тем больше увеличивается разница в следах. Например, для хранения 1024 * 1024 бит boolean[] потребляет 1 МБ, а экземпляр BitSet потребляет около 130 КБ.
4.1. Построение битовых наборов
Самый простой способ создать экземпляр BitSet -использовать конструктор no-arg :
Это создаст экземпляр BitSet с long[] размером один . Конечно, при необходимости он может автоматически увеличить этот массив.
Здесь во внутреннем массиве будет достаточно элементов, чтобы вместить 100 000 бит. Этот конструктор пригодится, когда у нас уже есть разумная оценка количества битов для хранения. В таких случаях использования он может предотвратить или уменьшить ненужное копирование элементов массива при его увеличении|/.
Можно даже создать BitSet из существующего long[] , byte[] , Long Buffer и ByteBuffer . Например, здесь мы создаем экземпляр BitSet из заданного long[] :
Существует еще три перегруженных версии метода value Of() static factory для поддержки других упомянутых типов.
4.2. Установка битов
Мы можем установить значение определенного индекса в true с помощью метода set(index) |/:
Как обычно, индексы основаны на нуле. Можно даже установить диапазон битов в true с помощью set(fromInclusive, toExclusive) |/метод :
Как видно из подписи метода, начальный индекс является включающим, а конечный-исключающим.
Эта версия также поддерживает настройку диапазона значений:
4.3. Очистка битов
Вместо того , чтобы устанавливать определенный битовый индекс в false , мы можем просто очистить его с помощью метода clear(index) |/:
Кроме того, мы также можем очистить диапазон битов с помощью clear(от Inclusive до Exclusive) перегруженной версии:
Интересно, что если мы вызовем этот метод без передачи каких-либо аргументов, он очистит все заданные биты :
Как показано выше, после вызова метода clear() все биты равны нулю.
4.4. Получение битов
До сих пор мы довольно широко использовали метод get(index) . Когда задан запрошенный битовый индекс, этот метод вернет true . В противном случае он вернет false :
Аналогично set и clear , мы можем получить диапазон битовых индексов с помощью метода get(fromInclusive, toExclusive) :
Как показано выше, этот метод возвращает другой Набор битов в диапазоне [20, 30) текущего. То есть индекс 20 переменной BitSet эквивалентен нулевому индексу переменной new BitSet .
4.5. Переворачивание битов
Чтобы отрицать текущее значение битового индекса, мы можем использовать метод flip(index) |///. То есть он превратит true значения в false и наоборот:
Аналогично, мы можем достичь того же самого для диапазона значений, используя метод flip(fromInclusive, toExclusive) :
4.6. Длина
Существует три метода, подобных длине, для набора битов . Метод size() возвращает количество битов, которые может представлять внутренний массив . Например, поскольку конструктор no-arg выделяет массив long[] с одним элементом, то size() вернет для него 64:
С одним 64-битным числом мы можем представлять только 64 бита. Конечно, это изменится, если мы передадим количество битов явно:
Кроме того, метод cardinality() представляет количество битов набора в наборе битов :
Сначала этот метод возвращает ноль, так как все биты false . После установки диапазона [10, 30) в true вызов метода cardinality() возвращает 20.
Кроме того, метод length() возвращает один индекс после индекса последнего установленного бита :
Сначала последний заданный индекс равен 29, поэтому этот метод возвращает 30. Когда мы устанавливаем индекс 100 в значение true, метод length() возвращает 101. Также стоит упомянуть, что этот метод вернет ноль, если все биты чисты .
Наконец, метод isEmpty() возвращает false , когда в наборе битов имеется хотя бы один бит набора . В противном случае он вернет true :
4.7. Объединение С Другими Наборами Битов
Метод intersects(BitSet) принимает другой BitSet и возвращает true при двух Набор битов s имеет что-то общее . То есть у них есть по крайней мере один бит набора в одном и том же индексе:
Диапазон [7, 9] задан в обоих BitSet s, поэтому этот метод возвращает true .
Также можно выполнить логическую операцию и на двух Набор битов s :
Это выполнит логическое и между двумя BitSet s и изменит первую переменную с результатом. Аналогично, мы можем выполнить логическое xor на двух Битный набор s тоже:
Существуют и другие методы, такие как andNot(BitSet) или или(Bit Set) , , которые могут выполнять другие логические операции над двумя BitSet s.
4.8. Разное
Начиная с Java 8, существует метод stream () |/для потоковой передачи всех битов набора BitSet . Например:
Это выведет все установленные биты на консоль. Поскольку это вернет IntStream , мы можем выполнять обычные числовые операции, такие как суммирование, усреднение, подсчет и так Далее. Например, здесь мы подсчитываем количество установленных битов:
Кроме того, метод nextSetBit(fromIndex) вернет следующий битный индекс набора, начиная с fromIndex :
Сам fromIndex включен в этот расчет. Когда в наборе BitSet не осталось ни одного бита true , он вернет значение -1:
Аналогично, | nextClearBit(fromIndex) возвращает следующий чистый индекс, начинающийся с fromIndex :
С другой стороны, previousClearBit(fromIndex) возвращает индекс ближайшего чистого индекса в противоположном направлении:
Кроме того, мы можем преобразовать BitSet в byte[] или long[] с помощью методов toByteArray () | или toLongArray () | соответственно:
5. Заключение
В этом уроке мы увидели, как мы можем использовать BitSet s для представления вектора битов.
Сначала мы познакомились с обоснованием отказа от использования boolean[] для представления вектора битов. Затем мы увидели, как BitSet работает внутри и как выглядит его API.
и скобок обнулить все младшие биты числа. Т.е., например, в результате данного преобразования, число 0b10101111 должно превратиться в 0b10000000. Число от 0 до 2^64-1.
Если такое вообще реально. Условные операторы использовать нельзя.
Upd.:Сдвиги использовать можно. Забыл сказать


без операций сдвига или умножения/деления нереально, поскольку все эти три операции побитовые - каждый бит обрабатывается независимо от других, следовательно нет возможности отличить один от другого
Почитать K&R. Задание для лабораторки наверняка по ней составляли :)

Сдвиги использовать можно?

вообще тупо long long a = 0x8000000000000000

> вообще тупо long long a = 0x8000000000000000
именно тупо, нужно использовать uint64_t, или __int64 для Wыn32

Да, чорт, забыл о том, что старший бит может быть нулевым. Вот тупняк

не совсем понятно
0b10101111 & 0b10000000 разве не подходит?

а, большое число.
для long long & нету?

Если я правильно понял ТС, то ему нужно обнулить младшие 8 бит?

нет, ему надо обнулить всё, кроме первого


>Если я правильно понял ТС, то ему нужно обнулить младшие 8 бит?
Если я правильно понял задание, то нужно для произвольной наперёд заданной разрядности сбросить все младшие биты.
Читайте также:


