Моделирование популяции животных в excel решение практическая работа 8
Попробуем при помощи электронной таблицы Excel смоделировать динамику численности двух популяций, выбрав такие значения констант:
| r1 = 0,1 | p1 = 0,001 | d2 = 0,05 | p2 = 0,00005 |
| (выбранные значения можно будет поменять, но это уже следующий уровень сложности работы). | |||
| Создайте новую книгу, в которой на первом листе будут три столбца - номер поколения, численности жертвы и хищника (см. рис. справа). Введите номер поколения (естественно, 1), а также начальную численности жертв (1000 особей) и хищников (100 особей). Чтобы не нумеровать поколения вручную (а заодно потренироваться в ведении формул в ячейки таблицы), поступим так: В ячейке А3 (под единицей) кликнем левой кнопкой мыши (активизируем ее) и введем =A2+1 и нажмем [Enter] . (т.е. в этой ячейке значение будет на единицу больше, чем в предыдущей). | 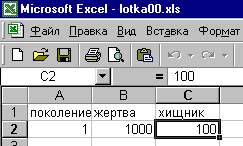 |
| Теперь к квадратику в правом нижнем углу активной ячейки ( А3 ) подведем курсор мыши, и тогда он примет вид крестика. Нажав левую кнопку мыши, растянем эту ячейку вниз на столько поколений, на сколько сочтете нужным. Теперь введем в ячейку В3 формулу Уравнения Лотка-Вольтерра для жертвы (вместо значений N1 и N2 пользуемся номерами ячеек, в которых они находятся - В2 и С2 соответственно, а цифровые значения - из таблицы выше): =0,1*B2-0,001*B2*C2+B2 и нажмем [Enter] (появление еще одного слагаемого, B2 , связано с тем, что формула показывает изменение начальной численности, т.о. чтобы получить количество особей второго поколения, необходимо прибавить к выражению численность предыдущего поколения). Теперь к квадратику в правом нижнем углу активной ячейки ( В3 ) подведем курсор мыши (он опять примет вид крестика) и, нажав левую кнопку, растянем и эту ячейку вниз на столько поколений, на сколько сочтете нужным. При этом численность жертвы начнет экспоненциально возрастать, т.к. во всех поколениях, кроме первого (по мнению программы), хищников нет. Теперь введем в ячейку С3 формулу для хищника (также вместо значений N1 и N2 пользуемся номерами ячеек В2 и С2 и цифровыми значениями из таблицы выше): =0,00005*B2*C2 - 0,05*C2+C2 и нажмем [Enter] Теперь снова растянем активную ячейку ( С3 ) на выбранное число поколений. Вы видите, что численности установятся на исходных значениях 1000 и 100 особей соответственно, т.е. популяции находятся в равновесии. Разбалансируем систему. Для этого изменим, например, численность жертвы (кликнув на ячейке В2 , введем в строке формул новое значение - например, 500 и нажмем [Enter] ). Программа сама пересчитает значения во всех ячейках, и появятся колебания численности обоих видов. | |
|
Для этого кликните мышкой по любому значению численности хищника, и в открывшемся окне ( Формат ряда данных ) выберите закладку Ось , а в ней в "Построить ряд" выберите "По вспомогательной оси" и нажмите ОК. Если было просмотрено много поколений (100-200), согласованные колебания численности будут хорошо видны на графике. Если поколений маловато, можно повторить процедуры растягивания всех трех столбцов еще на ряд поколений, активизировав по очереди нижние ячейки каждого и растягивая мышкой за правый нижний угол. В результате у автора получился такой файл с моделью динамики популяций (см. рис. слева), который можно скачать и использовать (файл lotka01.xls, 47 kb) .
Практическая работа № 6.
|
| Вложение | Размер |
|---|---|
| biologicheskie_modeli_razvitiya_populyaciy.doc | 271.5 КБ |
Предварительный просмотр:
«Биологические модели развития популяций»
Из истории вопроса
В последнее время во всём мире возрос интерес к экологическим проблемам. Экология, как наука, использует самые разнообразные методы для решения этих проблем, в том числе и математический. Историю применения математики в экологии справедливо принято исчислять с выхода в свет книги Томаса Мальтуса «Опыт о законе народонаселения» в 1798 году. В ней впервые чётко сформулировано преставление о том, что численность населения (английское слово population породило современный русский термин « популяция »), которому предоставлена возможность неограниченно размножаться, растёт во времени в геометрической прогрессии.
Следующий шаг был связан с введением модели популяции, рост численности которой не беспределен и ограничен некоторым необходимым ей ресурсом. Такая модель достаточно хорошо описывала динамику многих природных популяций и была предложена П. Ф. Ферхюльстом в 1838 году (в работе «Notice sur la lei qua la population suit dans son accroissement») и позднее получила название «логистической»:
Упомянутые выше работы были призваны описывать динамику отдельно взятой популяции, в первую очередь человеческого населения. Первые собственно математико-экологические работы, ставящие целью описание численности взаимодействующих между собой популяций, появились лишь в 20-х годах двадцатого столетия.
Самым важным результатом этих работ следует считать то, что в них было показано, как на основании биологически правдоподобных и допускающих экспериментальную проверку предположений о механизмах внутри- и межпопуляционных взаимодействий можно чисто математическими методами вывести некоторые заключения о характере динамики системы. Наиболее известным заключение такого рода явился вывод о возможности колебаний численности в системе двух популяций, взаимодействующих по принципу хищник- жертва. Этот вывод стал очевидным после того, как независимо друг от друга австрийский биофизик Альфред Лотка в своей работе «Элементы физической биологии» (1925) и итальянский математик Вито Вольтера, опубликовавший в 1926 году «Математическую теорию борьбы за существование», обосновали систему уравнений, описывающую взаимоотношения в системе хищник- жертва. В дальнейшем, Г. Ф. Гаузе была проведена экспериментальная проверка результатов, полученных А. Лотка и В. Вольтерра, которая и подтвердила правильность этих результатов.
Далее, к концу 30-х годов 20 века в развитии математической экологии наступила продолжительная пауза. Начало нового интенсивного этапа в данном направлении приходится на 60-е годы 20 века и связано с двумя обстоятельствами. Во- первых, катастрофические последствия воздействия человека на природу сделали задачу прогнозирования таких последствий весьма актуальной. Во- вторых, бурное развитие вычислительной техники и успехи её применения в решении различных задач породил естественные надежды на её применение и в экологической проблематике.
Описание модели «хищник-жертва» (модель 1)
Одним из важных этапов решения задач экологии является разработка математических моделей экологических систем.
Рассмотрим биологическое сообщество, которое состоит из нескольких популяций биологических видов, живущих в общей среде, и построим модель двувидовой борьбы в популяциях. Напомним, что широко распространённым взаимодействием между представителями различных видов является использование одними живыми организмами («хищниками») других организмов («жертв») в качестве пищи. При этом, «соперничество» жертвы с хищником выражается в изменении численности жертвы, которая в свою очередь сказывается на численности хищника.
Отметим, что дальнейшее описание взаимоотношений между двумя видами биологических популяций (жертвами и хищниками) будет основано на следующих предположениях:
- численности популяций жертв и хищников зависят только от времени и не зависят от пространственного распределения популяции на занимаемой территории;
- естественная смертность жертв не учитываются;
- скорость роста численности жертв уменьшается пропорционально численности хищников, а темп роста хищников увеличивается пропорционально численности жертв;
- эффект «насыщения» у хищника не наступает, т. е. хищник всегда голоден.
Итак, содержательная постановка задачи заключается в следующем. Пусть на одной и той же территории проживают два различных вида биологических популяций с численностями и C i , где N i - численность жертв и C i - численность хищников в момент времени i . Предположим, что единственным фактором, ограничивающим размножение жертв, является давление на них со стороны хищников, а размножение хищников ограничивается количеством добытой ими пищи (количеством жертв). Тогда, в отсутствие хищников численность жертв N i растёт с коэффициентом прироста r , т.е. N i+1 = N i +rN i , N i - количество жертв в момент времени i , r>0 . Наличие хищника, разумеется, меняет вид этого уравнения, так как если численность хищника C i , то, кроме естественного прироста, следует учесть убыль численности жертв в силу истребления жертв хищником. Эту убыль следует считать пропорциональной числу встреч между особями обоих видов, и она может быть выражена числом aN i C i , где a>0 - коэффициент пропорциональности, характеризующий вымирание жертв вследствие их встречи с хищником, N i - численность жертв в момент времени i и C i - численность хищников в момент времени i . Поэтому, считая, что численность жертв изменяется благодаря рождаемости (которая пропорциональна общей численности жертв с коэффициентом прироста равным r ) и смертности, получим:
N i+1 = N i +rN i - aN i C i
Рассуждая аналогично, имеем: численность хищников C i в отсутствие жертв убывает с некоторым естественным коэффициентом смертности q , т.е . С i+1 =С i - qC i , где C i - численность хищников в момент времени i , q>0. Численность хищников растёт тем быстрее, чем больше численность жертв. Это увеличение пропорционально числу встреч между особями обоих видов и выражается числом faN i C i , где f>0 - коэффициент пропорциональности, характеризующий потребность в пище хищника, N i - численность жертв в момент времени i и C i - численность хищников в момент времени i . Поэтому, считая, что численность хищников изменяется благодаря встречам с жертвами и скорости вымирания (которая пропорциональна общей численности хищников с коэффициентом вымирания равным q ), получим:
С i+1 =С i + faN i C i - qC i
Таким образом, взаимодействие хищника и жертвы можно описать с помощью системы уравнений:
N i+1 = N i +rN i - aN i C i
С i+1 =С i + faN i C i - qC i
Програмная реализация модели «хищник-жертва»
Данная модель была реализована на языке программирования Паскаль и в среде EXCEL. Ниже приведена программа на языке Паскаль.
Читайте также:
- Создать красивую подпись в outlook
- Сортировка по количеству символов excel
- Как сделать шеврон в фотошопе
- Как запретить ссылки в дискорд
- Режим s5 bios как включить