Место в программе где ошибка себя проявляет или становится очевидной это обнаружения
Каналы передачи данных ненадежны ( шумы , наводки и т.д.), да и само оборудование обработки информации работает со сбоями. По этой причине важную роль приобретают механизмы детектирования ошибок. Ведь если ошибка обнаружена, можно осуществить повторную передачу данных и решить проблему. Если исходный код по своей длине равен полученному коду, обнаружить ошибку передачи не предоставляется возможным. Можно, конечно, передать код дважды и сравнить, но это уже двойная избыточность .
Простейшим способом обнаружения ошибок является контроль по четности . Обычно контролируется передача блока данных ( М бит ). Этому блоку ставится в соответствие кодовое слово длиной N бит , причем N>M . Избыточность кода характеризуется величиной 1-M/N . Вероятность обнаружения ошибки определяется отношением M/N (чем меньше это отношение , тем выше вероятность обнаружения ошибки, но и выше избыточность ).
При передаче информации она кодируется таким образом, чтобы с одной стороны характеризовать ее минимальным числом символов, а с другой – минимизировать вероятность ошибки при декодировании получателем. Для выбора типа кодирования важную роль играет так называемое расстояние Хэмминга .
Пусть А и Б — две двоичные кодовые последовательности равной длины. Расстояние Хэмминга между двумя этими кодовыми последовательностями равно числу символов, которыми они отличаются. Например, расстояние Хэмминга между кодами 00111 и 10101 равно 2.
Можно показать, что для детектирования ошибок в n битах схема кодирования требует применения кодовых слов с расстоянием Хэмминга не менее N + 1 . Можно также показать, что для исправления ошибок в N битах необходима схема кодирования с расстоянием Хэмминга между кодами не менее 2N + 1 . Таким образом, конструируя код, мы пытаемся обеспечить расстояние Хэмминга между возможными кодовыми последовательностями большее, чем оно может возникнуть из-за ошибок.
Широко распространены коды с одиночным битом четности . В этих кодах к каждым М бит добавляется 1 бит , значение которого определяется четностью (или нечетностью) суммы этих М бит . Так, например, для двухбитовых кодов 00 , 01 , 10 , 11 кодами с контролем четности будут 000 , 011 , 101 и 110 . Если в процессе передачи один бит будет передан неверно, четность кода из М+1 бита изменится.
Предположим, что частота ошибок ( BER – Bit Error Rate ) равна р = 10 -4 . В этом случае вероятность передачи 8 бит с ошибкой составит 1 – (1 – p) 8 = 7,9 х 10 -4 . Добавление бита четности позволяет детектировать любую ошибку в одном из переданных битах. Здесь вероятность ошибки в одном из 9 битов равна 9p(1 – p) 8 . Вероятность же реализации необнаруженной ошибки составит 1 – (1 – p) 9 – 9p(1 – p) 8 = 3,6 x 10 -7 . Таким образом, добавление бита четности уменьшает вероятность необнаруженной ошибки почти в 1000 раз. Использование одного бита четности типично для асинхронного метода передачи. В синхронных каналах чаще используется вычисление и передача битов четности как для строк, так и для столбцов передаваемого массива данных. Такая схема позволяет не только регистрировать, но и исправлять ошибки в одном из битов переданного блока.
Контроль по четности достаточно эффективен для выявления одиночных и множественных ошибок в условиях, когда они являются независимыми. При возникновении ошибок в кластерах бит метод контроля четности неэффективен, и тогда предпочтительнее метод вычисления циклических сумм ( CRC — Cyclic Redundancy Check ). В этом методе передаваемый кадр делится на специально подобранный образующий полином . Дополнение остатка от деления и является контрольной суммой.
В Ethernet вычисление CRC производится аппаратно. На рис. 4.1 показан пример реализации аппаратного расчета CRC для образующего полинома R(x) = 1 + x 2 + x 3 + x 5 + x 7 . В этой схеме входной код приходит слева.
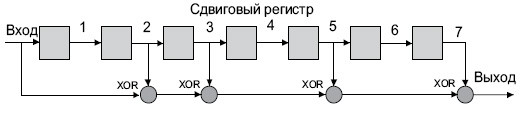
Эффективность CRC для обнаружения ошибок на многие порядки выше простого контроля четности . В настоящее время стандартизовано несколько типов образующих полиномов . Для оценочных целей можно считать, что вероятность невыявления ошибки в случае использования CRC , если ошибка на самом деле имеет место , равна (1/2) r , где r — степень образующего полинома .
4.1. Алгоритмы коррекции ошибок

Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2442 в закладки, 394k прочтений)?
Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводим, ведь мужик дело говорит.
Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»
Мы уже перевели 26 (из 30) глав. И ведем работу над изданием «в бумаге».
Глава 12. Коды с коррекцией ошибок
Заметим первым делом, что этот существенный сдвиг произошёл только потому, что я испытывал огромное эмоциональное напряжение в тот момент и это характерно для большинства великих открытий. Спокойная работа позволит вам улучшить и подробнее разработать идеи, но прорыв обычно приходит только после большого стресса и эмоциональной вовлечёности. Спокойный, холодный, не вовлечённый исследователь редко делает действительно большие новые шаги.
Вернёмся к рассказу. Я знал из предыдущих обсуждений, что конечно можно было бы соорудить три экземляра вычислителя, включая сравнивающие схемы, и использовать исправление ошибок методом голосования большинства. Но чего бы это стоило! Конечно, были и лучшие методы. Я также знал, как обсуждалось в предыдущей главе, о классной штуке с контролем чётности. Я разобрался в их строении очень внимательно.
С другой стороны, Пастер сказал: «Удача любит подготовленных». Как видите, я был подготовлен моей предыдущей работой. Я более чем хорошо знал кодирование «2-из-5», я понимал их фундаментально и работал и понимал общие последствия контроля чётности.


Перенесёмся сейчас на несколько недель позднее. Чтобы попасть в Нью-Йорк, я должен был добраться чуть раньше в Мюррей Хилл, Нью-Джерси, где я работал, и прокатиться на машине, доставляющей почту для компании. Ну да, поездка через северный Нью-Джерси ранним утром не очень живописна, поэтому я завёл привычку пересматривать свои достижения, так что перо вертелось в руках автоматически. В частности я крутил в голове прямоугольные коды. Внезапно, и я не знаю причин для этого, я обнаружил, что если я возьму треугольник и размещу биты контроля чётности на диагонали с тем, чтобы каждый бит проверял столбец и строку одновременно, то я получу более приемлемую избыточность, Рис 12.II.

Когда я возвратился к идее после нескольких дней отвлекающих событий (в конце концов, предполагалось, что я способствовал командным усилиям компании), я наконец решил, что хороший подход должен будет использовать синдром ошибки как двоичное число, указывающее место ошибки, с, конечно, всеми нулевыми битами в случае корректного результата (более лёгкий тест, чем для всех единиц на большинстве компьютеров). Заметьте, знакомство с двоичной системой, которая не была тогда распространена (1947-1948) неоднократно играло заметную роль в моих построениях. Это плата за знание большего, чем нужно сиюминутно!
Как Вы сконструируете этот частный случай кода, исправляющего ошибки? Легко! Запишите позиции в двоичном коде:

Теперь очевидно, что проверка чётности в правой половине синдрома должна включать все позиции, имеющие 1 в правом столбце; вторая цифра справа должна включить числа, имеющие 1 во втором столбце и т.д. Поэтому Вы имеете:

Таким образом, если ошибка происходит в некотором разряде, соответствующие проверки чётности (и только эти) провалятся и дадут 1 в синдроме, это составит в точности двоичное представление позиции ошибки. Это просто!




Таким образом я должен был отнестись серьёзно к тому, что я знал как абстракцию Пифагоровой функции расстояния.
Имея понятие расстояние, мы можем определить сферу как все точки (вершины, поскольку всё рассматривается в множестве вершин), на фиксированном расстоянии от центра. Например, в 3-мерном кубе, который может быть легко нарисован, Рис. 12.III, точки (0,0,1), (0,1,0), и (1,0,0) находятся на единичном расстоянии от (0,0,0), в то время как точки (1,1,0), (1,0,1), и (0,1,1) находятся на расстоянии 2 далее, и наконец точка (1,1,1) находится на расстоянии 3 от начала координат.

Таким образом построение кода с коррекцией ошибок в точности то же, что построение множества кодовых точек в n-мерном пространстве

Ранее я показал как разработать коды, удовлетворяющие условиям в случае, когда минимальное расстояние равно 1,2, 3 или 4. Коды с большими минимальными расстояниями не так легко описываются и мы не пойдем далее в этом направлении. Легко найти верхнюю оценку того, насколько велики могут быть кодовые расстояния. Очевидно, что количество точек в сфере радиуса k есть (C(n, k) — биномиальный коэффициент)

Следовательно, если мы разделим объём всего пространства, 2^n, на объём сферы, то частное будет оценкой сверху числа не пересекающихся сфер, т.е. точек кода, в соответствующем пространстве. Чтобы получить дополнительное обнаружение ошибок, мы как и прежде добавим полную проверку чётности, таким образом увеличив минимальное расстояние, которое было 2k+1, до 2k+2 (так как любые две точки на минимальном расстоянии будут иметь одинаковую чётность, увеличим минимальное расстояние на 1).
Давайте подведём итог, где мы теперь. Мы видим, что надлежащим построением кода мы можем создать систему из ненадёжных частей и получить гораздо более надёжную машину, и мы видим сколько мы должны заплатить за это оборудование, хотя мы не исследовали стоимость скорости вычисления, если мы создаём компьютер с таким уровнем коррекции ошибок. Но я ранее упомянул другую выгоду, а именно обслуживание при эксплуатации, и я хотел бы напомнить о нём снова. Чем более изощрённое оборудование, а мы очевидно движемся в этом направлении, тем более насущным является эксплуатационное обслуживание, коды с исправлением ошибок означают, что оборудование не только будет давать (возможно) верные ответы, но и может быть успешно обслужено низкоквалифицированным персоналом.
В конце лета 1961 года во время профессорского отпуска я рулил через всю страну от Стэнфорда, Калифорния к Лаборатории Белл Телефоун в Нью-Джерси. Я запланировал остановку в Моррисе, Иллинойс, где телефонная компания устанавливала первую электронную телефонную станцию, которая была уже не экспериментальной. Я знал, что станция активно использовала коды Хэмминга и, конечно, я был приглашён. Мне сказали, что никогда установка не проходила так легко, как эта. Я сказал себе: «Конечно, именно это я проповедовал в течение прошлых 10 лет». Когда во время начальной наладки все модули установлены и работают должным образом (и Вы в каком-то смысле знаете, что это из-за самопроверок и корректировки), и Вы поворачиваетесь, чтобы перейти к следующим шагам, если что-то пойдёт не так, оборудование вам просто скажет об этом! Лёгкость начальной установки, а также последующего обслуживания, просто была видна невооружённым глазом! Я могу не преувеличивать, исправление ошибок не только приводило к верным результатам во время работы, но и будучи применено правильно, значительно способствовало установке и обслуживанию на месте. И чем более изощрённо оборудование, тем более важны эти вещи!
Я хочу обратиться к другой части этой главы. Я аккуратно рассказал Вам многое из того, с чем я столкнулся на каждом этапе в обнаружении кодов с коррекцией ошибок, и что я сделал. Я сделал это по двум причинам. Во-первых, я хотел быть честным с Вами и показать Вам, как легко, следуя правилу Пастера «Удача улыбнётся подготовленным», преуспеть, просто готовя себя к успеху. Да, были элементы удачи в открытии; но в почти такой же ситуации было много других людей, и они не делали этого! Почему я? Удача, что и говорить, но также я подготовил себя к пониманию того, что происходило — больше, чем другие люди вокруг, просто реагировавшие на явления, когда они происходили, и не думающие глубоко относительно того, что было скрыто под поверхностью.
Я теперь бросаю вызов Вам. То, что я записал на нескольких страницах, было сделано в течение в общей сложности приблизительно трёх — шести месяцев, главным образом рабочих, в моменты обычного исполнения моих рабочих обязанностей в компании. (Патентование отсрочило публикацию более чем на год). Может ли кто-либо сказать, что он, на моём месте, возможно, не сделал бы это? Да, Вы так же способны, как и я, были сделать это — если бы Вы были там, и Вы подготовились также!
Конечно, проживая свою жизнь, Вы не знаете к чему готовиться — Вы хотите совершить нечто значительное и не потратить всю Вашу жизнь, являясь «швейцаром науки» или чем Вы ещё занимаетесь. Конечно, удача играет видную роль. Но насколько я вижу, жизнь дарит Вам многие, многие возможности для того, чтобы сделать нечто большое (определите это как хотите сами) и подготовленный человек обычно достигает успеха один или несколько раз, а неподготовленный человек будет проваливаться почти каждый раз.
Вышеупомянутое мнение не основано на этом опыте, или просто на моих собственных событиях, это — результат изучения жизней многих великих учёных. Я хотел быть учёным, следовательно я изучил их, и я изучил открытия, произошедшие там, где я был, я задавал вопросы тем, кто сделал это. Это мнение также основано на здравом смысле. Вы растите в себе стиль выполнения больших свершений, и затем, когда возможность находится, Вы почти автоматически реагируете с максимальной крутизной в своих действиях. Вы обучили себя думать и действовать надлежащим способам.
Существует один противный тезис, который надо упомянуть, однако, что быть великим в эпоху — это не то, что нужно в последующие годы уточнить. Таким образом Вы, готовя себя к будущим великим свершениям (а их возможность более распространена и их легче достигнуть, чем Вы думаете, так как не часто распознают большие свершения, когда это происходит под носом), необходимо думать о природе будущего, в котором Вы будете жить. Прошлое является частичным руководством, и единственное, что Вы имеете помимо истории, есть постоянное использование Вашего собственного воображения. Снова, случайный перебор случайных решений не приведёт Вас куда либо так далеко, как решения, принятые с Вашим собственным видением того, каким Ваше будущее должно быть.
Я и рассказал и показал Вам, как быть великим; теперь у Вас нет оправдания того, что Вы не делаете этого!
Продолжение следует.
Кстати, мы еще запустили перевод еще одной крутейшей книги — «The Dream Machine: История компьютерной революции»)
Ошибки в программах могут допускаться от самого начального этапа составления алгоритма решения задачи до окончательного оформления программы. Разновидностей ошибок достаточно много. Рассмотрим некоторые группы ошибок и соответствующие примеры:
Вид ошибки | Пример |
Неправильная постановка задачи | Правильное решение неверно сформулированной задачи |
Неверный алгоритм | Выбор алгоритма, который привел к неточному или неэффективному решению задачи |
Ошибка анализа | Неполный перечень ситуаций, которые могут возникнуть при решении задачи, наличие логических ошибок |
Семантические ошибки | Неправильное понимание порядка выполнение оператора |
Синтаксические ошибки | Нарушение правил, которые определяются выбранным ЯП |
Ошибки при выполнении операций | Использование слишком большого числа, деление на ноль, извлечение квадратного корня из отрицательного не комплексного числа и т.д. |
Ошибки в данных | Неправильно определен возможный диапазон изменения данных |
Опечатки | Неправильное использование схожих по внешнему виду символов |
Ошибки ввода/вывода | Неправильное считывание входных данных, неправильное задание форматов данных |
ошибки обращения к данным,
ошибки описания данных,
ошибки вычислений,
ошибки при сравнении,
ошибки в передаче управления,
ошибки ввода-вывода,
ошибки интерфейса,

В теории информации и теории кодирования с приложениями в информатике и связи , обнаружения и коррекции ошибок или защиты от ошибок методы , которые дают возможность надежной доставки из цифровых данных по ненадежным каналам связи . Многие каналы связи подвержены канальному шуму , поэтому при передаче от источника к приемнику могут возникать ошибки. Методы обнаружения ошибок позволяют обнаруживать такие ошибки, а исправление ошибок во многих случаях позволяет восстановить исходные данные.
СОДЕРЖАНИЕ
Определения
Обнаружение ошибок - это обнаружение ошибок, вызванных шумом или другими помехами во время передачи от передатчика к приемнику.
Исправление ошибок - это обнаружение ошибок и восстановление исходных безошибочных данных.
История
В классической древности, переписчики о еврейской Библии были выплачены за их работу в соответствии с количеством stichs (стихотворных строк). Поскольку прозаические книги Библии почти никогда не писались стихами, переписчикам, чтобы оценить объем работы, приходилось пересчитывать буквы. Это также помогло обеспечить точность передачи текста при изготовлении последующих копий. Между 7-м и 10-м веками н.э. группа еврейских писцов формализовала и расширила это, чтобы создать Масору с цифрами, чтобы обеспечить точное воспроизведение священного текста. Он включал подсчет количества слов в строке, разделе, книге и группах книг, отмечая средний стежок книги, статистику использования слов и комментарии. Стандарты стали такими, что отклонение даже в одной букве в свитке Торы считалось недопустимым. Эффективность их метода исправления ошибок была подтверждена точностью копирования на протяжении веков, продемонстрированной открытием свитков Мертвого моря в 1947-1956 годах, датируемых примерно 150 г. до н.э. - 75 г. н.э.
Современная разработка кодов исправления ошибок приписывается Ричарду Хэммингу в 1947 году. Описание кода Хэмминга появилось в « Математической теории коммуникации» Клода Шеннона и было быстро обобщено Марселем Дж . Э. Голеем .
Вступление
Хорошая эффективность контроля ошибок требует, чтобы схема выбиралась на основе характеристик канала связи. Общие модели каналов включают модели без памяти, в которых ошибки возникают случайным образом и с определенной вероятностью, и динамические модели, в которых ошибки возникают в основном пакетами . Следовательно, ошибки обнаружения и исправления коды могут быть в общем различие между случайным-обнаружения ошибок / коррекции и пакеты ошибок обнаружения / коррекции . Некоторые коды могут также подходить для сочетания случайных ошибок и пакетных ошибок.
Если характеристики канала не могут быть определены или сильно изменяются, схема обнаружения ошибок может быть объединена с системой для повторных передач ошибочных данных. Это называется автоматическим запросом на повторение (ARQ) и чаще всего используется в Интернете. Альтернативный подход к контролю ошибок - это гибридный автоматический запрос на повторение (HARQ), который представляет собой комбинацию ARQ и кодирования с исправлением ошибок.
Виды исправления ошибок
Есть три основных типа исправления ошибок.
Автоматический повторный запрос (ARQ)
Обычно, когда передатчик не получает подтверждения до истечения тайм-аута (т. Е. В течение разумного промежутка времени после отправки кадра данных), он повторно передает кадр до тех пор, пока он не будет либо правильно принят, либо ошибка не сохранится сверх заранее определенного количества повторных передач. .
ARQ подходит, если канал связи имеет переменную или неизвестную пропускную способность , например, в случае с Интернетом. Однако ARQ требует наличия обратного канала , что приводит к возможному увеличению задержки из-за повторных передач и требует обслуживания буферов и таймеров для повторных передач, что в случае перегрузки сети может создать нагрузку на сервер и общую пропускную способность сети.
Например, ARQ используется на коротковолновых линиях радиосвязи в форме ARQ-E или в сочетании с мультиплексированием как ARQ-M .
Прямое исправление ошибок
Коды с исправлением ошибок обычно различают сверточные коды и блочные коды :
- Сверточные коды обрабатываются побитно. Они особенно подходят для аппаратной реализации, а декодер Витерби обеспечивает оптимальное декодирование .
- Блочные коды обрабатываются поблочно . Ранние примеры блочных кодов кода повторения , коды Хэмминга и многомерные проверочные коды . За ними последовал ряд эффективных кодов, наиболее заметными из которых стали коды Рида – Соломона из-за их широкого распространения в настоящее время. Турбокоды и коды с низкой плотностью проверки четности (LDPC) - это относительно новые конструкции, которые могут обеспечить почти оптимальную эффективность .
Теорема Шеннона является важной теоремой прямого исправления ошибок и описывает максимальную скорость передачи информации, при которой возможна надежная связь по каналу с определенной вероятностью ошибки или отношением сигнал / шум (SNR). Этот строгий верхний предел выражается в пропускной способности канала . Более конкретно, в теореме говорится, что существуют коды, такие, что с увеличением длины кодирования вероятность ошибки на дискретном канале без памяти может быть сколь угодно малой при условии, что скорость кода меньше, чем пропускная способность канала. Скорость коды определяются как дробь к / п из к исходным символам и п кодированных символов.
Фактическая максимальная разрешенная кодовая скорость зависит от используемого кода исправления ошибок и может быть ниже. Это связано с тем, что доказательство Шеннона носило только экзистенциальный характер и не показало, как создавать коды, которые одновременно являются оптимальными и имеют эффективные алгоритмы кодирования и декодирования.
Гибридные схемы
Гибридный ARQ - это комбинация ARQ и прямого исправления ошибок. Есть два основных подхода:
Последний подход особенно привлекателен для канала стирания при использовании бесскоростного кода стирания .
Схемы обнаружения ошибок
Существует огромное количество различных конструкций хеш-функций. Однако некоторые из них имеют особенно широкое распространение из-за их простоты или их пригодности для обнаружения определенных видов ошибок (например, производительности циклического контроля избыточности при обнаружении пакетных ошибок ).
Кодирование минимального расстояния
Код с исправлением случайных ошибок, основанный на кодировании с минимальным расстоянием, может обеспечить строгую гарантию количества обнаруживаемых ошибок, но не может защитить от атаки по прообразу .
Коды повторения
Код повторения очень неэффективен и может быть подвержен проблемам, если ошибка возникает точно в одном и том же месте для каждой группы (например, «1010 1010 1010» в предыдущем примере будет обнаружено как правильное). Преимущество кодов повторения состоит в том, что они чрезвычайно просты и фактически используются в некоторых передачах цифровых станций .
Бит четности
Бит четности является бит , который добавляется к группе исходных битов , чтобы гарантировать , что количество установленных битов (то есть, биты со значением 1) в исходе четным или нечетным. Это очень простая схема, которую можно использовать для обнаружения одиночного или любого другого нечетного числа (т. Е. Трех, пяти и т. Д.) Ошибок в выходных данных. Четное количество перевернутых битов сделает бит четности правильным, даже если данные ошибочны.
Существуют также другие методы группировки битов.
Контрольная сумма
Схемы контрольных сумм включают биты четности, контрольные цифры и проверки с продольным избыточным кодом . Некоторые схемы контрольных сумм, такие как Даммы алгоритм , в алгоритме Лун , и алгоритм верхуфф , специально предназначены для обнаружения ошибок , обычно вносимых человеком в написании или запоминании идентификационных номеров.
Циклическая проверка избыточности
Циклический избыточный код (CRC) представляет собой незащищенное хэш - функция предназначена для обнаружения случайных изменений цифровых данных в компьютерных сетях. Он не подходит для обнаружения злонамеренно внесенных ошибок. Он характеризуется указанием порождающего полинома , который используется в качестве делителя в полиномиальном длинном делении над конечным полем , принимая входные данные в качестве делимого . Остальное становится результатом.
У CRC есть свойства, которые делают его хорошо подходящим для обнаружения пакетных ошибок . CRC особенно легко реализовать на оборудовании и поэтому обычно используются в компьютерных сетях и устройствах хранения, таких как жесткие диски .
Бит четности можно рассматривать как 1-битную CRC особого случая.
Криптографическая хеш-функция
Код исправления ошибок
Для обнаружения ошибок можно использовать любой код исправления ошибок. Код с минимальным расстоянием Хэмминга , d , может обнаруживать до d - 1 ошибок в кодовом слове. Использование кодов с коррекцией ошибок на основе минимального расстояния для обнаружения ошибок может быть подходящим, если требуется строгое ограничение на минимальное количество обнаруживаемых ошибок.
Коды с минимальным расстоянием Хэмминга d = 2 являются вырожденными случаями кодов с исправлением ошибок и могут использоваться для обнаружения одиночных ошибок. Бит четности является примером кода обнаружения одиночной ошибки.
Приложения
Приложения, которым требуется низкая задержка (например, телефонные разговоры), не могут использовать автоматический запрос на повторение (ARQ); они должны использовать прямое исправление ошибок (FEC). К тому времени, когда система ARQ обнаружит ошибку и повторно передаст ее, повторно отправленные данные прибудут слишком поздно, чтобы их можно было использовать.
Приложения, в которых передатчик сразу же забывает информацию, как только она отправляется (например, большинство телекамер), не могут использовать ARQ; они должны использовать FEC, потому что при возникновении ошибки исходные данные больше не доступны.
Приложения, использующие ARQ, должны иметь обратный канал ; приложения, не имеющие обратного канала, не могут использовать ARQ.
Приложения, требующие крайне низкого уровня ошибок (например, цифровые денежные переводы), должны использовать ARQ из-за возможности неисправимых ошибок с помощью FEC.
Техника обеспечения надежности и контроля также использует теорию кодов с исправлением ошибок.
Интернет
В типичном стеке TCP / IP контроль ошибок выполняется на нескольких уровнях:
- Каждый кадр Ethernet использует обнаружение ошибок CRC-32 . Кадры с обнаруженными ошибками отбрасываются аппаратурой приемника.
- IPv4 - заголовок содержит контрольную сумму , защищающее содержимое заголовка. Пакеты с неверными контрольными суммами отбрасываются в сети или на приемнике.
- Контрольная сумма была опущена в заголовке IPv6 , чтобы минимизировать затраты на обработку при сетевой маршрутизации и поскольку предполагается, что текущая технология канального уровня обеспечивает достаточное обнаружение ошибок (см. Также RFC 3819).
- UDP имеет необязательную контрольную сумму, покрывающую полезную нагрузку и адресную информацию в заголовках UDP и IP. Пакеты с неверными контрольными суммами отбрасываются сетевым стеком . Контрольная сумма не является обязательной для IPv4 и требуется для IPv6. Если не указано иное, предполагается, что уровень канала передачи данных обеспечивает желаемый уровень защиты от ошибок.
- TCP предоставляет контрольную сумму для защиты полезной нагрузки и адресной информации в заголовках TCP и IP. Пакеты с неверными контрольными суммами отбрасываются сетевым стеком и в конечном итоге повторно передаются с использованием ARQ либо явно (например, посредством трехстороннего рукопожатия ), либо неявно из-за тайм-аута .
Телекоммуникации в дальнем космосе
Разработка кодов исправления ошибок была тесно связана с историей полетов в дальний космос из-за чрезмерного ослабления мощности сигнала на межпланетных расстояниях и ограниченной доступной мощности на борту космических зондов. В то время как ранние миссии отправляли свои данные в незашифрованном виде, начиная с 1968 года, цифровая коррекция ошибок была реализована в форме (субоптимально декодированных) сверточных кодов и кодов Рида-Мюллера . Код Рида-Мюллера хорошо подходил к шуму, которому подвергался космический корабль (приблизительно соответствуя колоколообразной кривой ), и был реализован для космического корабля Mariner и использовался в миссиях между 1969 и 1977 годами.
В Voyager 1 и Voyager 2 миссии, которая началась в 1977 году, были разработаны , чтобы обеспечить цветное изображение и научную информацию от Юпитера и Сатурна . Это привело к повышенным требованиям к кодированию, и, таким образом, космический аппарат поддерживался (оптимально декодированным по Витерби ) сверточными кодами, которые можно было объединить с внешним кодом Голея (24,12,8) . Корабль "Вояджер-2" дополнительно поддерживал реализацию кода Рида-Соломона . Конкатенированный код Рида – Соломона – Витерби (RSV) позволил произвести очень мощную коррекцию ошибок и позволил космическому кораблю совершить длительное путешествие к Урану и Нептуну . После модернизации системы ECC в 1989 году оба корабля использовали кодирование V2 RSV.
Консультативный комитет по системам космических данных в настоящее время рекомендует использование кодов коррекции ошибок с производительностью аналогична кодой RSV Voyager 2 как минимум. Составные коды все больше теряют популярность в космических полетах и заменяются более мощными кодами, такими как турбокоды или коды LDPC .
Различные виды выполняемых миссий в дальний космос и орбитальные полеты предполагают, что попытка найти универсальную систему исправления ошибок будет постоянной проблемой. Для миссий, близких к Земле, характер шума в канале связи отличается от того, который испытывает космический корабль во время межпланетной миссии. Кроме того, по мере того, как космический корабль удаляется от Земли, проблема коррекции шума становится все более сложной.
Спутниковое вещание
Спрос на пропускную способность спутникового ретранслятора продолжает расти, чему способствует желание предоставлять телевидение (включая новые каналы и телевидение высокой четкости ) и данные IP. Доступность транспондеров и ограничения полосы пропускания ограничили этот рост. Пропускная способность транспондера определяется выбранной схемой модуляции и долей пропускной способности, потребляемой FEC.
Хранилище данных
Коды обнаружения и исправления ошибок часто используются для повышения надежности носителей данных. Дорожка четности, способная обнаруживать однобитовые ошибки, присутствовала в первом хранилище данных на магнитной ленте в 1951 году. Оптимальный прямоугольный код, используемый в записывающих лентах с групповым кодированием, не только обнаруживает, но и исправляет однобитовые ошибки. Некоторые форматы файлов , особенно форматы архивов , включают контрольную сумму (чаще всего CRC32 ) для обнаружения повреждения и усечения и могут использовать файлы избыточности или четности для восстановления частей поврежденных данных. Коды Рида-Соломона используются в компакт-дисках для исправления ошибок, вызванных царапинами.
Современные жесткие диски используют коды Рида – Соломона для обнаружения исправления незначительных ошибок при чтении секторов, а также для восстановления поврежденных данных из неисправных секторов и сохранения этих данных в резервных секторах. В системах RAID используются различные методы исправления ошибок для восстановления данных, когда жесткий диск полностью выходит из строя. Файловые системы, такие как ZFS или Btrfs , а также некоторые реализации RAID поддерживают очистку данных и повторное обновление, что позволяет обнаруживать и (надеюсь) восстанавливать плохие блоки перед их использованием. Восстановленные данные могут быть перезаписаны точно в том же физическом месте, чтобы освободить блоки в другом месте на том же оборудовании, или данные могут быть перезаписаны на заменяющее оборудование.
Память с исправлением ошибок
Динамическая память с произвольным доступом (DRAM) может обеспечить более надежную защиту от мягких ошибок , полагаясь на коды исправления ошибок. Такая память с коррекцией ошибок, известная как память с защитой ECC или EDAC , особенно желательна для критически важных приложений, таких как научные вычисления, финансы, медицина и т. Д., А также для внеземных приложений из-за повышенной радиации в космосе.
Контроллеры памяти с исправлением ошибок традиционно используют коды Хэмминга , хотя некоторые используют тройное модульное резервирование . Чередование позволяет распределить эффект одного космического луча, потенциально нарушающего несколько физически соседних битов по нескольким словам, путем связывания соседних битов с разными словами. До тех пор, пока нарушение единичного события (SEU) не превышает пороговое значение ошибки (например, одиночная ошибка) в любом конкретном слове между доступами, оно может быть исправлено (например, с помощью однобитового кода исправления ошибок), и иллюзия безошибочной системы памяти может сохраняться.
В дополнение к аппаратным средствам, обеспечивающим функции, необходимые для работы памяти ECC, операционные системы обычно содержат соответствующие средства отчетности, которые используются для предоставления уведомлений при прозрачном восстановлении программных ошибок. Одним из примеров является Linux ядро «s EDAC подсистема (ранее известный как Bluesmoke ), который собирает данные от ошибок проверки с поддержкой компонентов внутри компьютерной системы; Помимо сбора и отправки отчетов о событиях, связанных с памятью ECC, он также поддерживает другие ошибки контрольной суммы, в том числе обнаруженные на шине PCI . Некоторые системы также поддерживают очистку памяти для выявления и исправления ошибок на раннем этапе, прежде чем они станут неисправимыми.
Читайте также:


