Линия тренда в excel как построить

Обновлено: 07.01.2025

Очень часто на графиках с большим количеством информации содержит колебания (шумы), из-за которых усложняется восприятия информации. Благодаря линиям тренду можно экспонировать главную тенденцию, которую отображает график. Линия тренда как будто визуально отфильтровывает шумы на графике, а информация становится более понятной.

Как добавить линию тренда на график

Данные в диапазоне A1:B7 отобразим на графике и найдем линейную функциональную зависимость y=f(x):

1. Выделите диапазон A1:B7 и выберите инструмент: «Вставка»-«Диаграммы»-«Точечная»-«Точечная с гладкими кривыми и маркерами».
2. Когда график активный нам доступная дополнительная панель, а в ней выберите инструмент: «Работа с диаграммами»-«Макет»-«Линия тренда»-«Линейное приближение»
3. Сделайте двойной щелчок по лини тренду и в появившемся окне поставьте галочку напротив опции: «показывать уравнение на диаграмме».

Примечание. Если на графике находится несколько линий данных, тогда предварительно следует выделить линию того графика для которого следует включить линию тренда.

Прогнозирование в Excel с помощью линии тренда

Сменим график на гистограмму, чтобы сравнить их уравнения:

1. Щелкните правой кнопкой по графику и выберите опцию из контекстного меню: «Изменить тип диаграммы».
2. В появившемся окне выберите параметр: «Гистограмма»-«Гистограмма с группировкой».

Как видно оба графика отображают одни и те же данные, но у них разные уравнения трендовых линий, сохраняется только направление тенденции (снизу вверх).

Из этого следует, что линия тренда это только аппроксимирующий (приближенный) инструмент.

Сравним уравнения на разных типах графиков. На оси координат XY:

• прямая с уравнением: y=2,4229x-3,519 пересекает вертикальную ось Y в отрицательном значении оси: y=-3,519.
• прямая с уравнением: y=2,4229x+18,287 пересекает вертикальную ось Y на уровне: y=18,287.

Чтобы визуально убедится в этом, сделаем следующее:

1. Снова измените гистограмму на точечную диаграмму. Правой кнопкой по гистограмме «Изменить тип диаграммы», далее «Точечная»-«Точечная с гладкими кривыми и маркерами».
2. Сделайте двойной щелчок по линии тренда и измените ее параметры так: «Прогноз»-«назад на:» установите значение 12,0. И нажмите ОК.

Теперь, даже визуально видно, что угол наклонения линии на разных типов графиков отличается. Но направление тенденции сохраняется. Это удобный инструмент для визуального восприятия тенденции. Но при анализе графиков его следует воспринимать как аппроксимирующий вспомогательный инструмент.

В этой теме описывается, какие параметры линии тренда доступны в Office.

Используйте линию тренда этого типа для создания прямой линии, которая наилучшим образом описывает простой линейный набор данных. Она применяется в случаях, когда точки данных расположены близко к прямой. Иначе говоря, прямая линия тренда хорошо подходит для величины, которая возрастает или убывает с постоянной скоростью.

Для расчета точек методом наименьших квадратов прямая линия тренда использует следующее уравнение:

где m — это наклон, а b — смещение.

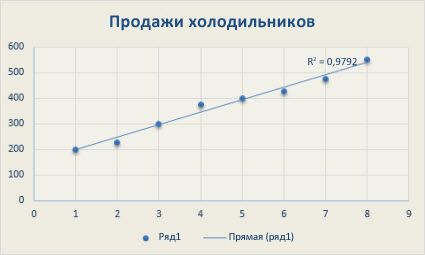
Следующая прямая линия тренда отображает стабильный рост продаж холодильников на протяжении 8 лет. Обратите внимание, что величина достоверности аппроксимации (число от 0 до 1, отображающее степень соответствия ожидаемых значений для линии тренда фактическим данным) равна 0,9792, что свидетельствует о хорошем совпадении расчетной линии с данными.

Отображая оптимизированную кривую, эта линия тренда полезна для описания величины, которая вначале быстро растет или убывает, а затем постепенно стабилизируется. Логарифмическая линия тренда может использовать отрицательные и положительные значения данных.

Для расчета точек методом наименьших квадратов логарифмическая линия тренда использует следующее уравнение:

где c и b — константы и ln — функция натурального логарифма.

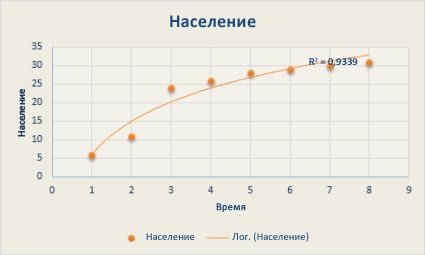
Следующая логарифмическая линия тренда отображает прогнозируемый рост численности населения животных в области с фиксированным пространством, где численность населения была выровнена в результате уменьшения пространства для животных. Обратите внимание, что величина квадрата составляет 0,933, что относительно хорошо подходит для данных.

Эта линия тренда полезна для описания величин, попеременно возрастающих и убывающих. Например, при анализе большого набора данных о нестабильной величине. Степень полинома определяется количеством экстремумов (максимумов и минимумов) кривой. Обычно полином второй степени имеет только один экстремум, полином третьей степени — один или два экстремума, а полином четвертой степени — до трех экстремумов.

Для расчета точек методом наименьших квадратов полиномиальная (или криволинейная) линия тренда использует следующее уравнение:

где b и являются константами.

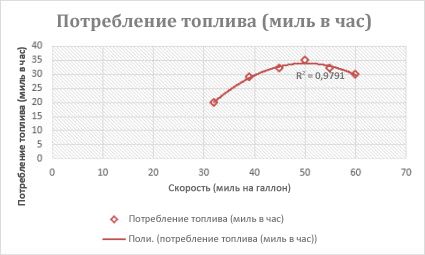
Приведенная ниже полиномиальная линия тренда второй степени (один максимум) отображает зависимость расхода топлива от скорости движения. Близкая к единице величина достоверности аппроксимации (0,979) свидетельствует о хорошем совпадении кривой с данными.

Отображая кривую, эта линия тренда полезна для отображения зависимости, которая содержится в данных, и характеризуется постоянной скоростью роста. Примером такой зависимости может служить ускорение гоночного автомобиля за каждый интервал времени, равный одной секунде. Если в данных имеются нулевые или отрицательные значения, использование степенной линии тренда невозможно.

Для расчета точек методом наименьших квадратов степенная линия тренда использует следующее уравнение:

где c и b — константы.

Примечание: При наличии нулевых или отрицательных значений данных этот параметр недоступен.

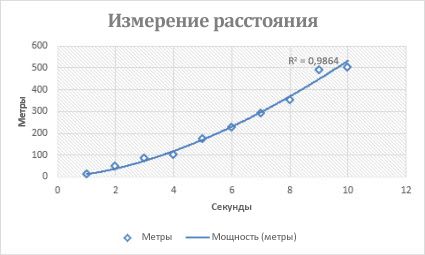
Приведенная ниже диаграмма измерения расстояний отображает зависимость пройденного расстояния от времени. Расстояние выражено в метрах, время — в секундах. Эти данные точно описываются степенной линией тренда, о чем свидетельствует величина достоверности аппроксимации, равная 0,986.

Отображая кривую, эта линия тренда полезна, если скорость изменения данных непрерывно возрастает. Однако для данных, которые содержат нулевые или отрицательные значения, экспоненциальная линия тренда неприменима.

Для расчета точек методом наименьших квадратов экспоненциальная линия тренда использует следующее уравнение:

где c и b — константы и e — основание натурального логарифма.

Приведенная ниже экспоненциальная линия тренда отображает содержание радиоактивного углерода-14 в зависимости от возраста органического объекта. Величина достоверности аппроксимации равна 0,990, что означает очень хорошее соответствие кривой данным.

Эта линия тренда позволяет сгладить колебания данных и таким образом более наглядно отображает характер зависимости. Линейный фильтр строится по определенному числу точек данных (задается параметром Точки). Элементы данных усредняются, и полученный результат используется в качестве точки линии тренда. Так, если параметр Точки равен 2, первая точка линии тренда с линейной фильтрацией определяется как среднее значение первых двух элементов данных, вторая точка — как среднее второго и третьего элементов, и так далее.

Линия тренда с линейной фильтрацией использует такое уравнение:

Число точек в линии тренда с скользящее среднее равно общему числу точек ряда за вычетом числа, указанного для параметра "Точки".

В точечной диаграмме линия тренда базируется на порядке расположения значений X в диаграмме. Для получения оптимального результата перед добавлением линейной фильтрации отсортируйте значения X.

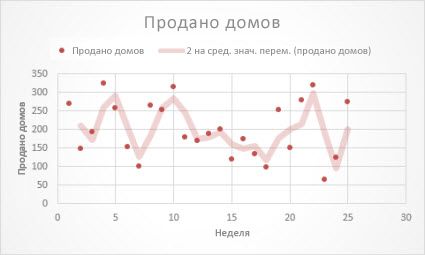
Приведенная ниже линия тренда с линейной фильтрацией отображает тенденцию числа продаж домов на протяжении 26 недель.

Важно: Начиная с Excel 2005 г., Excel скорректировал способ вычисления значения R2 для линейных линий тренда на диаграммах, где для перехватить линию тренда установлено значение 0 (0). Эта корректировка исправлять вычисления, которые дают неправильные значения R 2, и выравнивает вычисление R 2 с функцией LINEST. В результате на диаграммах, созданных в предыдущих версиях Excel, могут отображаться разные значения R2. Дополнительные сведения см. в таблице Изменения внутренних вычислений линейных линий тренда на диаграмме.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Одной из важных составляющих любого анализа является определение основной тенденции событий. Имея эти данные можно составить прогноз дальнейшего развития ситуации. Особенно наглядно это видно на примере линии тренда на графике. Давайте выясним, как в программе Microsoft Excel её можно построить.

Линия тренда в Excel

Приложение Эксель предоставляет возможность построение линии тренда при помощи графика. При этом, исходные данные для его формирования берутся из заранее подготовленной таблицы.

Построение графика

Для того, чтобы построить график, нужно иметь готовую таблицу, на основании которой он будет формироваться. В качестве примера возьмем данные о стоимости доллара в рублях за определенный период времени.

1. Строим таблицу, где в одном столбике будут располагаться временные отрезки (в нашем случае даты), а в другом – величина, динамика которой будет отображаться в графике.

Создание линии тренда

Теперь нужно непосредственно добавить линию тренда.

Находясь во вкладке «Макет» кликаем по кнопке «Линия тренда», которая расположена в блоке инструментов «Анализ». Из открывшегося списка выбираем пункт «Экспоненциальное приближение» или «Линейное приближение».

Настройка линии тренда

Имеется возможность дополнительной настройки линии.

Последовательно переходим во вкладке «Макет» по пунктам меню «Анализ», «Линия тренда» и «Дополнительные параметры линии тренда…».

• Полиномиальная;
• Линейная;
• Степенная;
• Логарифмическая;
• Экспоненциальная;
• Линейная фильтрация.

Для того, чтобы определить достоверность нашей модели, устанавливаем галочку около пункта «Поместить на диаграмму величину достоверности аппроксимации». Чтобы посмотреть результат, жмем на кнопку «Закрыть».

Если вас не удовлетворяет уровень достоверности, то можете вернуться опять в параметры и сменить тип сглаживания и аппроксимации. Затем, сформировать коэффициент заново.

Прогнозирование

Главной задачей линии тренда является возможность составить по ней прогноз дальнейшего развития событий.

Опять переходим в параметры. В блоке настроек «Прогноз» в соответствующих полях указываем насколько периодов вперед или назад нужно продолжить линию тренда для прогнозирования. Жмем на кнопку «Закрыть».

Как видим, в Эксель не составляет труда построить линию тренда. Программа предоставляет инструменты, чтобы её можно было настроить для максимально корректного отображения показателей. На основании графика можно сделать прогноз на конкретный временной период.

Мы рады, что смогли помочь Вам в решении проблемы.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.

Процедура прогнозирования

Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.

Способ 1: линия тренда

Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.

Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.

Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.

• Линейная;
• Логарифмическая;
• Экспоненциальная;
• Степенная;
• Полиномиальная;
• Линейная фильтрация.

Давайте для начала выберем линейную аппроксимацию.

Способ 2: оператор ПРЕДСКАЗ

Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:

«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.

Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.

При вычислении данным способом используется метод линейной регрессии.

Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.

Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».

В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.

Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.

Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.

Способ 3: оператор ТЕНДЕНЦИЯ

Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:

=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])

Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.

Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.

Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.

Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».

Способ 4: оператор РОСТ

Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:

=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])

Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.

Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».

Способ 5: оператор ЛИНЕЙН

Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:

=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])

Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.

Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».

Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.

Способ 6: оператор ЛГРФПРИБЛ

Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:

= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])

Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.

В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».

Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.

Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.

Мы рады, что смогли помочь Вам в решении проблемы.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Читайте также:

  
• Прошить планшет asus p001
  
• Белый экран вместо сайта во всех браузерах
  
• Как удалить прошивку с модема билайн
  
• Обновить биос на irbis
  
• Почему в браузере открываются сразу две одинаковые страницы