Лабораторная работа 1 решение задач линейного программирования с использованием microsoft excel
ЛАБОРАТОРНАЯ РАБОТА №1 «РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ Microsoft Excel 2007»
ЦЕЛЬ РАБОТЫ
Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Для модели ЛП, соответствующей номеру вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ Microsoft Excel ДЛЯ РЕШЕНИЯ ЗАДАЧ ЛП
Поиск решения – это надстройка Excel, которая позволяет решать оптимизационные задачи. Если в меню Данные отсутствует команда Поиск решения, значит, необходимо загрузить эту надстройку. Выберите кнопку “ Office ” Þ Параметры Excel Þ Надстройки и активизируйте надстройку Поиск решения.
Для того чтобы решить задачу ЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.
1. Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
- целевой функции (ЦФ),
b) ввести исходные данные в экранную форму:
- коэффициенты при переменных в ограничениях,
- правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
- формулу для расчета ЦФ,
- формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне Поиск решения):
- направление оптимизации ЦФ;
e) ввести изменяемые ячейки и ограничения (в окне Поиск решения):
- ячейки со значениями переменных,
- соотношения между правыми и левыми частями ограничений;
f) ввести параметры для решения задачи (в окне Поиск решения):
- линейная модель (для применения симплекс-метода),
- неотрицательные значения переменных.
2. Решить задачу:
a) запустить задачу на решение (в окне Поиск решения);
b) выбрать формат вывода решения (в окне Результаты поиска решения).
Одноиндексные задачи ЛП
Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:
Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис.1.1.
В экранной форме каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП. Так, например, переменным задачи (1.1) соответствуют ячейки B3 (х1), C3 (х2), коэффициентам ЦФ соответствуют ячейки B4 (с1=4), C4 (с2=16), правым частям ограничений соответствуют ячейки F 7 (b1=3), F 8 (b2=4), F 9 (b3=5) и т. д.
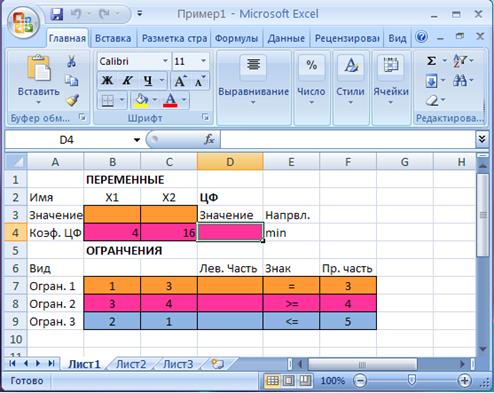
Рис.1.1. Экранная форма задачи (1.1) (курсор в ячейке D4)
Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ
В ячейку D 4, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением
Используя обозначения соответствующих ячеек в Excel (см. рис.1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B 3, C 3), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B 4, C 4), то есть
Чтобы задать формулу (1.3) необходимо в ячейку D 4 ввести следующее выражение и нажать клавишу Enter
| =СУММПРОИЗВ($ B $3:$ C $3; B 4: C 4), | (1.4) |
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится, а символ $ перед названием столбца B означает, что при копировании этой формулы в другие места листа Excel номер столбца B не изменится;
символ: означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия. После этого в целевой ячейке появится 0 (нулевое значение) (рис.1.2).
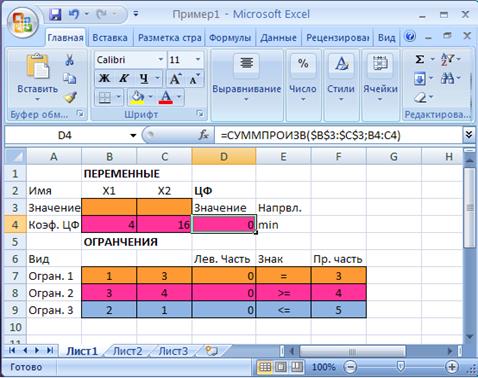
Рис.1.2. Экранная форма задачи (1.1) после ввода всех необходимых формул
(курсор в ячейке D4)
Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима Вставка функций, который можно вызвать из меню Вставка или при нажатии кнопки на стандартной панели инструментов. Так, например, формулу (1.4) можно задать следующим образом:
- курсор в поле D 4;
- нажав кнопку , вызовите окно Мастер функций – шаг 1 из 2;
- выберите в окне Категория категорию Математические;
- в окне Функция выберите функцию СУММПРОИЗВ;
- в появившемся окне СУММПРОИЗВ в строку Массив 1 введите выражение $ B $3:$ C $3, а в строку Массив 2 – выражение B 4: C 4 (рис.1.3);
- после ввода ячеек в строки Массив 1 и Массив 2 в окне СУММПРОИЗВ появятся числовые значения введенных массивов (см. рис.1.3), а в экранной форме в ячейке D 4 появится текущее значение, вычисленное по введенной формуле, то есть 0, так как в момент ввода формулы значения переменных задачи нулевые.
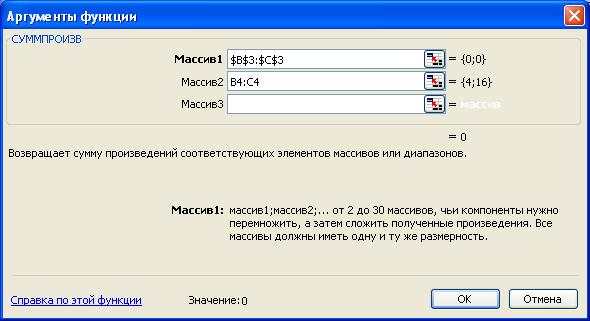
Рис.1.3. Ввод формулы для расчета ЦФ в окно СУММПРОИЗВ
Зависимости для левых частей ограничений
Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B 3, C 3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B 7, C 7 – 1-е ограничение; B 8, C 8 – 2-е ограничение и B 9, C 9 – 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл.1.1.
Решение задачи
Запуск задачи на решение
Запуск задачи на решение производится из окна Поиск решения путем нажатия кнопки Выполнить.
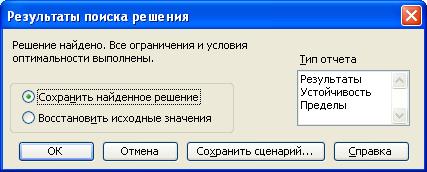
В окне Результаты поиска решения представлены названия трех типов отчетов: Результаты, Устойчивость, Пределы. Они необходимы при анализе полученного решения на чувствительность. Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку OK . После этого в экранной форме появляется оптимальное решение задачи (рис.1.10).
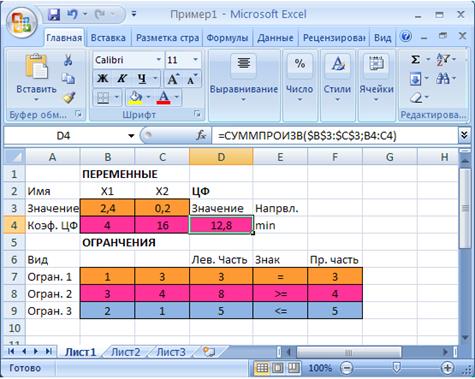
Рис.1.10. Экранная форма задачи (1.1) после получения решения
ЦЕЛЬ РАБОТЫ
Приобретение навыков построения математических моделей стандартных транспортных задач линейного программирования (ЛП) и решения их в Microsoft Excel.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Для транспортной модели ЛП, соответствующей номеру вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Ввод исходных данных
В конкретном примере осуществляется ввод мощностей четырех поставщиков (ячейки А10:А13), потребности регионов в их продукции (В9:Е9), а также удельные затраты по доставке груза от конкретного поставщика потребителю (блок В10:Е13) (рис. 2.1).
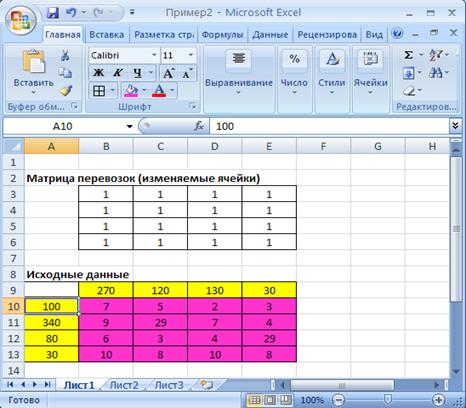
Рис.2.1. Экранная форма задачи (2.1)
Ввод граничных условий
Ввод условий реализации мощностей поставщиков
Необходимо выполнить следующие действия:
- поместить курсор в ячейку A3;
- выбрать знак S;
- выделить необходимые для суммирования ячейки ВЗ:ЕЗ;
- нажать Enter для подтверждения ввода формулы для суммирования (см.рис.2.2).
Аналогичные действия выполнить для ячеек А4, А5, А6, т. е. ввести условия реализации мощностей всех поставщиков (для всех строк).
Эти действия можно реализовать иначе:
- поместить курсор в ячейку A3;
- выбрать команду Копировать, т. е. скопировать в буфер формулу, введенную для ячейки A3;
- выделить ячейки А4:А6;
- выбрать команду Вставить, тем самым из буфера будет вставлена формула для суммирования в А4:А6.
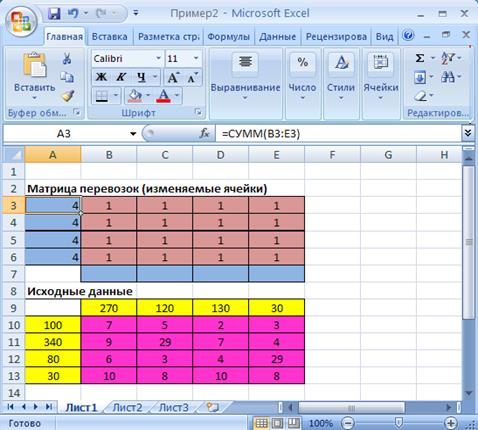
Рис.2.2. Экранная форма задачи (2.1) после суммирования ячеек B 3: E 3 (курсор в ячейке A 3)
Ввод условий удовлетворения запросов потребителей
Для этого необходимо выполнить следующие действия:
- поместить курсор в ячейку В7;
- выбрать знак S, при этом автоматически выделяется весь столбец B 3: B 6;
- нажать Enter для подтверждения суммирования показателей выделенного столбца (см.рис.2.3).
Эту же последовательность действий выполнить для ячеек С7 и Е7 или проделать следующее:
- поместить курсор в ячейку С7;
- выбрать команду Копировать;
- выделить ячейки С7:Е7;
- выбрать команду Вставить.
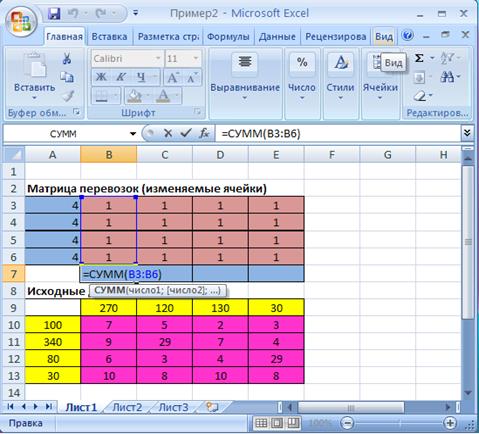
Рис.2.3. Экранная форма задачи (2.1) после суммирования ячеек B 3: B 6 (курсор в ячейке B 7)
Эту же последовательность действий выполнить для ячеек С7:Е7 или проделать следующее:
- поместить курсор в ячейку С7;
- выбрать команду Копировать;
- выделить ячейки С7:Е7;
- выбрать команду Вставить.
Таким образом, введены ограничения для всех поставщиков и всех потребителей (см.рис.2.4).
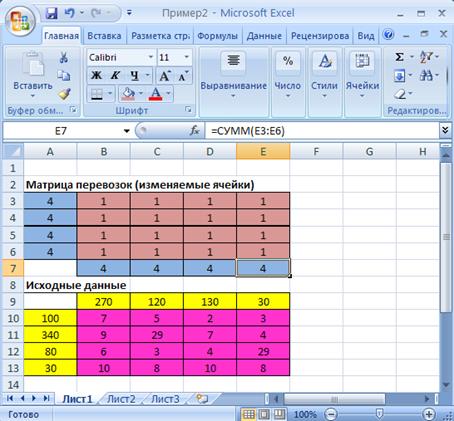
Рис.2.4. Экранная форма задачи (2.1) после введения всех ограничений
Назначение целевой функции
Для вычисления значения целевой функции, соответствующей минимальным суммарным затратам на доставку груза, необходимо зарезервировать ячейку и ввести формулу для ее вычисления:
Для этого необходимо произвести следующие действия:
- поместить курсор в ячейку В15 (после решения задачи в данной ячейке будет находиться значение целевой функции);
- запустить Мастер функций (значок fx );
- в окне Категория выбрать Математические;
- в окне Функция выбрать СУММПРОИЗВ;
- нажать кнопку ОК;
- в окне СУММПРОИЗВ указать адреса массивов, элементы которых обрабатываются этой функцией.
Целевая функция в задаче представляет собой произведение удельных затрат на доставку груза (расположенных в блоке ячеек В10÷Е13) и объемов поставок для каждого потребителя (содержимое ячеек ВЗ÷Е6). Для этого необходимо:
- в поле Массив 1 указать адреса ВЗ:Е6;
- в поле Массив 2 указать адреса В10:Е13;
- нажать кнопку ОК — подтверждение окончания ввода адресов массивов (см.рис.2.5.).
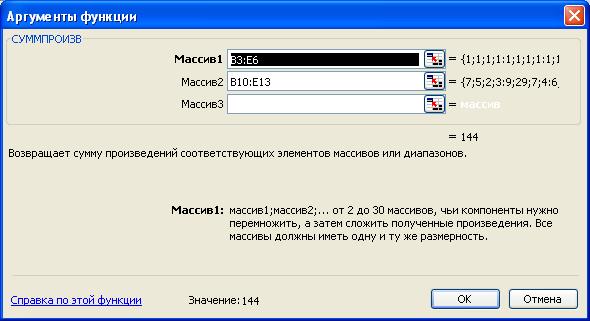
Рис.2.5. Ввод формулы для расчета ЦФ в окно Мастер функций
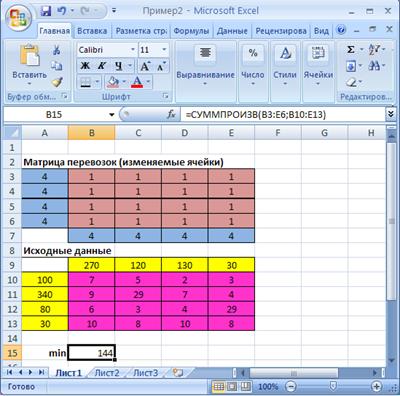
Рис.2.6. Экранная форма задачи (2.1) после ввода всех необходимых формул
В поле ячейки В15 появится числовое значение, равное произведению единичных поставок на удельные коэффициенты затрат по доставке грузов (в данной задаче — это число 144) (рис. 2.6.).
Ввод ограничений задачи
В матрицу перевозок, содержащую исходные данные по задаче, необходимо ввести условие реализации мощностей всех поставщиков (рис. 2.7):
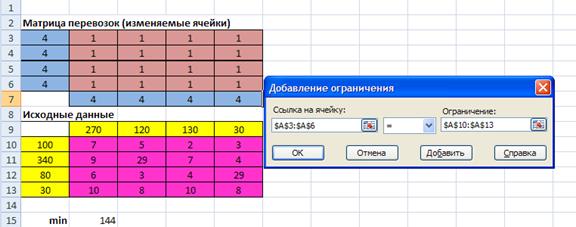
Рис.2.7. Добавление ограничений для поставщиков
- выбрать Добавить ограничения;
- в поле Ссылка на ячейку ввести адреса $А$3:$А$6;
- в среднем поле установить знак =;
- в поле Ограничение установить адреса $А$10:$А$13;
- для подтверждения введенного условия нажать кнопку ОК.
Далее вводится ограничение, которое реализует условие удовлетворения мощностей всех потребителей (рис. 2.8):
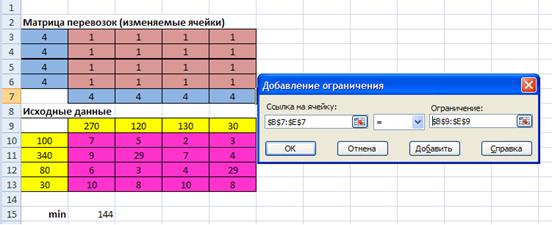
Рис.2.8. Добавление ограничений для потребителей
- выбрать Добавить ограничения;
- в поле Ссылка на ячейку ввести адреса $В$7:$Е$7;
- в поле знака выбрать знак =;
- в поле Ограничение установить адреса $В$9:$Е$9;
- нажать кнопку ОК;
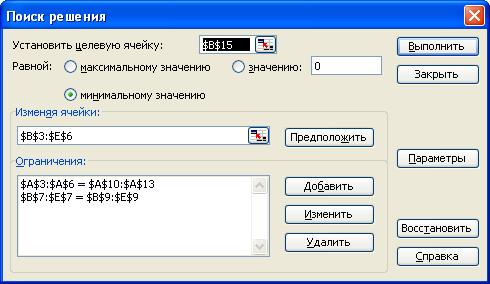
Рис.2.9. Ввод зависимостей из математической модели
- после этого надо вернуться в поле Поиск решения;
- после ввода всех ограничений ввести ОК. На экране появится окно Поиск решения с введенными ограничениями (рис. 2.9).
Ввод параметров
С помощью окна Параметры можно вводить условия для решения оптимизационных задач (см.рис.2.10.). В нашей задаче следует установить флажок Неотрицательные значения и флажок Линейная модель. Нажать кнопку ОК. Опять появится диалоговое окно Поиск решения. Далее необходимо:
- щелкнуть Параметры;
- выбрать переключатель Линейная модель;
- выбрать переключатель Неотрицательные значения (так как объемы поставок груза не могут быть отрицательными);
- нажать кнопку ОК. После этого произойдет переход в поле Поиск решения;
- нажать кнопку Выполнить.
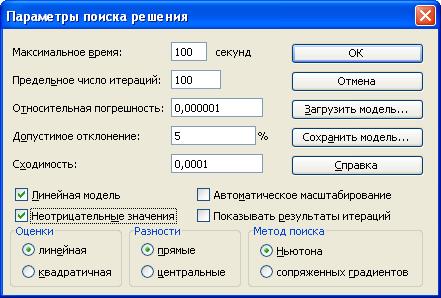
Рис.2.10. Параметры поиска решения транспортной задачи
Решение
Решение задачи выполняется сразу же после ввода данных, когда на экране находится диалоговое окно Поиск решения. Нажать кнопку Выполнить. На экране появится диалоговое окно Результаты поиска решения (рис.2.11).
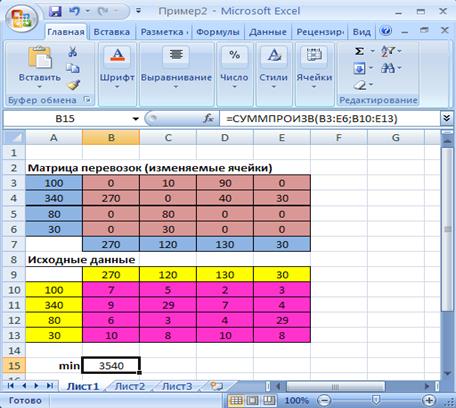
Рис.2.11. Диалоговое окно Результаты поиска решения
В результате нами был получен оптимальный план перевозок (табл.2.3).:
Матрица перевозок (изменяемые ячейки)
План перевозок означает, что:
Х12 = 10 ед. груза следует перевезти от поставщика 1 потребителю 2;
Х13 = 90 ед. груза следует перевезти от поставщика 1 потребителю 3;
X21 = 270 ед. груза следует перевезти от поставщика 2 потребителю 1;
Х23 = 40 ед. груза следует перевезти от поставщика 2 потребителю 3;
Х24 = 30 ед. груза следует перевезти от поставщика 2 потребителю 4;
Х32 = 80 ед. груза следует перевезти от поставщика 3 потребителю 2;
Х42 = 30 ед. груза следует перевезти от поставщика 4 потребителю 2.
Общая стоимость перевозок = 3540.
ВАРИАНТЫ
Используя MS Excel, найти решение для модели ЛП, соответствующей заданному варианту (табл.3.1.).
Варианты задач к лабораторной работе №1
| № варианта | Математическая модель |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 |
ВАРИАНТЫ
Используя MS Excel, найти решение ТЗ, соответствующей заданному варианту (табл.3.2.).
Однородный груз, имеющийся в m пунктах отправления (производства) А1, А2, . Аm соответственно в количествах а1, а2, . аm единиц, требуется доставить в каждый из n пунктов назначения (потребления) В1, В2, . Вn соответственно в количествах b1, b2, …, bn единиц. Стоимость перевозки сij (тариф) единицы продукции из Аi в Bj известна для всех маршрутов. Требуется составить такой план перевозок, при котором весь груз из пунктов отправления вывозится и запросы всех пунктов потребления удовлетворяются.
СКАЧАТЬ: metody-optimizacii.rar [308,62 Kb] (cкачиваний: 95)
Лабораторная работа №1
"Решение задач линейного программирования с использованием Microsoft Excel”
ЦЕЛЬ РАБОТЫ: Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.
1 ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1.1 Использование Microsoft Excel для решения задач ЛП
Для того чтобы решить задачу ЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.
1. Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
• переменных,
• целевой функции (ЦФ),
• ограничений,
• граничных условий;
b) ввести исходные данные в экранную форму:
• коэффициенты ЦФ,
• коэффициенты при переменных в ограничениях,
• правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
• формулу для расчета ЦФ,
• формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне "Поиск решения"):
• целевую ячейку,
• направление оптимизации ЦФ;
e) ввести ограничения и граничные условия (в окне "Поиск решения"):
• ячейки со значениями переменных,
• граничные условия для допустимых значений переменных,
• соотношения между правыми и левыми частями ограничений.
2. Решить задачу:
a) установить параметры решения задачи (в окне "Поиск решения");
b) запустить задачу на решение (в окне "Поиск решения");
c) выбрать формат вывода решения (в окне "Результаты поиска решения").
1.2 Одноиндексные задачи ЛП
Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:
(1.1)
1.2.1. Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода условий задачи (1) вместе с введенными в нее исходными данными представлена на рисунке1.
Рисунок 2 – Окно "Поиск решения" задачи
Рисунок 3 – Экранная форма задачи после ввода всех необходимых формул
1.3 Целочисленное программирование
При целочисленном программировании мы получим те же результаты, так как в строке значение у нас уже целые коэффициенты.
1.4 Двухиндексные задачи ЛП
Двухиндексные задачи ЛП вводятся и решаются в Excel аналогично одноиндексным задачам. Специфика ввода условия двухиндексной задачи ЛП состоит лишь в удобстве матричного задания переменных задачи и коэффициентов ЦФ.
Рисунок 4 – Ограничения и граничные условия задачи
Рисунок 5 – Экранная форма после получения решения задачи
1.5 Задачи с булевыми переменными
Частным случаем задач с целочисленными переменными являются задачи, в результате решения которых искомые переменные могут принимать только одно из двух значений: 0 или 1. Такие переменные в честь предложившего их английского математика Джорджа Буля называют булевыми. На рис.6 представлена экранная форма с решением некоторой двухиндексной задачи с булевыми переменными.
Рисунок 6 – Решение двухиндексной задачи с булевыми переменными
В задаче с булевыми переменными в окне "Поиск решения" добавить граничные условия, имеющие смысл ограничения значений переменных по их единичной верхней границе.
Рисунок 7 – Добавление условия единичной верхней границы значений переменных двухиндексной задачи с булевыми переменными.
1. Каковы основные этапы решения задач ЛП в MS Excel?
Для того чтобы решить задачу ЛП в табличном редакторе MicrosoftExcel, необходимо выполнить следующие действия.
1. Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
• переменных,
• целевой функции (ЦФ),
• ограничений,
• граничных условий;
b) ввести исходные данные в экранную форму:
• коэффициенты ЦФ,
• коэффициенты при переменных в ограничениях,
• правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
• формулу для расчета ЦФ,
• формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне "Поиск решения"):
• целевую ячейку,
• направление оптимизации ЦФ;
e) ввести ограничения и граничные условия (в окне "Поиск решения"):
• ячейки со значениями переменных,
• граничные условия для допустимых значений переменных,
• соотношениямежду правыми и левыми частями ограничений.
2. Решить задачу:
a) установить параметры решения задачи (в окне "Поиск решения");
b) запустить задачу на решение (в окне "Поиск решения");
c) выбрать формат вывода решения (в окне "Результаты поиска решения").
2. Каков вид и способы задания формул для целевой ячейки и ячеек левых частей ограничений?
Формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B6, C6, D6, E6), то есть
=СУММПРОИЗВ(B$3:E$3;B6:E6)
Существует другой способ задания функций в Excel с помощью режима "Вставка функций", который можно вызвать из меню "Вставка" или при нажатии кнопки " "на стандартной панели инструментов. Так, например, формулу (1.4) можно задать следующим образом:
курсор в поле F6;
• нажав кнопку " ",вызовите окно"Мастер функций – шаг 1 из 2";
• выберите в окне "Категория" категорию "Математические";
• в окне "Функция" выберитефункцию СУММПРОИЗВ;
• в появившемся окне "СУММПРОИЗВ" в строку "Массив 1" введите выражение B$3:E$3, а в строку "Массив 2" – выражение B6:E6 (рис.1.3);
• после ввода ячеек в строки "Массив 1" и "Массив 2" в окне "СУММПРОИЗВ" появятся числовые значения введенных массивов (см. рис.1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, C10, D10, E10 – 1-е ограничение; B11, C11, D11, E11 – 2-е ограничение и B12, C12, D12, E12 – 3-е ограничение).
3. В чем смысл использования символа $ в формулах MS Excel?
Символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится.
4. В чем различие использования в формулах MS Excel символов ; и : ?
Символ: означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия. Символ;используется для разделения массивов.
5. Почему при вводе формул в ячейки ЦФ и левых частей ограничений в них отображаются нулевые значения?
В экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
6. Каким образом в MS Excel задается направление оптимизации ЦФ?
В окне поиска решения.
7. Какие ячейки экранной формы выполняют иллюстративную функцию, а какие необходимы для решения задачи?
Ячейки, которые не используются для вычисления ограничений или ЦФ (например, заголовки или ячейки со знаками равенства) выполняют иллюстративную функцию.
12. Объясните смысл параметров, задаваемых в окне "Параметры поиска решения".
• Параметр "Максимальное время" служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
• Параметр "Предельное числоитераций"служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
• Параметр "Относительная погрешность" служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
• Параметр "Допустимое отклонение" служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
• Параметр "Сходимость" применяется только при решении нелинейных задач.
• Установка флажка "Линейная модель" обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
• Подтвердите установленные параметры нажатием кнопки "OK".
13. Каковы особенности решения в MS Excel целочисленных задач ЛП?
Добавилось требование целочисленности значений всех переменных. В этом случае в поиске решения добавляем требование целочисленности функции.
14. Каковы особенности решения в MS Excelдвухиндексных задач ЛП?
Двухиндексные задачи ЛП вводятся и решаются в Excel аналогично одноиндексным задачам. Специфика ввода условия двухиндексной задачи ЛП состоит лишь в удобстве матричного задания переменных задачи и коэффициентов ЦФ.
15. Каковы особенности решения в MS Excel задач ЛП с булевыми переменными?
Частным случаем задач с целочисленными переменными являются задачи, в результате решения которых искомые переменные могут принимать только одно из двух значений: 0 или 1. В окне "Поиск решения" добавить граничные условия, имеющие смысл ограничения значений переменных по их единичной верхней границе (рис.1.19).
Приобретение навыков решения задач линейного программирования (ЛП)в табличном редакторе Microsoft Excel.
Порядок выполнения работы
Для модели линейного программирования, соответствующей номеру Вашего варианта (вариант соответствует номеру списка в вашей подгруппе), найдите оптимальное решение в табличном процессоре Microsoft Excel и продемонстрируйте его преподавателю.
Пример решения задачи линейного программирования
Рассмотрим пример нахождения решения для следующей задачи ЛП

В экранной форме на рис. 3.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП. В ячейку F6, в которой будет отображаться значение целевой функции (ЦФ), необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (3.1) значение ЦФ определяется выражением

Используя обозначения соответствующих ячеек в Excel (см. рис. 3.1), формулу для расчета ЦФ (3.2) (ячейка F6) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B6, C6, D6, E6), то есть

Чтобы задать формулу (3.3) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу "Enter"

где символ "$" перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится; символ ":" означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия. После этого в целевой ячейке появится 0 (нулевое значение) (рис. 3.2).
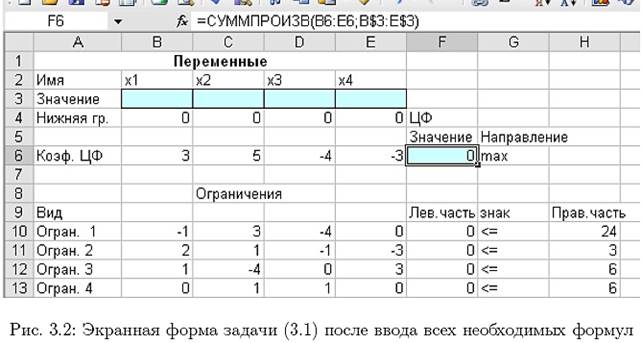
Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима "Вставка функций", который можно вызвать из меню "Вставка" или при нажатии кнопки "fx" на стандартной панели инструментов. Так, например, формулу (3.4) можно задать следующим образом:
• курсор в поле F6;
• выберите в окне "Категория" категорию "Математические";
• в окне "Функция" выберите функцию "СУММПРОИЗВ";
• в появившемся окне "СУММПРОИЗВ" в строку "Массив 1" введите выражение B$3:E$3, а в строку "Массив 2" — выражение B6:E6 (рис. 3.3);

• после ввода ячеек в строки "Массив 1" и "Массив 2" в окне "СУММПРОИЗВ" появятся числовые значения введенных массивов (см. рис. 3.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
Левые части ограничений задачи (3.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3,D3, E3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, C10, D10, E10 — 1-е ограничение; B11, C11, D11, E11— 2-е ограничение и т.д. Формулы, соответствующие левым частям первых двух ограничений, представлены в табл. 3.1.

Как видно из табл. 3.1, формулы, задающие левые части ограничений задачи (3.1), отличаются друг от друга и от формулы (3.4) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений.
Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню "Сервис" (рис. 3.4):

• поставьте курсор в поле "Установить целевую ячейку";
• введите адрес целевой ячейки $F$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме — это будет равносильно вводу адреса с клавиатуры;
• введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке "максимальному значению";
• в окно "Поиск решения" в поле "Изменяя ячейки" впишите адреса $B$3:$E$3.
Необходимые адреса можно вносить в поле "Изменяя ячейки" и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю(см. рис. 3.1).

• В поле "Ссылка на ячейку" введите адреса ячеек переменных $B$3:$E$3. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме.
• В поле "Ограничение" введите адреса ячеек нижней границы значений переменных, то есть $B$4:$E$4. Их также можно ввести путем выделения мышью непосредственно в экранной форме.
• В поле "Ссылка на ячейку" введите адрес ячейки левой части конкретного ограничения, например $F$10. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме.
• В соответствии с условием задачи (3.1) выбрать в поле знака необходимый знак.
• В поле "Ограничение" введите адрес ячейки правой части рассматриваемого ограничения, например $H$10.
• Аналогично введите ограничения: $F$11>=$H$11, $F$12<=$H$12.
• Подтвердите ввод всех перечисленных выше условий нажатием кнопки OK.
Окно "Поиск решения" после ввода всех необходимых данных задачи (3.1)представлено на рис. 3.4.
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки "Изменить" или "Удалить" (см. рис. 3.4).
Задача запускается на решение в окне "Поиск решения". Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку "Параметры" и заполнить некоторые поля окна "Параметры поиска решения" (рис. 3.6).

Параметр "Максимальное время" служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32767 секунд (более 9 часов).
Параметр "Предельное число итераций" служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32767 .
Параметр "Относительная погрешность" служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1 . Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр "Допустимое отклонение" служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр "Сходимость" применяется только при решении нелинейных задач.
Установка флажка "Линейная модель" обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки "OK".
Запуск задачи на решение производится из окна "Поиск решения" путем нажатия кнопки "Выполнить".


В окне "Результаты поиска решения" представлены названия трех типов отчетов: "Результаты "Устойчивость "Пределы". Они необходимы при анализе полученного решения на чувствительность. Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку "OK". После этого в экранной форме появляется оптимальное решение задачи (рис. 3.10).

Цель: научиться решать задачи линейного программирования в Excel с помощью надстройки «Поиск решения».
Краткие теоретические сведения
Оптимизационные задачи находят широкое применение в различных областях практической деятельности: при организации работы транспортных систем, в управлении промышленными предприятиями, при составлении проектов сложных систем. Многие распространенные классы задач системного анализа, в частности, задачи оптимального планирования, распределения различных ресурсов, управления запасами, календарного планирования, межотраслевого баланса укладываются в рамки моделей линейного программирования.
Постановка задачи линейного программирования (ЗЛП).
Имеется множество переменных X= (x1, х2. хn). Целевая функция линейно зависит от управляемых параметров:

(1)
Имеются ограничения, которые представляют собой линейные формы
где (2)
Требуется определить максимум (минимум) линейной функции
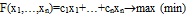
(3)
при условии, что точка (х1, х2. хn) принадлежит некоторому множеству D, которое определяется системой линейных неравенств
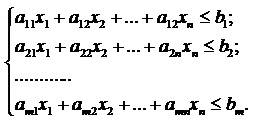
(4)
Любое множество значений (х1*, х2*. хn*), которое удовлетворяет системе неравенств (4) задачи линейного программирования, является допустимым решением данной задачи. Если при этом выполняется неравенство
для всего множества значений x1, х2. хn, то значение х1 o ..хn o является оптимальным решением задачи линейного программирования.
Пример построения математической модели и решения ЗЛП.
Задача. Требуется определить, в каком количестве надо выпускать продукцию четырех типов A, B, C иD, для изготовления которой требуются ресурсы трех видов: трудовые, сырье и финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в таблице1. Там же приведено наличие располагаемого ресурса.
Ресурс
наличие
Составим математическую модель, для чего введем следующие обозначения:
xi - количество выпускаемой продукции i-го типа, i = 1,2,3,4
bj –количество располагаемого ресурса j-го вида, j = 1,2,3
aji – норма расхода j-го ресурса для выпуска i-ой продукции
ci – прибыль от реализации единицы продукции i-го типа.
Как видно из таблицы 1, для выпуска единицы продукции A требуется 6 единиц сырья, значит, для выпуска всей продукции A требуется 6x1 единиц сырья, где x1 - количество выпускаемой продукции A. С учетом того, что для других видов продукции зависимости аналогичны, ограничение по сырью будет иметь вид:
В этом ограничении левая часть равна величине требуемого ресурса, а правая часть показывает количество имеющегося ресурса.
Аналогично можно составить ограничения для других видов ресурсов и написать зависимость для целевой функции. Тогда математическая модель задачи будет иметь вид:
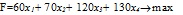
1. Для ввода условий задачи создадим форму в Excel (рис.1). В ячейках B3:E3 будут отображаться вычисленные значения xi.

рис.1. Форма для ввода условий задачи
2. Введем коэффициенты целевой функции и ограничений в форму. Из математической модели введем зависимости. Введенные данные отображены на рис.2.

рис.2. Исходные данные задачи

В ячейке F6 записана формула целевой функции, в F9-F11- левые части ограничений из математической модели. На рис. 3 отображен режим представления формул. Перейти к данному режиму можно с помощью последовательности действий: нажмите кнопку Microsoft Office, щелкните Параметры Excel, откройте вкладку Дополнительно и установите флажок Показывать формулы, а не их значения.

рис.3. Режим представления формул.
4. В поле Установить целевую ячейку введем ссылку на целевую ячейку, для чего установим курсор в поле и щелкнем левой кнопкой мыши по ячейке F6.
5. Выберем направление поиска, установив флажок равной максимальному значению.
6. Установим курсор в поле Изменяя ячейки и введем с помощью мыши имена изменяемых ячеек B3:E3. В этих ячейках в результате поиска решения будет выведено решение – значения переменных xi., при которых целевая функция имеет максимальное значение при заданных ограничениях.
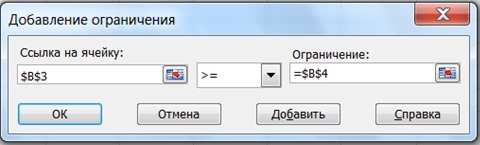
Рис.4. Окно добавления ограничений.
На рисунке 5 показано заполненное окно Поиск решения.

Рис.5 Заполненное окно Поиск решения
8. Далее нажимаем на кнопку Выполнить. Появляется диалоговое окно Результаты поиска решения (рис.6). Решение найдено. Все ограничения и условия оптимальности выполнены. Сохраняем найденное решение. В этом окне также можно получить три вида отчетов: по результатам, устойчивости и пределам, отчеты формируются в новых рабочих листах.

рис.6. Окно Результаты поиска решения
Результаты оптимального решения задачи приведены в таблице (рис.7).
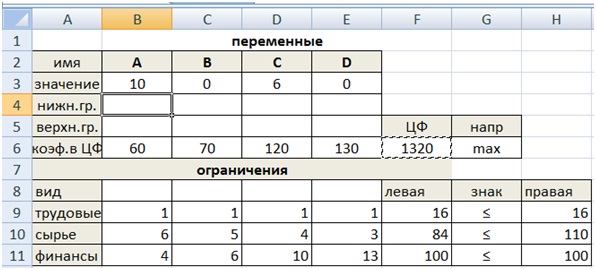
рис.7. Результаты оптимального решения
Таким образом, получилось оптимальное решение (10;0;6;0), т.е. целесообразно выпускать 10 единиц продукции А и 6 единиц продукции С. Максимальная прибыль равна 1320 денежным единицам, при этом используются все трудовые и финансовые ресурсы, 84 единиц сырья, в запасе остается 26 единиц сырья.
Задания для лабораторной работы.
Составить математическую модель и решить полученную задачу линейного программирования в Excel с помощью надстройки Поиск решения.
Для перевозки грузов используются машины типов А и Б. Грузоподъемность машин обоих типов одинаковая и равна h т. За одну ходку машина А расходует а11кг смазочных материалов и а12л горючего, машина Б - а21 кг смазочных материалов иа22л горючего. На базе имеется d1кг смазочных материалов и d2л горючего. Прибыль от перевозки одной машины А составляет с1руб., машины Б - с2руб. Необходимо перевезти H т груза (исходные данные приведены в нижеследующей таблице).
Сколько надо использовать машин обоих типов, чтобы доход от перевозки груза был максимальным.
Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе MicrosoftExcel.
1.2. Порядок выполнения работы
Для модели ЛП, соответствующей номеру вашего варианта, найдите оптимальное решение в табличном редакторе MicrosoftExcelи продемонстрируйте его преподавателю.
1.3. Инструкция по использованию MicrosoftExcelДля решения задач лп
Поиск решения– это надстройкаExcel, которая позволяет решать оптимизационные задачи. Если в менюДанныеотсутствует командаПоиск решения, значит, необходимо загрузить эту надстройку. Выберите кнопку“Office”Параметры Excel Надстройкии активизируйте надстройкуПоиск решения.
Для того чтобы решить задачу ЛП в табличном редакторе MicrosoftExcel, необходимо выполнить следующие действия.
Ввести условие задачи:
создать экранную форму для ввода условия задачи:
целевой функции (ЦФ),
ввести исходные данные в экранную форму:
коэффициенты при переменных в ограничениях,
правые части ограничений;
ввести зависимости из математической модели в экранную форму:
формулу для расчета ЦФ,
формулы для расчета значений левых частей ограничений;
задать ЦФ(в окнеПоиск решения):
направление оптимизации ЦФ;
ввести изменяемые ячейки и ограничения(в окнеПоиск решения):
ячейки со значениями переменных,
соотношения между правыми и левыми частями ограничений;
ввести параметры для решения задачи(в окнеПоиск решения):
линейная модель (для применения симплекс-метода),
неотрицательные значения переменных.
Решить задачу:
запустить задачу на решение(в окнеПоиск решения);
выбрать формат вывода решения(в окнеРезультаты поиска решения).
1.3.1. Одноиндексные задачи лп
Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:

1.3.1.1. Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис.1.1.

Рис.1.1. Экранная форма задачи (1.1) (курсор в ячейке D4)
Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ
В ячейку D4, в которой будет отображаться значение ЦФ, необходимо ввестиформулу,по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением

Используя обозначения соответствующих ячеек в Excel (см. рис.1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B4, C4), то есть

Чтобы задать формулу (1.3) необходимо в ячейку D4ввести следующее выражение и нажать клавишуEnter
=СУММПРОИЗВ($B$3:$C$3;B4:C4),
где символ $перед номером строки 3 означает, что при копировании этой формулы в другие места листаExcelномер строки 3 не изменится, а символ$перед названием столбцаBозначает, что при копировании этой формулы в другие места листаExcelномер столбцаBне изменится;
символ: означает, что в формуле будут использованы всеячейки, расположенные между ячейками, указанными слева и справа от двоеточия. После этого в целевой ячейке появится 0 (нулевое значение) (рис.1.2).

Рис.1.2. Экранная форма задачи (1.1) после ввода всех необходимых формул
(курсор в ячейке D4)

Примечание 1.1.Существует другой способ задания функций вExcelс помощью режимаВставка функций, который можно вызвать из менюВставкаили при нажатии кнопки на стандартной панели инструментов. Так, например, формулу (1.4) можно задать следующим образом:
курсор в поле D4;

нажав кнопку , вызовите окноМастер функций – шаг 1 из 2;
выберите в окне Категория категориюМатематические;
в окне Функция выберите функцию СУММПРОИЗВ;
в появившемся окне СУММПРОИЗВв строкуМассив 1введите выражение$B$3:$C$3, а в строкуМассив 2– выражениеB4:C4 (рис.1.3);
после ввода ячеек в строки Массив 1иМассив 2в окнеСУММПРОИЗВпоявятся числовые значения введенных массивов (см. рис.1.3), а в экранной форме в ячейкеD4появится текущее значение, вычисленное по введенной формуле, то есть 0, так как в момент ввода формулы значения переменных задачи нулевые.

Рис.1.3. Ввод формулы для расчета ЦФ в окно СУММПРОИЗВ
Зависимости для левых частей ограничений
Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B7, C7 – 1-е ограничение; B8, C8 – 2-е ограничение и B9, C9 – 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл.1.1.
Читайте также:


