Как в ворде сделать треугольник паскаля

Обновлено: 23.01.2025

Этим фактом и воспользуемся. Только в Excel удобней использовать не классический (построчный) вид треугольника Паскаля, а такой:

Здесь биномиальные коэффициенты выписаны по диагонали, в первой заполненной строке и первом заполненном столбце единицы, а в остальных сумма вехнего и левого элемента.

Перейдем к построению. Для нас достаточно выписывать не коэффициенты, а только их четность.

Для начала сделаем размер ячеек в Excel, к примеру 7 на 7 пикселей.

Станем в ячейку B2, затем выделим область B2:DY129 — для этого нажимаем Ctrl + G и в поле ссылка пишем B2:DY129.

Теперь в строке формул пишем =ЕСЛИ(ИЛИ(СТРОКА()=2;СТОЛБЕЦ()=2);1;ОСТАТ(A2+B1;2))

и нажимаем Ctrl + Enter, чтобы заполнить подобной формулой всю выделенную область.

Заходим Меню — Условное форматирование и для значения 1 указываем цвет ячейки.

В итоге получаем:

Следует отметить, что треугольник Серпинского получается при некоторой разновидности случайного блуждания на плоскости. А именно:

Зафиксируем на плоскости 3 вершины треугольника и возьмем еще одну точку.
Первую точку получим как середину отрезка между случайно выбранной вершиной и точкой из п.1.
Вторую точку получим как середину отрезка между случайно выбранной вершиной и первой точкой.
…
Повторяем процесс много раз.

Можно ипользовать такой макрос:

Public Sub Макрос()

Dim arRange(1 To 3) As Range

Dim tekRow As IntegerDim tekColumn As IntegerDim i As IntegerDim iT As Integer
tekRow = Int(1000 * Rnd) + 1

tekColumn = Int(200 * Rnd) + 1
Set arRange(1) = Cells(1, 1)

Set arRange(2) = Cells(50, 250)Set arRange(3) = Cells(200, 20)
Cells.Clear

For i = 1 To 20000

iT = (Int(1000 * Rnd) Mod 3) + 1 tekRow = Int((tekRow + arRange(iT).Row) / 2) tekColumn = Int((tekColumn + arRange(iT).Column) / 2) Cells(tekRow, tekColumn).Interior.ColorIndex = 5Next
End Sub

Сначала запишите число 1.

Поместите еще две единицы, чтобы начать построение следующей строки.

Теперь вам нужно узнать, как построить нижележащие строки, следующие за двумя первыми, содержащими только единицы. В каждой новой строке количество элементов будет на один больше, чем в предыдущей. Каждая строка начинается и заканчивается числом 1.

Найдите внутреннее число, используя числа, расположенные выше него. Каждый внутренний элемент может быть вычислен путем сложения двух чисел, расположенных выше него. Например, в середине третьей строки мы помещает число 2 (1+1=2).

По мере заполнения строк треугольника, вы сможете заметить множество интересных свойств треугольника Паскаля.

Первое и последнее число в каждой строке равны 1. Второе и предпоследнее — натуральные числа, третье в строке — треугольное число.
Сумма чисел каждой строки (номер строки указан) равна числу 2, возведенному в степень, равную номеру этой строки (основание степени равно 2).
Принимая во внимание, что первое число в каждой строке является нулевым элементом и равно 1, если вы возьмете следующее число в ряду и разделите все другие элементы в этой строке, вы увидите, что все элементы нацело делятся на номер данной строки.
За исключением некоторых случаев, каждая линия в треугольнике Паскаля имеет прямой эффект, который проявляется при возведении любого основания в степень, соответствующую номеру строки. В некоторых строках, где следующая ячейка содержит одно или больше чисел на ячейку, разряд десятков суммируется с числом в ячейки слева.
Треугольник Паскаля симметричен..

Наименование:

Информация:

Описание (план):

С одним из видов числовой последовательности мы встречаемся в биологии. Число образовавшихся клеток при митозе и мейозе изменяется как n-й член геометрической прогрессии со знаменателем 2 и 4 соответственно. В литературе, при изучении стихотворных метров, на помощь приходит арифметическая прогрессия. Например, ямб – стихотворный метр с акцентами на чётных слогах стиха. Номера ударных слогов (второй, четвёртый, шестой, восьмой и т. д.) образуют арифметическую прогрессию с первым членом два и разностью, равной двум. Числовые последовательности нашли своё применение и в экономике. Так, при подсчёте банковского процента нам помогает арифметическая и геометрическая прогрессии. Если смотреть на листья растения сверху, можно заметить, что они распускаются по спирали. Углы между соседними листьями образуют правильный математический ряд, известный под названием последовательности Фибоначчи. Благодаря этому каждый отдельно взятый лист, растущий на дереве, получает максимально доступное количество тепла и света. В природе последовательность Фибоначчи можно проследить на примерах спирального развития сегментов раковины и лепестков подсолнуха, расходящихся лучами из одной точки в центре цветка. в строении нашего тела, в ботанике, в процессах квантовой механики, в практической деятельности людей, она нашла широкое научное применение в математике, технике, музыке, эстетике и пр.
В своей курсовой работе я приведу примеры использования программных средств компьютера при работе с числовыми последовательностями.

Фигурные числа в треугольнике Паскаля.

В математике существует множество последовательностей, упакованных в одну форму. Примером может являться треугольник Паскаля.
Треугольник Паскаля часто записывают в виде равнобедренного треугольника, в котором на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ним слева и справа в предшествующей строке. Треугольник можно продолжать неограниченно. Он обладает симметрией относительно вертикальной оси, проходящей через его вершину.

Треугольник Паскаля прост, но в то же время таит в себе неисчерпаемые сокровища и связывает воедино различные разделы математики, не имеющие на первый взгляд ничего общего. Отметим лишь некоторые из основных свойств.
Каждый элемент является биномиальным коэффициентом. Именно это фундаментальное свойство треугольника Паскаля связывает его не только с комбинаторикой и теорией вероятностей, но и другими областями математики и ее приложений, вдоль диагоналей, параллельных сторонам треугольника, выстроены треугольные числа и их обобщения на случай пространств всех размерностей.
В этой части курсовой работы поставлена следующая задача: задать треугольник Паскаля с помощью Microsoft Office Excel и показать ряд интересных свойств этого треугольника.
Для этого в столбце А укажем номер строки треугольника: строки нумеруются сверху вниз, начиная с нуля. В столбец В заполним нулями. Вершина треугольника находится в ячейке С1, значение которой равно 1. С помощью сложения двух соседних элементов предыдущей строки заполняем строку 2(к=1). Для этого в ячейку С2 записываем формулу вычисления В1+С1 и переносим ее на соседнюю ячейку.

Растянув формулы по строкам и столбцам получаем треугольник Паскаля:

Пользуясь возможностями Excel, не проводя вычислений, рассмотрим некоторые свойства треугольника Паскаля. Рассмотрим значения треугольника находящиеся в столбцах. Очевидно, что столбец D содержит натуральный ряд. Столбец Е – ряд треугольных чисел. Покажем это.
Треугольное число — это число кружков, которые могут быть расставлены в форме равностороннего треугольника.

Последовательность треугольных чисел Тn для n = 0, 1, 2, … начинается так:
0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, …
n-ый член последовательности треугольных чисел можно задать так: Tn=1+2+3+…+n
Покажем, что в треугольнике Паскаля действительно есть последовательность треугольных чисел:
Tn=E(n+1)=D(n)+E(n)= D(n)+ D(n-1)+E(n-1)=…=
=Dn+D(n-1)+…+D1+E1=0+1+2+…+n-2+n-1+n.
Так как ряд начинается с ячейки E2 со значением 0, то для шестого члена последовательности имеем: T6=E7=1+2+…+6=15.
Соседний столбец, столбец F заполнен элементами последовательности тетраэдрических чисел Sn: 0,1,4,10, 24,36,… Эти числа показывают, сколько шаров может быть уложено в виде треугольной пирамиды (тетраэдра).

Известно, что каждый член этой последовательности может быть описан с помощью треугольных чисел: Sn= T1+T2+…+Tn. Действительно, геометрически это можно показать так:

В нашем случае элемент Sn расположен в ячейке по адресу F(n+2)=E(n+1)+F(n+1)=E(n+1)+En+Fn=…=E(n+1)+En+…+E2= Tn+Tn-1+…+T1
Есть еще одна последовательность фигурных чисел, которая может быть выражена с помощью треугольных чисел: квадратная. Kn=Tn+Tn-1. Элементы этой последовательности найдем с помощью Exsel. Задав для элементов столбца F формулу Fn=En+E(n-1) получаем элементы последовательности квадратных чисел.

Геометрически такие числа могут быть представлены в виде площади квадрата с целочисленной стороной.

Пространственно из этих чисел получаются пирамиды с четырехугольником в основании.

Назовем последовательность таких чисел пирамидальной-4 Pn. Приведем пример:

Pn=K1+K2+…+Kn=T1+(T1+T2)+(T2+T3)+…+(Tn-2+Tn-1)+(Tn-1+Tn)+Tn=
=(T1+T2+…+Tn-1)+(T1+T2+…+Tn-1+Tn)=Sn-1+Sn
Итак, представим в Excel все разобранные выше последовательности фигурных чисел.

Изучение элементов теории фигурных чисел на занятиях по математике в старших классах средней школы не только возможно, но и крайне желательно: обширный исторический материал, расцвеченный увлекательными легендами и мифами, способствует повышению интереса к предмету, интересные геометрические конструкции выполняют пропедевтическую роль, готовя старшеклассников к изучению современной дискретной математики, в частности теории графов.
Задание треугольника Паскаля в Excel делает доступным мгновенное вычисление любого элемента, позволяет убедиться во множестве его свойств.

Узоры таблицы Пифагора

Впервые таблица Пифагора примерно в том же виде, в каком ее печатают на обложках школьных тетрадей, но в ионийской нумерации, появилась в сочинении неопифагорейца Никомаха Геразского (I-II вв. н. э.) «Введение в арифметику». По словам Никомаха, эта таблица восходит «к самому Пифагору». Еще более древние таблицы умножения обнаружены на месопотамских глиняных табличках — их «возраст» около 5 тысяч лет. Таблицу Пифагора можно расширять вправо и вниз до бесконечности, соблюдая единственное условие: каждое число таблицы есть произведение номера строки и номера столбца, в которых оно стоит.
Расширенные таблицы умножения существуют давно. Так, например, в первой печатной математической книге на русском языке «Считание удобное, которым всякий человек, купующий или продающий, зело удобно изыскати может число всякие вещи» (Москва, 1682) имеется таблица умножения чисел от 1×1 до 100×100.
Таблица умножения скрывает в себе много замечательных математических закономерностей, поиск которых способен превратиться в увлекательное занятие, сулящее немало сюрпризов.
К изучению свойств расширенной таблицы Пифагора можно привлечь компьютер. Каждое число таблицы изобразим точкой (или клеткой) координатной плоскости монитора и в соответствии со свойствами чисел окрасим точки каким-либо цветом. Это реализуется с помощью шаблона программы, написанной на языке Turbo Basic version 1.1.
screen 12
for n=1 to 120
for m=1 to 120
p=m*n
line (4*n,4*m)-(4*n+2,4*m+2),15,bf
if условие then line (4*n,4*m)-(4*n+2,4*m+2),1,bf
next m,n
При исполнении программы каждое число p расширенной таблицы Пифагора 120×120, находящееся на пересечении n-го столбца и m-й строки, будет изображаться белой клеткой, а числа, удовлетворяющие заданному в программе условию, — синими.
Так, на рис. 1 (программа 1) синим цветом выделены квадратные числа таблицы Пифагора: 1, 4, 9, 16, …, n2,… , зеленым — треугольные: 1, 3, 6, 10, …, 1/2 n(n+1),… красным — числа одновременно и квадратные и треугольные: 1, 36, 1225, 41616 и т.д.
Чтобы получить представление о том, как в таблице Пифагора расположены числа, дающие одинаковые остатки при делении, например на 5, закрасим числа, дающие остатки 0, 1, 2, 3, 4, каждое своим цветом. Как это ни удивительно, но таблица Пифагора оказывается расчленен ной на совершенно одинаковые по раскраске квадраты (рис. 2, программа 2).
Аналогичное разбиение получается при делении чисел таблицы на любое другое натуральное число k, в чем легко убедиться, заменив в программе число 5 на него.
Благодаря свойству периодичности таблицы Пифагора по остаткам на экране возникают разнообразные мозаики. Очевидно, чем больше k, тем больше будет остатков r, тем больше потребуется цветов. Чтобы узоры не были слишком пестрыми, ограничимся, например, тремя цветами. Для этого остатки сгруппируем по модулю 3, то есть первым цветом закрасим числа таблицы с остатками 1, 4, 7, 10. вторым — числа с остатками 2, 5, 8, 11. а третьим — числа, кратные 3 (рис.3, программа 3).
Можно расчленить любую из этих мозаик на три одноцветные, дополняющие одна другую до полной мозаики. Каждая из них в отдельности тоже представляет интерес (рис.4, программа 4).
Еще один вариант трехцветных мозаик приведен на рис. 5 (программа 5). Здесь для большей симметрии одинаковым цветом закрашены не только числа с одинаковым остатком r, но и числа с остатком, дополняющим r до k.
Интересные мозаики возникают и тогда, когда красят не все числа, а выборочно. Например, трехцветный узор на рис. 6 (программа 6). Кружевной монохромный узор (рис.7, программа 7) возникает, если во всей таблице закрасить одинаковым цветом только числа, дающие остатки, сравнимые с одним и тем же натуральным числом.
А если в программу включить генератор случайных чисел для определения размеров квадратов k, лежащих в периоде номеров расширенной таблицы Пифагора и номеров цвета c, то с помощью компьютера таблица превратится в своеобразный калейдоскоп удивительных и неповторяющихся узоров (рис. 8, программа 8).
На рис. 9 (программа 9) показано, как в таблице Пифагора 32×32 чередуются числа нечетных и четных сотен. Здесь каждое число изображено клеткой синего или зеленого цвета. Причем числа первой, третьей, пятой и т. д. сотни закрашены синим, а числа второй, четвертой, шестой и т.д. — зеленым. Ясно, что если произведение n x m постоянно, то между числами существует обратная пропорциональность, поэтому чередующиеся синие и зеленые полосы имеют гиперболическую форму.
С увеличением произведения n x m ширина полос уменьшается, а затем полосы и вовсе разрываются и распадаются на одноцветные островки, которые группируются с островками того же цвета, но из другой сотни, образуя симметричные формы (рис. 10, программа 10). Здесь каждое число таблицы 480×480 изображено точкой-пикселем.
Занимаясь изучением свойств таблицы Пифагора, можно отыскать новые, не менее красивые узоры на основе этой древней числовой схемы.

* Примечание. Уникальность работы указана на дату публикации, текущее значение может отличаться от указанного.

Пример для версии Microsoft Office Word 2016. В других должно работать аналогично.

Для вставки значка треугольника нужно воспользоваться специальными символами. Известно, что треугольник можно просто нарисовать, используя возможности векторного редактора Microsoft Office Word. Для вставки треугольника нужно выполнить следующие действия:

1. Идем в «Вставка → Символ → Другие символы».

2. Напротив текста «Код знака:» (чтобы долго не искать) вводим в поле цифры 2206 и нажимаем «Вставить». Готово, наш символ добавлен.

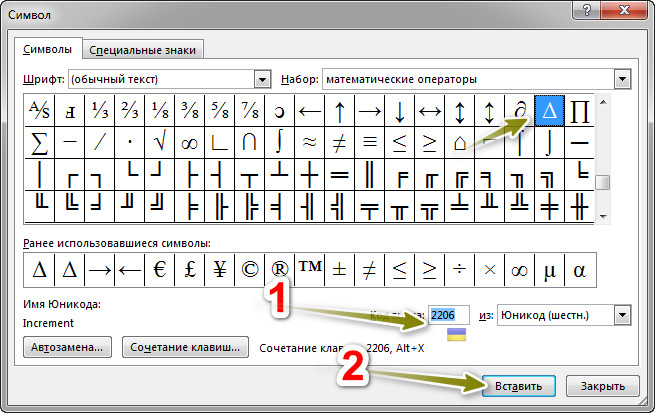
Но чтобы ускорить данный процесс (иногда приходится вводить одни и те же символы довольно часто) нужно ввести 2206 и не ставя пробела, нажать на клавиши Altl+X. Цифры автоматически преобразуются в треугольник.

Для такого символа можно добавить собственные сочетания клавиш. Для этого открываем окно символов («Вставка → Символ → Другие символы»). Ищем наш треугольник (способом, который описан выше). Тогда нажимаем на кнопку «Сочетание клавиш. ».

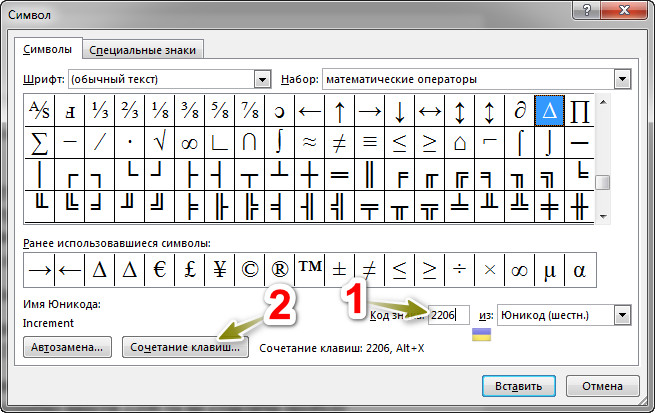
Вы увидите под текстом «Команды: » значок треугольника. Под текстом «Новое сочетание клавиш:» пишем клавиши, которые вам будет удобно использовать (я например, взял клавишу Ctrl и клавишу 1 на цифровой клавиатуре (клавиатура, которая находится сбоку и в некоторых моделях ноутбуков ее может не быть). Когда написали клавиши можно нажимать на кнопку «Назначить».

Теперь под текстом «Текущие сочетания:» будут клавиши, которые вы назначили. Окна после этого можно закрывать. Так как я назначил клавишу Ctrl и клавишу 1 на цифровой клавиатуре, то для вставки треугольника мне их нужно нажать.

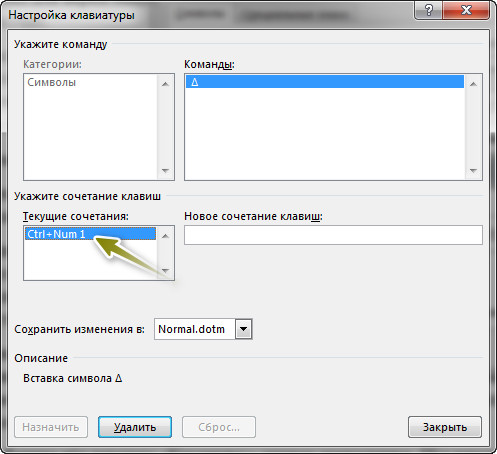
Многие пишут, что в роли треугольника можно вставить букву дельта. Для этого идем в «Вставка → Символ → Другие символы» и напротив текста «Код знака:» вводим в поле цифры 0394 и нажимаем «Вставить».

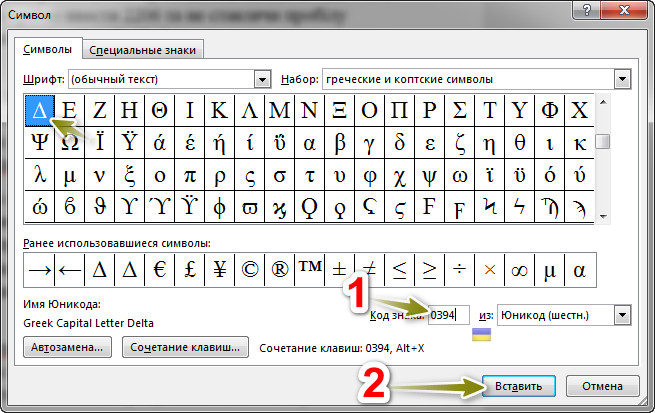
Для быстрого ввода пишем в Ворде 0394 и нажимаем клавиши Altl+X.

Я разницы между треугольниками, которые были добавлены двумя способами не увидел.

Доброго времени суток всем читающим! На связи Федор Лыков! Рад снова видеть вас и хотел сегодня бы поднять достаточно популярный для многих вопрос: как сделать табуляцию в ворде.

Вопрос, с одной стороны, может показаться достаточно тяжелым. Все дело в том, что многие просто не знают о том, что же такое эта «табуляция», а так же, как ее настраивать.

Сегодня, как и всегда попытаемся выяснить назначение этого параметра документа и его настройку. Желаю вам приятного чтения!

Цель и назначение использования

Символ табуляции – это, грубо говоря, пробел с настраиваемой длиной. Для добавления этого самого символа, необходимо нажать на клавиатуре клавишу «Tab» и тогда программа добавит этот самый проблем к позиции следующей. Правильно настроенные параметры позволит выровнять колонки, создать нужные отступы конкретных строк абзацев.

Так же она часто используется для того, чтобы отобразить данные в формате таблиц. Символы табуляции помогают в выравнивании столбцов и задании отступов. Настройку параметров можно производить как для отдельного абзаца, так и для всего текста в документе.

Изначально интервал данного символа — это пол дюйма или 1,25 см. Именно такое расстояние будет по стандарту при нажатии клавиши «Tab».

Позиция табуляции – символ на горизонтальной линейке над страницей. Она показывает длину отступа текста или место, с которого будет начинаться колонка текста

Давайте теперь разберемся, как устанавливать эти самые позиции.

Выбор типа табуляции и размещение с помощью линейки

Самым простым способом добавления и выбора типа является самая обычная работа с линейкой над страницей. Она идентично работает в ворде 2003 версии и в более современных (2007, 2010, 2013), а значит поэтому мы будем рассматривать пример на одной версии, так как различия отсутствуют.

Единственным отличием является отсутствие этой самой линейки по умолчанию в более современных версиях, но она достаточно легко и просто включается. Для этого необходимо:

Перейти на вкладку «Вид»
В блоке «отображение» поставить галочку «Линейка».

Как это должно выглядеть смотрите на скриншоте ниже.

После выполнения данного действия вы увидите привычную линейку над листом документа.

Наши дальнейшие действия

Теперь нам необходимо выбрать необходимый тип. Находятся они в самом вверху линейки, находящейся слева. Переключается тип однократным нажатием левой кнопки мыши.

Существует их несколько штук и давайте посмотрим немного подробнее на каждый из них.

Иконка	Название	Описание
	По левому краю	Текст будет выравниваться по левому краю страницы
	По центру	Текст будет выравниваться по центру
	По правому краю	Текст будет выравниваться по правому края страницы
	По разделителю	Выравнивает числа относительно десятичного разделителя. Не предназначен для текста. Чаще всего помогает при вводе таблиц с денежными суммами
	С чертой	Не выполняет выравнивание текста, а просто добавляет вертикальную черту в месте установки данного символа.

Итак, мы выбрали необходимый нам тип. Для добавления этого символа на наш документ, однократно щелкайте левой клавишей мышки в нижней части линейки в нужном месте листа. Если вы все сделали правильно, то увидите соответствующий значок на ней.

Теперь после нажатия «Tab» на клавиатуре наш мигающий текстовый курсор переместится в место нашего символа табуляции. С помощью той же левой кнопки мыши можно перетаскивать этот значок в любое место линейки. Если вы желаете удалить его, то просто сдвигайте его за пределы листа.

Это не единственный способ выставления символов. Линейка не дает такой точности и потому в некоторых ситуациях имеет смысл выставить значения вручную.

Делает это с помощью отдельного окна параметров, которое мы сейчас и рассмотрим.

Размещение с помощью окна параметров табуляции

С помощью данного окна выполняются более детальные настройки параметров, что иногда может потребоваться при форматировании текста. Так же, только в этом окне вы можете заполнить промежуток от одной табуляции до другой каким-либо символами чаще всего это делают с точками.

Итак, на 2003 версии офиса окно данных настроек вызывается следующим образом:

В верхней части окна программы левой кнопкой мыши нажимаем на всплывающее меню «Формат»
Из списка выбираем пункт «Табуляция», нажав на него левой клавишей мыши

На более современных версиях они вызываются несколько иначе:

Переходим на вкладку «Главная».
В модуле «Абзац» нажимаем маленькую стрелочку в нижнем правом углу.
В появившемся окне настроек абзаца выбираем снизу слева кнопку «Табуляция».

Перед нами откроется окно параметров, идентичное для обеих версий ворда, как для 2003, так и для более поздних.

В данном окошке мы сейчас и будем разбираться как сделать табуляцию в ворде.

Выглядят эти настройки вот так:

По порядку пробежимся по имеющимся опциям:

В данном окошечке мы пишем необходимую позицию в сантиметрах (например, 1 см) табуляции на странице.
В данном окне выставляется интервал стандартной табуляции. Как я и говорил в начале статьи, значение по умолчанию — это пол дюйма или 1,25 см.
Здесь требуется выбрать необходимый тип. Как помните, мы выше рассматривали каждый из них в таблице.
Выбор символов, которыми необходимо заполнить интервал от одной позиции табуляции до другой.

После установки требуемых параметров нажимайте на кнопку «Установить» и первая табуляция добавится в документ. Теперь можете устанавливать параметры для второго по аналогичному принципу.

Пример

Давайте рассмотрим небольшой пример и сделаем несколько табуляций, например на 1 см, 8 см и 15 см с типом по левому краю, по центру и по правому краю соответственно.

Как видите, значки стоят в необходимых местах, как мы и указали. Теперь предлагаю написать несколько слов для того, чтобы вы могли наглядно увидеть различие самых популярных типов и понять их работу.

Теперь хочу вам показать, как сделать табуляцию в ворде для содержания.

Как сделать правильное содержание

На данный момент мы с вами разобрались с некоторыми моментами. Полагаю, что кое-что для вас касательно данной темы уже должно было проясниться. Теперь я хочу показать вам пример того, как сделать табуляцию в ворде с точками.

Итак, как я и говорил, нам потребуется выполнить оглавление или содержание для примера.

Представим ситуацию, что мы пишем содержание для уже готового документа. Я написал «глава 1» и перешел по методу выше в окно настройки параметров «Табуляция». Нам необходимо в нем добавить одну с типом по правому краю и выбрать заполнитель под пунктом 2, а именно точки.

После установки параметров нажимаем «Установить» и «Ок». Обратите внимание на линейку и убедитесь, что значок табуляции установлен на необходимом вам значении. Если все на месте, то можно продолжать работать.

После слов «Глава 1» нажимаем «Tab» и видим необходимую нам картину.

Пишем любое число, которое может быть написано в подобном оглавлении. Для продолжения оглавления нажимаем «Enter», пишем вторую главу и снова нажимаем «Tab» и по нашим настройкам снова появится заполнение.

Очень просто, удобно и главное красиво. Достаточно актуально для школьников, студентов и просто людей, которые работают с электронными документами. Перейдем к заключению.

Заключение

Вот и подходит к концу наша статья по теме «Как сделать табуляцию в ворде». Надеюсь, что вам всё было понятно, интересно и главное полезно. Будет очень приятно, если данные знания, которые вы получили за данную публикацию действительно помогут вам в будущей работе с электронными документами.

Остались вопросы? Хотите поблагодарить? Спешите в комментарии. Я буду рад вашим вопросам, критике и благодарности. Обязательно на всё отвечу и с радостью помогу по компьютерной тематике.

Спасибо, что дочитали до конца! Встретимся в будущих статьях! Всего хорошего и до новых встреч!

Данную тематику я решил выбрать, потому что несколько дней назад, оформляя для вас очередную статью, я долго не мог понять, как добиться поставленной цели.

Если вставка десятичных вариантов не вызывает проблем, то обычные отношения одного числа к другому, записанные через черту вызывает много вопросов. Поэтому я решил структурировать информацию, чтобы подать её вам в понятной и главное — простой форме.

Как вы успели заметить, во всех моих статьях есть иллюстрации. Обычно я подготавливаю их на компьютере, но иногда приходится работать в полевых условиях. Поэтому приходится применять телефон, а чтобы переслать картинки с одного устройства на другое я использую Ватсап.

Ведь очень удобно сохранить их в галерею телефона и выполнить обработку на смартфоне.

Для решения основной задачи статьи есть несколько действенных методов. На данный момент у меня для вас есть четыре рабочих способа. Давайте перейдём к углублённому рассмотрению каждого из них.

Что нужно знать при использовании автозамены

Перед началом советую вам определиться, как должно выглядеть оформление в вашем документе: с горизонтальной или наклонной чертой. Ведь не каждый вариант действий подойдёт в той или иной ситуации. Однако спешу вас успокоить, что для каждого можно подобрать свою последовательность действий.

Например, чтобы получить дробь с наклонной чертой можно воспользоваться функцией автозамены.

После установки программы Word она заложена по умолчанию. Таким образом, когда вы прописываете два числа и между ними ставите знак «/». При этом не нужно использовать пробелы.

Я опробовал данный способ при вставке дроби ½. Начинайте последовательно набирать на клавиатуре следующие символы:

Готовы увидеть результаты своих трудов? Нажимайте пробел. После этого комбинация символов автоматически преобразуется в ½.

Однако стоит отметить, что данное правило применимо только для правильных отношений: ¼, ½, ¾. А вот что касается вариантов 9/2 или 7/3 преобразование не будет выполнено.

Если вы столкнулись с ситуацией, когда и правильные дроби не хотят превращаться, то стоит проверить, а включена ли функция автозамены.

Это делается следующим образом:

После открытия программы вам необходимо будет перейти во вкладку «Параметры».

Дальше вам нужно будет кликнуть по третьей строке сверху, которая носит название «Правописание».

Когда это будет выполнено, нам необходимо переключиться в раздел «Параметры автозамены».

В результате будет открыто новое окно.
В нём вы должны переключиться во вкладку «Автоформат при вводе».

Теперь нам нужно проверить наличие галочки – маркера напротив строки «дроби (½) соответствующими знаками».

Если квадрат пустой, то кликаем по нему левой кнопкой мыши и жмем кнопку «Ок».

Как в Ворде сделать дробь 2010 версия программы: используем спецсимволы

Есть ещё один способ, которым я частенько пользуюсь.

В нём описывалась последовательность действий через стандартную функцию «Вставка спецсимвола».

Чтобы попасть в неё, необходимо сделать следующее:

Первым действием открываем вкладку «Вставка», которую можно найти в верхнем меню программы.

Следующим шагом необходимо найти среди стандартных кнопок «Символ».

Если нажать на неё, то откроется диалоговое окно с часто используемыми символами. Если вы заинтересовались сегодняшней статьёй, то думаю, что дробей вы там не найдёте. Поэтому необходимо открыть полный список символов.

После этого нужно найти в списке интересующие нас дроби.

Завершением процесса будет двойной клик по квадратику с дробью или выбрать его и нажать кнопку «Вставить».

Покажу вам результат на примере дроби 1/3. Результат будет выглядеть, так как показано на изображении ниже.

Лично мне данный способ не очень нравится, так как перечень дробей катастрофически мал. К тому же расширить их невозможно. К тому же необходимо сделать много действий, чтобы получить положительный результат.

Как в Ворде сделать дробь: применение формул тестового редактора Word

Данный способ помогает сделать дробь с горизонтальным разделителем. Программой допускается вставка не только готовой формулы, но и создание дроби самостоятельно в редакторе.

Мой любимый мессенджер для общения это Ватсап. Для работы я применяю группы, в которые можно добавить нескольких адресатов. А спорные вопросы мы решаем с помощью создания опросов. Решение применяется на основе большинства проголосовавших.

Рассмотрим пример как в Ворде сделать дробь с горизонтальной чертой между числителем и знаменателем:

Заходим в раздел «Вставка» в верхней части документа.

Следующим действием необходимо кликнуть по строке «Вставить новую формулу».

После этого на экране появится поле, в котором можно собрать любую формулу, с помощью появившегося сверху конструктора. Именно в нём специально для вас придумана кнопка «Дробь».

Если нажать на эту кнопку, то появится перечень всевозможных шаблонов. Я покажу вам, например, как будет выглядеть результат вставки дроби с горизонтальной чертой.

Как мне кажется это самый простой и красивый вариант работы с дробями. Именно им я чаще всего и пользуюсь. Однако стоит отметить, что если нужно записать простую дробь, то лучше пользоваться первыми двумя способами.

Заключение

Вот и всё что мне хотелось бы вам рассказать в рамках статьи как в Ворде сделать дробь. Главное, чтобы моя информация помогла вам. Стоит отметить, что всё вышеперечисленное проверено мной на практике, поэтому можете смело опираться на неё в своей работе.

Выполнив все вышеперечисленные рекомендации в полном объёме, вы сможете вставить различные виды дроби. Для этого придуманы функции автозаполнение, вставка символов и формул. Разобравшись один раз с технологией, в дальнейшем можно будет легко пользоваться дробями при создании текстовых документов.

Читайте также: