Как сделать интерполяцию в автокаде
Собственно, есть проблема, имеются точки, хочется получить намного больше точек, исходя из информации об же существующих, т.е. проинтерполировать новые точки.
Я знаю один способ, но он очень извращенный, так что интересно, кто сталкивался с подобными проблемами, что и как делать подскажите? Как интерполируете точки вы.
По поводу програмного обеспечения, если честно не имею представления в каком софте (кроме аркгиса) можно это осуществить, однако предлагайте любые варианты (интересно, может lisp какой есть для када).
Заранее благодарю за помощь!
В программных продуктах AutoCAD Civil 3D и GeoniCS есть функции интерполяции и экстраполяции точек внутри и за пределами триангуляционной сети.
Особенностями этой процедуры является то, что результатом является некоторая точка имеющая координаты X, Y и Z соответствующие сумме значений координат всех вершин грани и деленное на количество вершин этой грани. То есть никаких сверхестественных расчетов не выполняется.
Алгоритм получения новых точек посредством процедур интерполяции и экстраполяции я видел в книге "Алгоритмы и структуры данных ГИС".
А расскажите ка про AutoCAD Civil 3D поподробнее, имею данную программу, даже больше скажу в ней работаю я, так вот хотелось бы узнать, как там интерполяция делается??В данный момент не имею установленного AutoCAD Civil 3D на компьютере, поэтому мне будет немного сложновато.
Зато на память могу сказать, как это делается в GeoniCS:
1. Изначально необходимо создать новую поверхность на базе имеющихся данных (данными является загруженная база геоточек).
2. Сделать эту поверхность текущей.
3. В меню "Геоточки" выбрать подменю "Редактирование геоточек", а затем "Интерполировать. " или "Экстраполировать".
4. И, наконец, указать координаты геоточки на экране в пределах триангуляционной сети или за ее пределами.
GeoniCS является аналогом AutoCAD Civil 3D, поэтому функцию интерполяции Вы сможете найти в меню "Points" или "Точки" (если AutoCAD Civil 3D русифицирован).
Спасибо, сейчас буду пробовать, а экстерполяция что такое есть? Репутация: 6 Откуда: москва Контактная информация: WeMaN, экстра- и интерполяция функции не ГИС и даже не софта, а математики. Советую прочитать что-нибудь общее про это, а то нахватаетесь конкретики раньше времени. Например, вот неплохие тексты. Последний раз редактировалось geologic 07 июл 2009, 15:15, всего редактировалось 1 раз. Экстраполяция - это определение высотного и/или планового положения некоторой точки за пределами поверхности.geologic Спасибо за совет, но как вы могли убедиться из текста выше, мне не столько нужна теория, сколько нужны способы того, как это можно сделать!! Ибо возникла задача интерполировать отметки!! Вот я и ищу методы
JEY У меня получилось создать интерполированную поверхность в Цивиле! Прикольно всё, только вот теперь задача как вершины треугольников превратить в точки с 3мя координатами?!
Репутация: 6 Откуда: москва Контактная информация: Если конкретно про модели местности, то вот.Но это уже ГИС, а вас как я понял, крупный масштаб интересует, т.е. инженерка. Не буду мешать А из каких объектов Вы создавали поверхность? По всем правилам AutoCAD Civil 3D, чтобы построить поверхность, нужно добавить группу точек в подразделе "Данные TIN" раздела "Поверхности".
geologic Почему именно инженерка? Вообще то у меня ГИС как таковой, но только на основе инженерки
Статью эту читал давно, нечто подобное я делал ещё в университете, однако из статьи почерпнул о возможности накладывать спутниковый снимок, получилось прикольно Но мы отвлеклись, при чём тут интерполяция?
JEY Не понимаю зачем вам такие подробности? Просто по точкам в Цивиле сделал поверхность, потом с ней произвёл интерполяцию и получилось что вместо сетки треугольников через 20 метров, у меня стала модель через метр, т.е. точки с интерполировались, теперь остаётся вопрос как треугольники преобразовать в точки.
Просто я не понимаю, зачем снова преобразовывать 3D-грани в точки. Достаточно открыть диалоговое окно списка точек, выделить все и добавить в чертеж одной командой из контекстного меню. Разве не это нужно? Ладно буду подробен, наверное не так выражаюсь.У меня есть набор точек с координатой z точки расположены друг от друга с шагом, допустим через 10 метров, мне надо с помощью интерполяции получиться дополнительно ещё точки, на основе уже существующих, но имующих шаг 10 м, т.е. из 10 метрового расстояния между точками получить точки с 1 метровым расстоянием. Мне нужный именно точки!
Что я для это делаю, я строю по своим точкам (которые с шагом 10 м) проверхность в Civile, получается треангуляционная сеть с шагом вершин треугольника через 10 м, ибо каждая вершина это точка по которой построена поверхность, с помощью меню интерполяции я преобразую поверхность с треугольниками в поверхность в которой вершинины треугольников идут через 1 метр, т.е. истинными являются вершины которые через 10 метров, а остальные вершины синтерполированны. Теперь мне нужно из этой поверхности получить вместо вершин треугольников точки с координатой z, которые соответсвуют всем вершинам интерполированной поверхности.
Понятно?
Вот теперь предельно понятно! Скажу сразу. Преобразовать 3D-грани в точки Вы не сможете. В AutoCAD Civil 3D такой команды нет. Я уже сталкивался с таким вопросом. Но тогда поверхность была построена посредством GeoniCS, что в принципе идентично Civil 3D.
Интерполяция была выполнена посредством добавления новых точек в режиме редактирования поверхности. То есть, в момент добавления новой точки поверхность автоматически перестраивалась в определенном участке, вместе с тем в список точек, каждый раз, добавлялась новая точка.
К чему веду? Полученные посредством интерполяции точки, были автоматически сохранены в проекте AutoCAD Civil 3D и Вы можете обнаружить их в списке точек. То есть не обязательно разбивать 3D-грани на составляющие!
Попробуйте внимательно проверить список точек. Скорее всего, результаты интерполяции Вы найдете там.

Как построить график по n точкам? Самое простое — отметить их маркерами на координатной сетке. Однако для наглядности их хочется соединить, чтобы получить легко читаемую линию. Соединять точки проще всего отрезками прямых. Но график-ломаная читается довольно тяжело: взгляд цепляется за углы, а не скользит вдоль линии. Да и выглядят изломы не очень красиво. Получается, что кроме ломаных нужно уметь строить и кривые. Однако тут нужно быть осторожным, чтобы не получилось вот такого:
Немного матчасти

Восстановление промежуточных значений функции, которая в данном случае задана таблично в виде точек P1 .  Pn, называется интерполяцией. Есть множество способов интерполяции, но все они могут быть сведены к тому, что надо найти n – 1 функцию для расчёта промежуточных точек на соответствующих сегментах. При этом заданные точки обязательно должны быть вычислимы через соответствующие функции. На основе этого и может быть построен график:
Функции fi могут быть самыми разными, но чаще всего используют полиномы некоторой степени. В этом случае итоговая интерполирующая функция (кусочно заданная на промежутках, ограниченных точками Pi) называется сплайном.
В разных инструментах для построения графиков — редакторах и библиотеках — задача «красивой интерполяции» решена по-разному. В конце статьи будет небольшой обзор существующих вариантов. Почему в конце? Чтобы после ряда приведённых выкладок и размышлений можно было поугадывать, кто из «серьёзных ребят» какие методы использует.
Ставим опыты
Самый простой пример — линейная интерполяция, в которой используются полиномы первой степени, а в итоге получается ломаная, соединяющая заданные точки.
Давайте добавим немного конкретики. Вот набор точек (взяты почти с потолка):

Результат линейной интерполяции этих точек выглядит так:
Однако, как отмечалось выше, иногда хочется получить в итоге гладкую кривую.
Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При этом в математике гладкость имеет порядок, равный номеру последней непрерывной производной, и область, на которой эта непрерывность сохраняется. То есть, если функция имеет гладкость порядка 1 на отрезке [a; b], это означает, что на [a; b] она имеет непрерывную первую производную, а вот вторая производная уже терпит разрыв в каких-то точках.
У сплайна в контексте гладкости есть понятие дефекта. Дефект сплайна — это разность между его степенью и его гладкостью. Степень сплайна — это максимальная степень использованных в нём полиномов.
Важно отметить, что «опасными» точками у сплайна (в которых может нарушиться гладкость) являются как раз Pi, то есть точки сочленения сегментов, в которых происходит переход от одного полинома к другому. Все остальные точки «безопасны», ведь у полинома на области его определения нет проблем с непрерывностью производных.
Чтобы добиться гладкой интерполяции, нужно повысить степень полиномов и подобрать их коэффициенты так, чтобы в граничных точках сохранялась непрерывность производных.

Традиционно для решения такой задачи используют полиномы третьей степени и добиваются непрерывности первой и второй производной. То, что получается, называют кубическим сплайном дефекта 1. Вот как он выглядит для наших данных:
Кривая, действительно, гладкая. Но если предположить, что это график некоторого процесса или явления, который нужно показать заинтересованному лицу, то такой метод, скорее всего, не подходит. Проблема в ложных экстремумах. Появились они из-за слишком сильного искривления, которое было призвано обеспечить гладкость интерполяционной функции. Но зрителю такое поведение совсем не кстати, ведь он оказывается обманут относительно пиковых значений функции. А ради наглядной визуализации этих значений, собственно, всё и затевалось.
Так что надо искать другие решения.

Другое традиционное решение, кроме кубических сплайнов дефекта 1 — полиномы Лагранжа. Это полиномы степени n – 1, принимающие заданные значения в заданных точках. То есть членения на сегменты здесь не происходит, вся последовательность описывается одним полиномом.
Но вот что получается:
Гладкость, конечно, присутствует, но наглядность пострадала так сильно, что… пожалуй, стоит поискать другие методы. На некоторых наборах данных результат выходит нормальный, но в общем случае ошибка относительно линейной интерполяции (и, соответственно, ложные экстремумы) может получаться слишком большой — из-за того, что тут всего один полином на все сегменты.
В компьютерной графике очень широко применяются кривые Безье, представленные полиномами k-й степени.
Они не являются интерполирующими, так как из k + 1 точек, участвующих в построении, итоговая кривая проходит лишь через первую и последнюю. Остальные k – 1 точек играют роль своего рода «гравитационных центров», притягивающих к себе кривую.
Вот пример кубической кривой Безье:

Как это можно использовать для интерполяции? На основе этих кривых тоже можно построить сплайн. То есть на каждом сегменте сплайна будет своя кривая Безье k-й степени (кстати, k = 1 даёт линейную интерполяцию). И вопрос только в том, какое k взять и как найти k – 1 промежуточную точку.
Здесь бесконечно много вариантов (поскольку k ничем не ограничено), однако мы рассмотрим классический: k = 3.
Чтобы итоговая кривая была гладкой, нужно добиться дефекта 1 для составляемого сплайна, то есть сохранения непрерывности первой и второй производных в точках сочленения сегментов (Pi), как это делается в классическом варианте кубического сплайна.
Решение этой задачи подробно (с исходным кодом) рассмотрено здесь.
Вот что получится на нашем тестовом наборе:
Стало лучше: ложные экстремумы всё ещё есть, но хотя бы не так сильно отличаются от реальных.
Думаем и экспериментируем

Можно попробовать ослабить условие гладкости: потребовать дефект 2, а не 1, то есть сохранить непрерывность одной только первой производной.
Достаточное условие достижения дефекта 2 в том, что промежуточные контрольные точки кубической кривой Безье, смежные с заданной точкой интерполируемой последовательности, лежат с этой точкой на одной прямой и на одинаковом расстоянии:
В качестве прямых, на которых лежат точки Ci – 1 (2) , Pi и Ci (1) , целесообразно взять касательные к графику интерполируемой функции в точках Pi. Это гарантирует отсутствие ложных экстремумов, так как кривая Безье оказывается ограниченной ломаной, построенной на её контрольных точках (если эта ломаная не имеет самопересечений).
Методом проб и ошибок эвристика для расчёта расстояния от точки интерполируемой последовательности до промежуточной контрольной получилась такой:


Первая и последняя промежуточные контрольные точки равны первой и последней точке графика соответственно (точки C1 (1) и Cn – 1 (2) совпадают с точками P1 и Pn соответственно).
В этом случае получается вот такая кривая:
Как видно, ложных экстремумов уже нет. Однако если сравнивать с линейной интерполяцией, местами ошибка очень большая. Можно сделать её ещё меньше, но тут в ход пойдут ещё более хитрые эвристики.

К текущему варианту мы пришли, уменьшив гладкость на один порядок. Можно сделать это ещё раз: пусть сплайн будет иметь дефект 3. По факту, тем самым формально функция не будет гладкой вообще: даже первая производная может терпеть разрывы. Но если рвать её аккуратно, визуально ничего страшного не произойдёт.
Отказываемся от требования равенства расстояний от точки Pi до точек Ci – 1 (2) и Ci (1) , но при этом сохраняем их все лежащими на одной прямой:
Эвристика для вычисления расстояний будет такой:
При этом, однако, стоит ещё проверять, не совпали ли точки Pi и Pi + 1 по ординате, и, если совпали, полагать l1 = l2 = 0. Это защитит от «вспухания» графика на плоских отрезках (что тоже немаловажно с точки зрения правдивого отображения данных).

Результат получается такой:

Результат следующий:
На этом было принято решение признать цель достигнутой.
Может быть, кому-то пригодится код.
А как люди-то делают?
Обещанный обзор. Конечно, перед решением задачи мы посмотрели, кто чем может похвастаться, а уже потом начали разбираться, как сделать самим и по возможности лучше. Но вот как только сделали, не без удовольствия ещё раз прошлись по доступным инструментам и сравнили их результаты с плодами наших экспериментов. Итак, поехали.
MS Excel

Это очень похоже на рассмотренный выше сплайн дефекта 1, основанный на кривых Безье. Правда, в отличие от него в чистом виде, тут всего два ложных экстремума — первый и второй сегменты (у нас было четыре). Видимо, к классическому поиску промежуточных контрольных точек тут добавляются ещё какие-то эвристики. Но ото всех ложных экстремумов они не спасли.
LibreOffice Calc

В настройках это названо кубическим сплайном. Очевидно, он тоже основан на Безье, и вот тут уже точная копия нашего результата: все четыре ложных экстремума на месте.

Есть там ещё один тип интерполяции, который мы тут не рассматривали: B-сплайн. Но для нашей задачи он явно не подходит, так как даёт вот такой результат :)
Highcharts, одна из самых популярных JS-библиотек для построения диаграмм

Тут налицо «метод касательных» в варианте равенства расстояний от точки интерполируемой последовательности до промежуточных контрольных. Ложных экстремумов нет, зато есть сравнительно большая ошибка относительно линейной интерполяции (седьмой сегмент).
amCharts, ещё одна популярная JS-библиотека

Картина очень похожа на экселевскую, те же два ложных экстремума в тех же местах.
Coreplot, самая популярная библиотека построения графиков для iOS и OS X

Есть ложные экстремумы и видно, что используется сплайн дефекта 1 на основе Безье.
Библиотека открытая, так что можно посмотреть в код и убедиться в этом.
aChartEngine, вроде как самая популярная библиотека построения графиков для Android

Больше всего похоже на кривую Безье степени n – 1, хотя в самой библиотеке график называется «cubic line». Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.

Доброго времени, Хабр!
Куча времени прошла с того момента, как я написал свою первую статью, и уже почти год с того момента, как пришла в голову идея для второй. В силу многих обстоятельств (в первую очередь – лени и забывчивости), эта идея так и не была реализована ранее, но сейчас я собрался, написал весь этот материал и готов представить его вашему вниманию.
Начну с небольшой вводной. Будучи студентом 4-го, на тот момент, курса бакалавриата, я изучал курс «Компьютерная графика». Много там было разных интересных (и не очень) заданий, но одно прямо особо запало мне в душу: интерполяция кубическими сплайнами с заданными первыми производными на концах интервала. Пользователь должен был задавать значения первых производных, а программа — считать и выводить на экран интерполяционную кривую. Особенность и основная сложность задания заключена в том, что задаются именно первые производные, а не вторые, как в классической постановке сплайн-интерполяции.
Как я ее решал, и к чему оно в итоге пришло, я как раз и изложу в этой статье. И да, если по описанию задачи вы не поняли ни в чем ее смысл, ни в чем сложность, не переживайте, все это я также постараюсь раскрыть. Итак, поехали.
А, нет, погодите один момент. Вот вам два числовых ряда:
a) 2, 4, 6, 8, ?
b) 1, 3, ?, 7, 9
Какие числа должны стоять на месте вопросов и почему? Вы действительно уверены в своем ответе?
Интерполяция
Интерполяция, интерполирование (от лат. inter-polis – «разглаженный, подновлённый, обновлённый; преобразованный») – в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. (с) Википедия
Поясню на примерах. Существуют задачи, когда нам требуется узнать, условно, «закон распределения» (взял в кавычки, так как это, вообще говоря, термин из другой области математики) некого параметра по нескольким известным его значениям. Чаще всего речь идет об изменении некого параметра во времени: координаты движущегося тела, температуры объекта, колебания курса валюты, etc. При этом в силу каких-либо обстоятельств у нас не было возможности наблюдать за этим параметром непрерывно, мы могли узнавать его значения лишь в какие-то отдельные моменты времени. Исходными данными в таком случае у нас является множество точек вида value(time), а целью задачи – восстановить кривую, проходящую через эти точки и непрерывно описывающую изменение этого параметра.
Следует понимать, что невозможность постоянного наблюдения за соответствующим параметром – это обычно какого-либо рода технологическое ограничение. С развитием техники таких ситуаций становится все меньше и меньше. Из современных задач такого плана – траектория движения, например, марсохода. Поддерживать непрерывный сеанс связи (пока что) все еще не представляется возможным, а контролировать его перемещение и рисовать красивые траектории хочется. Получается, что конкретные координаты можно узнать только в те моменты, когда связь все-таки налажена, а траекторию целиком приходится восстанавливать по полученным таким образом время от времени точкам.
Другой вариант применения интерполяции. Некоторые современные телевизоры показывают изображение с частотой обновления картинки до >=1000Гц (хотя это все еще запредельные значения). Большинство телевизоров так не умеет, но даже так многие отображают картинку на частоте 100Гц — такая величина уже вполне себе классика. А если верить википедии, то в кинематографе «частота 24 кадра в секунду является общемировым стандартом». Для того, чтобы превратить 24 кадра в секунду исходного видеопотока в 100 кадров в секунду результата, телевизор использует интерполяцию. А именно какие-нибудь алгоритмы в стиле «взять два соседних кадра 1 и 2, посчитать разницу между ними и сформировать из нее 3 дополнительных кадра, которые надо впихнуть между теми двумя изначальными» -> получаются кадры 1, 1_1, 1_2, 1_3, 2
Для дальнейших рассуждений возьмем более простой пример. Представим себе, например, лабораторную работу по географии в каком-нибудь 6-ом классе (кстати, у меня когда-то и правда была такая). Необходимо каждые 3 часа измерять температуру воздуха и записывать данные, а потом сдать учителю график изменения температуры от времени суток. Допустим, по результатам измерений у нас получилась вот такая табличка (данные придуманы случайным образом и никак не претендуют на какую-либо правдоподобность):
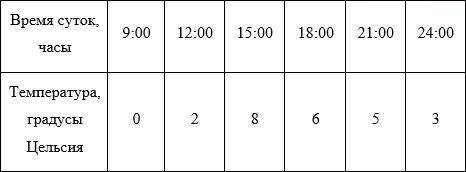
Отобразим полученные данные на графике:
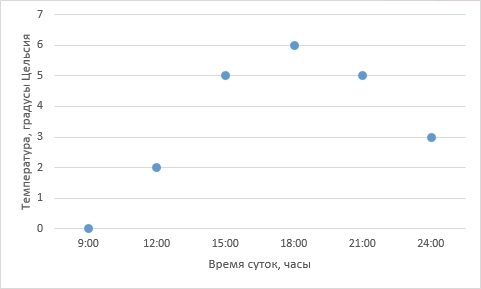
Собственно, данные записаны и отражены на графике. Мы вплотную подошли к задаче интерполяции – как по имеющимся точкам восстановить плавную кривую?
Количество условий и степень интерполирующего полинома
Можем ли мы вообще гарантировать, что такая функция, которая соединяет все заданные точки, вообще существует?
Да, такая функция гарантированно существует, и более того, таких функций будет бесконечно много. Для любого набора точек можно будет придумать сколько угодно много функций, которые через них будут проходить. И вот несколько примеров того, как две точки можно соединить разными способами:
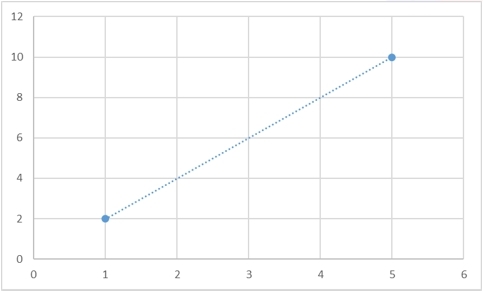
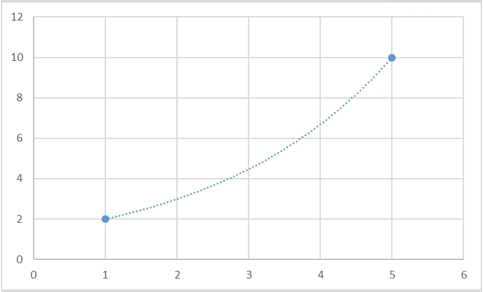

Однако есть и способ задать интерполяционную кривую однозначно. В самом классическом случае, в качестве интерполяционной кривой берут полином:
Для того, чтобы провести через имеющиеся точки такой полином единственным образом, необходимо и достаточно, чтобы степень полинома была на 1 меньше, чем количество условий (я специально выделил это слово, потому что в конце этого раздела я вернусь к этой формулировке). Пока что, простоты ради, условием будут являться координаты точки. Говоря человеческим языком, через 2 точки однозначным образом можно провести прямую (полином 1-ой степени), через 3 точки – параболу (полином 2-ой степени) и т.д.
Возвращаясь к нашей задаче с температурой – в ней мы определили 6 точек, значит, для того, чтобы провести полином единственным образом, он должен быть 5-ой степени

Интерполирующий полином тогда будет выглядеть так:
А сейчас следует сделать важное замечание и пояснить, что я имел ввиду под «условием». Полином можно задать не только координатами точек, через которые он проходит, условиями могут быть любые параметры этого полинома. В простейшем случае это действительно координаты точек. Но в качестве условия можно взять, например, первую производную этого полинома в какой-либо из точек. Вторую производную. Третью производную. В общем, любую возможную производную в любой из точек, в которой этот полином существует. Поясню на примере:
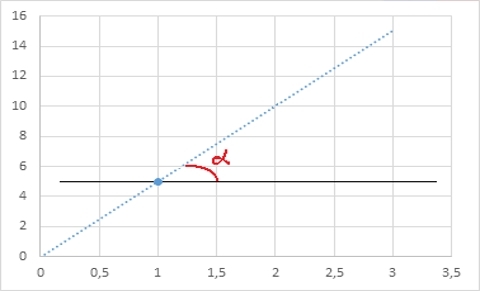
Прямую можно задать однозначно, как я уже говорил, двумя точками:

Ту же прямую, с другой стороны, можно определить координатой одной точки и углом наклона альфа к горизонтали:
С полиномами более высоких степеней можно использовать и более сложные условия (вторая производная, третья производная, etc.), и каждый такой параметр будет идти в общий счет количества условий, которые однозначным образом определят этот полином. Чтобы не быть голословным, вот еще пример:
Пусть нам заданы такие три условия:
Условий три, значит, мы хотим получить полином второй степени:
Считаем первую производную и считаем
Считаем вторую производную и считаем
Отсюда получаем, что наш полином выглядит так:
Интерполяция кубическими сплайнами
Вот, по тиху, мы и подбираемся к моей задаче. Полиномиальная интерполяция – не единственно возможный способ интерполяции. Среди всех прочих методов существует метод интерполяции кубическими сплайнами.
Принципиальное отличие идеи сплайн-интерполяции от интерполяции полиномом состоит в том, что полином один, а сплайн состоит из нескольких полиномов, а именно их количество равно количеству инервалов, внутри которых мы производим интерполяцию. В примере с нашей температурой воздуха, в которой у нас определено 6 точек, у нас будет 5 интервалов – соответственно, у нас будут 5 полиномов, каждый на своем интервале.
Каждый из этих полиномов – это полином третьей степени (строго говоря, степени не выше третьей, так как на каком-то из интервалов интерполирующая кривая может становиться квадратичной параболой или даже линейной функцией, но в общем случае это все-таки полином именно третьей степени). Записывая вышесказанное формульно, получим что все наши точки будут соединены некоей кривой , где каждый – это полином третьей степени, а именно:
Возвращаясь к рассказанному в предыдущем пункте, для того, чтобы однозначно задать один полином 3-ей степени, необходимо 4 условия. В этой задаче у нас 5 полиномов, то есть, чтобы задать их все, нам нужно суммарно 5∙4=20 условий. И вот как они получаются:
1) Первый полином определен на первой и второй точках – это два условия. Второй полином определен на второй и третьей точках – еще два условия. Третий полином, четвертый, пятый – каждый из них определен на 2-х точках – суммарно это дает 10 условий.
2) Для каждой промежуточной точки из множества (а это 4 точки с временами 12:00, 15:00, 18:00, 21:00) должно выполняться условие, что первые и вторые производные для левого и правого полиномов должны совпадать. Формульно:
По два таких условия на каждую из промежуточных точек дает еще 8 условий. Следует добавить, что мы задаем только сам факт равенства, а какое конкретно значение они при этом принимают – это совершенно иная задача и считается она довольно сложно.
3) Остаются два условия, которые пока еще не определены. Это так называемые «граничные условия», от задания которых и зависит, какой именно сплайн получится. Обычно задают вторые производные на концах интервала равными 0:
Если сделать так, то мы получим так называемый «естественный сплайн». Для вычисления таких сплайнов написано уже огромное количество библиотек, бери и используй любую.
Отличие моего задания от классической постановки задачи, мои размышления над заданием и само решение
И вот мы подошли к условию моей задачи. Преподаватель придумал такое задание, что задаваться должны первые производные и на левом и правом концах интервала, а программа должна считать интерполирующую кривую. А для такого требования готовых алгоритмов я не нашел…
Я, разумеется, не стану описывать весь твой «творческий» путь от момента, когда я услышал задание, до того, как я его сдал. Расскажу лишь саму идею и покажу ее реализацию.
Для того, чтобы однозначно задать кубический полином на этом интервале, нам не хватает еще лишь одного условия. Но мы можем его просто придумать! Возьмем вторую производную и положим ее равной, например, 0:
— ничем не обоснованное предположение
Таким образом, зная эти 4 условия, мы полностью определяем этот полином. Зная все параметры этого полинома, мы можем вычислить значения первой и второй производных на второй точке, и поскольку они совпадают со значениями первой и второй производной для полинома на втором интервале, это приводит к тому, что мы также определяем и второй полином:
Аналогично мы считаем третий полином, четвертый, пятый и так далее, сколько бы их ни было. То есть, по факту, воссоздаем весь сплайн. Но поскольку мы взяли совершенно случайным образом, это приведет к тому, что производная , заданная пользователем на правом конце сплайна, не будет совпадать с производной , которая получилась у нас в ходе таких вычислений. Но получается, что значение производной на правом конце сплайна – это функция, зависящая от значения второй производной на левом конце:
А поскольку такой сплайн, который бы удовлетворял заданным условиям, гарантированно существует, и существует в единственном экземпляре, это значит, что мы можем рассмотреть разность:
и попытаться найти такое значение , при котором обращалась бы в 0 – и это будет тем самым правильным значением , которое строит искомый пользователем сплайн:
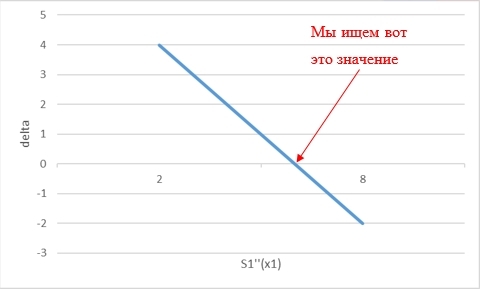
Самое замечательное в моей идее то, что эта зависимость оказалась линейной (вне зависимости от количества точек, через которые мы проводим сплайн. Этот факт доказан теоретическими подсчетами), а значит можно случайным образом взять любые два начальные значения и , посчитать и , и сразу же посчитать то самое верное значение, которое построит нам искомый сплайн:
Итого, мы гарантированно находим искомый сплайн за 3 прогонки таких вычислений.
Немного кода и скриншотов программы
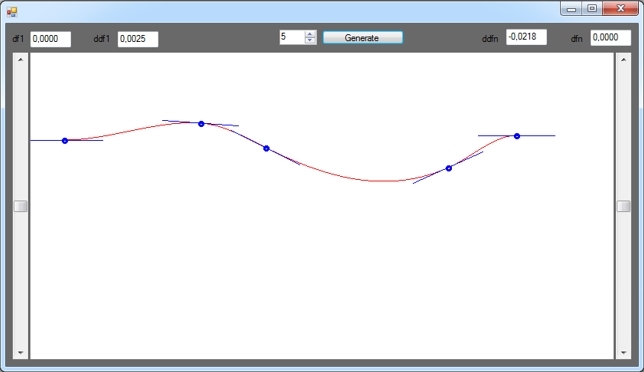


Синие отрезки — это первые производные сплайна в соответствующих его точках. Добавил такой вот графический элемент для большей наглядности.
Достоинства и недостатки алгоритма
Признаюсь честно, я не проводил сколь-либо серьезного анализа. По-хорошему стоило бы написать тесты, проверить, как оно работает в разных условиях (мало/много точек интерполяции, равное/произвольное между точками, линейные/квадратные/кубические/тригонометрические/etc. функции и так далее), но я этого не сделал, простите :)
Навскидку можно сказать, что сложность алгоритма — O(N), так как, как я уже говорил, вне зависимости от количества точек, достаточно двух прогонов вычислений, чтобы получить правильное значение второй производной на левом конце интервала, и еще одного, чтобы построить сплайн.
Впрочем, если кому-то захочется покопаться в коде и провести какой-нибудь более подробный анализ этого алгоритма, я буду только рад. Напишите мне разве что о результатах, мне было бы интересно.
Так а в чем провинились тесты IQ?
В самом начале статьи я написал два числовых ряда и попросил их продолжить. Это довольно частый вопрос во всяких IQ тестах. В принципе, вопрос как вопрос, но если копнуть чуть глубже, окажется, что он довольно бредовый, потому что при некотором желании можно доказать, что «правильного» ответа на него не имеется.
Рассмотрим для начала ряд «2, 4, 6, 8, ?»
Представим себе этот числовой ряд как множество пар значений :

, где в качестве мы берем само число, а в качестве – порядковый номер этого числа. Какое значение должно быть на месте ?
Мысль, к которой я стараюсь плавно подвести – это то, что мы можем подставить абсолютно любое значение. Ведь что по факту проверяют такие задачи? Способность человека найти некое правило, которое связывает все имеющиеся числа, и по этому правилу вывести следующее число в последовательности. Говоря научным языком, здесь стоит задача экстраполяции (задача интерполяции состоит в том, чтобы найти кривую, проходящую через все точки внутри некоторого интервала, а задача экстраполяции – продолжить эту кривую за пределы интервала, «предсказав» таким образом поведение кривой в дальнейшем). Так вот, экстраполяция не имеет однозначного решения. Вообще. Никогда. Если бы было иначе, люди давным-давно бы предсказали прогноз погоды на всю историю человечества вперед, а скачки курса рубля никогда не были бы неожиданностью.
Разумеется, предполагается, что верный ответ в этой задаче все-таки есть и он равен 10, и тогда «закон», связывающий все эти числа, – это
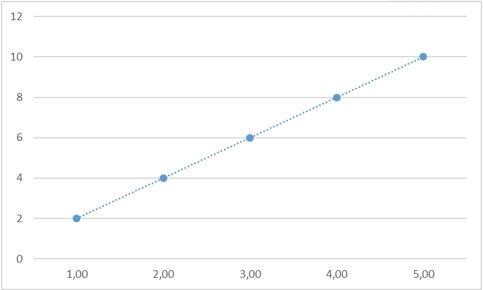
Однако возьмем любое другое значение – и мы также сможем найти закон, который бы обосновывал именно его:
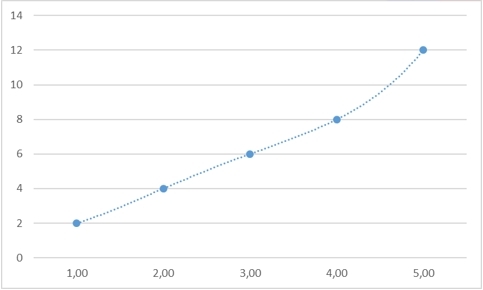
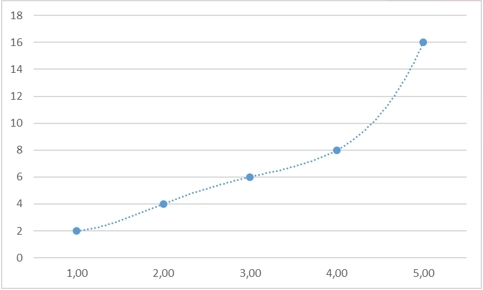
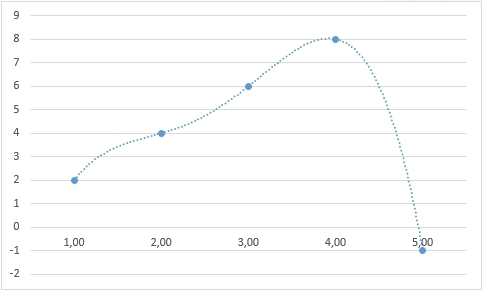
Хорошо, с экстраполяцией разобрались, она не имеет однозначного решения даже теоретически. Но, быть может, мы сможем найти пропущенное число во втором ряду?
Читайте также:


