Как построить годограф в excel

Построение диаграммы в Microsoft Excel по таблице – основной вариант создания графиков и диаграмм другого типа, поскольку изначально у пользователя имеется диапазон данных, который и нужно заключить в такой тип визуального представления.
В Excel составить диаграмму по таблице можно двумя разными методами, о чем я и хочу рассказать в этой статье.
Способ 1: Выбор таблицы для диаграммы

Откройте необходимую таблицу и выделите ее, зажав левую кнопку мыши и проведя до завершения.

Вы должны увидеть, что все ячейки помечены серым цветом, значит, можно переходить на вкладку «Вставка».

Там нас интересует блок «Диаграммы», в котором можно выбрать одну из диаграмм или перейти в окно с рекомендуемыми.

Откройте вкладку «Все диаграммы» и отыщите среди типов ту, которая устраивает вас.

Справа отображаются виды выбранного типа графика, а при наведении курсора появляется увеличенный размер диаграммы. Дважды кликните по ней, чтобы добавить в таблицу.

Предыдущие действия позволили вставить диаграмму в Excel, после чего ее можно переместить по листку или изменить размер.

Дважды нажмите по названию графика, чтобы изменить его, поскольку установленное по умолчанию значение подходит далеко не всегда.

Не забывайте о том, что дополнительные опции отображаются после клика правой кнопкой мыши по графику. Так вы можете изменить шрифт, добавить данные или вырезать объект из листа.

Для определенных типов графиков доступно изменение стилей, что отобразится на вкладке «Конструктор» сразу после добавления объекта в таблицу.
Как видно, нет ничего сложного в том, чтобы сделать диаграмму по таблице, заранее выбрав ее на листе. В этом случае важно, чтобы все значения были указаны правильно и выбранный тип графика отображался корректно. В остальном же никаких трудностей при построении возникнуть не должно.
Способ 2: Ручной ввод данных
Преимущество этого типа построения диаграммы в Экселе заключается в том, что благодаря выполненным действиям вы поймете, как можно в любой момент расширить график или перенести в него совершенно другую таблицу. Суть метода заключается в том, что сначала составляется произвольная диаграмма, а после в нее вводятся необходимые значения. Пригодится такой подход тогда, когда уже сейчас нужно составить график на листе, а таблица со временем расширится или вовсе изменит свой формат.

На листе выберите любую свободную ячейку, перейдите на вкладку «Вставка» и откройте окно со всеми диаграммами.

В нем отыщите подходящую так, как это было продемонстрировано в предыдущем методе, после чего вставьте на лист и нажмите правой кнопкой мыши в любом месте текущего значения.

Из появившегося контекстного меню выберите пункт «Выбрать данные».

Задайте диапазон данных для диаграммы, указав необходимую таблицу. Вы можете вручную заполнить формулу с ячейками или кликнуть по значку со стрелкой, чтобы выбрать значения на листе.

В блоках «Элементы легенды (ряды)» и «Подписи горизонтальной оси (категории)» вы самостоятельно решаете, какие столбы с данными будут отображаться и как они подписаны. При помощи находящихся там кнопок можно изменять содержимое, добавляя или удаляя ряды и категории.

Обратите внимание на то, что пока активно окно «Выбор источника данных», захватываемые значения таблицы подсвечены на листе пунктиром, что позволит не потеряться.

По завершении редактирования вы увидите готовую диаграмму, которую можно изменить точно таким же образом, как это было сделано ранее.
Вам остается только понять, как сделать диаграмму в Excel по таблице проще или удобнее конкретно в вашем случае. Два представленных метода подойдут в совершенно разных ситуациях и в любом случае окажутся полезными, если вы часто взаимодействуете с графиками во время составления электронных таблиц. Следуйте приведенным инструкциям, и все обязательно получится!

График функции – графическое представление математического выражения, показывающее его решение. Для построения обычно используются линейные графики с точками, с чем прекрасно справляется Microsoft Excel. Кроме того, в нем еще можно выполнить автоматические расчеты, быстро подставив нужные значения.
Существует огромное количество функций, поэтому в качестве примера я разберу только две самые наглядные, чтобы вы поняли базовые правила составления подобных элементов в таблице.
График функции F(x) = X^2
Функция X^2 – одна из самых популярных математических функций, которую разбирают еще на уроках в школе. На графике необходимо показать точки Y, что в Excel реализовывается следующим образом:

Создайте строку на листе в программе, вписав туда известные значения X.

Сделайте то же самое и с Y. Пока значения этой оси координат неизвестны. Чтобы определить их, нам нужно выполнить простые расчеты.

Поэтому в качестве значения для каждой ячейки укажите формулу, которая посчитает квадрат числа, указанного в строке X. Для этого впишите =A1^2, заменив номер ячейки.

Теперь достаточно зажать левую кнопку мыши на нижней точки готовой ячейки и растянуть таблицу, чтобы формула автоматически подставилась в остальные ячейки, и вы могли сразу ознакомиться с результатом.

Перейдите на вкладку вставки и выберите раздел с рекомендуемыми диаграммами.

В списке отыщите точечную диаграмму, которая подойдет для составления подходящего графика.

Вставьте ее в таблицу и ознакомьтесь с результатом. На следующем скриншоте вы видите параболу и значения X, при которых она получилась правильной (такую часто показывают в примерах на математике).
Всего 7 простых шагов потребовалось для достижения желаемого результата. Вы можете подставлять свои значения в таблицу и изменять их в любое время, следя за тем, как перестраивается график функций.
График функции y=sin(x)
y=sin(x) – вторая функция, которую мы возьмем за пример. Может показаться, что ее составление осуществляется сложнее, хотя на самом деле это не так. Дело в том, что Excel сам посчитает значения, а вам останется только задать известные числа и вставить простой линейный график для вывода результатов на экран.

Если вам будет проще, впишите в отдельную клетку функцию, укажите интервал и шаг. Так вы не запутаетесь при дальнейшем заполнении ячеек.

Добавьте два столбца, в которые будут вписаны значения каждой оси. Это нужно не только для обозначения чисел, но и для их вычисления при помощи функций программы.

Начните вписывать значения X с необходимым интервалом и шагом. Кстати, вы можете заполнить всего несколько полей, а затем растянуть клетки таким же образом, как было показано в предыдущем примере, чтобы они подставились автоматически до конца вашего интервала.

Теперь более сложное, но не страшное действие – определение значения Y. Понятно, что он равняется синусу X, значит, нужно вписать функцию =SIN(A1), где вместо A1 используйте нужную ячейку, а затем растяните функцию на оставшийся интервал.

На следующем скриншоте вы видите результат заполнения таблицы. Используйте округление для удаления лишних знаков после запятой.

Вставьте обычную линейчатую диаграмму и ознакомьтесь с результатом.
На примере этих двух функций уже можно понять, как работает построение графиков в Экселе. При использовании других функций просто учитывайте особенности заполнения ячеек и не забывайте о том, что вам не нужно ничего считать, поскольку Excel все сделает за вас после указания необходимой формулы.

(1)
где и полиномы комплексного переменного s, - некоторый параметр, который в дальнейшем будем называть варьируемым. (Таким параметром может служить, например, передаточный коэффициент k разомкнутой системы).
Имея характеристическое уравнение (1) с известными нулями входящих в него полиномов L(s) и D(s) можно приблизительно построить на плоскости S корневые годографы.
Для этого (1) переписываем в виде:

(2)
Учитывая, что s - комплексная переменная, (2) можно записать в виде двух уравнений: уравнения аргументов
и уравнения модулей

. (4)
Представим и в виде:

,

,
где и - коэффициент при s наивысшей степени,
, - нули полиномов и ,
m и n – порядки полиномов и .
Уравнение аргументов (3) можно переписать в следующем виде:
(Сказанное показано на рис.1)

На этом рисунке через обозначены аргументы векторов, проведенных из полюсов , аргумент вектора, проведенного из нуля .
На основании выражения (5) можно сформулировать следующие основные правила построения корневых годографов:
1. Вещественная ось плоскостей S является осью симметрии для корневых годографов и для асимптот корневых годографов.
Если число полюсов n больше числа нулей m, то (n-m) ветвей корневого годографа уйдут в бесконечность. Если число нулей больше числа полюсов, то (n-m) ветвей корневого годографа придут из бесконечности.
3. Ветви корневых годографов, находящихся в бесконечности имеют асимптоты. Число асимптот равно . Асимптоты пересекаются в одной точке вещественной оси плоскости S, причем:

, (6)

и имеют углы наклона относительно положительного направления вещественной оси плоскости S:

4. Точки вещественной оси плоскости S справа от которых находится нечетное число нулей и полюсов функции обязательно принадлежат корневым годографам, а точки этой оси справа от которых находится четное число нулей и полюсов не могут принадлежать корневым годографам.
5. В некоторых точках вещественной оси плоскости S, принадлежащих корневым годографам, корневые годографы могут, встретившись, разойтись, один в верхнюю, а другой в нижнюю части плоскости S.
Сформулированные выше правила позволяют приближенно выполнить построение корневых годографов.
Рассмотрим некоторые примеры построения корневых годографов.
Построить корневые годографы для варьируемого параметра К для замкнутой системы, если передаточная функция разомкнутой системы:

Пример 1.
Решение: Характеристическое уравнение замкнутой системы . Представим его в виде . Отсюда видно, что количество нулей равно 0, а количество полюсов равно 4. Их значения можно получить, найдя корни знаменателя. Получаем

Наносим полюса на комплексную плоскость. В соответствии с правилом 2 все корневые годографы должны уйти в бесконечность. Число асимптот равно 4-0=4. Определим точку, расположенную на вещественной оси, в которой пересекаются асимптоты –7,5
Определим углы, которые асимптоты составляют с положительным направлением вещественной оси (правило 3).


Наносим асимптоты на комплексную плоскость, как показано на рис.2. На этом же рисунке показаны корневые годографы, которые выходят из полюсов и уходят в бесконечность, неограниченно приближаясь к нарисованным асимптотам.

Рис.2


Решение: Характеристическое уравнение замкнутой системы имеет вид

Отсюда .
Приравнивая к нулю числитель и знаменатель, получим нули и полюса корневых годографов



Наносим полюса и нули на комплексную плоскость, как показано на рис.2. В соответствии с правилом 1, два корневых годографа должны закончиться в бесконечности, кроме того в соответствии с правилом 4 ни одна из точек вещественной плоскости не принадлежит корневым годографам.
В соответствии с правилом 3, корневые годографы имеют 2 асимптоты, пересекающиеся с вещественной осью в точке

Углы между асимптотами и положительным направлением вещественной оси будут равны (правило 3)

С учетом сказанного корневые годографы будут иметь вид, показанный на рис.3. Корневые годографы выйдя из полюсов P1 и P2 закончатся в нулях N1 и N2. Корневые годографы выйдя из полюсов P3 и P4 уйдут в бесконечность неограниченно приближаясь к асимптотам, пересекающим вещественную ось в точке –55.


Пример 3.
Решение: Характеристическое уравнение замкнутой системы

Представим его в виде

Нули корневых годографов будут:

Полюса корневых годографов будут:

Наносим нули и полюса на комплексную плоскость, как показано на рис. 4. В соответствии с правилом 4, часть вещественной оси, лежащая левее нуля N3 будет принадлежать корневым годографам, при этом этот отрезок оси является асимптотой для годографа, уходящего в бесконечность.
Корневые годографы, построенные в соответствии с изложенными выше правилами, изображены на том же рисунке. Два корневых годографа, выйдя из полюсов P1 и P2 придут в нули N1 и N2. Корневые годографы, выйдя из полюсов P3 и P4 сойдутся в одной точке на вещественной оси, равной примерно 84 и, затем один закончится нуле N3, а другой уйдет в бесконечность.
W (s) = ,
Построить годографы Михайлова и Найквиста. Определить частоту среза системы.
Определить критическое значение коэффициента усиления системы.
Решение.
А) Выписываем характеристический полином для замкнутой системы
A(s) = 50 + (30s+1) (0,4s+1)(0,01s+1) = 50+(900 +60s+1)(0,004 +0,41s+1) = 3,6 +369,24 +924,604 +60,41s+51.
В) Выделим действительную и мнимую часть.
A= U( )+jV( ), где U( ) – действительная часть, а V( ) – мнимая часть.
Г) Построим годограф Михайлова:
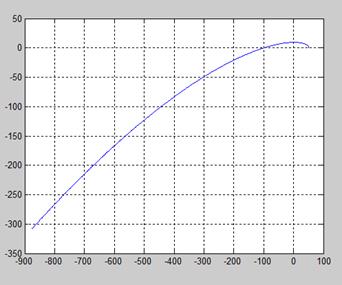
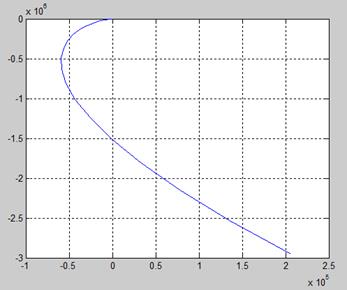
Д) Проверим устойчивость системы с помощью критерия Михайлова:
Из решения видно (см. рис.1 и рис.2), что годограф удовлетворяет всем условиям критерия:
W (s) = ,
Б) Раскроем скобки и выделим действительную и мнимую часть в знаменателе
W ( ) = ,
В) Умножим на сопряженное и выделим действительную и мнимую часть

,

где U( ) – действительная часть, а V( ) – мнимая часть.
Г) Построим годограф Найквиста:
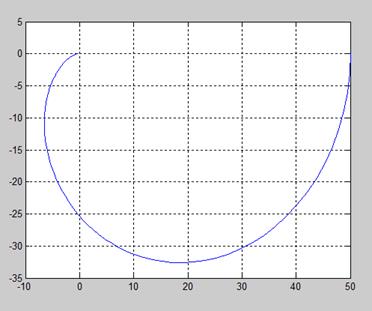
Рис.3. Годограф Найквиста.
Д) Проверим устойчивость системы с помощью критерия Найквиста:
Критерий Найквиста: Для того чтобы система, которая в разомкнутом состоянии была устойчива, была устойчива и в замкнутом, необходимо, чтобы годограф Найквиста при изменении частоты от нуля до бесконечности не охватывал точку с координатами (-1; j0).
Из решения видно (см. рис.3), что годограф удовлетворяет всем условиям критерия:
- Годограф меняет свое направление по часовой стрелке
- Годографом не охватывается точка (-1; j0)
- Делаем вывод, что данная разомкнутая система устойчива.
- Определение критического значения коэффициента усиления системы.
А) В пункте 2 уже были выделены действительная и мнимая части

Б) Для того, чтобы найти критическое значение коэффициента усиления системы необходимо приравнять мнимую часть к нулю, а действительную к -1

= -1 (1)

= 0 (2)

В) Найдем из второго (2) уравнения

= 0

= 0



= 0
,
В) Подставляем в первое (1) уравнение и находим

-1

-1

-1

-1


- критическое значение коэффициента усиления системы.
- Определение частоты среза системы.
А) Приведем основные формулы


, где U( ) и V( ) – действительная и мнимая части соответственно.
Б) Подставляем в формулу имеющиеся данные и находим частоту среза системы


В) Найдем (при помощи Wolfram Alpha):

- частота среза системы.
1.Методы классической и современной теории автоматического управления. Том 1.
Анализ и статистическая динамика систем автоматического управления. М: Изд. МГТУ им Баумана. 2000 г.
2. Воронов А.А. Теория автоматического управления. Т. 1-3, М., Наука, 1992
Читайте также:


