Как найти обратную матрицу в excel
Обратная матрица – это сложное математическое понятие, для нахождения которой необходимо выполнить множество непростых действий на бумаге. Однако программа Excel решает данную задачу в более короткие сроки и без особых усилий со стороны исполнителя. Давайте разберемся, каким образом можно найти обратную матрицу в несколько этапов на одном из примеров.
Замечание эксперта! Обязательным условием для нахождения обратной матрицы, является соответствие исходных данных квадратной матрице, а определителя нулю.
Находим значение определителя
Чтобы выполнить это действие, необходимо воспользоваться функцией МОПРЕД. Как именно это делается, рассмотрим на примере:
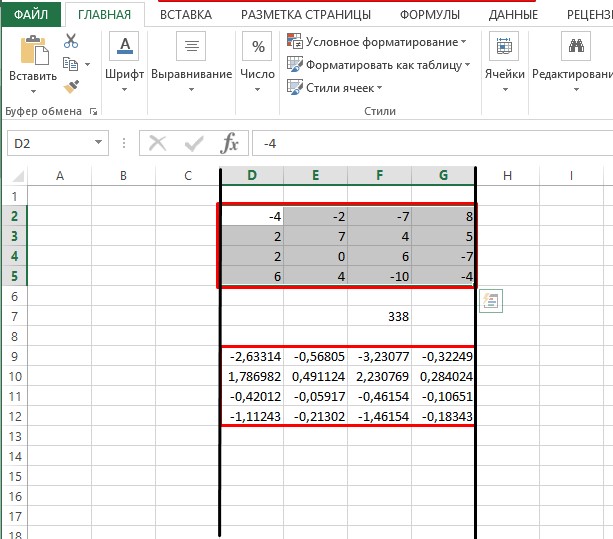
- Записываем квадратную матрицу в любом свободном месте.
- Выбираем свободную ячейку, после чего находим напротив строки формул кнопку «fx» («Вставить функцию») и кликаем по ней ЛКМ.
- Должно открыться окно, где в строке «Категория:» останавливаемся на «Математические», а ниже выбираем функцию МОПРЕД. Соглашаемся с выполненными действиями кликнув по кнопке «ОК».
- Далее в открывшемся окне заполняем координаты массива.
Совет! Заполнить адресацию можно одним из двух способов: вручную или кликнув кнопкой мыши в месте ввода информации о массиве и, определив выделением зоны место расположения квадратной матрицы, получить адрес массива автоматически.
- После проверки введенных ручным или автоматическим образом данных жмите «ОК».
- После всех проведенных манипуляций свободная ячейка должна отобразить определитель матрицы, значение которого понадобится для нахождения обратной матрицы. Как видно по скриншоту, после вычислений получилось число 338, а, следовательно, потому как определитель не равен 0, то обратная матрица существует.
Определяем значение обратной матрицы
Как только вычисление определителя закончено, можно переходить к определению обратной матрицы:
- Выбираем место расположения верхнего элемента обратной матрицы, открываем окно «Вставка функции».
- Выбираем категорию «Математические».
- В расположившихся снизу функциях пролистываем список и останавливаем выбор на МОБР. Кликаем по кнопке «ОК».
- Аналогично ранее выполняемым действиям при нахождении значений определителя вписываем координаты массива с квадратной матрицей.
- Убеждаемся в правильности выполненных действий и жмем «ОК».
- В выбранной верхней левой ячейке будущей обратной матрицы появится результат.
- Для копирования формулы для нахождения значений в других ячейках используем свободное выделение. Для этого, зажав ЛКМ, растягиваем на всю область будущей обратной матрицы.
- Жмем на клавиатуре кнопку F2 и переходим к набору комбинации «Ctrl+Shift+Enter». Готово!
Рекомендация эксперта! Для удобства выполнения действий по нахождению обратной матрицы в таблице Excel расположение массива с квадратной матрицей и выбранная область для ячеек с обратной матрицей должны располагаться на одном уровне по отношению к столбцам. Таким образом будет проще определить границы адресации второго массива. Пример указан на иллюстрации ниже.
Сферы использования расчетов с обратной матрицей
Экономика – это область, которая требует проведения постоянных и очень сложных расчетов. Для облегчения используется матричная система расчетов. Нахождение обратной матрицы – это быстрый способ обработки большого объема информации за максимально короткие сроки, конечный результат которого будет представлен в наиболее удобном для восприятия виде.
Другая область применения – это 3D моделирование изображений. Всевозможные программы имеют встроенные инструменты для проведения подобного рода расчетов, что в значительной степени облегчает работу конструкторам при производстве расчетов. Наиболее популярной программой среди 3D моделистов считается Компас-3D.
Существуют и другие сферы деятельности, где можно применить систему расчетов обратной матрицы, но все же основной программой для проведения матричных расчетов можно считать Excel.
Заключение
Нахождение обратной матрицы нельзя назвать такой же распространенной математической задачей, как вычитание, сложение или деление, но если появилась необходимость в ее решении, то все действия могут произведены в табличном процессоре Excel. Если человеческий фактор склонен допускать ошибки, то компьютерная программа выдаст 100% точный результат.

Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.
Процедура перемножения матриц
Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.
Способ 1: функция МУМНОЖ
Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор МУМНОЖ относится к математической группе функций. Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:
Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.
Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.

-
Выделяем диапазон, где будет отображаться результат умножения, начиная с его верхней левой ячейки. Размер данного диапазона должен соответствовать числу строк у первой матрицы и числу столбцов у второй. Клацаем по пиктограмме «Вставить функцию».




Способ 2: использование составной формулы
Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.
-
На этот раз выделяем на листе только левый верхний элемент массива пустых ячеек, который рассчитываем использовать для вывода результата. Щелкаем по значку «Вставить функцию».


В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.



То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.




Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.

Отблагодарите автора, поделитесь статьей в социальных сетях.


Приложение Excel выполняет целый ряд вычислений, связанных с матричными данными. Программа обрабатывает их, как диапазон ячеек, применяя к ним формулы массива. Одно из таких действий – это нахождение обратной матрицы. Давайте выясним, что представляет собой алгоритм данной процедуры.
Выполнение расчетов
Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.
Расчет определителя
Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.
- Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.




Расчет обратной матрицы
Теперь можно преступить к непосредственному расчету обратной матрицы.
-
Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.





На этом расчет можно считать завершенным.
Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Из определения следует важное свойство, что обратная матрица определена только для квадратных (т.е. число строк и столбцов совпадает) и невырожденных матриц (т.е. определитель отличен от нуля).
Как найти обратную матрицу в Excel?
В отличие от транспонированной матрицы, вычислить обратную матрицу технически несколько сложнее.
Посчитать обратную матрицу можно через построение матриц алгебраических дополнений и определителя исходной матрицы.
Однако сложность вычисления по данному алгоритму имеет квадратичную зависимость от порядка матрицы.
К примеру, для обращения квадратной матрицы 3-го порядка нам необходимо будет дополнительно сделать 9 матриц алгебраических дополнений, транспонировать итоговую созданную матрицу и поэлементно разделить на определитель начальной матрицы, что затрудняет возможность подобного расчета в Excel.
Поэтому воспользуемся стандартной функцией МОБР, которая позволит найти обратную матрицу:
Функция МОБР
Синтаксис и описание функции МОБР в Excel:
МОБР(массив)
Возвращает обратную матрицу (матрица хранится в массиве).
Рассмотрим расчет обратной матрицы посредством функции МОБР на конкретном примере.
Предположим у нас имеется следующая квадратная матрица 3-го порядка:

Выделяем диапазон пустых ячеек E2:G4, куда мы в дальнейшем поместим обратную матрицу.
Не снимая выделения ячеек вводим формулу =МОБР(A2:C4) и нажимаем комбинацию клавиш Ctrl + Shift + Ввод для расчета формулы массива по данному диапазону:

При работе с функцией МОБР могут возникнуть следующие ошибки:
В данной публикации мы рассмотрим, что такое обратная матрица, а также на практическом примере разберем, как ее можно найти с помощью специальной формулы и алгоритма последовательных действий.
Определение обратной матрицы
Для начала вспомним, что из себя представляют обратные значения в математике. Допустим, у нас есть число 7. Тогда обратное ему будет равняться 7 -1 или 1 /7. Если умножить данные числа, в результате получится один, т.е. 7 · 7 -1 = 1.
Почти то же самое и с матрицами. Обратной называется такая матрица, умножив которую на исходную, мы получим единичную. Обозначается она как A -1 .
Алгоритм нахождения обратной матрицы
Для нахождения обратной матрицы нужно уметь вычислять определитель матрицы, а также иметь навыки выполнения определенных действий с ними.
Сразу отметить, что найти обратную можно только для квадратной матрицы, а делается это по формуле ниже:
| A | – определитель матрицы;
A T M – транспонированная матрица алгебраических дополнений.
Примечание: если определитель равен нулю, то обратной матрицы не существует.
Пример
Давайте найдем для матрицы A ниже обратную ей.
Решение
1. Для начала найдем определитель заданной матрицы.
![]()
2. Теперь составим матрицу миноров, которая имеет те же самые размеры, что и исходная:
Нам нужно выяснить, какие числа должны стоять на месте звездочек. Начнем с верхнего левого элемента матрицы. Минор к нему находится путем зачеркивания строки и столбца, в котором он находится, т.е. в обоих случаях под номером один.
Число, которое останется после зачеркивания, и является требуемым минором, т.е. .
Аналогичным образом находим миноры для оставшихся элементов матрицы и получаем такой результат.
3. Определяем матрицу алгебраических дополнений. Как их посчитать для каждого элемента мы рассмотрели в отдельной публикации.
Например, для элемента a11 алгебраическое дополнение считается так:
4. Выполняем транспонирование полученной матрицы алгебраических дополнений (т. е. поменяем столбцы и строки местами).
5. Остается только воспользоваться формулой выше, чтобы найти обратную матрицу.
![]()
Ответ можем оставить в таком виде, не деля элементы матрицы на число 11, так как в этом случае получится некрасивые дробные числа.
Проверка результата
Чтобы убедиться в том, что мы получили обратную исходной матрицу, мы можем найти их произведение, которое должно равняться единичной матрице.
Читайте также:


