Dwg ru построение зубчатого колеса эксель
Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых статьях.
Отписаться от уведомлений вы всегда сможете в профиле автора.
Про моделирование и печать шестеренок здесь написано достаточно. Однако, большинство статей предполагают использование спец. программ. Но, у каждого пользователя есть своя «любимая» программа для моделирования. Кроме того, не все хотят устанавливать и изучать дополнительный софт. Как же моделировать профиль зуба шестерни в программе, где не предусмотрено вычерчивание эвольвентного профиля? Очень просто! Но муторно… :)
Нам понадобится любая программа, которая может работать с 2D графикой. Например, ваша любимая программа! Она работает с 3D? Значит и с 2D сможет! ;) Строим профиль эвольвентного зуба без коррекции. Если кому-то захочется построить корригированный зуб, он может с этим разобраться самостоятельно. Информации полно - и в интернете, и в литературе. Если в вашей шестеренке зубьев больше 17-ти, то вам коррекция не понадобится. Если же зубьев 17 или меньше, то без коррекции возникает «утоньшение» ножки зуба, а при чрезмерной коррекции возникает заострение вершины зуба. Что выбрать? Решать вам.
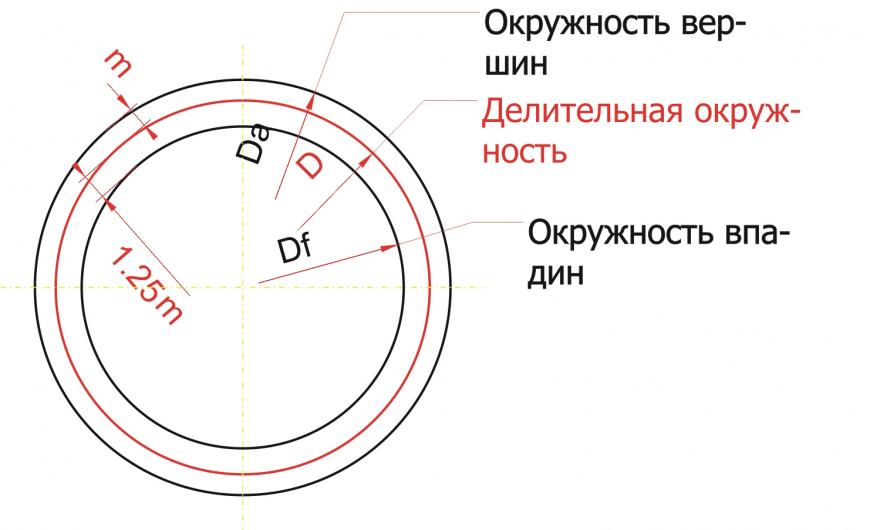
Определяем делительную окружность шестерни. Зачем это нужно? Чтобы определить межосевое расстояние. Т.е. где у вас будет располагаться одна шестерня, а где другая. Сложив диаметры делительных окружностей шестеренок и разделив сумму пополам, вы определите межосевое расстояние.
Чтобы определить диаметр делительной окружности нужно знать два параметра: модуль зуба и количество зубьев. Ну, с количеством зубьев – тут всем все понятно. Количеством зубьев на одной и другой шестерне определяется нужное нам передаточное отношение. Что такое модуль? Чтобы не связываться с числом «пи», инженеры придумали модуль. :) Как вы знаете из курса школьной математики: D= 2 «Пи» R. Так вот, что касается шестеренок, там D = m* z, где D – это диаметр делительной окружности, m – модуль, z – количество зубьев. Модуль – величина, характеризующая размер зуба. Высота зуба равна 2,25 m. Модуль принято выбирать из стандартного ряда величин: 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32 (ГОСТ-9563). Можно ли придумать «свой» модуль? Конечно! Но ваша шестеренка будет нестандартная! ;)
Чертим делительную окружность. У кого нет подходящей «проги», чертит на бумаге, фанере или металле! :) От делительной окружности «откладываем» наружу на величину модуля (m) окружность вершин зубьев. Внутрь откладываем модуль и еще четверть модуля (1,25 m) - получаем окружность впадин зубьев. Четверть модуля дается на зазор между зубом другой шестерни и впадиной этой шестерни.
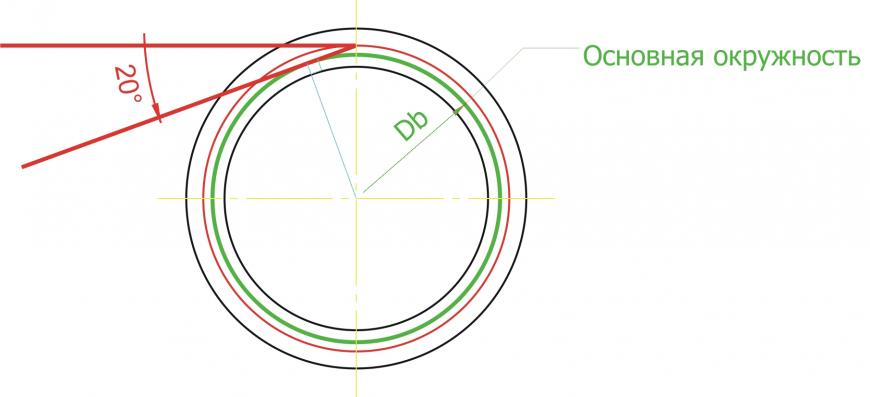
Строим основную окружность. Основная окружность – это окружность, по которой «перекатывается» прямая линия, своим концом вычерчивая эвольвенту. Формула для расчета диаметра основной окружности очень простая: Db = D * cos a, где а – угол рейки 20 градусов. Эта формула нам не нужна! Все гораздо проще. Строим прямую линию через любую точку делительной окружности. Удобнее взять самую высокую точку, на «12 часов». Тогда линия будет горизонтальная. Повернем эту линию на угол в 20 градусов против часовой стрелки. Можно ли повернуть на другой угол? Думаю, можно, но не нужно. :) Кому интересно, ищем в литературе или интернете ответ на вопрос.
Прямую линию, которую мы получили, будем поворачивать вокруг центра шестерни маленькими угловыми шагами. Но, самое главное, при каждом повороте против часовой стрелки будем удлинять нашу линию на длину той дуги основной окружности, которую она прошла. А при повороте по часовой стрелки наша линия будет укорачиваться на ту же величину. Длину дуги или мерим в программе, или считаем по формуле: Длина дуги = (Пи * Db * угол поворота (в градусах)) / 360
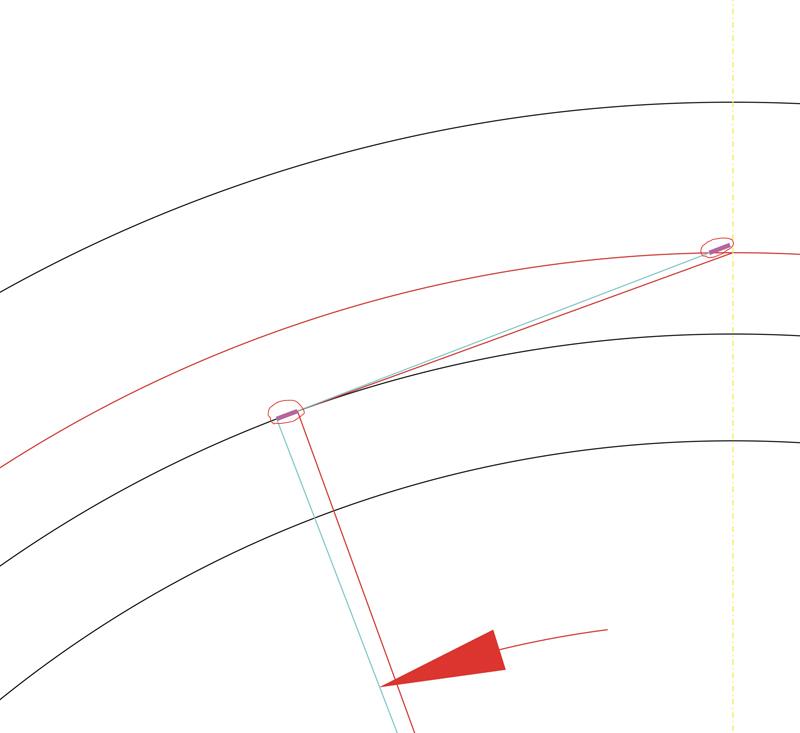
«Прокатываем» прямую линию по основной окружности с нужным угловым шагом. Получаем точки эвольвентного профиля. Чем точнее хотим строить эвольвенту, тем меньший угловой шаг выбираем.
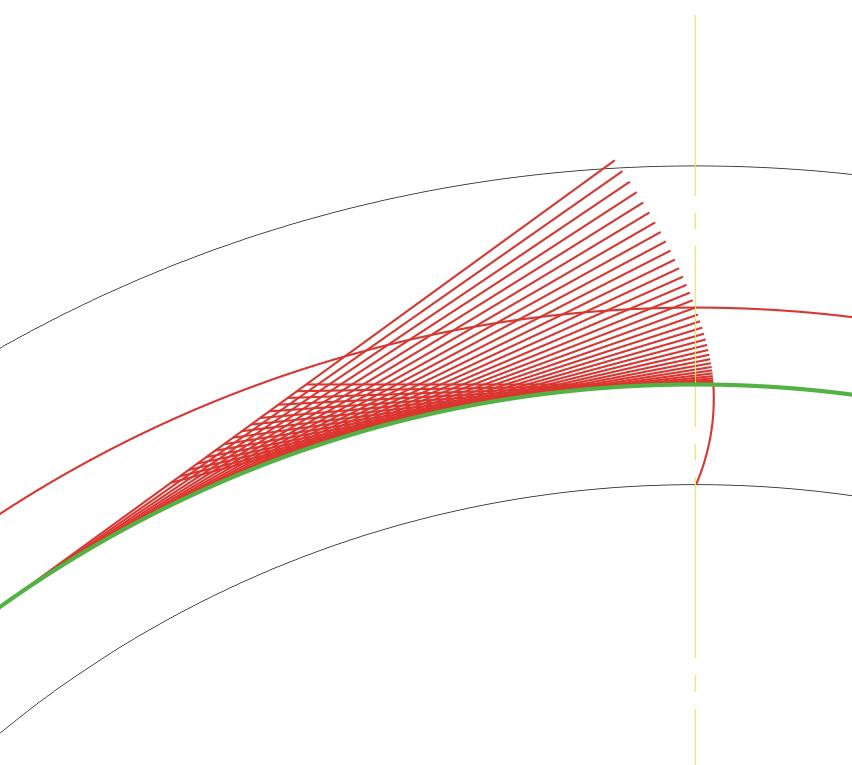
К сожалению, в большинстве программ автоматического проектирования (CAD) не предусмотрено построение эвольвенты. Поэтому эвольвенту строим по точкам либо прямыми, либо дугами, либо сплайнами. При построении эвольвента заканчивается на основной окружности. Оставшуюся часть зуба до впадины можно построить дугой того же радиуса, который получается на трех последних точках. Для 3D печати я рисовал эвольвенту сплайнами. Для лазерной резки металла мне пришлось рисовать эвольвенту дугами. Для лазера нужно создать файл в формате dwg или dxf (для некоторых, почему-то, только dxf). «Понимает» лазер только прямые, дуги и окружности, сплайны не понимает. На лазере можно сделать только прямозубые шестерни.
Делим окружность на такое количество частей, которое в 4 раза больше количества зубьев шестерни. Эвольвенту отзеркаливаем относительно оси зуба и копируем с поворотом нужное количество раз.

Чтобы получить шестерню в объеме, то задаем толщину и получаем прямозубую цилиндрическую шестерню:

Если нужна косозубая шестерня, то вводим наклон зубьев и получаем:

Для получения шевронной шестерни, нужно отзеркалить косозубую шестерню относительно нужной торцевой поверхности:

Как смоделировать коническую шестерню, придумайте сами. :)
К вопросу о точности шестеренок. Те шестеренки, которые я распечатал на 3D принтере, сначала вращались, издавая легкое поскрипывание. Прошло некоторое время, и звук прекратился. Шестеренки «притерлись». :)
После модернизации принтера, шестеренки не печатал. Возможно, сейчас они напечатаются более точно, и не будут скрипеть.
Для вакуумной машины смоделировал пару – «шестерня-рейка». Их вырезали на лазере:
Рейка будет перемещать прижимную рамку с материалом (листовой АБС) из области нагрева в область вакуумного формования. Рейка и шестерня еще не испытывались. Возможно, придется «дорабатывать напильником». На рейке и шестерне видны «волны» от лазера – слишком толстый металл. Они то и могут заклинить. А, может, разработается. :) Время покажет!Подпишитесь на автора
Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых статьях.




Записи в блогах
Пользовательская команда для включение/выключение маски заднего фона для м/текстов/выносок/размеров.
1. Для собственного "общего развития". 2. Просто интересно, что и как. Какие-то личные открытия уже появились. 3. Ковид и самоизоляция. 4. Вдруг куда-то еще вырулится. 5. Всегда лучше иметь больше и разных возможностей. 6. Если уж нашел что-то, то нормально поделиться. Это пилотный, поисковый и неожиданный для меня самого проект.
Немного о налогах и о том, что в заголовке. Ссылка на китайское руководсво по КЖ и КМ как бонус
Гидроизоляция "Пенетрон" использована для защиты транспортно-логистического комплекса "Южноуральский".
Информационный Youtube-канал "PRO-Z: Проектирование зданий" для проектировщиков, строителей, заказчиков. - справочная информация; - проекты; - курсы; - консультации
nanoCAD BIM Day – первая официальная презентация BIM-концепции компании «Нанософт разработка». На конференции мы продемонстрируем наше комплексное BIM-решение, представим долгожданные новинки, поделимся лучшими BIM-проектами и ответим на вопросы пользователей.
Библиотека

Отличительной чертой программы «Расчет геометрии зубчатой цилиндрической эвольвентной передачи», представленной в этой статье, является ее универсальность. С помощью предложенной программы можно выполнить расчет прямозубых и косозубых эвольвентных передач.
. наружного и внутреннего зацепления со смещением исходного контура и без смещения.
В статье «Расчет зубчатой передачи» мной предложена программа «Проектировочный расчет цилиндрической зубчатой передачи», которая на основе заданных силовых и кинематических параметров определяет основные габаритные. Эти величины для сегодняшнего нашего расчета станут исходными данными.
Геометрический расчет зубчатой передачи выполним в программе MS Excel.
При отсутствии у вас на компьютере программы MS Excel воспользуйтесь бесплатной программой OOo Calc из пакета Open Office.
Целью данного расчета является нахождение ряда размеров (углов и диаметров), необходимых для окончательного оформления рабочих чертежей колеса и шестерни, а так же для выполнения в дальнейшем проверочных расчетов качества зубчатого зацепления по геометрическим показателям.
Ссылка на файл с программой – в конце статьи.
Схема наиболее распространенного наружного зубчатого зацепления в торцевом сечении показана на рисунке, расположенном ниже этого текста.

Исходные данные записываем в ячейки со светло-бирюзовой заливкой. В ячейки с бледно-голубой заливкой вносим исходные данные, внимательно выполнив требования, помещенные в расположенной над ними строке! Результаты расчетов считываем в ячейках со светло-желтой заливкой. В ячейках со светло-зеленой заливкой, как обычно, помещены мало подверженные изменениям исходные данные.
Открываем таблицу файла Excel и записываем исходные данные:
1. Констатируем в объединенной ячейке D3E3, что параметры нормального исходного контура, участвующие в расчете, взяты по ГОСТ 13755-82. В примечании к объединенной ячейке D3E3 указано: угол исходного профиля a =20 градусов; коэффициент высоты головки зуба ha* =1; коэффициент радиального зазора c* =0,25.
2. Тип зацепления T (смотри примечание: T =1 – наружное; T =-1 – внутреннее зацепление) указываем
в объединенной ячейке D4E4: 1
3. Модуль зацепления m в миллиметрах (в примечании – стандартный ряд модулей) вписываем
в объединенную ячейку D5E5: 1,5
4. Угол наклона зубьев b в градусах (в примечании – рекомендации по назначению) вписываем
в объединенную ячейку D6E6: 13,3222
5. Число зубьев z1 и z2 заносим соответственно
в ячейку D7: 18
и в ячейку E7: 73
6.1. Далее, если известно из предыдущих расчетов межосевое расстояние aw , то вписываем это значение в миллиметрах
в объединенную ячейку D9E9: _____
Если значение aw не известно, то оставляем ячейку D9E9 пустой! (В примере межосевое расстояние не определено.)
6.2. Если заданы коэффициенты смещения исходного контура x1 и x2 (и соответственно не задано aw !), то вписываем эти значения
в ячейку D10: 0,300
и в ячейку E10: 0,300
Если значения x1 и x2 не заданы, то ничего не записываем в ячейки D10 и E10!
Почему, как и зачем назначать смещение исходного контура, выполняя геометрический расчет зубчатой передачи, мы постараемся обсудить на страницах блога (при наличии интереса аудитории) в статьях, которые будут опубликованы в будущем.
Чтобы не пропустить выход статей, получайте анонсы. Для этого необходимо подписаться в окне, расположенном вверху страницы. Введите адрес своей электронной почты и нажмите на кнопку «Получать анонсы статей», подтвердите подписку в письме, которое тут же придет к вам на указанную почту!

После ввода исходных данных программа расчета геометрии зубчатой передачи представляет первый блок автоматически рассчитанных искомых параметров:
7. Передаточное число u рассчитано
в объединенной ячейке D12E12: =E7/D7 =4,056
u = z2 / z1
8. Делительные диаметры d1 и d2 в миллиметрах вычислены соответственно
в ячейке D13: =D5*D7/COS (D6/180*ПИ()) =27,747
d1 = m * z1 /cos( b )
и в ячейке E13: =D5*E7/COS (D6/180*ПИ()) =112,528
d2 = m * z2 /cos ( b )
9. Делительное межцентровое расстояние A в миллиметрах рассчитано
в объединенной ячейке D14E14: =(E13+D4*D13)/2 =70,137
A =( d2 + T * d1 )/2
10. Угол профиля at в градусах рассчитан
в объединенной ячейке D15E15: =ATAN (TAN (20/180*ПИ())/COS (D6/ 180*ПИ()))/ПИ()*180 =20,5076
at =arctg(tg ( a )/cos ( b ))
11. Диаметры основных окружностей db1 и db2 в миллиметрах вычислены соответственно
в ячейке D16: =D13*COS (D15/180*ПИ()) =25,988
db1 = d1 *cos ( at )
и в ячейке E16: =E13*COS (D15/180*ПИ()) =105,397
db2 = d 2 *cos( at )
12. Угол зацепления atw в градусах рассчитан
в объединенной ячейке D17E17: =ЕСЛИ(D9=0;D50/ПИ()*180;ACOS ( D14*COS (D15/180*ПИ())/D9)/ПИ()*180) =22.2962
Если расстояние между центрами колеса и шестерни не задано, то угол зацепления находится путем решения численным методом трансцендентного уравнения:
tg ( atw ) — atw =2* xs *tg ( a )/( z2 + T * z1 )+ tg ( at ) — at
Подробно о том, как это делается и, что такое трансцендентные уравнения, я постараюсь доступно рассказать в одной из ближайших статей рубрики «Справочник Excel».
Если межосевое расстояние задано, то угол зацепления вычисляется по формуле:
atw =arcos ( A *cos ( at )/ aw )
13. Коэффициент суммы xs (разности — для передач с внутренним зацеплением) смещений вычислен
в объединенной ячейке D18E18: =ЕСЛИ(D9=0;E10+D4*D10;(E7+D4*D7)*((TAN (D17/180*ПИ()) -D17/180*ПИ()) — (TAN (D15/180*ПИ()) -D15/180*ПИ()))/(2*TAN (20/180*ПИ()))) =0,6000
Если межцентровое расстояние не задано, то коэффициент суммы (разности) находится по формуле:
xs = x 2 + T * x1
Если межцентровое расстояние задано, то коэффициент суммы (разности) вычисляется по формуле:
xs =( z2 + T * z1 )*((tg ( atw ) - atw ) — (tg ( at ) - at ))/(2*tg ( a ))
Далее – короткая работа интеллекта инженера, и программа завершает геометрический расчет в Excel зубчатой передачи:
14. Если коэффициенты смещения были заданы, то просто повторно записываем значение x1
в ячейку D20: 0,3000
Если коэффициенты смещения x1 и x2 изначально заданы не были (было задано межосевое расстояние aw ), то на этом этапе необходимо произвести разбивку вычисленного коэффициента суммы (разности) смещений xs и записать в ячейку D20 значение x1 .
Рекомендации по разбивке коэффициента суммы (разности) смещений можно посмотреть в ГОСТ 16532-70 и в соответствующих справочниках (в том числе В.И.Анурьева).
Значение коэффициента смещения x2 вычисляется автоматически
x2 = xs — T * x1
15. Межосевое расстояние передачи aw в миллиметрах, если не задано — вычислено, если задано – автоматически повторено
в объединенной ячейке D21E21: =ЕСЛИ(D9=0;D14*COS (D15/180* ПИ())/COS (D17/180*ПИ());D9) =71,001
aw = A *cos ( at )/cos ( atw )
16. Диаметры начальных окружностей dw1 и dw2 в миллиметрах вычислены соответственно
в ячейке D22: =2*D21/(D12+D4) =28.088
dw1 =2* aw /( u + T )
и в ячейке E22: =2*D21*D12/(D12+D4) =113.914
dw2 =2* aw * u /( u + T )
17. Коэффициент уравнительного смещения dy рассчитан
dy = xs — ( aw — A )/ m
18. Диаметры вершин зубьев шестерни и колеса da1 и da2 в миллиметрах вычислены соответственно
в ячейке D24: =D13+2*D5*(1+D20-D23) =31.574
da1 = d 1 +2* m *(( ha * )+ x 1 — dy )
и в ячейке E24: =E13+2*D5*D4*(1+D4*E20-D23) =116.355
da2 = d2 +2* m * T *(( ha* )+ T * x2 - dy )
В обоснованных случаях значения, полученные расчетом конструктор вправе изменить, обеспечив качественные характеристики зацепления.
19. Диаметры впадин шестерни и колеса df1 и df2 в миллиметрах вычислены соответственно
в ячейке D25: =D24-2*D5*(2*1+0,25-D23) =24.897
df1 = da 1 -2* m *(2*( ha * )+( c * ) — dy )
и в ячейке E25: =E24-2*D5*D4*(2*1+0,25-D23) =109.678
df2 = da2 -2* m * T *(2*( ha* )+( c* ) - dy )
На этом геометрический расчет в Excel цилиндрической зубчатой передачи, целью которого было определение всех основных размеров зацепления завершен. При создании расчетной программы была объединена и переработана информация из ГОСТ 16532-70 и ГОСТ 19274-73.
Следующим этапом проектирования зубчатых передач являются проверочные расчеты качества зацепления по геометрическим показателям.
Еще по теме зубчатых колес на блоге есть ряд статей. Рекомендую ознакомиться, в частности, со статьей «Расчет длины общей нормали зубчатого колеса».
Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
ОСТАЛЬНЫМ можно скачать просто так. — никаких паролей нет!

Урок посвящен построению зубчатого колеса с эвольвентным профилем зуба. Урок состоит из двух частей. В первой части выложена теория, формулы для расчета и один из способов графического построения эвольвентного профиля зуба.
Во второй части (видео) показан способ построения модели зубчатого колеса с использованием графических построений в первой части урока.
Часто задаваемые вопросы:
*Что такое эвольвента (эволюта)?
*Как построить эвольвенту?
*Как построить зубчатое колесо в программе SolidWorks?
*Формулы для расчета зубчатого колеса?
*Как нарисовать эвольвентный профиль зуба зубчатого колеса?
Итак, начнем с теории.
Эвольвентное зацепление позволяет передавать движение с постоянным передаточным отношением. Эвольвентное зацепление - зубчатое зацепление, в котором профили зубьев очерчены по эвольвенте окружности.
Для этого необходимо чтобы зубья зубчатых колёс были очерчены по кривой, у которой общая нормаль, проведённая через точку касания профилей зубьев, всегда проходит через одну и туже точку на линии, соединяющей центры зубчатых колёс, называемую полюсом зацепления.
Параметры зубчатых колёс
Основной теореме зацепления удовлетворяют различные кривые, в том числе эвольвента и окружность, по которым чаще всего изготавливают профили зубьев зубчатого колеса.
В случае, если профиль зуба выполнен по эвольвенте, передача называется эвольвентной.
Для передачи больших усилий с помощью зубчатых механизмов используют зацепление Новикова, в котором профиль зуба выполнен по окружности.
Окружности, которые катятся в зацеплении без скольжения друг по другу, называются начальными (D).
Окружности, огибающие головки зубьев зубчатых колёс, называются окружностями головок (d1).
Окружности, огибающие ножки зубьев зубчатых колёс, называются окружностями ножек (d2).
Окружности, по которым катятся прямые, образующие эвольвенты зубьев первого и второго колёс, называются основными окружностями.
Окружность, которая делит зуб на головку и ножку, называется делительной окружностью (D).
Для нулевых (некорригированных) колёс начальная и делительная окружности совпадают.
Расстояние между одноимёнными точками двух соседних профилей зубьев зубчатого колеса называется шагом по соответствующей окружности.
Шаг можно определить по любой из пяти окружностей. Чаще всего используют делительный шаг p =2r/z, где z – число зубьев зубчатого колеса. Чтобы уйти от иррациональности в расчётах параметров зубчатых колёс, в рассмотрение вводят модуль, измеряемый в миллиметрах, равный
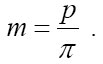
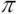
Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности (D) к числу зубьев z или отношению шага p к числу "пи" .
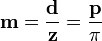
Модуль зубчатого колеса стандартизованы, что является основой для стандартизации других параметров зубчатых колёс.
Основные формулы для расчета эвольвентного зацепления:
Исходными данными для расчета как эвольвенты, так и зубчатого колеса являются следующие параметры: m - Модуль - часть диаметра делительной окружности приходящаяся на один зуб. Модуль - стандартная величина и определяется по справочникам. z - количество зубьев колеса. ? ("альфа") - угол профиля исходного контура. Угол является величиной стандартной и равной 20°.
Делительный диаметр рассчитывается по формуле:
Диаметр вершин зубьев рассчитывается по формуле:
d1=D+2m
Диаметр впадин зубьев рассчитывается по формуле:
d2=D-2*(c+m)
где с - радиальный зазор пары исходных контуров. Он определяется по формуле:
с = 0,25m
Диаметр основной окружности, развертка которой и будет составлять эвольвенту, определяется по формуле:
d3 = cos ? * D
От автора. Я нашел в интернете полезную программку в Excel 2007. Это автоматизированная табличка для расчета всех параметров прямозубого зубчатого колеса.
Итак, приступим к графическому построению профиля зубчатого колеса.
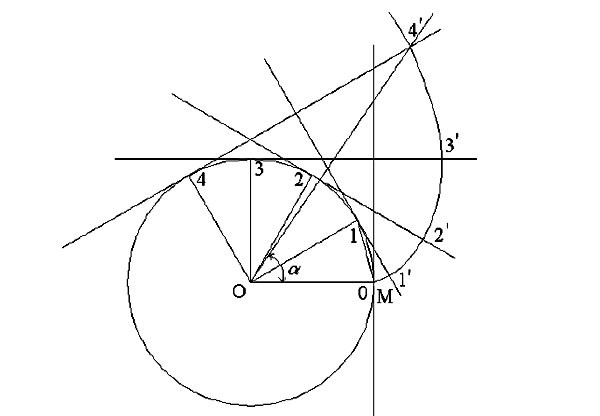
- Изобразите делительный диаметр с диаметром D, и центром шестерни O. Окружность показана красным цветом.
- Изобразите диаметр вершин зубьев (d1) с центром в точке O с радиусом большим на высоту головки зуба(зелёного цвета).
- Изобразите диаметр впадин зубьев (d2) с центром в точке O с радиусом меньшим на высоту ножки зуба (голубого цвета цвета).
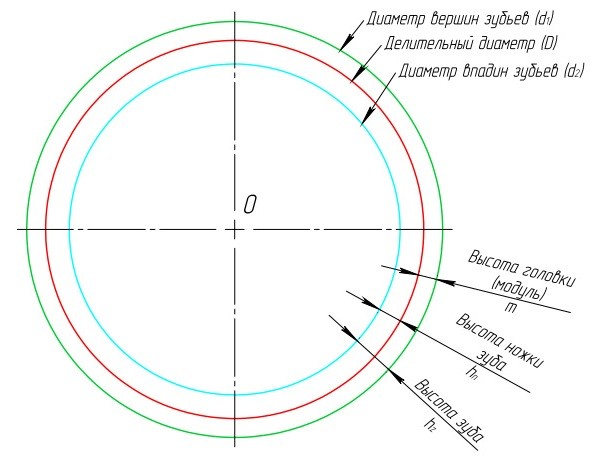
- Проведите касательную к делительному диаметру (желтая).
- В точке касания под углом ? проведите линию зацепления, оранжевого цвета.
- Изобразите окружность касательную к линии зацепления, и центром в точке O. Эта окружность является основной и показана тёмно синего цвета.
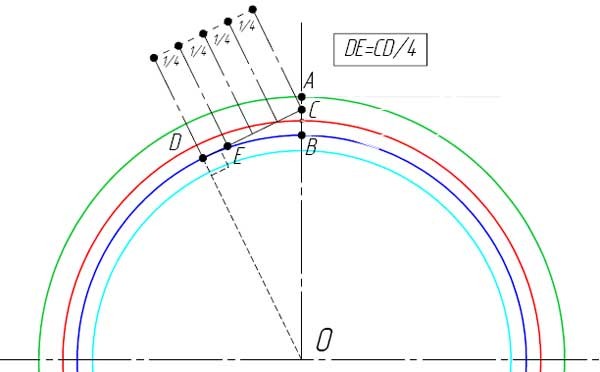
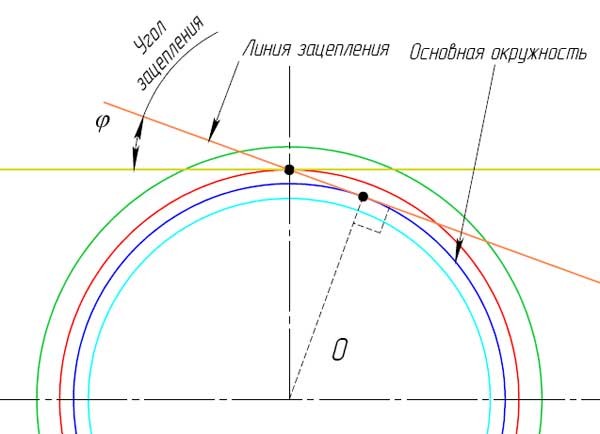
- От точки C проведите касательную к основной окружности.
- В точке касания отметьте точку D.
- Разделите расстояние DC на четыре части и отметьте, точкой E, полученное значение от точки D в сторону точки C на отрезке DC.
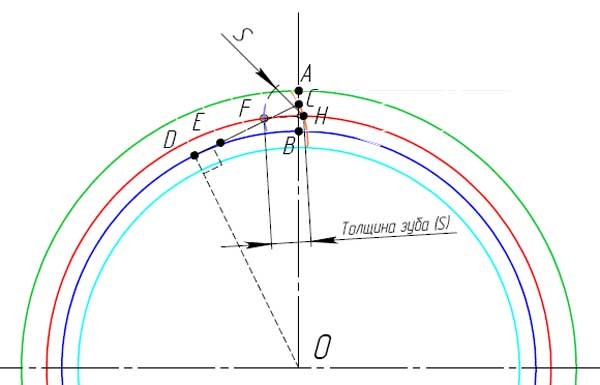
- Изобразите дугу окружности с центром в точке E, что проходит через точку C. Это будет часть одной стороны зуба, показана оранжевым.
- Изобразите дугу окружности с центром в точке H, радиусом, равным толщине зуба (s). Место пересечения с делительным диаметром отметьте точкой F. Эта точка находится на другой стороне зуба.
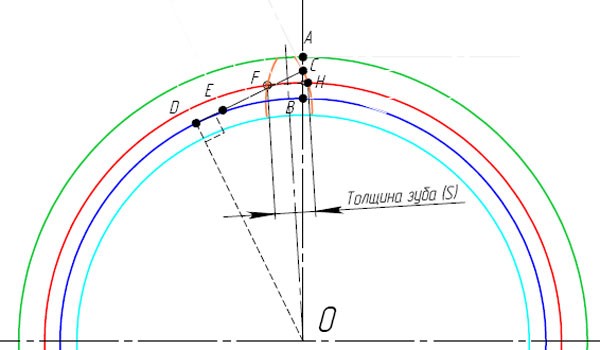
- Изобразите ось симметрии проходящую через центр О и середину расстояния FH.
- Линия профиля зуба отображенная зеркально относительно этой оси и будет второй стороной зуба.
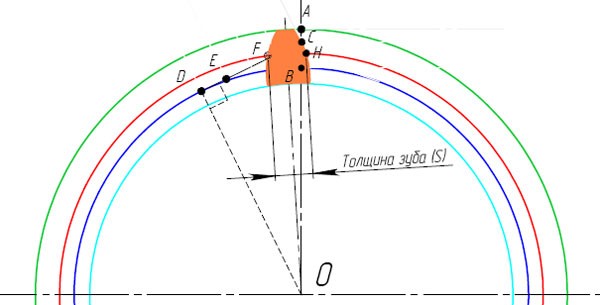
Вот и готов профиль зуба прямозубого зубчатого колеса. В этом примере использовались следующие параметры:
На этом первая часть урока является завершенной. Во второй части (видео) мы рассмотрим как применить полученный профиль зуба для построения модели зубчатого колеса. Для полного ознакомления с данной темой ("зубчатые колеса и зубчатые зацепления", а также "динамические сопряжения в SolidWorks") необходимо вместе с изучением этого урока изучать урок №24.
Еще скажу пару слов о специальной программе, производящей расчет зубчатых колес и генерацию модели зубчатого колеса для SolidWorks. Это программа Camnetics GearTrax.

Ваш плагин под inkscape тоже супер, но не разобрался как внутренний зуб сделать (если есть такая фича)
Утром в газете, вечером в буфете.
Перегнал в stl, вечером отправил по мейлу в одну контору, утром готово.
Результат порадовал, шестерни сели с натягом, фаску таки надо предусматривать.
Жду результата нарезки на лазере из Ст-1 6 мм г.к. (сорри, наверное уже офтоп пошел)
Пластик ABS. Диаметр внешней звезды 109 мм
Вложения Твердая копия планетарки - печать на 3d принтере magnetic писал(а): Пластик ABS. Диаметр внешней звезды 109 ммUse the Console, Luke.

Да, спасибо, я тоже учился в институте. у меня к сожалению нет доступных спецзубоизготовительных станков. В посте написал, что цель - познавательная. Заказывал резку большого комплекта, за одно и это.
Делюсь результатом, а точнее, в рамках раздела форума, показал применимость ПО, что по ссылке, практически, с применением различных инструментов.
magnetic писал(а): В посте написал, что цель - познавательная C этим всё понятно, я просто к тому, что лазер не лучший станок для шестерней Я не матерюсь, а всего лишь употребляю ненормативную лексику в целях более полного и лаконичного выражения своих эмоций.Абсолютно согласен, что лазер не тот инструмент для зубчатых колес, но поскольку отвечаю за ссылку, то счел своим долгом материализовать )))
ЗЫ: На самом деле сделал эти наборы шестерен для отца, он делает вечный двигатель многополюсной электрический двигатель на постоянных магнитах и попросил меня планетарку сочинить, металлической обрадовался как ребенок В общем и с сообществом поделился, и сам позабавился и дедушку порадовал. Всем мир!
Читайте также:


