Бифуркационная диаграмма как построить в excel

1. Сценарий перехода в хаос (Эта часть работы выполняется в Excel).
Логистическое уравнение имеет следующий вид:
Это уравнение представляет собой одномерную нелинейную систему с обратной связью. Такое уравнение может быть исследовано в электронной таблице Excel, для чего необходимо выполнить следующие шаги:
1. В ячейку А1 поместить начальное значение постоянной А между 0 и 4. Начать со значения А = 2.
2. В ячейку В1 поместить начальное значение х = 0,1.
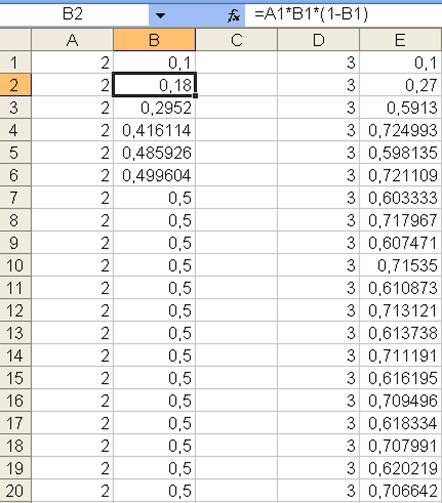
3. В ячейке В2 поместить формулу: =А1*В1*(1 – В1).
4. Скопировать ячейку В2 вниз, по крайней мере, на 100 ячеек. Пример выполнения показан ниже (только на 20 точек).
5. Построить график по данным колонки В. Пример на рис.1.
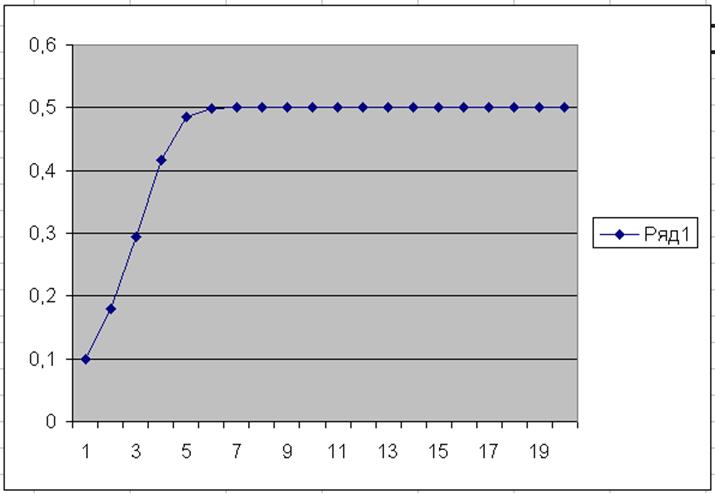
6. Положить значение А = 3. Повторить пп.2 -5.
7. Положить значение А = 3,48. Повторить пп.2 -5.
8. Положить значение А = 3,6. Повторить пп.2 -5.
9. Построить бифуркационную диаграмму (по оси абсцисс -значения А; по шкале ординат - значения х).
2. Отображение Хенона описывается следующей системой уравнений:
Построить аттрактор Хенона следующим образом:
1.В ячейки А1 и В1 поместить начальные величины х и у, выбранные в диапазоне от 0 до 1.
2. В ячейку А2 поместить выражение: = 1 + В1 – 1,4 * А1 2 .
3. В ячейку В2 поместить выражение: = 0,3*А1.
4. Скопировать А1 и В2 вниз на 100 строк или более (чем больше, тем лучше).
5. Построить диаграмму (аттрактор Хенона), используя значения столбца А как абсциссу, а значения столбца В - как ординату.
3. Расчет показателя Херста с помощью программы Fractan
1. Открыть файл "Ценные бумаги Марков". Этот файл содержит данные по ценам акций различных российских предприятий. Выбрать какие-либо акции (на протяжении примерно 1400 торговых дней, цену открытия или другую цену), скопировать этот временной ряд.
2. Открыть блокнот и вставить в него полученный временной ряд.
3. Заменить в этих данных запятую (,) на точку (.).
4. Сохранить ряд с расширением .dat.
5. Открыть программу Fractan, вставить в него анализируемый ряд, рассчитать показатель Херста . Оценить значение показателя.
6. В этом же пакете произвести расчет показателя Херста для различных временных рядов, имеющихся в пакете.

Однажды для презентации мне понадобились анимированные графики. С графиками, собственно, проблем не возникло, а для их анимации пришлось воспользоваться еще одним пакетом animation , который можно установить из CRAN.
Стоит отметить, что animation в процессе обработки изображений использует пакет программ ImageMagick, так что его желательно установить заранее. Под Windows работоспособность этого решения я не проверял.
Для создания анимированного графика нам, в общем-то, понадобится всего одна функция такого вида:
Так получилось, что в то время я проходил весьма познавательный курс Introduction to Dynamical Systems and Chaos, и мне было интересно, как от относительно простых математических объектов переходят к весьма причудливым изображениям. Взять хотя бы логистическое отображение такого вида:
Эту итерационную функцию можно интерпретировать как зависимость численности популяции от ее величины в предыдущий период времени и от параметра r , который обычно называют скоростью размножения. Собственно, сама по себе функция довольно унылая и имеет весьма банальный график. Интересные вещи проявляются, если рассматривать ее бифуркационную диаграмму: изменяя параметр r , можно наблюдать «динамику» неподвижных точек уравнения. Запишем логистическое отображение в R в виде такой функции:
Зададим некоторые интересные точки и начальные параметры для отображения и построим бифуркационную диаграмму, изменяя масштаб изображения по ходу дела:
Можно заметить, что количество неподвижных точек уравнения удваивается, образуя таким образом каскад бифуркаций и проявляя фрактальную структуру. Тут еще уместно вспомнить о таком феномене, как универсальность. Рассмотрим два уравнения:


Первое уравнение определяет расстояние от одной точки бифуркации до следующей в единицах r . Второе же показывает, насколько ответвление n длиннее ответвления n+1. Так вот, оказывается, что

Число 4.669201… называется универсальной постоянной Фейгенбаума, которая как раз и характеризует скорость перехода динамических систем от порядка к детерминированному хаосу.
Другой интересный и не менее известный объект — аттрактор Лоренца. На Хабре ему даже посвящена отдельная статья. Для описания движения воздушных потоков Эдвард Лоренц использовал систему из трех обыкновенных дифференциальных уравнений, известных теперь как уравнения Лоренца:

Не будем изголяться и решим эту систему численно — методом Эйлера:
Решение системы для параметров, заданных по умолчанию, выглядит так:

Изменяя параметр r, можно получить серию изображений, на которых видно, как происходит эволюция системы от начальных условий и неподвижной точки к, собственно, странному аттрактору.

Хвостом будем считать череду структур к западу от центральной кардиоиды вдоль по отрицательной части вещественной оси. В этой области таится целая бездна деталей. А в деталях, как известно, кроется дьявол … и его малютки.
Данная статья продолжает серию об устройстве множества Мандельброта.
Ранее мы изучали:
Большой довесок
Так будем называть круг множества Мандельброта с центром в точке (-1, i*0) и радиусом ¼.

Фиг.1 большой довесок
Точка (-1, i*0) забавная, после возведения в квадрат превращается в (1, i*0), после добавления константы становится (0, i*0). На второй итерации возвращается в исходное положение.
Попробуем провернуть тот же трюк, что удался при исследовании центральной кардиоиды — посмотрим куда сходятся траектории, начинающиеся с приграничных точек.

Фиг.2 финальные точки траекторий, стартующих с периметра “большого довеска”
starting circle — круг с центром в (-1, 0 i) и радиусом 0.2495. Честный радиус — 0.25, но точки с него сходятся крайне медленно.
final — по две точки на каждую стартовую. Обладают центральной симметрией относительно точки (-0.5, 0 i). Между углами в исходном круге и param разница в .
Показана только половина соединяющих линий. Шаг — полтора градуса.
param — экспериментально полученная параметрическая кривая , сдвинутая на (-0.5, 0 i).
Вообще, кривая param имеет четыре лепестка — два в вещественной области и два в мнимой. Это звучит странно т.к. мы уже находимся в комплексной плоскости.
Для начала проверим что две чисто вещественные точки переходят друг в друга.
Возьмём минимальную точку (-1¼, 0 i)
- для кривой param угол
- константа C Из равна
- сама param в этой точке
- квадрат param
- добавляем константу
- разберем отрезок ,
в этой области неотрицателен, как раз то что нужно - константа C Из равна
- угол окружности () и угол param () судя по приведенному графику связаны как или
- радиус param равен
В этой области отрицателен. Пусть .
Тогда param:.
Фактически, мнимые лепестки развернулись и легли поверх действительных.
Если бы не это, пришлось бы ломать голову, почему при мы попадаем на вещественные лепестки, а при нет.
Есть всё же в этом какая-то натяжка. Осталось ощущение очень мелкой возни и упущенной общей картины. Но по крайней мере теперь у нас в наличии есть оба элементарных блока из которых построено всё множество — круг и кардиоида. Осталось научиться смешивать их в нужных пропорциях.
Малые довески
Так станем называть более мелкие образования, нанизанные на отрицательную часть оси Re[C].
Минимальное значение, при котором последовательность, стартующая с оси Re[C] не расходится, это -2.
- -2 превращается в +4
- +4 при добавлении константы становится +2
- +2 превращается в +4
- .
А что происходит в интервале [-2:-1.25]?
Пройдёмся по этому отрезку и нарисуем предельные траектории, полученные с точек на нём. Поскольку мнимая часть на этом отрезке (для всех точек траектории) отсутствует, получается вполне наглядное представление — стартовая точка против финальных траекторных.
Финальными траекторными будем считать точки, полученные с помощью следующей эвристики.
- первые 9000 итераций: делаем, но никак не учитываем.
- следующие 1000 итераций: запоминаем точки траектории с точностью до 4 знаков после запятой
- то, что накопили в результате и есть финальные точки, их может быть от 1 до 1000.
Здесь для наглядности приведена часть множества Мандельброта в том же масштабе, соответствующая рассматриваемому отрезку.
Имеем дело с бифуркационной диаграммой для последовательности .
- на интервале -0.75. 0 последовательность сходится к одной точке, это соответствует центральной кардиоиде
- в точке -0.75 происходит бифуркация и последовательность выходит на предельный цикл из двух точек. Это область “большого довеска”. С центром в точке -1, для которой предельный цикл (-1 => 0 => -1).
- Далее идёт цепочка бифуркаций, при этом, как и положено, бифуркационный параметр при каждой следующем удвоении периода меняется всё меньше. Предел отношения последовательных изменений бифуркационного параметра называется постоянная Фейгенбаума и примерно равен 4.669. Этот предел универсален для всех рекуррентных последовательностей 2-й степени.
- Промежуток между бифуркациями на множестве Мандельброта соответствует кругу диаметра, равного этому промежутку.
- Однако, при соотношении диаметров 1 к 4.669, последовательность кругов очень быстро сходится, примерно при значении -1,40116 наступает предел. Назовём его “горизонт событий”.
- Но жизнь продолжается и за горизонтом событий.

Фиг.4 фрагмент бифуркационной ддиаграммы
Каждый раз, когда мы видим на диаграмме “прогалину”, ей соответствует не просто окружность, а миниатюрная копия множества Мандельброта, со своей кардиоидой, большим и малыми довесками…
Что объединяет все такие структуры?
Чем они отличаются от “довесков”?
Здесь наглядности, стоит привести бифуркационный “спектр” — зависимость длины предельного цикла от константы. Спектр получен с помощью эвристики и имеет значение только для оценки общей картины.

Фиг.6 бифуркационный спектр c шагом в 0.001

Фиг.7 спектр с разными шагами
Чем меньше шаг, тем больше выявляется циклов разной длины. Обратим внимание на характерные “лесенки” — удвоения периодов не только в изначальном каскаде бифуркаций, но и во всех “прогалинах/окнах периодичности”. Глядя на них невозможно не упомянуть теорему Шарковского

Фиг.8 порядок Шарковского

Оператор x y означает, что если существует цикл длины x, обязан быть и цикл длины y. Нижняя строка соответствует начальному каскаду бифуркаций.
Лесенки у окон периодичности — столбцам вплоть до последней строки. С первой строкой, похоже, придётся повозиться.
Но вернёмся к бифуркационной диаграмме.
Вцелом картина неясна, поэтому зацепимся за что-нибудь, поддающееся осмыслению, потянем за эту ниточку и потихоньку распустим весь клубок.

Удачный кандидат быть такой ниточкой — самое большое окно за “горизонтом событий” — [-1.7684:-1.75] с длиной цикла 3. Взглянем поближе на все три непустых фрагмента этого окна.
Фиг.9 Центральная часть большого окна.

Фиг.10 Верхняя часть

Фиг.11 Нижняя часть
- Как по команде, без перехода, в -1.75 хаос заканчивается и дальше идёт серия бифуркаций
- Заканчивается всё собственным “горизонтом событий” этого окна.
- Бифуркации во всех трёх ветках происходят синхронно.
- Отрезок [-1.768:-1.75] соответствует местной кардиоиде, ниже идёт локальный “большой довесок” …
- В -1.755 (примерно) центральная часть пересекает 0 и это соответствует 0 для основной кардиоиды множества Мандельброта.
- В -1.755 нижняя часть равна -1.755
- Имеем цикл длины 3.
- Одна из точек цикла — 0.
- Из этого следует, что следующая точка цикла ,
в данном случае -1.755. - Последняя точка цикла =>
- Но что это за число -1.755, можно ли его получить аналитически?
- Будем исходить из того, что в основной кардиоиде в точке ноль траектория так и оставалась в 0, никуда не мигрировала, здесь должно быть то же самое.
- запишем переходы
Фиг.12 Наложение полинома на бифуркационную диаграмму

Фиг.14 Фазовая диаграмма траекторий циклов длины
3, по X — предыдущее значение, по Y — текущее.
‘pp3center’ — проходит через 0
‘pp3start’ — максимальное значение диапазона, тоже длины 3,
‘pp3fin’ — за пределами диапазона цикл расщепился до длины 24.
Движение везде по часовой стрелке.
Лирическое отступление. Есть такое устойчивое выражение “period three implies chaos” (в порядке Шарковского всё начинается именно с трёх), то что мы наблюдаем проливает свет, почему именно 3.
В самом деле, из этих трёх два являются “обязательной программой” — 0 и начальное значение константы. Любое наблюдаемое окно периодичности содержит (центральную, основную, базовую?) траекторию, проходящую через 0. Почему, это отдельный вопрос, постараемся ответить на него позже. Но где есть 0, на траектории будет и начальная константа. А без этой парочки 3 превращается в 1, меньше которой уже и нет ничего. Т.е. есть циклы длины 1 и 2, которые мы видели и до “горизонта событий” в регулярной части бифуркационной диаграммы. Причем, цикл длины 2 сам является “обязательной программой”, а длины 1 — ещё и вырожденной оной.
А как насчет циклов большей длины? Судя по бифуркационной диаграмме с наложенными модами, если требуется найти цикл длины n, стоит поискать 0 для функции . Это довольно просто проверить, для этого
- в gnuplot строится график , например
- на графике можно с приличной точностью найти один из вещественных корней, например, -1.9893204
- в любом онлайн — просмотре множества Мандельброта отмасштабироваться в нужную точку и voilà

Фиг.15 возможный фрактал, соответствующий одному из корней моды
- до сих пор мы воспринимали траекторию как нечто цельное и уже полученное, на самом деле это итеративный процесс
- т.е. сначала вычисляется затем …
- Допустим, мы дошли до и случайно попали в стационарную точку, т.е. такую x, где ,
Стартовые константы получены вышеописанным образом из gnuplot.

Фиг.16 Фазовая диаграмма траекторий циклов длины 4, в названии стартовая константа
‘pp4-1,3107’ получен двойной бифуркацией и находится до ‘горизонта событий’.
‘pp4-1.9408’ обход по часовой стрелке

Фиг.17 Фазовая диаграмма траекторий циклов длины 5
Забавно, ‘pp5-1.98542’ получается из ‘pp4-1.9408’ изломом одной грани.

Фиг.18 Фазовая диаграмма траекторий циклов длины 6
‘pp6-1.77289’ получен расщеплением цикла длины 3.
‘pp6-1.99638’ получен дальнейшим изломом грани в ‘pp5-1.99638’
‘pp6-1.75488’ порождает цикл длины 3 т.к. попадает в окно с периодичностью 3, которое имеет приоритет.
Далее мы не будем смотреть на все имеющиеся циклы, с ростом периода число корней моды растёт экспоненциально, да и степени в полиномах возникают такие, что как-то становится тревожно за точность gnuplot. Просто поглядим на субъективно интересное.

Фиг.19 само-непересекающиеся циклы длины 3. 7
Эти циклы разного размера, но имеют близкую родственную связь. Заключается она в том, что всё это циклы с минимальным корнем соответствующей моды.
Аналогичный цикл длины больше 7 отловить не удалось из-за нарастающей потери точности в вычислениях.

Фиг.20 Еще одна серия траекторий с ростом длины циклов по единице.
Это, кстати, вторые снизу минимальные корни.
По-видимому, это (+1) вполне популярная история. Возможно, стоит продолжить.

Фиг.21 Третьи снизу корни мод.
В принципе логика понятна.

Фиг.22 Фазовая диаграмма траектории длины 11.
Здесь хорошо видно, как нарастает число “зубьев”, а также то, что точки фазовой диаграммы находятся на параболе, что логично, учитывая их происхождение.
Однако, и это еще не всё. Встречаются и вот такие жемчужины:

Фиг.23 цикл длины 9 — утроение цикла.
До сих пор мы встречали только удвоение циклов, например, “pp6-1.77289” из “pp3-1.755”.

Фиг.24 удвоение и утроение цикла 3.
Цикл 3 при -1.755.
Цикл 6 при -1.77289
Цикл 9 при -1.7859
Утроение (-1.7859) находится за локальным “горизонтом событий”.
И, по видимому, соответствует “циклу 3*3 за горизонтом событий цикла 3”.
Если гипотеза верна, между [-1.7859:-1.7783] мы найдём и цикл 3*6 и 3*5 … (если точности хватит)

Фиг.25 Бифуркационный “спектр” в интересующем нас интервале.
Невозможно не отметить, насколько этот кусочек спектра похож на полный спектр, приведенный выше (Фиг.7). Что еще раз указывает на фрактальную природу происходящего.

Фиг.26 Расщепление цикла 3 на 4, 5, 6 частей
И до кучи, вот так выглядит попадание мимо окна периодичности (если вообще можно попасть мимо окна периодичности), либо очень большой цикл, что в общем то одно и то же.

Фиг.27 псевдо-хаотическое поведение, длинный цикл.

Однажды для презентации мне понадобились анимированные графики. С графиками, собственно, проблем не возникло, а для их анимации пришлось воспользоваться еще одним пакетом animation , который можно установить из CRAN.
Стоит отметить, что animation в процессе обработки изображений использует пакет программ ImageMagick, так что его желательно установить заранее. Под Windows работоспособность этого решения я не проверял.
Для создания анимированного графика нам, в общем-то, понадобится всего одна функция такого вида:
Так получилось, что в то время я проходил весьма познавательный курс Introduction to Dynamical Systems and Chaos, и мне было интересно, как от относительно простых математических объектов переходят к весьма причудливым изображениям. Взять хотя бы логистическое отображение такого вида:
Эту итерационную функцию можно интерпретировать как зависимость численности популяции от ее величины в предыдущий период времени и от параметра r , который обычно называют скоростью размножения. Собственно, сама по себе функция довольно унылая и имеет весьма банальный график. Интересные вещи проявляются, если рассматривать ее бифуркационную диаграмму: изменяя параметр r , можно наблюдать «динамику» неподвижных точек уравнения. Запишем логистическое отображение в R в виде такой функции:
Зададим некоторые интересные точки и начальные параметры для отображения и построим бифуркационную диаграмму, изменяя масштаб изображения по ходу дела:
Можно заметить, что количество неподвижных точек уравнения удваивается, образуя таким образом каскад бифуркаций и проявляя фрактальную структуру. Тут еще уместно вспомнить о таком феномене, как универсальность. Рассмотрим два уравнения:


Первое уравнение определяет расстояние от одной точки бифуркации до следующей в единицах r . Второе же показывает, насколько ответвление n длиннее ответвления n+1. Так вот, оказывается, что

Число 4.669201… называется универсальной постоянной Фейгенбаума, которая как раз и характеризует скорость перехода динамических систем от порядка к детерминированному хаосу.
Другой интересный и не менее известный объект — аттрактор Лоренца. На Хабре ему даже посвящена отдельная статья. Для описания движения воздушных потоков Эдвард Лоренц использовал систему из трех обыкновенных дифференциальных уравнений, известных теперь как уравнения Лоренца:

Не будем изголяться и решим эту систему численно — методом Эйлера:
Решение системы для параметров, заданных по умолчанию, выглядит так:

Изменяя параметр r, можно получить серию изображений, на которых видно, как происходит эволюция системы от начальных условий и неподвижной точки к, собственно, странному аттрактору.
Читайте также:


