Аналитическое выравнивание в excel
Сущность этого способа заключается в том, что подбирается уравнение, которое наиболее полно отражает характер изменения динамического ряда за изучаемый период. Таким уравнением, в частности, может быть уравнение прямой линии Уt = а + bt, где Уt – выровненное по уравнению значение динамического ряда; t – продолжительность времени; а и b – параметры уравнения, которые необходимо определить. Чтобы определить параметры уравнения, надо решить систему нормальных уравнений: , которая отвечает требованию .
Особенности анализа радов динамики заключаются в расчете показателей, которые способствуют выявлению общей тенденции развития явления во времени на основе применения аналитического выравнивания рядов динамики по уравнению прямой линии:
Уt = а + bt(уравнение тренда).
Дня нахождения параметров " а" и " b" составляется табл. 6 исходных и расчетных данных.
Аналитическое выравнивание может быть проведено с использованием различных функций (линейной, показательной, логарифмической, параболы и т.д.). Выбор функции определяется характером изменения ряда динамики.
Параметры уравнения тренда могут рассчитываться упрощенным способом, если t подобрать так, чтобы сумма равнялась нулю, т.е. начало отчета перенести в середину рассматриваемого периода.
При наличии нечетного числа уровней ряда для получения средний уровень ряда ( t) принимается за ноль. Уровни ряда выше этого уровня (t=0) обозначаются порядковыми числами со знаком минус (-1,-2 и т.д.), а ниже – порядковыми числами со знаком плюс (+1,+2 и т.д.)
При наличии четного числа уровней ряда для получения уровни ряда от середины обозначаются: - вверх ( -1,-3,-5 и т.д.), -вниз (+1,+3,+5 и т.д.).
Определение тенденции развития явления
| Год | Себестоимость 1ц продукции, р. | Время отклонения | Квадрат времени | Произведение себестоимости на время | Выровненный уровень себестоимости 1ц продукции (тренд), р. |
| n | y | t | у´t | Yt | |
| -2 | -40 | 19,5+0,3´(-2)=18,9 | |||
| -1 | -15 | 19,5+0,3´(-1)=19,2 | |||
| 19,5+0,3´0=19,5 | |||||
| 19,5+0,3´1=19,8 | |||||
| 19,5+0,3´2=21,1 | |||||
| Итого |
Тогда, а= b= в нашем примере b= .
На график заносят как фактические, так и выровненные (расчетные) уровни изучаемого явления по годам, показывающие общую тенденцию развития явления (в нашем примере - изменения себестоимости 1ц продукции) (рис.3).
Основным содержанием метода аналитического выравнивания временных рядов является расчет общей тенденции развития (тренда) как функции времени:
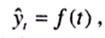
(11.7)
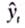
где — теоретические значения временного ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
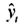
Определение теоретических (расчетных) значений производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает основную тенденцию развития временного ряда.
Простейшими моделями (формулами), выражающими тенденцию развития, являются следующие:
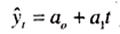
• линейная функция, график которой является прямой линией'- ;
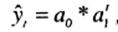
• показательная функция:
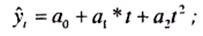
• степенная функция второго порядка (парабола):
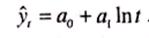
• логарифмическая функция:
Расчет параметров функции обычно производится методом наименьших квадратов (МНК), в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическим и эмпирическим уровнями:
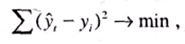
(11.8)
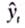
где -, — выровненные (расчетные) уровни, a yt — фактические уровни.
Выравнивание по прямой используется в тех случаях, когда абсолютные приросты практически постоянны, т.е. когда уровни изменяются в арифметической профессии (или близко к ней).
Выравнивание по показательной функции применяется, когда ряд отражает развитие в геометрической профессии, т.е. цепные коэффициенты роста практически постоянны.
Выравнивание по степенной функции (параболе второго порядка) используется, когда ряды динамики изменяются с постоянными цепными темпами прироста.
Выравнивание по логарифмической функции применяется, когда ряд отражает развитие с замедлением роста в конце периода, т.е. когда прирост в конечных уровнях временного ряда стремится к нулю.
Правильность расчетов аналитических уровней можно проверить по следующему условию: сумма значений эмпирического ряда должна совпадать с суммой вычисленных уровней выровненного ряда. При этом может возникнуть небольшая погрешность в расчетах из-за округления вычисляемых величин:

Для оценки точности трендовой модели используется коэффициент детерминации:

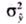
где — дисперсия теоретических данных, полученных по трендовой модели, а ст; -дисперсия эмпирических данных.
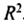
Трендовая модель адекватна изучаемому процессу и отражает тенденцию его развития при значениях , близких к 1.
После выбора наиболее адекватной модели можно сделать прогноз на любой из периодов. При составлении прогнозов оперируют не точечной, а интервальной оценкой, определяя так называемые доверительные интервалы прогноза. Величина доверительного интервала определяется в общем виде следующим образом:

Величина S; определяется по формуле:
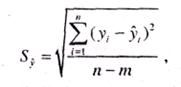
(11.12)
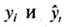
где - фактические и расчетные значения уровней динамического ряда; п —число уровней ряда; m — количество параметров в уравнении тренда (для уравнения прямой m = 2, для уравнения параболы 2-го порядка m = 3).
После необходимых расчетов определяется интервал, в котором с определенной вероятностью будет находиться прогнозируемая величина.
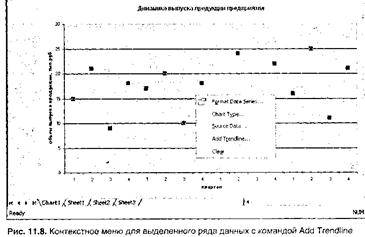
С помощью Microsoft Excel строить трендовые модели достаточно просто. Сначала эмпирический временной ряд следует представить в виде диаграммы одного из следующих типов: гистограмма, линейчатая диаграмма, график, точечная диаграмма, диаграмма с областями, а затем щелкнуть на диаграмме правой кнопкой мыши на одном из маркеров данных. В результате на диаграмме будет выделен сам временной ряд, а на экране раскроется контекстное меню, как показано на рис. 11.8. В этом меню следует выбрать команду Add Trendline (Добавить линию тренда). На экран будет выведено диалоговое окно Add Trendline, как показано на рис. 11.9.

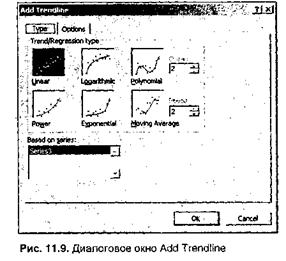
На вкладке Туре (Тип) этого диалогового окна выбирается требуемый тип тренда:
• полиномиальный, от 2-й до 6-й степени включительно (Polinomial);
• скользящее среднее, с указанием периода сглаживания от 2 до 15 (Moving Average).
На вкладке Options (Параметры) этого диалогового окна, показанной на рис. 11.10, задаются дополнительные параметры тренда.
1. Trendline Name (Название сглаженной кривой) — в этой группе выбирается название, которое будет выведено на диаграмму для обозначения функции, использованной для сглаживания временного ряда. Возможны следующие варианты:
Automatic (Автоматическое) — при установке переключателя в это положение Microsoft Excel автоматически формирует название функции сглаживания тренда, основываясь на выбранном типе тренда, например Linear (Линейная функция).
Custom (Другое) — при установке переключателя в данное положение в поле справа можно ввести собственное название для функции тренда, длиной до 256 символов.
2. Forecast (Прогноз) — в этой группе можно указать, на сколько периодов вперед (поле Forward) требуется спроектировать линию тренда в будущее и на сколько периодов назад (поле Backward) следует спроектировать линию тренда в прошлое (эти поля недоступны в режиме скользящего среднего).
3. Set intercept (Пересечение кривой с осью Y в точке) — этот флажок опции и расположенное справа поле ввода позволяют непосредственно указать точку, в которой линия тренда должна пересекать ось Y (эти поля доступны не для всех режимов).
4. Display equation on chart (Показывать уравнение ка диаграмме) — при установке этого флажка опции на диаграмму будет выведено уравнение, описывающее сглаживающую линию тренда.
5. Display R-squared value on chart (Поместить на диаграмму величину достоверности аппроксимации R-) — при установке данного флажка опции на диаграмме будет показано значение коэффициента детерминации.
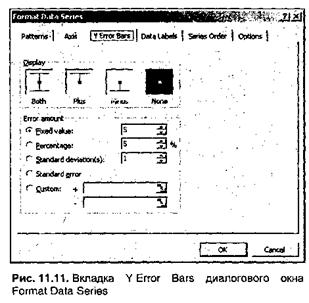
Вместе с линией тренда на графике временного ряда могут быть также изображены планки погрешностей. Для вставки планок погрешностей необходимо выделить ряд данных, щелкнуть на нем правой кнопкой мыши и выбрать в раскрывшемся контекстном меню команду Format Data Series (рис. 11.8). На экране раскроется диалоговое но Format Data Series (Формат ряда данных), в котором следует перейти на вкладку Error Bars (Y-погрешности), показанную на рис. 11.11.
На этой вкладке с помощью переключателя Error amount (Величина погрешности) выбирается тип планок и вариант их расчета в зависимости от вида погрешности.
• Fixed value (Фиксированное значение) — при установке переключателя в это положение за допустимую величину ошибки принимается заданное в поле счетчика справа постоянное значение;
• Percentage (Относительное значение) — при установке переключателя в данное положение для каждой точки данных вычисляется допустимое отклонение, исходя из заданного в поле счетчика справа значения процента;

• Standard deviation(s) (Стандартное отклонение) — при установке переключателя в данное положение для каждой точки данных вычисляется стандартное отклонение, которое затем умножается на заданное в поле счетчика справа число (коэффициент кратности);
• Standard error (Стандартная погрешность) — при установке переключателя в данное положение принимается стандартная величина ошибки, постоянная для всех элементов данных;
• Custom (Пользовательская) — при установке переключателя в это положение вводится произвольный массив значений отклонений в положительную и/или отрицательную сторону (можно ввести ссылки на диапазон ячеек).
Планки погрешностей тоже можно форматировать. Для этого их следует выделить щелчком правой кнопки мыши и выбрать в раскрывшемся контекстном меню команду Format Error Bars (Формат планок погрешностей).
Рассмотрим конкретный пример — пусть требуется построить модель тренда для исходных данных, представленных на рис. 11.2. Вначале представим этот временной ряд в виде графика, построенного с помощью мастера диаграмм (см. рис. 11.8). Для нахождения наиболее подходящего случаю уравнения тренда воспользуемся командой Add Trendline. Результаты подбора уравнения приведены в табл. 11.2.

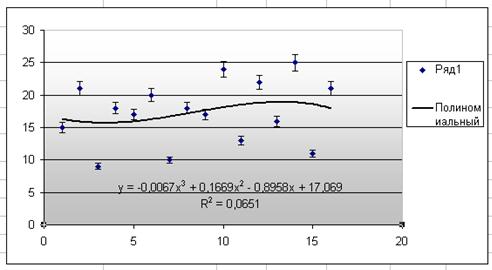
Принимая во внимание результаты выполненного в Excel аналитического выравнивания (см. табл. 11.2), в качестве математической модели тренда выбирается полином 3-го порядка (при подборе уравнения не рассматривались полиномы выше третьего порядка). Выбранная модель тренда графически представлена на рис. 11.12.
Резюме
В данной главе были рассмотрены основные характеристики временного ряда, модели декомпозиции временного ряда, а также основные методы сглаживания ряда -метод скользящего среднего, экспоненциального сглаживания и аналитического выравнивания. Для решения этих задач Microsoft Excel предлагаются такие инструменты, как Moving Average (Скользящее среднее) и Exponential Smoothing (Экспоненциальное сглаживание), которые позволяют сглаживать уровни эмпирического временного ряда, а также команда Add Trendline (Добавить линию тренда), которая позволяет строить модели тренда и делать прогноз на основе имеющихся значений временного ряда.
1. При анализе тренда для некоторого набора данных коэффициент детерминации для линейной модели оказался равен 0,95, для логарифмической — 0,8, а для полинома третьей степени — 0,9636. Какая трендовая модель наиболее адекватна изучаемому процессу:
в) полином 3-й степени.
2. Поданным, представленным на рис. 11.2, спрогнозируйте объем выпуска продукции в 2003 году. Какая общая тенденция поведения исследуемой величины следует из результатов вашего прогноза:

Аналитическое выравниваниеосновано на том, что уровни ряда динамики выражаются в виде функции времени. Функцию выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.
При выравнивании обычно используются следующие зависимости: линейная, параболическая, гиперболическая, экспоненциальная [1].
Чтобы выявить тенденцию уровня урожайности в рядах динамики с использованием ППП Excel, необходимо ввести данные в Excel. По этим данным построить графики и линии тренда к этим графикам.
Таблица 1 – Выравнивание ряда динамики аналитическим методом по линейной функции
Урожайность подсолнечника, ц с 1 га
Порядковый номер года
Рисунок 1 – Выравнивание ряда динамики аналитическим методом по линейной функции
По выравниванию ряда динамики аналитическим методом по линейной функции видно, что урожайность картофеля за 1991-2017 года, а также в прогнозируемых 2018 и 2019 годах, имеет тенденцию к росту, несмотря на резкие спады урожайности в 1998,1999 и 2010 годах. В 2018 году расчетное значение показателя урожайности картофеля составит 152,9 ц с 1 га, а в 2019 году расчетное значение показателя урожайности картофеля составит 154,98 ц с 1 га.
Таблица 2 – Выравнивание ряда динамики аналитическим методом по логарифмической функции
Урожайность подсолнечника, ц с 1 га
Порядковый номер года,
Рисунок 2 – Выравнивание ряда динамики аналитическим методом по логарифмической функции
По выравниванию ряда динамики аналитическим методом по логарифмической функции видно, что урожайность картофеля за 1991-2017 года, а также в прогнозируемых 2018 и 2019 годах, имеет тенденцию к росту, несмотря на резкие спады урожайности в 1998,1999 и 2010 годах.
Таблица 3 – Выравнивание ряда динамики аналитическим методом по полиномиальной функции
Урожайность подсолнечника, ц с 1 га
Порядковый номер года,
Рисунок 3 – Выравнивание ряда динамики аналитическим методом по полиномиальной функции
По выравниванию ряда динамики аналитическим методом по полиномиальной функции видно, что урожайность картофеля за 1991-2017 года, а также в прогнозируемых 2018 и 2019 годах, имеет тенденцию к росту, несмотря на резкие спады урожайности в 1998,1999 и 2010 годах.
Список литературы
1. Аблеева, А. М. Статистика [Электронный ресурс] : учебное пособие / А. М. Аблеева ; М-во сел. хоз-ва РФ, Башкирский ГАУ. - Уфа, 2018.- 173 с.
Читайте также:


