Sin в полярных координатах
Онлайн калькулятор поможет вычислить площадь фигуры в полярных координатах, Вам пригодятся навыки построения графиков функций в полярной системе координат.
Синтаксис
основных функций:
x a : x^a
|x| : abs(x)
√x : Sqrt[x]
n √x : x^(1/n)
a x : a^x
log a x : Log[a, x]
ln x : Log[x]
cos x : cos[x] или Cos[x]
sin x : sin[x] или Sin[x]
tg : tan[x] или Tan[x]
ctg : cot[x] или Cot[x]
sec x : sec[x] или Sec[x]
cosec x : csc[x] или Csc[x]
arccos x : ArcCos[x]
arcsin x : ArcSin[x]
arctg x : ArcTan[x]
arcctg x : ArcCot[x]
arcsec x : ArcSec[x]
arccosec x : ArcCsc[x]
ch x : cosh[x] или Cosh[x]
sh x : sinh[x] или Sinh[x]
th x : tanh[x] или Tanh[x]
cth x : coth[x] или Coth[x]
sech x : sech[x] или Sech[x]
cosech x : csch[x] или Csch[е]
areach x : ArcCosh[x]
areash x : ArcSinh[x]
areath x : ArcTanh[x]
areacth x : ArcCoth[x]
areasech x : ArcSech[x]
areacosech x : ArcCsch[x]
конъюнкция "И" ∧ : &&
дизъюнкция "ИЛИ" ∨ : ||
отрицание "НЕ" ¬ : !
импликация =>
число π pi : Pi
число e : E
бесконечность ∞ : Infinity, inf или oo
Построим график функции в полярных координатах r=r(φ),
где 0 <= φ <= 2π,
но вы можете задать свои границы φ.
Задайте также полярную функцию r(φ).
Примеры кривых
| Название кривой | Уравнение |
|---|---|
| Окружность | |
| Спираль Архимеда | |
| Кардиоида | |
| Улитка Паскаля | |
| Парабола | |
| Полярная роза | |
| Бабочка | |
| Сердце |
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке): absolute(x) Абсолютное значение x(модуль x или |x|) arccos(x) Функция - арккосинус от x arccosh(x) Арккосинус гиперболический от x arcsin(x) Арксинус от x arcsinh(x) Арксинус гиперболический от x arctg(x) Функция - арктангенс от x arctgh(x) Арктангенс гиперболический от x exp(x) Функция - экспонента от x (что и e^x) log(x) or ln(x) Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) sin(x) Функция - Синус от x cos(x) Функция - Косинус от x sinh(x) Функция - Синус гиперболический от x cosh(x) Функция - Косинус гиперболический от x sqrt(x) Функция - квадратный корень из x sqr(x) или x^2 Функция - Квадрат x ctg(x) Функция - Котангенс от x arcctg(x) Функция - Арккотангенс от x arcctgh(x) Функция - Гиперболический арккотангенс от x tg(x) Функция - Тангенс от x tgh(x) Функция - Тангенс гиперболический от x cbrt(x) Функция - кубический корень из x gamma(x) Гамма-функция LambertW(x) Функция Ламберта x! или factorial(x) Факториал от x В выражениях можно применять следующие операции: Действительные числа вводить в виде 7.5, не 7,5 2*x - умножение 3/x - деление x^3 - возведение в степень x + 7 - сложение x - 6 - вычитание 15/7 - дробь
Другие функции: asec(x) Функция - арксеканс от x acsc(x) Функция - арккосеканс от x sec(x) Функция - секанс от x csc(x) Функция - косеканс от x floor(x) Функция - округление x в меньшую сторону (пример floor(4.5)==4.0) ceiling(x) Функция - округление x в большую сторону (пример ceiling(4.5)==5.0) sign(x) Функция - Знак x erf(x) Функция ошибок (или интеграл вероятности) laplace(x) Функция Лапласа asech(x) Функция - гиперболический арксеканс от x csch(x) Функция - гиперболический косеканс от x sech(x) Функция - гиперболический секанс от x acsch(x) Функция - гиперболический арккосеканс от x
Постоянные: pi Число "Пи", которое примерно равно
3.14159.. e Число e - основание натурального логарифма, примерно равно
2,7183.. i Комплексная единица oo Символ бесконечности - знак для бесконечности
На предыдущем уроке мы познакомились с полярными координатами, а также научились строить отдельно взятые точки и распространённые кривые в данной системе координат. Давайте подведём краткие промежуточные итоги и ответим на важный вопрос:
как построить линию в полярной системе координат?
– Сначала необходимо отметить полюс, изобразить полярную ось и указать масштаб. Кроме того, на первоначальном этапе желательно найти область определения функции, чтобы сразу же исключить из рассмотрения лишние угловые значения.
– В большинстве случаев потребуется найти десяток-другой точек, принадлежащих линии. Но иногда можно обойтись меньшим количеством, а то и вовсе отделаться схематическим чертежом.
– На следующем шаге следует прочертить угловые направления и отметить найденные точки. Как это сделать с помощью каменного топора транспортира, циркуля и линейки, я подробнейшим образом объяснил в начале статьи о полярных координатах.
– И, наконец, отложенные точки нужно аккуратно-аккуратно соединить линией (линиями).
Отработаем алгоритм построения на более основательных типовых задачах:
Построить по точкам линию, заданную в полярной системе координат уравнением , рассматривая значения угла с интервалом в рад. Найти уравнение линии в прямоугольной системе координат.
Решение: найдём область определения. Поскольку полярный радиус неотрицателен, то:
Очевидно, что условие выполнено для любого значения «фи», но, тем не менее, расскажу об удобном графическом способе решения тригонометрического неравенства: изобразите на черновике (или представьте мысленно) график функции левой части неравеснтва и прямую правой части неравенства. Непосредственно по чертежу видно, что синусоида расположена не ниже прямой , а значит, неравенство выполнено для любого значения «икс».
Итак, на угол не наложено никаких ограничений, и нам предстоит «перепахать» весь круг от 0 до , причём, по условию сделать это требуется строго с интервалом в рад. (22,5 градусов). Ложку в зубы, калькулятор в руки:
и так далее, пока не будет пройден весь оборот до «двух пи».
На практике обычно не расписывают подробные вычисления, а сразу заносят результаты в таблицу:
Рекомендую использовать мой расчётный макет, созданный в MS Excel, который позволит буквально в пару щелчков вычислить все значения «эр», сэкономив целый вагон времени. Программу можно раздобыть на странице Математические формулы и таблицы. Особо нетерпеливым читателям предлагаю также воспользоваться handmade-продуктом и быстро начертить заготовку, ориентируясь по клеточкам:
Углы проставлены для удобства и на чистовике, понятно, их записывать не надо.
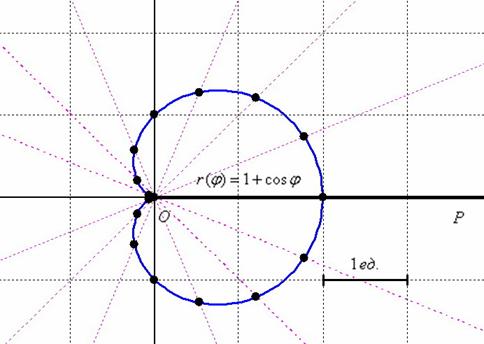
После ностальгических воспоминаний отметим найденные точки на чертеже и аккуратно соединим их линией:
Напоминаю, что одинаковые значения радиуса эффективнее засекать циркулем, а слишком малые значения для углов допустимо отметить и «на глазок».
Найдём уравнение линии в декартовой системе координат. Для этого используем тоже уже знакомый приём – домножим обе части уравнения на «эр»:
Перенесём «икс» налево и возведём обе части в квадрат:
Дальнейшее возведение левой части в квадрат только усложнит запись, поэтому результат целесообразнее оставить в таком виде.
Из полученного уравнения следует, что кардиоида – это алгебраическая линия 4-го порядка, обратите внимание, насколько сложной получилась её формула по сравнению с полярной системой координат. Алгебраическим линиям 3-го, 4-го, 5-го, 6-го и высших порядков посвящены серьёзные исследования, и грибники без труда могут отыскать море информации по данной теме. Ну а я, как обычно, предлагаю вкусную и здоровую пищу на каждый день:
Линия задана уравнением в полярной системе координат. Требуется:
1) построить линию по точкам, придавая значения через интервал , начиная с и заканчивая ;
2) найти уравнение линии в декартовой системе координат;
3) определить вид кривой.
Типовая формулировка, предвещающая час (а то и больше) усердного пыхтения, а нередко и чертыханья студента. Но только не того, кто прочитал эту и предыдущую статью о полярных координатах! Примерный образец оформления задачи в конце урока.
Рассмотрим ещё ряд важных особенностей решения:
Линия задана уравнением в полярной системе координат. Требуется:
1) построить линию по точкам, начиная от до и придавая значения через промежуток ;
2) найти уравнение данной линии в прямоугольной системе координат;
3) назвать линию, найти координаты фокусов и эксцентриситет.
Решение: найдём область определения:
Заметьте, что ноль в знаменателе нас тоже не устраивает, поэтому неравенство становится строгим. Перенесём косинус направо и развернём избушку к лесу задом:
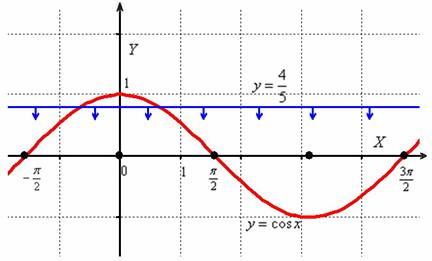
Неравенство несложно решить аналитически, но для лучшего понимания я опять воспользуюсь графическим методом. Изобразим на черновике или представим мысленно графики функций , при этом нас будет интересовать только один период – от до . Условию удовлетворяет та часть синусоиды, которая расположена ПОД прямой :
То есть, в нашем распоряжении оказываются почти все значения угла за исключением макушки, расположенной на симметричном отрезке .
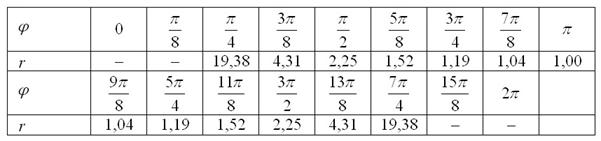
Таким образом, . Арккосинус составляет примерно 37 градусов, поэтому из рассмотрения исключаем углы и . Заполним расчётную таблицу с прочерками в соответствующих ячейках:
Чайники могут, в принципе, вообще не загружаться областью определения и ставить тире по факту: получилось отрицательное значение «эр» – поставили.
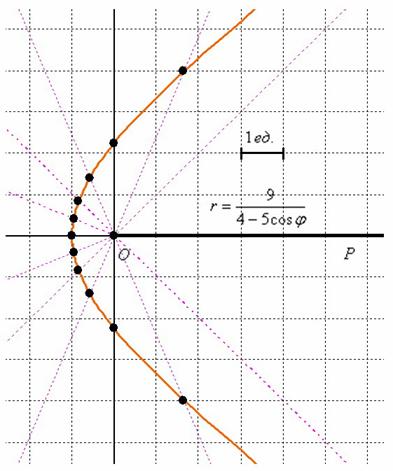
Выполним чертёж:
На него не вместились точки, соответствующие значениям , но не уменьшать же из-за этого масштаб. Сойдёт и так.
2) Найдём уравнение линии в прямоугольной системе координат. По всем признаком должна получиться гипербола.
Избавляемся от дроби:
Используем формулы перехода :
Дальнейшие действия хорошо знакомы из практикума Задачи с линиями 2-го порядка:
3) Данная линия представляется собой гиперболу с центром в точке , действительной полуосью , мнимой полуосью . Впрочем, формально по условию можно было и не упоминать о деталях.
Вы спросите: «но в полярной же системе координат прорисовалась только одна ветвь гиперболы, поэтому не ошибочно ли говорить о целой гиперболе?». Не ошибочно!
И вот по какой причине: если подразумевать обобщённую полярную систему координат с отрицательными значениями «эр», то при значениях угла из интервала прорисуется левая ветвь! Желающие могут провести самостоятельную проверку и анализ этого факта. Я не сторонник и даже противник обобщенных полярных координат, но в данном случае всё получается ловко и чертовски удобно – можно как бы и не оговариваться о том, что на чертеже только одна ветвь гиперболы.
Вычислим координаты фокусов и эксцентриситет. По условию уравнение не нужно приводить к каноническому виду, а значит, требуемые вещи проще найти напрямую – с учётом параллельного переноса гиперболы, к тому же, она не повёрнута.
Вычислим значение и поправкой на параллельный перенос в точку найдём фокусы:
Педантичные люди могут ещё записать развёрнутый ответ.
Заключительное задание для самостоятельного решения:
Линия задана уравнением в полярной системе координат. Требуется:
1) построить линию по точкам, начиная от до и придавая значения через промежуток ;
2) найти уравнение данной линии в прямоугольной системе координат и определить её вид.
3) Привести уравнение к каноническому виду и выполнить чертёж в прямоугольной системе координат. Найти фокусы кривой и её эксцентриситет.
Внимательно проанализируйте, что и в каком порядке требуется выполнить по условию. Сам много раз налетал – краем глаза показалось одно, а нужно совсем другое. В образце решения приведение уравнения линии 2-го порядка к каноническому виду выполнено академическим способом.
На основе полярных координат плоскости базируются цилиндрические и сферические координаты пространства. В частности, угловые величины широко используются в навигации (не зря упоминались лётчики и самолёты) и астрономии. Действительно, представьте земной шар (а если строго, эллипсоид), эллиптические орбиты планет и вы поймёте, что распиаренная прямоугольная система координат как-то здесь совсем не в тему. Ну а мне пора плотно прикрыть дверь аналитической геометрии и вернуться к матанализу, где полярные координаты тоже эксплуатируются на полную катушку.
До скорых встреч!
Решения и ответы:
Пример 7: Решение: 1) Найдём область определения функции:
– любое.
Заполним таблицу требуемыми значениями угла и соответствующими значениями полярного радиуса:
Выполним чертёж:
2) Найдём уравнение линии в декартовой системе координат:
Используем формулы :
– уравнение линии в прямоугольной системе координат.
3) Данная кривая представляет собой эллипс с центром симметрии в точке , большой полуосью и малой полуосью .
Пример 9: Решение: 1) Найдём область определения функции:
Заполним расчётную таблицу:
Выполним чертёж:
2) Найдём уравнение линии в декартовой системе координат:
Используем формулы :
– искомое уравнение. Это парабола.
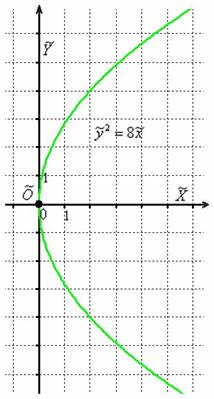
3) Приведём уравнение линии к каноническому виду с помощью перехода к новой системе координат , которая получается путём поворота исходной системы координат на рад. вокруг точки и её параллельным переносом центром в точку (координаты – в старой системе координат).
В результате получено каноническое уравнение параболы , фокальный параметр которой равен . Выполним чертёж:
Найдём фокус: .
Эксцентриситет любой параболы равен единице.
Автор: Емелин Александр
(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам
Данный калькулятор поможет построить график и кривые на плоскости в полярных координатах.
Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом.
Полярная система координат задаётся лучом, который называют нулевым лучом, или полярной осью. Точка, из которой выходит этот луч, называется началом координат, или полюсом.
Примеры уравнений кривых в полярных координатах:
R=2*(1-cos theta) - кардиоида;
R=2*sin(4*theta) - полярная роза;
R=2+sin(3* theta) - трохоида;
R=9/(4-5*cos theta) - гипербола.
Синтаксис
основных функций:
x a : x^a
|x| : abs(x)
√x : Sqrt[x]
n √x : x^(1/n)
a x : a^x
log a x : Log[a, x]
ln x : Log[x]
cos x : cos[x] или Cos[x]
sin x : sin[x] или Sin[x]
tg : tan[x] или Tan[x]
ctg : cot[x] или Cot[x]
sec x : sec[x] или Sec[x]
cosec x : csc[x] или Csc[x]
arccos x : ArcCos[x]
arcsin x : ArcSin[x]
arctg x : ArcTan[x]
arcctg x : ArcCot[x]
arcsec x : ArcSec[x]
arccosec x : ArcCsc[x]
ch x : cosh[x] или Cosh[x]
sh x : sinh[x] или Sinh[x]
th x : tanh[x] или Tanh[x]
cth x : coth[x] или Coth[x]
sech x : sech[x] или Sech[x]
cosech x : csch[x] или Csch[е]
areach x : ArcCosh[x]
areash x : ArcSinh[x]
areath x : ArcTanh[x]
areacth x : ArcCoth[x]
areasech x : ArcSech[x]
areacosech x : ArcCsch[x]
конъюнкция "И" ∧ : &&
дизъюнкция "ИЛИ" ∨ : ||
отрицание "НЕ" ¬ : !
импликация =>
число π pi : Pi
число e : E
бесконечность ∞ : Infinity, inf или oo
Закончим бой с двойным интегралом нокаутом в третьем раунде. Что нужно знать и уметь для полной победы? Ещё раз взглянем на заголовок статьи… очевидно, вы должны знать, что такое полярные координаты… и уметь решать двойные интегралы =) Стоп-стоп, не закрываем в панике страницу – первое осваивается в считанные минуты, ну а второе, конечно, несколько дольше. Итак, чайникам – двойные интегралы для чайников, остальных же читателей приглашаю ознакомиться с третьим уроком темы. Новизны будет совсем немного и если вы мало-мальски набили руку на вычислении двойных интегралов, то особых трудностей возникнуть не должно.
Типовое задание формулируется примерно так: «Вычислить двойной интеграл, используя полярную систему координат». После чего для решения предлагается … обычный двойной интеграл в декартовых координатах по области . Сначала рассмотрим более простой и распространённый случай, когда подынтегральная функция двух переменных и двойной интеграл численно равен площади области интегрирования. Разберём алгоритм решения на бесхитростной демо-задаче:
Вычислить площадь плоской фигуры, ограниченную линиями , с помощью двойного интеграла, используя полярную систему координат
Решение: На первом этапе ничего нового. Выполняем чертёж области в прямоугольной системе координат. Линейное неравенство определяет правую полуплоскость, включая ось , а уравнение , очевидно, задаёт какую-то линию 2-го порядка. Чтобы выяснить, какую именно – выделим полный квадрат:
– окружность единичного радиуса с центром в точке .
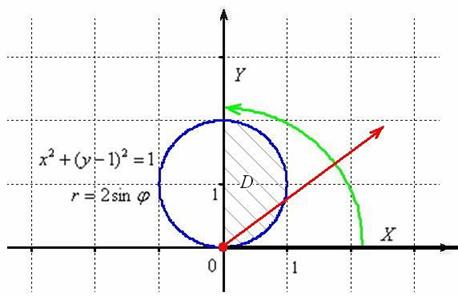
Таким образом, требуется вычислить площадь половинки круга:
Не упустим возможность сразу узнать ответ. По школьной формуле у нас должно получиться:
Площадь фигуры стандартно рассчитывается по формуле , однако по условию нужно воспользоваться полярными координатами. На всякий случай закомментирую расположение полярной системы координат: полюс совпадает с началом прямоугольной системы, а полярная ось – с положительным направлением оси . Полярную ось можно прочертить жирнее, но лично я часто этим пренебрегаю.
При переходе к полярной системе координат произведение дифференциалов ВСЕГДА превращается в следующую вещь:
То есть, от интегрирования по декартовым «иксу» и «игреку» мы перешли к интегрированию по полярному радиусу «эр» и полярному углу «фи». Обратите внимание на дополнительно появившийся множитель , образно говоря, это «плата за переход», любители высшей математики могут погуглить якобиан перехода к полярным координатам. Практическая же сторона вопроса состоит в том, что этот множитель «эр» терять нельзя.
Но это ещё не всё – ведь границы области тоже заданы в декартовой системе. Используем формулы перехода к полярным координатам . Ось ординат не трогаем, а вот окружность потревожим:
– получено типовое уравнение, на котором заострялось внимание ещё в статье Полярные координаты.
Теперь двойной интеграл необходимо свести к повторным интегралам. Для этого нужно выяснить порядок обхода области. На уроке Двойные интегралы для чайников мы орудовали виртуальной лазерной указкой, в полярных же координатах более удачна другая ассоциация – просвечивание области радаром. Представьте, что из точки полюса исходит луч света и вращается против часовой стрелки.
Когда луч радара поворачивается от полярной оси до угла (зелёная стрелка), то он входит в область непосредственно из полюса (начиная со значения ) и выходит из неё через окружность (красная стрелка). Таким образом, на промежутке полярный радиус изменяется в пределах и область интегрирования полностью «просканирована».
Множитель , разумеется, уходит во внутренний интеграл, где осуществляется интегрирование по «эр».
Начинающим вновь рекомендую оформить концовку в два пункта:
1) , чтобы продемонстрировать на следующем шаге примечательный факт, дальше упрощать пока не буду.
2) Подставляем трофей во внешний интеграл:
Заметьте, что здесь прорисовалась знакомая формула площади криволинейного сектора , которой мы активно пользовались на уроке Вычисление площади в полярных координатах с помощью интеграла, и фактически 2-й пункт – это повторение пройденного материала!
Что и требовалось получить.
Ответ:
В простых случаях, как этот, вычисления можно оформить и одной строкой:
Но злоупотреблять короткой дорожкой не советую – повышается риск запутаться.
В разобранной задаче жёстко требовалось использовать полярную систему координат, и это очень хорошо! Я не иронизирую. Как ни странно, более свободная формулировка условия может здОрово осложнить жизнь. Отрубим ящерице хвост:
«Вычислить площадь плоской фигуры, ограниченную линиями , с помощью двойного интеграла»
Дело в том, что площадь данной фигуры рассчитывается и с помощью двойного интеграла в прямоугольной системе координат. Но решение получается длительным и громоздим (см. задачу нахождения площади круга), и если человек не знает о возможности перехода к полярным координатам (а по условию это не запрещено!), то будет загружен трудной работой.
Давайте ещё укоротим условие:
«Вычислить площадь плоской фигуры, ограниченную линиями »
Здесь появилась новая степень свободы, и площадь фигуры помимо прочих способов можно рассчитать с помощью однократного интеграла (решение будет почти совпадать с решением через двойной интеграл). А люди со своеобразным чувством юмора вычислят площадь и по школьной формуле, чтобы затем настойчиво доказывать рецензенту корректность своего решения =) В чём, кстати, будут правы – ибо поборник конкретики должен и задачи ставить конкретно!
Чуть позже я коснусь ещё одной важной разновидности условия, а пока рассмотрим более содержательное задание:
С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями .
Решение: Изобразим данную фигуру на чертеже. С прямыми всё понятно, осталось прояснить вид линий 2-го порядка. Выделяем полные квадраты:
– окружность единичного радиуса с центром в точке .
– окружность с центром в точке радиуса 2.
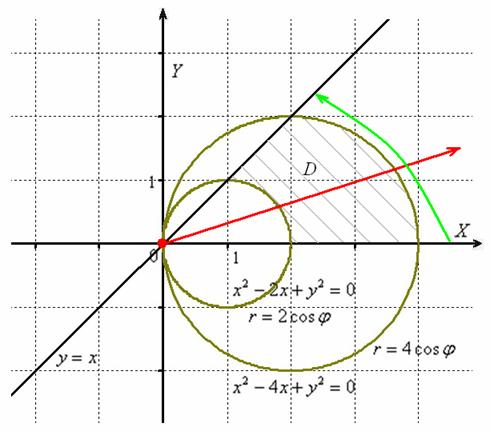
Таким образом:
В условии задачи ничего не сказано о полярной системе координат, и поэтому площадь фигуры можно рассчитать «обычным» двойным интегралом. Но что-то не хочется. Впрочем, если найдётся энтузиаст и отправит мне разборчивое решение, то я его, пожалуй, опубликую в качестве страшилки =)
Какова предпосылка для перехода к полярным координатам?
Очевидно, что основной предпосылкой является наличие окружности (ей). Подчёркиваю, что это лишь предпосылка, а не обязательное правило! То есть, область интегрирования может быть ограничена окружностью (ями), но переход к полярным координатам только усложнит решение, а то и вообще заведёт его в тупик. И такие примеры встречаются реально.
Итак, площадь фигуры вычислим с помощью двойного интеграла, используя полярную систему координат:
По формулам перехода найдём полярные уравнения окружностей:
Теперь выясним порядок обхода области. Луч радара входит в область через окружность и выходит из неё через окружность (красная стрелка), при этом он осуществляет поворот от полярной оси до угла (зелёная стрелка).
Напомню также, что «альфа» и «бета» – это не просто формальные значения углов: полярное уравнение непосредственно задаёт полярную ось (положительное направление оси абсцисс), а уравнение – луч, исходящий из полюса и совпадающий с верхней частью прямой .
Примечание: если рассматривать обобщенные полярные координаты, то уравнение определяет полярную ось и её продолжение (всю ось абсцисс), а уравнение – всю прямую
В рассматриваемой задаче дана «хорошая» прямая и значение угла понятно «с ходу». Как найти угол в общем случае? Из материалов статьи Прямая на плоскости вспоминаем, что угловой коэффициент прямой равен тангенсу угла наклона данной прямой к положительному направлению оси абсцисс: . В данном случае , откуда следует, что (если тяжко с числами – тригонометрические таблицы в помощь).
Возвращаемся к решению. По результатам «сканирования» области мы выяснили, что на промежутке полярный радиус изменяется в пределах .
Перейдём к повторным интегралам:
Остальное – дело техники:
Ответ:
Прикинув по чертежу количество клеточек, приходим к выводу, что полученный результат вполне и вполне правдоподобен.
Следующие два примера для самостоятельного решения:
С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями
Вычислить двойной интеграл, используя полярные координаты
В примере № 4 мы встретили ещё одну распространённую формулировку условия, в которой предложено непосредственно вычислить двойной интеграл. Да, он численно равен площади области , но, коль скоро, о площади изначально молчок, то и в решении об этом не нужно упоминать ;-) Подумайте, как грамотно записать ответ задания.
Примерные образцы решений и чертежи в конце урока. Я их оформил в разном стиле, выбирайте, что больше нравится.
То были заезженные типовики, а сейчас на очереди более редкий, но очень интересный и поучительный экземпляр:
Вычислить двойной интеграл
Решение: определённый интеграл задаёт площадь области интегрирования, но о площади нас никто не спрашивал, поэтому никого не будем загружать своей эрудицией =) К тому же она сейчас ой как потребуется для других целей.
В чём заключается особенность этого задания? Прежде всего, бросается в глаза, что область «дэ» ограничена единственной кривой, и по характерным признакам – это какая-то алгебраическая линия 4-го порядка. Основная проблема у нас с чертежом. Конечно, можно погрузиться в справочники, но на это нет ни времени, ни особого желания. Поэтому мы попытаемся ограничиться общим анализом и обойтись совсем без чертежа.
Можно ли обойтись без чертежа?
Об этом я уже говорил на 1-м уроке: если условие задачи его не требует – то можно. Правда, область интегрирования всё равно придётся представить мысленно. Но даже если у вас есть такие способности, то демонстрировать их совсем не обязательно – потому что тяжелА жизнь вундеркинда =) И житейская мудрость заключается в том, что чертёжи, по возможности лучше выполнять. Однако у нас другой случай, когда наоборот – будет подозрительно смотреться построенный график линии 4-го порядка. Знаниями убивать тоже никого не надо, и в этой связи мы постараемся отделаться чисто аналитическим решением.
Поскольку область интегрирования, как правило, ограничена, то уравнение задаёт либо единственную замкнутую кривую, либо несколько ограниченных областей – что-то наподобие лепестков полярной розы. Ситуацию помогла бы прояснить область определения функции, но её нахождение тоже затруднено ввиду навороченности уравнения.
Что делать? Подумать о возможности использования полярной системы координат. Причём подумать самостоятельно – условие нам совершенно не намекает на способ решения. Поскольку в уравнении присутствуют знакомые «икс квадрат» и «игрек квадрат», то применение полярных координат действительно выглядит перспективно. По формулам перехода :
Вот и первое достижение – удалось понизить степень. С извлечением корня никаких шероховатостей, полярный радиус неотрицателен, параметр , косинус в знаменателе – в чётной степени:
Теперь займёмся областью определения. Поскольку тригонометрические функции периодичны, то нас интересует промежуток , или, что то же самое .
Знаменатель не может равняться нулю, поэтому .
Кроме того, подкоренное выражение должно быть неотрицательным: . Сведём данное условие к простейшему тригонометрическому неравенству, применив формулы понижения степени:
Я неоднократно ратовал за графическое решение подобных неравенств, но раз уж решили обойтись без чертежей, давайте вытащим из школьного учебника известную формулу. Решением неравенства , где , является следующее множество промежутков:
, где (любое целое число).
Разделим все части неравенства на 2:
В «сферу наших интересов» входят следующие значения «ка»:
В результате, область определения полярной функции :
Два нижних значения не вошли в найденные выше промежутки, что избавляет нас от дополнительных хлопот. На отрезках расположены две одинаковые (в силу периодичности и ) кривые, и график функции , судя по всему, представляет собой что-то вроде двух одинаковых лепестков, как, собственно, и предполагалось.
Таким образом, достаточно рассмотреть промежуток , а результат удвоить. Луч радара, исходя из полюса , сразу попадает в область интегрирования и выходит из неё через границу «лепестка» ; при этом он осуществляет поворот от значения до .
Переход к повторным интегралам, думаю, всем понятен:
1) Понеслась нелёгкая:
2) Подставляем результат предыдущего пункта во внешний интеграл, не забывая про «двойку» перед ним (удвоение «лепестка»):
На первом шаге удвоили интеграл от чётной функции по симметричному относительно нуля отрезку. Чтобы «не таскать всё за собой», подынтегральную функцию удобно преобразовать отдельно. Приведём её к пригодному (и выгодному!) для интегрирования виду:
Если где-то возникли непонятки, посмотрите тригонометрические формулы. А если появились вопросы по самим принципам решения подобных интегралов, пожалуйста, посетите уроки Интегралы от тригонометрических функций и Сложные интегралы.
Ответ:
Именно так. Не забываем, что в условии не спрашивалось о площадях и квадратных единицах. Однако после того как я нашёл в своих закромах этот трудный пример и включил его в содержание статьи, мне стало жутко интересно, так как же всё-таки выглядит график функции , и не допущена ли ошибка в вычислениях. Придав параметру значение , я изобразил график функции с помощью своего графопостроителя (см. Математические формулы и таблицы), и полученное значение площади оказалось очень похоже на правду. Желающие могут проделать то же самое. А если условие подобной задачи требует чертежа – то придётся =)
Получился такой увлекательный разбор решения, что на этом фоне как-то затерялся тот момент, что в двойном интеграле может оказаться «настоящая» функция с «живым» «иксом» и/или «игреком»:
Вычислить двойной интеграл, используя полярные координаты
Решение: область интегрирования здесь очень простая – это часть кольца между концентрическими окружностями , которая располагается в четвёртой координатной четверти (о чём нам сообщают неравенства ). И коль скоро так всё просто, можно сразу заняться переходом к полярной системе координат по формулам .
Найдём уравнения окружностей:
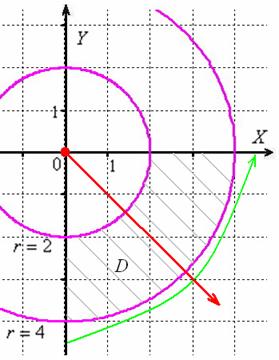
И выполним чертёж:
Порядок обхода области предельно понятен:
Можно было взять промежуток , но работать с табличным значением гораздо привычнее.
Отличие от предыдущих примеров состоит в дополнительном шаге – преобразовании подынтегральной функции . Используем те же стандартные формулы перехода . Если совсем просто, то в функцию двух переменных вместо «икс» подставляем и вместо «игрек» :
После подстановки максимально упрощаем выражение, но здесь этого особо не потребовалось.
Фишка последнего шага должна быть вам хорошо знакома: когда проводится интегрирование по переменной «эр», то переменная «фи» считается константой (и наоборот). Поэтому константу целесообразно сразу вынести из внутреннего интеграла, чтобы она не мешалась под ногами.
Ответ:
После того, как занавес опущен, повторим геометрический смысл полученного результата. По условию , следовательно, , то есть поверхность, которую задаёт эта функция двух переменных, в 1-й и 4-й четвертях расположена над плоскостью . Полученный в задаче результат – это в точности объём цилиндрического бруса, который ограничен плоскостью снизу, поверхностью – сверху и множеством перпендикулярных плоскости прямых, проходящих через каждую точку границы области («четвертинки» кольца) – сбоку. Примерно 66 «кубиков»: С задачей нахождения объёма тела мы вплотную столкнёмся при изучении тройных интегралов.
Завершим занятие несложным примером для самостоятельного решения:
Вычислить двойной интеграл, используя полярные координаты
Примерный образец чистового оформления задания в подвале.
Иногда область интегрирования приходится разбивать на две части и находить сумму двух двойных интегралов в полярных координатах, желающие могут потренироваться на Примерах № 8, 9 урока Площадь в полярных координатах. Кроме того, много дополнительных задач по теме можно раздобыть на странице готовых решений по высшей математике.
Решения и ответы:
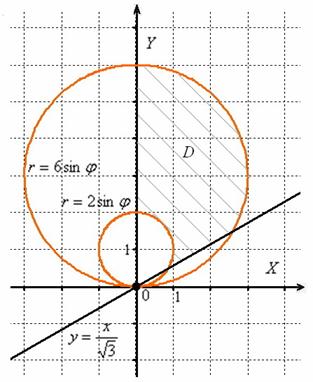
Пример 3: Решение: выделим полные квадраты и определим вид линий:
– окружность единичного радиуса с центром в точке ;
– окружность единичного радиуса с центром в точке .
Изобразим область интегрирования на чертеже:
Площадь фигуры вычислим с помощью двойного интеграла, используя полярную систему координат:
Найдём угол наклона прямой :
Порядок обхода области:
Таким образом:
1)
2)
Ответ:
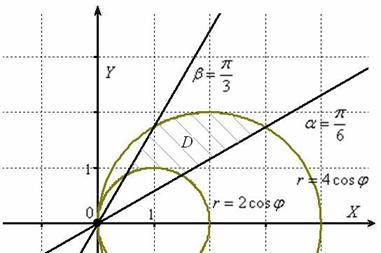
Пример 4: Решение: найдём уравнения линий в полярной системе координат:
Изобразим область интегрирования на чертеже:
Порядок обхода области:
Таким образом:
1)
2)
Ответ:

Пример 7: Решение: перейдём к полярной системе координат:
Изобразим область интегрирования на чертеже:
Порядок обхода области:
Таким образом:
1)
2)
Автор: Емелин Александр
(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам
Читайте также:


