Первообразная функции sin x равна
Таблица интегралов
Ключевые слова:первообразная функция, неопределенный интеграл, формулы интегрирования
Если F(x) - первообразная для f(x) на промежутке X, то множество всех первообразных для f(x) имеет вид F(x) + C>, где C - любое действительное число.
Это множество называют неопределенным интегралом функции y = f(x) и обозначают
$$\int f(x)dx$$: $$\int f(x)dx = F(x) + C$$
Этот математический калькулятор онлайн поможет вам вычислить неопределенный интеграл (первообразную). Программа для вычисления неопределенного интеграла (первообразной) не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс интегрирования функции.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> --> Введите подинтегральную функцию Вычислить
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу. Т.к. желающих решить задачу очень много, ваш запрос поставлен в очередь.
Через несколько секунд решение появится ниже.
Пожалуйста подождите сек.
Первообразная (неопределенный интеграл)
Ранее мы по заданной функции, руководствуясь различными формулами и правилами, находили ее производную. Производная имеет многочисленные применения: это скорость движения (или, обобщая, скорость протекания любого процесса); угловой коэффициент касательной к графику функции; с помощью производной можно исследовать функцию на монотонность и экстремумы; она помогает решать задачи на оптимизацию.
Но наряду с задачей о нахождении скорости по известному закону движения встречается и обратная задача — задача о восстановлении закона движения по известной скорости. Рассмотрим одну из таких задач.
Пример 1. По прямой движется материальная точка, скорость ее движения в момент времени t задается формулой v=gt. Найти закон движения.
Решение. Пусть s = s(t) — искомый закон движения. Известно, что s'(t) = v(t). Значит, для решения задачи нужно подобрать функцию s = s(t), производная которой равна gt. Нетрудно догадаться, что \( s(t) = \frac \). В самом деле
\( s'(t) = \left( \frac \right)' = \frac(t^2)' = \frac \cdot 2t = gt \)
Ответ: \( s(t) = \frac \)
Сразу заметим, что пример решен верно, но неполно. Мы получили \( s(t) = \frac \). На самом деле задача имеет бесконечно много решений: любая функция вида \( s(t) = \frac + C \), где C — произвольная константа, может служить законом движения, поскольку \( \left( \frac +C \right)' = gt \)
Чтобы задача стала более определенной, нам надо было зафиксировать исходную ситуацию: указать координату движущейся точки в какой-либо момент времени, например при t = 0. Если, скажем, s(0) = s0, то из равенства s(t) = (gt 2 )/2 + C получаем: s(0) = 0 + С, т. е. C = s0. Теперь закон движения определен однозначно: s(t) = (gt 2 )/2 + s0.
В математике взаимно обратным операциям присваивают разные названия, придумывают специальные обозначения, например: возведение в квадрат (х 2 ) и извлечение квадратного корня ( \( \sqrt \) ), синус (sin x) и арксинус (arcsin x) и т. д. Процесс нахождения производной по заданной функции называют дифференцированием, а обратную операцию, т. е. процесс нахождения функции по заданной производной, — интегрированием.
Сам термин «производная» можно обосновать «по-житейски»: функция у = f(x) «производит на свет» новую функцию у' = f'(x). Функция у = f(x) выступает как бы в качестве «родителя», но математики, естественно, не называют ее «родителем» или «производителем», они говорят, что это, по отношению к функции у' = f'(x), первичный образ, или первообразная.
Определение. Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке X, если для \( x \in X \) выполняется равенство F'(x) = f(x)
На практике промежуток X обычно не указывают, но подразумевают (в качестве естественной области определения функции).
Приведем примеры.
1) Функция у = х 2 является первообразной для функции у = 2х, поскольку для любого х справедливо равенство (x 2 )' = 2х
2) Функция у = х 3 является первообразной для функции у = 3х 2 , поскольку для любого х справедливо равенство (x 3 )' = 3х 2
3) Функция у = sin(x) является первообразной для функции y = cos(x), поскольку для любого x справедливо равенство (sin(x))' = cos(x)
При нахождении первообразных, как и производных, используются не только формулы, но и некоторые правила. Они непосредственно связаны с соответствующими правилами вычисления производных.
Мы знаем, что производная суммы равна сумме производных. Это правило порождает соответствующее правило нахождения первообразных.
Правило 1. Первообразная суммы равна сумме первообразных.
Мы знаем, что постоянный множитель можно вынести за знак производной. Это правило порождает соответствующее правило нахождения первообразных.
Правило 2. Если F(x) — первообразная для f(x), то kF(x) — первообразная для kf(x).
Теорема 1. Если y = F(x) — первообразная для функции y = f(x), то первообразной для функции у = f(kx + m) служит функция \( y=\fracF(kx+m) \)
Теорема 2. Если y = F(x) — первообразная для функции y = f(x) на промежутке X, то у функции у = f(x) бесконечно много первообразных, и все они имеют вид y = F(x) + C.
Методы интегрирования
Метод замены переменной (метод подстановки)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл \( \textstyle \int F(x)dx \). Сделаем подстановку \( x= \varphi(t) \) где \( \varphi(t) \) — функция, имеющая непрерывную производную.
Тогда \( dx = \varphi ' (t) \cdot dt \) и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
\( \int F(x) dx = \int F(\varphi(t)) \cdot \varphi ' (t) dt \)
Интегрирование выражений вида \( \textstyle \int \sin^n x \cos^m x dx \)
Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.
Если n и m чётные, то удобнее сделать подстановку tg x = t.
Интегрирование по частям
Интегрирование по частям — применение следующей формулы для интегрирования:
\( \textstyle \int u \cdot dv = u \cdot v - \int v \cdot du \)
или:
\( \textstyle \int u \cdot v' \cdot dx = u \cdot v - \int v \cdot u' \cdot dx \)
Сам термин "производная можно обосновать "по-житейски": функция y = f(x) "производит на свет" новую функцию y' = f '(x). Функция y = f(x) выступает как бы в качестве "родителя", но математики, естественно, не называют ее "родителем" или "производителем", они говорят, что это, по отношению к функции y' = f '(x), первичный образ, или первообразная.
Определение. Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке X, если для x є X выполняется равенство F '(x) = f(x).
1) Функция y = x 2 является первообразной для функции y = 2x, поскольку для любого x справедливо равенство (x 2 )' = 2x.
2) Функция y = sin x является первообразной для функции y = cos x, поскольку для любого x справедливо равенство (sin x)' = cos x.

При нахождении первообразных используются не только формулы, но и некоторые правила.
Правило 1. Первообразная суммы равна сумме первообразных.
Если функции у - f(x) и у - g(х) имеют на промежутке X первообразные соответственно у - F(x) и у = G(x), то и сумма функций у = f(x) + g(x) имеет на промежутке X первообразную, причем одной из этих первообразных является функция у = F(x) + G(х).
Пример 1. Найти первообразную для функции у = 2х + cos х.
Решение: Первообразной для 2х служит х 2 ; первообразной для cos х служит sin х. Значит, первообразной для функции у = 2х + cos х будет служить функция у = х 2 + sin х (и вообще любая функция вида у = х 2 + sin х + С).
Правило 2. Если F(x) — первообразная для f(x), то kF(x) — первообразная для kf(x).
Пример 2. Найти первообразные для функции y = 5 sin x.
Решение: Первообразной для sin х служит -cos х; значит, для функции у = 5 sin х первообразной будет функция у = -5 cos х.
Теорема 1. Если у = F(x) — первообразная для функции у = f(x), то первообразной для функции у = f(kx + m) служит функция у = (1/k) F(kx + m).
Теорема 2. Если у = F(x) — первообразная для функции у = f(x) на промежутке X, то у функции у = f(x) бесконечно много первообразных, и все они имеют вид у = F(x) + С.
Существуют задачи, приводящие к понятию определенного интеграла.
В задаче 1 (о вычислении площади криволинейной трапеции) приходят к выводу, что искомая площадь криволинейной трапеции равна пределу последовательности (Sn):
в задаче 2 (о вычислении массы стержня) - физическая масса равна пределу последовательности (S n ):
в задаче 3 (о перемещении точки) - искомое перемещение равно пределу последовательности (S n ):
Подробное изучение данных задач рассматривается на сайте.
Дадим математическое описание той модели, которая была построена в трех рассмотренных задачах для функции у = f(x), непрерывной (но необязательно неотрицательной, как это предполагалось в рассмотренных задачах) на отрезке [а; b]:
1) разбиваем отрезок [а; b] на п равных частей;
2) составляем сумму
Sn = f(x0) ∆ x0 + f(x 1 ) ∆ x 1 + f(x 2 ) ∆ x 2 + . + f(x k ) ∆ x k + . + f(x n-1 ) ∆ x n-1 ;
В курсе математического анализа доказано, что этот предел в случае непрерывной (или кусочно-непрерывной) функции существует. Его называют определенным интегралом от функции у = f(x) по отрезку [а; b] и обозначают так:
(читают: интеграл от а до бэ эф от икс дэ икс). Числа а и b называют пределами интегрирования (соответственно нижним и верхним).
Теорема. Если функция у = f(x) непрерывна на отрезке [а; b], то справедлива формула
где F(x) — первообразная для f(x).
Приведенную формулу обычно называют формулой Ньютона — Лейбница в честь английского физика Исаака Ньютона (1643—1727) и немецкого философа Готфрида Лейбница (1646— 1716), получивших ее независимо друг от друга и практически одновременно.
С помощью интеграла можно вычислять площади не только криволинейных трапеций, но и плоских фигур более сложного вида.
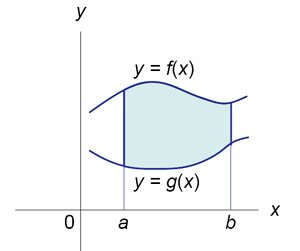
Площадь S фигуры, ограниченной прямыми х = а, х = b и графиками функций у = f(x), у = g(x), непрерывных на отрезке [а; b] и таких, что для любого х из отрезка [а; b] выполняется неравенство g(x) ≤ f(x) , вычисляется по формуле:



2. Приложение производной
Уравнение касательной к графику функции y=f(x) в точке (x0;f(x0)):
y=f(x0)+f '(x0)(x-x0); f '(x0) – угловой коэффициент касательной (тангенс угла наклона касательной).
- если f '(x)>0 в каждой точке интервала (a, b), то функция f(x) возрастает на этом интервале.
- если f '(x)<0 в каждой точке интервала (a, b), то функция f(x) убывает на этом интервале.
Необходимое условие экстремума: если x0 – точка экстремума функции f(x) и производная f ’ существует в этой точке, то f '(x0)=0.
Критические точки функции – внутренние точки области определения функции, в которых ее производная равна нулю или не существует.
- если производная при переходе через точку x0 меняет свой знак с плюса на минус, то x0 – точка максимума.
- если производная при переходе через точку x0 меняет свой знак с минуса на плюс, то x0 – точка минимума.
3. Первообразная функции

Если F(x) – первообразная для f(x) на промежутке (a, b), то любая первообразная может быть записана в виде F(x)+C, где C – некоторое действительное число.
Для вычисления первообразной рекомендуем пользоваться приведенной выше таблицей производных и приведенными ниже правилами.






Пример 3. Чему равен тангенс угла наклона касательной к графику функции у = х 2 + 2, в точке хо = – 1.
Тангенс угла наклона касательной к графику функции есть значение производной данной функции в точке хо.






На основании достаточного признака возрастания (убывания) функции имеем:


Пример 6. Найти наибольшее и наименьшее значения функции y=e x+2 -ex на промежутке [-2; 0].
1) найдём критические точки, принадлежащие отрезку [-2; 0]:

2) найдём значения функции в критической точке и на концах данного отрезка:

3) выберем наибольшее и наименьшее из полученных значений:
Пример 7. Записать уравнение касательной к графику функции f(x)=x 3 , параллельной прямой y=3x+1,5.
Уравнение касательной к графику функции y=f(x) в точке х0 имеет вид:

Так как касательная параллельна прямой y=3x+1,5, то f '(x0)=3 .





Первообразная данной функции будет F(x)=-3ctgx-7cox-2sinx+C.
Так как график первообразной проходит через точку , то координаты этой точки являются корнями уравнения. Получаем: .Задания для самостоятельного решения
Базовый уровень

8) Найдите производную функции у = х 2 (3х 5 – 2) в точке х0 = – 1.







18) Найдите максимум и минимум функции y=5x 4 -10x 2 +9.

21) Найдите наибольшее значение выражения 3х 5 – 5х 3 + 6 на отрезке [–2;2].
22) Написать уравнение касательной к параболе у = х 2 – 6х + 5 в точке пересечения её с осью ординат.


25) Исследуйте на максимум и минимум функцию у = 3х 4 – 3х 2 + 2.

27) Составьте уравнение касательной к графику функции у = х – 3х 2 в точке с абсциссой х0 = 2.










Повышенный уровень
42) Найдите значение , если .





51) Найдите наименьшее целое значение функции у = 4 х – 5∙2 х + 3,25.

53) На кривой у = 4х 2 – 6х + 3 найдите точку, в которой касательная параллельна прямой у = 2х + 3.




Ответы
1) 2е х + 6х; 2) sinx+x•cosx ; 3) – 6х + 5; 4) 18х + sinx; 5) e x -7x 6 ; 6) ; 7) 4; 8) 25; 9) – 2; 10) – 10; 11) 8; 12) – 8; 13) 6; 14) 2; 15) 0; 16) 4; 17) убывает ; возрастает ; 18) min f(-1)=f(1)=4, max f(0)=9; 19) min y(-1)=-7, max y(5)=101; 20) – 4; 21) 62; 22) у = 5 – 6х; 23) max f(1)=10; 24) max f(0)=0; min f(2)=3; 25) max f(0)=2, ; 26) 1; 27) y = – 11x + 12; 28) ; 29) 3tgx+C; 30) 7cox+C; 31) -4ctgx+C; 32) 1,2sinx+C; 33) -7sinx+C; 34) -cosx-sinx+C; 35) -2cosx-tgx+C; 36) 2tgx+ctgx+C; 37) ; 38) ; 39) 1; 40) ; 41) ; 42) – 0,5; 43) 1; 44) 0; 45) – 2; 46) 4; 47) – 1; 48) ; 49) при а = 1; 50) – 1, 3; 51) – 3; 52) ; 53) (1; 1); 54) – 1; 55) 1; 56) ; 57) 3; 58) ; 59) 3; 60) 5.Словами это читается так: интеграл от синуса равен сумме отрицательного косинуса и произвольной постоянной.
Напрямую интеграл взять не получится, так как аргумент синуса и знака дифференциала отличаются. Выполняем подведение под дифференциал $ 2x $ и добавляем перед интегралом дробь $ \frac $:
$$ \int \sin 2x dx = \frac \int \sin 2x d(2x) = -\frac \cos 2x + C $$
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
В данном случае необходимо воспользоваться одной из тригонометрических формул. Конкретно формулой понижения степени синуса: $$ \sin^2 x = \frac $$
Заменяем выражение под интегралом:
$$ \int \sin^2 x dx = \int \frac dx = \frac \int (1-\cos 2x) dx = $$
$$ = \frac \int 1dx - \frac \int \cos 2x dx = \fracx - \frac\cdot\frac\int \cos 2x d(2x) = $$
Здесь нужно вспомнить свойство степеней и учесть: $$ \sin^3 x = \sin x \cdot \sin^2 x $$
Подставляем, полученное выражение в интеграл и заносим $ \sin x $ под знак дифференциала:
$$ \int \sin^3 x dx = \int \sin x \sin^2 x dx = - \int \sin^2 x d(\cos x) = $$
Далее используем свойство $ \sin^2 x = 1 - \cos^2 x $:
$$ = -\int (1-\cos^2 x) d(\cos x) = -\int d(\cos x) + \int \cos^2 x d(\cos x) = $$
$$ = - \cos x + \frac + C = \frac \cos^3 x - \cos x + C $$
$$ \int \sin^3 x dx = \frac \cos^3 x - \cos x + C $$
Вычисление начнем как в случае с неопределенным интегралом и в конце используем формулу Ньютона-Лейбница $ \int_a^b f(x) dx = F(x) \bigg |_a^b = F(b)-F(a) $:
$$ \int_0^\pi \sin x dx = -\cos x \bigg |_0^\pi = -\cos \pi + \cos 0 = -(-1) + 1 = 1+1=2 $$
Читайте также:


