Найти наименьший положительный период функции y sin x 7

Что бы найти наименьший положительный период , нужно знать период
обычной тригонометрической функции (в нашем случае , известно что ее период ) и действовать по следующей формуле:
- где Т это период обычной тригонометрической функции, а К это число стоящее перед иксом.
Это и есть искомый период.
Если что то не понятно, пишите в комментарии, с радостью отвечу.
Онлайн калькулятор для определения периодичности функции. Периодическая функция - это функция повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (периода функции) на всей области определения.
Периодичная функция может иметь и несколько периодов, самый маленький положительный из них называется основным.

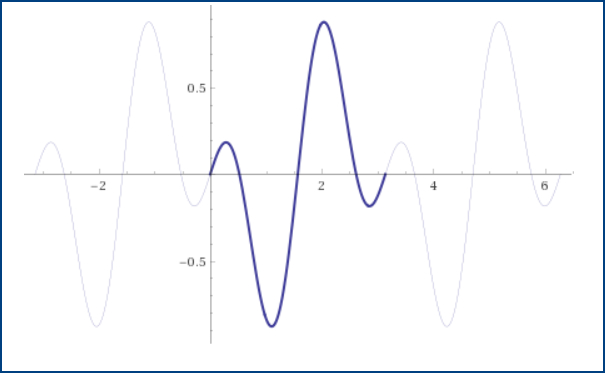
Типичная школьная задача - нахождение периода функции. Теперь вы можете решить эту быстро онлайн с помощью нашего калькулятора. Для это надо только ввести команду «period» и функцию для которой надо найти период. Кроме того что будет выведен период, если он есть, будет еще и график построен (как на рисунке слева) на котором будет показана величина периода. Чтобы воспользоваться онлайн сервисом нажмите значок копирования, чтобы добавить команду из примера в окно ввода команд для обработки изображений.

На этом уроке мы рассмотрим периодичность функций у = sin t и у = cos t. В начале урока мы обсудим, откуда возникает периодичность у тригонометрических функций, вспомним, что такое координатная прямая и числовая окружность и как отображаются тригонометрические функции на числовой окружности. Далее дадим определение периодической функции и периода и найдем наименьший положительный период для функций синуса и косинуса. Также рассмотрим, как период влияет на исследование функции, рассмотрим графики функции синуса и косинуса на наименьшем положительном периоде и решим ряд задач с использованием периодичности этих функций.
Если у вас возникнет сложность в понимании тему, рекомендуем посмотреть урок «Тригонометрия»
Читайте также:


