Функция у sin x ее свойства и график видеоурок

На этом уроке мы продолжим изучение тригонометрической функции у = sin х и решим типовые задачи. Вначале рассмотрим основные точки этой функции на промежутке [-π/2;π/2] на графике и на круге и выясним основные особенности функции на этом промежутке. Решим несколько примеров на чтение графика и сформулируем типовую прямую и обратную задачу для этой функции на рассматриваемом промежутке. Подробно рассмотрим монотонность функции на заданном промежутке и решим задачи с ее использованием. Далее рассмотрим модификации графика функции, а именно: сдвиг кривой вправо и влево, а также вверх и вниз. Решим несколько примеров на построение графика.
Если у вас возникнет сложность в понимании тему, рекомендуем посмотреть урок «Тригонометрия»

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности



Конспект урока "Функция у = sin x и её график"
Сегодня на уроке мы с вами поговорим о функции . Познакомимся с графиком функции . А также рассмотрим основные свойства этой функции.
Прежде чем приступить к рассмотрению новой темы, давайте напомним, что функция определена на всей числовой прямой, а множеством её значений является отрезок . Значит, эта функция ограничена и её график расположен в полосе между прямыми и . Также мы знаем, что функция является нечётной и периодической с периодом . Её график можно построить таким же образом, как мы строили график функции , также начиная построение, например, на отрезке , а затем распространив график по всей числовой прямой с помощью сдвигов. Но давайте с вами поступим следующим образом.

Вспомним формулу приведения .
, , .
Известно, что график функции , где , получается из графика функции сдвигом вдоль оси абсцисс на единиц вправо.
Таким образом, мы получили формулу, которая показывает, что график функции можно получить сдвигом графика функции вдоль оси абсцисс вправо на .


Кривая, являющаяся графиком функции , называется синусоидой.

График функции хорошо иллюстрирует её свойства. Давайте поговорим об основных свойствах функции.

Итак, мы уже знаем, что область определения функции – множество всех действительных чисел, а множество значений – отрезок .

Функция нечётная. Её график симметричен относительно начала координат. Данная функция периодическая с периодом .
Функция принимает значение, равное , при , .
Функция принимает наибольшее значение при , , а наименьшее значение при , .
при , .
при , .
Возрастает функция на отрезках , .
Убывает функция на отрезках , .
А сейчас давайте выполним несколько заданий.
Задание первое. Найдите все корни уравнения , принадлежащие отрезку .

Задание второе. Найдите все решения неравенства , принадлежащие отрезку .

Задание третье. Выразив косинус через синус по формулам приведения, сравните числа:

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности



Конспект урока "Функция y=sinx, ее свойства и график"
· познакомиться с функцией y = sin (x);
· познакомиться с основными свойствами функции y = sin (x);
· познакомиться с графиком функции y = sin (x).
Давайте вспомним, как мы вводили тригонометрическую функцию числового аргумента sin t.

Давайте вспомним, что же значит – исследовать функцию.

На сегодняшнем уроке мы с вами исследуем функцию y = sin (x) и, по результатам исследования, построим её график.
Область определения

Область значения

Исследование функции на монотонность

Исследование функции на ограниченность

Наибольшее и наименьшее значения функции

Прежде чем исследовать функцию на чётность, давайте вспомним алгоритм исследования функции на чётность.

Исследование функции на четность

Давайте ещё раз повторим свойства функции y = sin (x).

Построим график функции y = sin (x). Для удобства построения, в качестве масштаба по оси Oy возьмём две клеточки, в качестве масштаба по оси Ox возьмём три клеточки.

Линию, служащую графиком функции y = sin (x), называют синусоидой.
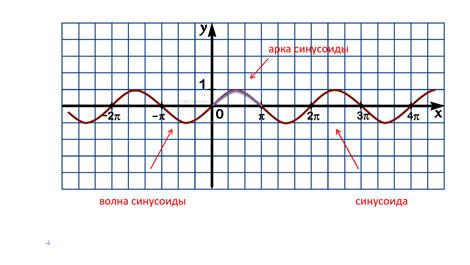
Опираясь на построенный график, отметим ещё одно свойство функции y = sin (x).

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности



Конспект урока "Функция y=sinx, ее свойства и график"
· познакомиться с функцией y = sin (x);
· познакомиться с основными свойствами функции y = sin (x);
· познакомиться с графиком функции y = sin (x).
Давайте вспомним, как мы вводили тригонометрическую функцию числового аргумента sin t.

Давайте вспомним, что же значит – исследовать функцию.

На сегодняшнем уроке мы с вами исследуем функцию y = sin (x) и, по результатам исследования, построим её график.
Область определения

Область значения

Исследование функции на монотонность

Исследование функции на ограниченность

Наибольшее и наименьшее значения функции

Прежде чем исследовать функцию на чётность, давайте вспомним алгоритм исследования функции на чётность.

Исследование функции на четность

Давайте ещё раз повторим свойства функции y = sin (x).

Построим график функции y = sin (x). Для удобства построения, в качестве масштаба по оси Oy возьмём две клеточки, в качестве масштаба по оси Ox возьмём три клеточки.

Линию, служащую графиком функции y = sin (x), называют синусоидой.

Опираясь на построенный график, отметим ещё одно свойство функции y = sin (x).
Читайте также:


