Функция cos и sin в с
Величины углов (аргументы функций): \( \alpha \)
Тригонометрические функции: \( \sin \alpha \) , \( \cos \alpha \) , \( \tan \alpha \) , \( \cot \alpha \) , \( \sec \alpha \) , \( \csc \alpha \)
Целые числа: \( n \)
Периодической называется функция, которая повторяет свои значения через какой-то регулярный интервал, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода функции): существует такое ненулевое число \(T\) (период), что на всей области определения функции выполняется равенство \( f(x)=f(x+T) \) .
Тригонометрические функции (синус, косинус, тангенс, котангенс) являются периодическими.
\( \sin(x+2k\pi)=\sin x,\;\cos(x+2k\pi)=\cos x,\;k\in\mathbb. \)
Тригонометрические функции \( \sin \alpha \) и \( \cos \alpha \) являются периодическими, с наименьшим периодом равным \( 2 \pi \) .
Тригонометрические функции \( \tan \alpha \) и \( \cot \alpha \) являются периодическими, с наименьшим периодом равным \( \pi \) .
Здравствуйте.
Начал писать игру, аналог знаменитых Tank Wars.
При использовании библиотечных(math.h) функций sin и cos появилась проблема.
Обе функции возвращают значение в радианах. И вот выходит несостыковка.
sin 30 == 0.5
функция sin(30) возвращет
(-0.988) радиан
Как известно для перевода радиан в градусы их нужно умножить на 180 и разделить на ПИ.
-0,988*180/3,14 получаем
Синусы, косинусы нужны обязательно в градусах, для формул перемещения тела.
Объясните ошибку и вариант её избежания, возможно функцию, возвращающую значения в градусах.
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Построить массив по правилу: X[i]=(cos 1 +. + cos i) / (sin 1 +. + sin i)
Помогите, построить одномерный вещественный массив X из n элементов (n - константа).Я знаю, что.
Из Sin в Cos С++
Здраствуйте, мне нужно написать програму которая за рядами Тейлора выводит косинус . Проблема.
Sin() cos()
Всем приветик. У меня последний Qt MinGW. Вопрос: Перед использованием функции sin(x), мне.
Постановка задачи. Вычислить значение тригонометрической функции sin(x) от произвольного значения аргумента x.
Вариант решения 1. Поищем готовый вариант решения. Тригонометрия – раздел математики. Предположим, что в библиотеке System реализован класс, связанный с математическими функциями (в библиотеках прежних языков всегда была функция извлечения квадратного корня из числа – sqrt()). Как же узнать название класса?
Воспользуемся интеллектуальной подсказкой. Внутри метода Main() консольного приложения наберем одну букву M в английской раскладке. В выпадающем меню выберем класс Math (по-английски математика – Mathematics или maths). Наведя мышкой на это слово, прочитаем:
«class System.Math. Предоставляет константы и статические методы для тригонометрических, логарифмических и иных общих математических функций».
Мы почти у цели.
Программа, реализующая вычисление sin(a), угол а задан в градусах, представлена ниже:
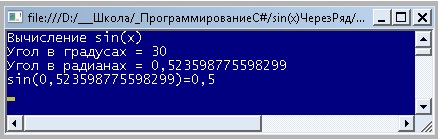
Результат выполнения программы:
Вариант решения 2.

Заглянем в справочник по высшей математике, раздел «Ряды». Из него мы узнаем, что функция sin(x) может быть представлена бесконечным рядом:
В теории, вы скажете все красиво, но бесконечный ряд – это бесконечное время вычислений, кроме того, возможно переполнение при возведении в степень и вычислении знаменателя.
То есть каждый следующий член ряда будет вносить в сумму все меньший и меньший вклад, поэтому можно использовать столько членов ряда, сколько нужно для достижения заданной точности вычислений. Например, если n=9, то | r11 / r9 | <=1/110 (более чем в 100 раз).
Что следует предпринять, если |x| >> 1 (много больше 1), ведь в этом случае наш критерий работать не будет? Тут пригодится знание такого свойства функции sin(x) как периодичность. Для угла x, заданного в радианах:
sin(x+2πk) = sin(x), где k – любое целое число, 0, ±1, ±2, ±3, … .
Для угла а, заданного в градусах:
sin(a+360°·k) = sin(a), где k – любое целое число.
Таким образом, если угол х по модулю не будет больше 2π, |x|<=2π, то тогда оценка отношения двух соседних членов ряда не превысит:
|rn+2 / rn | = 4π 2 / ((n+2)(n+1))
т.е., начиная с n=7 убывание гарантировано.
Наша функция, также как и библиотечная, получает на вход значение угла в радианах и возвращает значение sin(x). Тип аргумента и самой функции задан как double. Приступим к разработке начинки метода Sin2() – блока в фигурных скобках.
Короткая версия: я хотел бы знать, существуют ли реализации стандартных тригонометрических функций, которые быстрее, чем те, которые включены в math.h .
Длинная версия: у меня есть программа, которая довольно тяжелая на цифрах (это физическая симуляция) и которая должна вызывать тригонометрические функции, в основном sin и cos , много. В настоящее время я просто использую реализации, включенные в math.h . Профилирование показывает, что вызовы этих функций стоят больше, чем я ожидал (надеявшийся).
Хотя в других частях кода, безусловно, есть много места для оптимизации, более быстрые sin и cos могут дать мне некоторые дополнительные проценты.. Итак, у вас есть какие-нибудь предложения?
В другом посте предлагается использовать самодельные таблицы подстановки. Но, может быть, есть альтернативы? Или готовые и хорошо протестированные решения поиска в некоторых библиотеках?
Если вы хотите использовать пользовательскую реализацию, смотрите здесь, здесь и здесь
Также здесь (Перейдите к универсальной SIMD-Mathlibrary), если вам нужно вычислить sin/cos для больших массивов
Можно также попробовать использовать встроенные компоненты SSE C++. Смотрите здесь
Обратите внимание, что большинство современных компиляторов поддерживают оптимизацию SSE и SSE2. Например, для Visual Studio 2010 его необходимо включить вручную. Как только вы сделаете это, другой реализация будет использоваться для большинства стандартных математических функций.Еще один вариант - использовать DirectX HLSL. Посмотрите сюда . Обратите внимание, что есть хорошие функции sincos, которые возвращают как sin, так и cos.
Обычно я использую IPP (который не является бесплатным). Подробнее смотрите здесь
А) попытка сэкономить небольшие проценты не принесет большого удовлетворения. Финиш в 97 вместо 100 часов-это еще долго.
B) вы говорите, что профилировали, и что тригонометрические функции занимают больше времени, чем вам хотелось бы. И сколько же? а как насчет всего остального времени? Вполне возможно, что у вас есть более крупная рыба для жарки. Большинство профилировщиков , основанных на концепциях gprof, не сообщают вам о вызовах среднего стека, на которых вы могли бы сосредоточиться, чтобы сэкономить больше времени. Вот пример: образец.
Давным-давно на медленных машинах люди использовали массивы с заранее вычисленными значениями. другой вариант для вычисления с вашей собственной точностью, как это: (ищите "определения рядов")
Вы можете посмотреть на это. Это говорит об оптимизации греха, cos.
Для 2-3% выигрыша это почти наверняка не стоит риска неточности, ошибки, предположений, которые больше не являются истинными (например, никогда не выходят за пределы [-1,-1] ) и т. д., если только вы не планируете запустить это на огромном количестве машин (где 2-3% представляют тысячи или миллионы долларов в электроэнергии и амортизированной стоимости машины).
Тем не менее, если у вас есть знание предметной области о том, чего вы пытаетесь достичь, вы можете ускорить свои вычисления на коэффициент два или больше. Например, если вам всегда нужны sin и cos одного и того же значения, вычислите их близко друг к другу в коде и убедитесь, что ваш компилятор переводит их в инструкцию сборки FSINCOS (см. этот вопрос). Если вам нужна только небольшая часть полного диапазона функции, вы можете потенциально использовать набор полиномов низкого порядка с последующей итерацией метода Ньютона для получения полной точности машины (или столько, сколько вам нужно). Опять же, это очень много более мощный, если вы знаете, что вам нужны только некоторые значения-например, если вы можете использовать, что sin(x) близок к x около нуля, и вам будут нужны только значения около нуля, тогда вы можете резко уменьшить количество нужных вам терминов.
Но, опять же, мой главный совет: 2-3% не стоит того. Подумайте лучше об используемых алгоритмах и других потенциальных узких местах (например, не ест ли Мэллок слишком много времени?) прежде чем вы оптимизируете это.
Всё зависит от требуемой точности: чем она меньше, тем функция будет быстрее. Для вычислений с одинарной точностью, как правило, требуется многочлен Чебышёва с 5-ю слагаемыми. Такая функция будет работать быстрее, чем любая стандартная реализация, и даже, может быть, быстрее, чем реализация с помощью таблицы и интерполяции. Для вычислений с двойной точностью наилучшая производительность достигается методом Паде-Чебышёва. Скорее всего, она тоже будет превосходить производительность стандартных библиотечных функций, особенно если использовать в коде инструкции из набора FMA. Но для построения подобных аппроксимаций требуются определённые навыки.
В качестве примера приведу код для функции тангенс аргумента, заданного в градусах. Используются одинарная точность и SSE-инструкции. Здесь b0, . b4 - коэффициенты степенного ряда, полученного путём приведения подобных в частичной сумме ряда Чебышёва для функции f(t)=t/tg(pi*t/4), |t|<=1.
_declspec(naked) float _vectorcall tand(float x) // Тангенс в градусах
static const float ct[6] = // Таблица констант
-0.0111111111f, // -1/90 - множитель для приведения x
57.2957793f, // b0*45
-5.81775793E-3f, // b1/45
-1.18170581E-7f, // b2/45^3
-3.39436425E-12f, // b3/45^5
-1.22505855E-16f // b4/45^7
>;
_asm
mov edx, offset ct // В edx - адрес таблицы констант
movss xmm1, [edx] // xmm1 = -1/90
mulss xmm1, xmm0 // xmm1 = -x/90
cvtss2si ecx, xmm1 // ecx = -k, где k - округлённое до целых значение x/90
imul ecx, 90 // ecx = -90*k
jno tg_cont // В случае слишком большого |x| считать, как при x=0
sub ecx, ecx // Для этого обнуляем ecx,
xorps xmm0, xmm0 // и обнуляем xmm0
tg_cont: // Продолжаем для корректного значения x
cvtsi2ss xmm2, ecx // xmm2 = -90*k
shl ecx, 30 // При нечётном k установить знаковый бит ecx
addss xmm2, xmm0 // xmm2 = x-90*k = 45*t - в диапазоне [-45; 45]
movd xmm1, ecx // В xmm1 - знаковая маска результата
movss xmm0, [edx+20] // xmm0 = b4/45^7 - инициализировать сумму
xorps xmm1, xmm2 // xmm1=(-1)^k*45*t - выставить правильный знак будущего результата
mulss xmm2, xmm2 // xmm2=(45*t)^2 - подготовить аргумент для вычисления многочлена
mov cl, 4 // ecx = 4 или 80000004h - инициализировать счётчик цикла
tg_loop: // Цикл вычисления многочлена по схеме Горнера
mulss xmm0, xmm2 // Умножить последний результат на аргумент многочлена
addss xmm0, [edx+ecx*4] // Прибавить текущий коэффициент
_emit 0x67 // Префикс изменения разрядности для получения команды loopw
loop tg_loop // Учесть все 5 коэффициентов. В xmm0 формируется 45*f(t)
jnz tg_div // Перейти для вычисления -f(t)/t, если k нечётное, т.е. |tg x|>1
movaps xmm2, xmm0 // Для чётного k обменять местами регистры xmm0 и xmm1
movaps xmm0, xmm1 // В этом случае |tg x|<=1, и нужно считать t/f(t)
movaps xmm1, xmm2 // Теперь xmm1 = 45*f(t), xmm0 = 45*t
tg_div: // Получение окончательного результата
divss xmm0, xmm1 // Найти -f(t)/t, если k нечётное, или t/f(t), если k чётное
ret // Вернуться
>
>
Читайте также:


