Оригами правильный пятиугольник
Как сделать пятиугольник, How to make a pentagon. Бумага цветная, односторонняя. Размер листа для цветка А4 (204 мм .
Всем Привет! С вами RAIDO TV и на нашем семейном канале вы увидите кучу крутых ПЛАСТИЛИНовых мастер-классов, .
На видео показано как построить пятиугольник циркулем и разделить окружность на 5 частей с помощью циркуля.
Построение правильного пятиугольника в программе КОМПАС-3D. Аналогичным образом можно построить правильный .
Много красивых поделок оригами можно сложить из пятиугольника, который легко сделать из квадрата бумаги любого .
1 способ - с помощью сгибаний (оригами) 2 способ - с помощью транспортира 3 способ - с помощью циркуля и линейки.
Икосаэдр − правильный многогранник с 20 гранями, имеющими форму треугольника. Выполняем чертеж развертки .
Как из листа бумаги сделать пятиугольник, смотрите в новом видео. Украсив такой пятиугольник мелкими деталями, можно .
И это НЕСКУЧНОЕ ЧЕРЧЕНИЕ. Мы продолжаем изучать геометрическое черчение. В данном коротком ролике я покажу и .
Всем Привет! С вами RAIDO TV и на нашем семейном канале вы увидите кучу крутых ПЛАСТИЛИНовых мастер-классов, .
На видео показано как построить пятиугольник с заданной стороной циркулем, то есть достроить отрезок до .
На этом 4K UHD видео показаны различные способы построения правильного пятиугольника с использованием циркуля и .

Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел .
Додекаэдр имеет следующие характеристики :
- Тип грани – правильный пятиугольник;
- Число сторон у грани – 5;
- Общее число граней – 12;
- Число рёбер, примыкающих к вершине – 3;
- Общее число вершин – 20;
- Общее число рёбер – 30.
Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324°.
Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.
Математические характеристики додекаэдра

Додекаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.
Радиус описанной сферы додекаэдра
где a - длина стороны.

Сфера может быть вписана внутрь додекаэдра.
Радиус вписанной сферы додекаэдра


Площадь поверхности додекаэдра.
Для наглядности площадь поверхности додекаэдра можно представить в виде площади развёртки.
Площадь поверхности можно определить как площадь одной из сторон додекаэдра (это площадь правильного пятиугольника) умноженной на 12. Либо воспользоваться формулой:


Объем додекаэдра определяется по следующей формуле:
Вариант развертки
Додекаэдр можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка - единая деталь с линиями сгибов.
Древнегреческий философ Платон по одной из версий не относил додекаэдр ни к одному из земных элементов, а по другой из версий ассоциировал додекаэдр с эфиром (пустотой). Для построения модели этого правильного многогранника мы выбрали желтый цвет.

Заметим, что это не единственный вариант развертки.
Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4:
- если Вы предполагаете распечатать на цветном принтере - цветная развертка
- если Вы предполагаете использовать для сборки цветной картон - развертка
Кроме того, существуют два классических варианта окраски многогранника, когда каждая из соседних граней окрашена в свой цвет. Либо используется определенное количество цветов раскраски, причем одинаковые цвета не граничат друг с другом.
Представляем Вашему вниманию два варианта окраски додекаэдра с использованием шести и четырех цветов.
Первый вариант - шесть цветов: скачать развертку
Второй вариант - четыре цвета: скачать развертку
Видео. Додекаэдр из набора "Волшебные грани"
Вы можете изготовить модель додекаэдра воспользовавшись деталями для сборки из набора "Волшебные грани".


Сборка многогранника из набора:
Подробная сборка от Алексея Жигулева (youtube-канал Оригами)
вращение готового многогранника:
Видео. Вращение всех правильных многогранников
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
- Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.
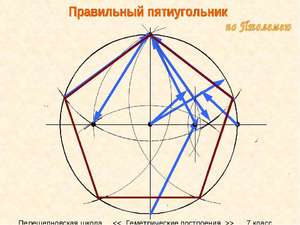
Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
Интересные факты
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.

Здравствуйте коллеги.
Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.
Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.
Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.
Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:
Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.
Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.
Как выглядит пятиугольник и звезда
Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.

Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.

Теперь от точки В до точки С проведем прямую.

Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.

И отрезок DB. Картинка внизу.

Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.

Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.

Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.

Такие же отрезки наносим на всей части круга. Смотрим картинку.

На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.

Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.
Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.
Последние события
Рисуем цыпленка
Вот такого цыпленка вы сможете нарисовать, если вы выполните все действия четко по шагам. Пробуйте и все у вас получится!
Елка-раскраска на стену

А так как скоро Новый Год, предлагаю скачать шаблон большой елки-раскраски. Этот шаблон состоит из 22 двух листов формата А4. На них нанесен и основной рисунок, и линии по которым нужно эти листочки склеить.
Дедушка Мороз и дети

Дед Мороз, Снегурочка, Снеговик, птицы и звери в лесу , дети на новогоднем празднике – вот герои этой книжки-раскраски. А создал их художник В. Жигарев.
Маша и Медведь. Зимние раскраски

Мультик про шуструю озорную маленькую девочку Машу и ее приятеля медведя нравится всем – и детишкам, и их родителям.
Раскраски с дедом Морозом

Новый год наступил. Но впереди еще старый новый год, да и зима еще вся впереди. Раскрашиваем картинки с Дедом Морозом и Снегурочкой.
Раскраски к новому году

Новогодние раскраски. Зима, елка, дед Мороз в санях, подарки. Скачайте забавные картинки, пусть они напоминают вам о веселом празднике.
Новогодняя елка. Раскраски
Символ Нового года – елочка, украшенная игрушками, гирляндами, мишурой.
Скачайте раскраски с новогодней елкой. Картинку можно не просто раскрасить, а превратить в поздравительную открытку.
Популярное
Архив

Как нарисовать правильную звездочку? Как нарисовать правильный пятиугольник? Как разделить круг на пять равных частей? На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной эти шаги.
Как нарисовать правильную звездочку?
Как нарисовать правильный пятиугольник?
Как разделить круг на пять равных частей?
На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной вот эти шаги.
Конечно же, нам понадобится циркуль с карандашом и линейка.
Для начала нарисуйте циркулем круг.
Разделите его на четыре части линиями сверху вниз и справа налево.
Можно сразу объяснить ребенку, что отрезок, соединяющий две точки на окружности и проходящий через ее центр, называется диаметр.

Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел .
Додекаэдр имеет следующие характеристики :
- Тип грани – правильный пятиугольник;
- Число сторон у грани – 5;
- Общее число граней – 12;
- Число рёбер, примыкающих к вершине – 3;
- Общее число вершин – 20;
- Общее число рёбер – 30.
Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324°.
Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.
Математические характеристики додекаэдра

Додекаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.
Радиус описанной сферы додекаэдра
где a - длина стороны.

Сфера может быть вписана внутрь додекаэдра.
Радиус вписанной сферы додекаэдра


Площадь поверхности додекаэдра.
Для наглядности площадь поверхности додекаэдра можно представить в виде площади развёртки.
Площадь поверхности можно определить как площадь одной из сторон додекаэдра (это площадь правильного пятиугольника) умноженной на 12. Либо воспользоваться формулой:


Объем додекаэдра определяется по следующей формуле:
Вариант развертки
Додекаэдр можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка - единая деталь с линиями сгибов.
Древнегреческий философ Платон по одной из версий не относил додекаэдр ни к одному из земных элементов, а по другой из версий ассоциировал додекаэдр с эфиром (пустотой). Для построения модели этого правильного многогранника мы выбрали желтый цвет.

Заметим, что это не единственный вариант развертки.
Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4:
- если Вы предполагаете распечатать на цветном принтере - цветная развертка
- если Вы предполагаете использовать для сборки цветной картон - развертка
Кроме того, существуют два классических варианта окраски многогранника, когда каждая из соседних граней окрашена в свой цвет. Либо используется определенное количество цветов раскраски, причем одинаковые цвета не граничат друг с другом.
Представляем Вашему вниманию два варианта окраски додекаэдра с использованием шести и четырех цветов.
Первый вариант - шесть цветов: скачать развертку
Второй вариант - четыре цвета: скачать развертку
Видео. Додекаэдр из набора "Волшебные грани"
Вы можете изготовить модель додекаэдра воспользовавшись деталями для сборки из набора "Волшебные грани".


Сборка многогранника из набора:
Подробная сборка от Алексея Жигулева (youtube-канал Оригами)
вращение готового многогранника:
Видео. Вращение всех правильных многогранников
Популярное
Современный кинематограф постарался привлечь внимание зрителя, используя геометрические формы "инопланетного происхождения".
Многогранники могут стать украшением вашего дома, создав изюминку в интерьере.
Сделать новогодний праздник красивым и необычным, чтобы дети видели в нём сказку, а гости восхищались, можно только своими руками. Бумажные многогранники –.
АРХИМЕД (287 - 212 до н.э.) - древнегреческий математик, физик и механик. Архимед - автор многочисленных открытий и изобретений: машины для.
Это новый, весьма необычный способ создать модель Звёздчатого многогранника открытого 1619 году немецким математиком и астрономом Иоганном Кеплером.
Знакомые каждому с детства коробочки для Биг-Мака и картошки, стаканчик для Кока-Колы так же делают из бумажных разверток.
У каждого из пяти тел Платона можно определить следующие математические характеристики: 1. Радиус сферы описанной вокруг многогранника; 2. Радиус сферы.
Читайте также:


