Кубооктаэдр оригами схема
Сделать из бумаги многогранник — Икосаэдр очень просто в технике оригами из модулей Mitsunobu Sonobe.
Такая интересная поделка кусудама станет интересным украшением или подарком, способным удивить друзей. Бумажный шар кусудама станет к тому же интересной елочной игрушкой на Новый год и отлично украсит новогоднюю елку на праздник.
Сделать икосаэдр не сложно и собирается он из 30 простых модулей, которые изготавливаются из квадратного листа бумаги, мы использовали бумагу размером 7*7 см.

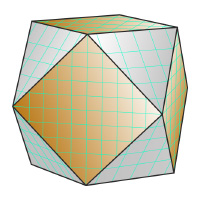
Кубооктаэдр - полуправильный выпуклый многогранник, обладающий двумя свойствами:
1. Все грани являются правильными многоугольниками двух типов - треугольник и квадрат;
2. Для любой пары вершин существует симметрия многогранника (то есть движение, переводящее многогранник в себя) переводящая одну вершину в другую.

Архимедовы тела являются полуправильными многогранниками в том смысле, что их грани - правильные многоугольники, но они не одинаковы при этом сохраняется условие одного из типов пространственной симметрии: тетраэдрического, октаэдрического или икосаэдрического.
Математические характеристики кубооктаэдра

Кубооктаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.
Радиус описанной сферы кубооктаэдра
где a - длина стороны.
Напротив, поместить сферу внутрь кубооктаэдра так, чтобы она касалась одновременно всех сторон не удастся. Для выполнения этого условия сфера должна касаться всех квадратов и треугольников. Но расстояния разные.
Площадь поверхности кубооктаэдра.
Площадь поверхности можно определить по следующей формуле:

Объем кубооктаэдра определяется по следующей формуле:

Кубооктаэдр можно разделить плоскостью на две равные части.
При этом сечение будет иметь форму правильного шестиугольника.
Возможны следующие четыре варианта разреза кубооктаэдра:




Знаменитая математическая задача "О семи кёнигсбергских мостах" или Путь Эйлера может быть переформулирована и рассмотрена на примере ребер кубооктаэдра.
Как последовательно обойти все ребра кубооктаэдра? Одного ребра нельзя касаться дважды.
На рисунке приведен анимационный пример решения этой задачи.
Одно из названий задачи - Путь Эйлера. В честь знаменитого математика Леонарда Эйлера.
Интересная оригами модель многогранника - Кубооктаэдр. Сделать такую модель очень просто, используя бумагу размером 8*8 см. или иной другой размер в зависимости от ваших предпочтений.
Скопируйте код и вставьте в окошко создания записи на LiveInternet, предварительно включив там режим "Источник"
| Интересная оригами модель многогранника - Кубооктаэдр. Сделать такую модель очень просто, используя бумагу размером 8*8 см. или иной другой размер в зависимости от ваших предпочтений. Читать полностью |
Построим каркасный дом вашей мечты
Каркасный дом с мансардой V197 "Демополис"
Каркасный дом с мансардой, 3 спальнями и террасой V062 "Бартлесвиль"
Каркасный дом с мансардой V204 "Андалусиа"
Каркасный дом с 2 спальнями V028 "Ньюкасл"
Комментарии
Вставка изображения
Можете загрузить в текст картинку со своего компьютера:
. или указать адрес картинки в интернете:
Загрузка списка альбомов.
Вставка изображения

Чаще всего на сайте читают:
Сегодня пришлось мне поутру отводить сына на уроки. Проводила до дверей, дала ЦУ, поворачиваюсь обратно ехать. И тут бабушка его одноклассницы мне в спину говорит: "Вяжет-вяжет, а у самой дети брошенные! Детьми надо заниматься!" Вот почему так, ведь рукодельничаю я в ущерб своему свободному времени, сну в основном, а не в то время, когда с детишками.
В передаче "Тайны Мира" сейчас говорили про волшебные свойства соды. Без всяких диет и упражнений полежала в ванной 20 минут и все, пара кило ушли.
В марте месяце были съемки с моим участием в программе "Модный приговор". Ничего хорошего об этой передаче вспомнить я не могу, хотя было немало приятных моментов. Но самое страшное - мне обрезали волосы. И вот сижу я сейчас, смотрю на себя в зеркало и понимаю что только об этом и помню.
У моего 16-летнего брата завелась девушка. И вот я совершенно случайно подслушала их разговор. Собрался братишка к пассии своей в гости и мой муж дает ему наставления. Муж - "Как придешь к ней домой сразу просись в туалет, не стесняйся. А там загляни под крышку унитаза. Если обнаружишь сам знаешь что, то смело сваливай от неряхи и стирай ее номер телефона".
Создание моделей правильных многогранников с помощью разверток
Чаще всего при создании моделей многогранников из плоских разверток используют такие развертки, в которых грани прилегают друг к другу ребрами, а модель строится путем загибания развертки вдоль ребер. Например, при создании моделей правильных многогранников чаще всего используют следующие развертки

Но хотелось бы показать и другие развертки, которые удовлетворяют всем условиям определения развертки многогранника, а также условиям теоремы Александрова, но их стороны не являются ребрами многогранника.

Например, в данной развертке, состоящей из единственного многоугольника, ни одна из сторон не является ребром куба, который получается из этой развертки.

В недалеком прошлом молоко разливали в пакеты, которые имели форму не параллелепипеда как сейчас, а тетраэдра. Такую тару было легко изготавливать. Сначала прямоугольная лента склеивается в цилиндр, горизонтальные края которого затем заклеиваются в двух взаимно перпендикулярных плоскостях. Развертка такого тетраэдра - прямоугольник, стороны которого разбиваются на меньшие отрезки-ребра, попарное отождествление которых показано на рисунке. Данная развертка удовлетворяет обоим условиям теоремы Александрова.
Создание моделей правильных многогранников методами оригами
Сегодня оригами переживает очередную волну интереса. Появились новые направления оригами и области его применения. Так, математики открыли множество возможностей для решения геометрических и топологических задач. Архитекторы и строители увидели в оригамном конструировании возможности для создания многогранных структур из плоского листа. Даже возник новый термин - "оригамика". Для педагогов оригами уникальная возможность развития тонкой моторики ребенка, что прямо связано с развитием интеллекта. Для психологов оригами - это одно из направлений арттерапии, возможности оказания психологической помощи больному посредством искусства.
Остановимся более подробно на создании моделей правильных многогранников методами оригами. Существует несколько методов для создания одного и того же многогранника. Мной были изучены и опробованы при создании моделей правильных многогранников 4 метода оригами.











Создание моделей правильных многогранников с помощью модуля Шеремет Г.Г
Создание моделей правильных многогранников из квадратного листа бумаги



Данные модели наименее трудоемкие и одни из самых простых в сборке, схема их сборки приводится в Приложении 4
Создание моделей правильных многогранников с помощью модуля Miyuki Kawamura


При использовании модулей Miyuki Kawamura модели получаются, составленными из ребер. Это удобно, если необходимо представить, как будет выглядеть диагональ многогранника или его сечение. Книга [4] этого автора пока еще не переведена на русский язык, мне пришлось изучать ее на английском языке, но, несмотря на это материал мне был понятен и интересен.



Схема сборки данных моделей приводится в Приложении 5
Узловое оригами



Схема сборки данных моделей приводится в Приложении 6
Кусудамы и многогранники
Из бумаги можно построить удивительные конструкции, которые в оригами называются кусудамы, в их основе лежат правильные многогранники.
Внутри этого яркого многогранника японцы хранят сухие целебные травы. Его обычно подвешивают у постели больного. Но считается, что даже без лечебной травы этот чудо-многогранник аккумулирует космическую энергию и благотворно влияет на человека. Также кусудама передавалась из поколения в поколение как талисман и оберег семьи, как носитель положительной энергии.


Схема сборки традиционной цветочной кусудамы [6] приводится в Приложении 7
Оригами открывает невероятные широты для фантазии и творчества. Мастера из бумаги научились делать самые разнообразные поделки. Это разные животные, птицы да даже растения. Но сегодня мы подробно рассмотрим, как делать геометрические фигуры быстро и легко из бумаги.

Такие фигуры помогут развить представление о трёхмерных фигурах, а также общее представления о них. Лучше всего они подойдут тем, у кого возникают сложности с тригонометрией, так как этот раздел геометрии требует очень хорошего визуального представления разных фигур.
Мастерим куб
Итак, для сегодняшнего мастер-класса нам пригодится бумага, схемы, клей, ножницы, линейки и немножечко терпения.
Куб — самая простая фигура для оригами, простой многогранник, в котором каждая грань является квадратом. Схему для создания развертки можно распечатать на принтере, либо начертить самим. Для этого выбрать размеры граней. Ширина листа бумаги должна быть не менее 3 сторон одного квадрата, а длина не более 5 сторон. Начертить в длину листа четыре квадрата, которые станут боковыми сторонами куба. Рисовать строго на одной линии, вплотную. Над и под одним квадратом нарисовать по одному квадрату. Дорисовать полоски для склеивания, благодаря которым грани будут соединяться между собой. Наш куб уже практически готов!

Далее тонким слоем клея равномерно размазать по местам соединения. Склеить эти поверхности и закрепить на некоторое время с помощью скрепки. Клей будет схватываться около 30-40 минут. Таким образом склеить все грани.






Геометрические фигуры из бумаги: делаем поделку в технике оригами в фото
Геометрические фигуры из бумаги должен научиться делать каждый! Ведь никогда не знаешь, какие знания тебе могут пригодиться в жизни. В последнее время техника оригами набирает широкую популярность среди детей и взрослых. Но перед тем как делать разнообразные поделки (животных, птиц, растений, маленьких домиков), нужно начать с простых геометрических фигур. Такие изделия подойдут для школьников для хорошего визуального представления разных фигур.
Куб — самая простая фигура для оригами, простой многогранник, в котором каждая грань является квадратом. Схему для создания развертки можно распечатать на принтере, либо начертить самим. Для этого выбрать размеры граней. Ширина листа бумаги должна быть не менее 3 сторон одного квадрата, а длина не более 5 сторон. Начертить в длину листа четыре квадрата, которые станут боковыми сторонами куба. Рисовать строго на одной линии, вплотную. Над и под одним квадратом нарисовать по одному квадрату. Дорисовать полоски для склеивания, благодаря которым грани будут соединяться между собой. Наш куб уже практически готов!
Далее тонким слоем клея равномерно размазать по местам соединения. Склеить эти поверхности и закрепить на некоторое время с помощью скрепки. Клей будет схватываться около 30-40 минут. Таким образом склеить все грани.

Конус делается немного сложнее. Для начала нарисовать циркулем окружность. Вырезать сектор (часть кружка, ограниченная дугой окружности и двумя радиусами) из этой окружности. Острота конца конуса зависит от вырезанной части большого сектора.
Склеить боковую поверхность конуса. Далее измерить диаметр основания конуса. Циркулем нарисовать окружность на листе бумаги. Затем дорисовать треугольнички для склеивания основы с боковой поверхности. Вырезать. После приклеить основание к боковой поверхности. Поделка готова!


Параллелепипед — сложная фигура многогранник, у которого 6 граней и каждая из них параллелограмм.
Чтобы сделать параллелепипед техникой оригами, нужно начертить основание — параллелограмм любого размера. С каждой его стороны нарисовать боковые стороны — тоже параллелограммы. Далее от любой из боковых сторон дорисовать второе основание. Добавить места для склеивания. Параллелепипед может быть прямоугольным, если все стороны имеют прямые углы. Затем вырезать развертку и склеить. Готово!


Пришло время сделать пирамиду из бумаги. Это многогранник, основание которого — многоугольник, а другие грани — треугольники с общей вершиной.
Для начала нужно выбрать размеры пирамиды и количество граней. Далее нарисовать многогранник — он будет основанием. Смотря на количество граней, это может быть также треугольник, квадрат, пятиугольник.
От одной из сторон нашего многогранника нарисовать треугольник, который будет боковой стороной. Затем нарисовать еще треугольник, чтобы одна его сторона была общей с первым треугольником. Нарисовать их столько, сколько сторон в пирамиде. Далее дорисовать полоски для склеивания в необходимых местах. Вырезать и склеить фигуру. Пирамида готова!


Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.
Нарисовать прямоугольник на бумаге, в которой ширина — высота цилиндра, а длина — диаметр. Любители геометрии знают, что отношение длины прямоугольника к диаметру определяется формулой: L=nD, где L — длина прямоугольника, а D — диаметр цилиндра. С помощью этого вычисления узнать длину прямоугольника, которого будем рисовать на бумаге. Дорисовать маленькие треугольнички для склеивания деталей.
Затем нарисовать на бумаге два круга, диаметром как цилиндр. Это будет верхнее и нижнее основания цилиндра. Далее вырезать все детали. Склеить боковую поверхность цилиндра из прямоугольника. Дать детали высохнуть и приклеить к нему нижнее основание. Снова подождать, пока высохнет, и приклеить верхнюю основу. Готово!

Видео по теме статьи
Поделка посложнее
Конус делается немного сложнее. Для начала нарисовать циркулем окружность. Вырезать сектор (часть кружка, ограниченная дугой окружности и двумя радиусами) из этой окружности. Острота конца конуса зависит от вырезанной части большого сектора.
Склеить боковую поверхность конуса. Далее измерить диаметр основания конуса. Циркулем нарисовать окружность на листе бумаги. Затем дорисовать треугольнички для склеивания основы с боковой поверхности. Вырезать. После приклеить основание к боковой поверхности. Поделка готова!
Статья по теме: Варежки с орнаментом спицами: схемы с описанием и видео
Сложный параллелепипед
Параллелепипед — сложная фигура многогранник, у которого 6 граней и каждая из них параллелограмм.
Чтобы сделать параллелепипед техникой оригами, нужно начертить основание — параллелограмм любого размера. С каждой его стороны нарисовать боковые стороны — тоже параллелограммы. Далее от любой из боковых сторон дорисовать второе основание. Добавить места для склеивания. Параллелепипед может быть прямоугольным, если все стороны имеют прямые углы. Затем вырезать развертку и склеить. Готово!
Самый первый многогранник — кубик
Скорее всего, каждый человек, посещавший школу, еще в начальных классах сталкивался на уроках труда с работой, результатом которой должен был стать бумажный кубик. Чаще всего учительница раздавала заготовки — развертки многогранника куба на плотной бумаге со специальными кармашками, предназначенными для склеивания граней модели в единое целое. Такой работой ученики начальной школы могли гордиться, ведь при помощи бумаги, ножниц, клея и своих усилий получалась интересная поделка — трехмерный куб.
Пирамида-оригами
Пришло время сделать пирамиду из бумаги. Это многогранник, основание которого — многоугольник, а другие грани — треугольники с общей вершиной.
Для начала нужно выбрать размеры пирамиды и количество граней. Далее нарисовать многогранник — он будет основанием. Смотря на количество граней, это может быть также треугольник, квадрат, пятиугольник.
От одной из сторон нашего многогранника нарисовать треугольник, который будет боковой стороной. Затем нарисовать еще треугольник, чтобы одна его сторона была общей с первым треугольником. Нарисовать их столько, сколько сторон в пирамиде. Далее дорисовать полоски для склеивания в необходимых местах. Вырезать и склеить фигуру. Пирамида готова!
Интересные факты о додекаэдре
Правильные многогранники с древних времен восхищали человечество и служили прообразом мирового устройства. Как оказалось, подобные представления небезосновательны. В 2003 году, анализируя данные исследовательского аппарата WMAP, запущенного NASA для изучения фоновых космических излучений, учёные выдвинули гипотезу о додекаэдрическом строении Вселенной по принципу сферы Пуанкаре.
Игрушки древних римлян
На территориях Европы, некогда принадлежавших Римской империи, до сих пор находят загадочные бронзовые фигурки в форме додекаэдра. Предметы пустотелые, с круглыми отверстиями на каждой стороне и шариками, обозначающими вершины. Учёные пока не смогли однозначно определить функцию этих объектов. Первоначально считалось, что это своеобразные игрушки, однако позднее их отнесли к предметам культа, символизирующим устройство Вселенной. Или Земли, согласно теории, последовательно выдвигаемой с XIX века мировыми физиками, в том числе и российскими.

Впервые о том, что наша планета представляет собой кристалл додекаэдрической формы, заговорили французский математик Пуанкаре и геолог-исследователь де Бемон. Они утверждали, что земная кора, словно футбольный мяч, состоит из 12 правильных пятиугольников, в местах соединения которых, располагаются аномальные зоны и планетарные силовые поля.
В 1920-х годах идею французских коллег подхватил русский физик Степан Кислицын. Он пошёл ещё дальше, заявив, что планета не остаётся в стабильном состоянии, она растёт, из додекаэдра постепенно трансформируясь в икосаэдр. Учёный разработал модели подобных изменений, обозначив узлы гигантской кристаллической сетки, где, по его мнению, располагались месторождения полезных ископаемых: угля, нефти, газа и так далее. В 1928 году Кислицын, опираясь на свои исследования, указал на поверхности земного шара 12 алмазоносных центров, из которых 7 к настоящему времени находятся в активной разработке.

Идеи кристаллического строения планеты продолжают развиваться в XXI веке. Согласно последней гипотезе, подобная структура свойственна всем живым организмам, не только космическим телам, но и человеку. Тем интереснее будет собирать додекаэдр-оригами, чувствуя свою сопричастность к великим тайнам Вселенной.
Бумажный цилиндр
Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.
Нарисовать прямоугольник на бумаге, в которой ширина — высота цилиндра, а длина — диаметр. Любители геометрии знают, что отношение длины прямоугольника к диаметру определяется формулой: L=nD, где L — длина прямоугольника, а D — диаметр цилиндра. С помощью этого вычисления узнать длину прямоугольника, которого будем рисовать на бумаге. Дорисовать маленькие треугольнички для склеивания деталей.
Затем нарисовать на бумаге два круга, диаметром как цилиндр. Это будет верхнее и нижнее основания цилиндра. Далее вырезать все детали. Склеить боковую поверхность цилиндра из прямоугольника. Дать детали высохнуть и приклеить к нему нижнее основание. Снова подождать, пока высохнет, и приклеить верхнюю основу. Готово!
Статья по теме: Скандинавские узоры для вязания спицами со схемами и фото орнаментов
Читайте также:


