Как сделать тессеракт своими руками из бумаги
Наш проект живет и развивается для тех, кто ищет ответы на свои вопросы и стремится не потеряться в бушующем море зачастую бесполезной информации. На этой странице мы рассказали (а точнее - показали :) вам Как сделать тессеракт своими руками . Кроме этого, мы нашли и добавили для вас тысячи других видеороликов, способных ответить, кажется, на любой ваш вопрос. Однако, если на сайте все же не оказалось интересующей информации - напишите нам, мы подготовим ее для вас и добавим на наш сайт!
Если вам не сложно - оставьте, пожалуйста, свой отзыв, насколько полной и полезной была размещенная на нашем сайте информация о том, Как сделать тессеракт своими руками .
Стукнула тут меня мысль нарисовать куб в десятом измерении. Ну точнее проекцию на двухмерный экран. Думал думал думал… Ну теперь когда придумал, все кажется таким простым, но тем не менее думал я напряжно. Да и тему сначала понять надо было.
В общем что такое куб в четвертом измерении.. Будем рассматривать через проекцию на третье.
Начнем с точки. Точка вытягивается в линию Это первое измерение. Линия расползается в квадрат, второе.
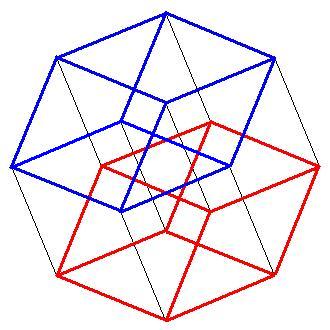
Квадрат раздваивается и расходится образуя куб.
А далее таким же методом вытягиваем куб из куба, и соединяем соответствующие точки.
Вот пример каждая точка красного куба соединена с соответствующей точкой синего.
Тессеракт
Далее идет пятое (тут я уже не стал возиться с обводкой)
Пентеракт

Хексеракт

Хептеракт

Октеракт

Энтенеракт

И десятимерный куб

Можно конечно и большие размерности и размеры (у меня тут файл 5000х5000 11мерный куб. вес правда всего 3 метра с небольшим) Но это уже если объявится желающий.
Да вот иногда я пишу подобную белеберду вместо кнопок бабло 🙂
54 thoughts on “ Тессеракт и прочие гиперкубы. ”
дружище ты бы к психологу сходил что ли 🙂
тесеракты какие то выдумываешь.
в пол седьмого утра точно бы не пошел, а вот попозжа может и прогулялся бы
Это ж надо было додуматься:) Хотя выглядит красиво, это да…
А на каком языке и с помощью каких библиотек реализовал это? Можно сделать скринсэйвер и выложить в паблик кстати.
На Делфи. рисовал стандартными процедурами на канве.
привет.
почты не нашел, а в аську по пустяку барабанить не хотеxtncz. Есть пару вопросов ричклику — судя по постам, ты с ними работаешь. Как у них с выплатами, задерживают как и сам бегун, или платят исправно как Зорька? Что нужно для аппрува, тупо дор какой-то общетематический в индексе показать, или что?
Заранее благодарен, пост можешь тереть, а ответить на почту, если не тяжело, ибо у тебя нет подписки)
Платят нормально.
Даты последних 8 платежей
20.10.2009
05.10.2009
17.09.2009
04.09.2009
19.08.2009
20.07.2009
25.06.2009
05.06.2009
Для апрува аккаунта надо показать свою вменяемость и адекватность.
Да, меня пример дора попросили показать. Спросили о трафике, о опыте, о том на каких форумах зареган и какова активность.
Уников на момент регистрации имел только 200 вместо 2к.
(Продублировал на почту)
Даже обычный гиперкуб 4-х мерный изобразить на плоскости невозможно, видел где-то в виде анимации, но все равно не то:) А то что вы изобразили это получается как бы тень от металлического каркаса таких фигур.
Я тоже видел анимацию.
Изобразить на плоскости объект большей мерности конечно невозможно. Не возможно изобразить даже обычный трехмерный куб. Поэтому изображение куба называется проекцией на плоскость.
Так и я упростил всё до плоского изображения.
Хотя если совсем точно то тут изображенны проекции на плоскость трехмерных изображений, которые получены путем проекции гиперкубов в трехмерность.
Выложи программку что ли 🙂 с исходниками
Да какие исходники.. я программированию не обучен, поэтому думаю любого человека код введет в ступор.
На крайний случай я могу описать алгоритмы в отдельном посте. В конце концов именно в алгоритмах 90% сложности этой программы.
вот это офигеть. жги еще. на самом деле. вот у меня вопрос такой: ты можешь представить это все свое творчество в объеме? просто у меня например с этим всегда были траблы.. начиная с 4-го измерения, 3-х мерное пространство — 3 взаимно-перпендикулярных координатных оси, 4-х мерное пространство 4 оси. Куда ее пристроить-то? Ты я смотрю просто берешь и смещаешь трехмерный куб в разных направлениях, т.е каждая последующая мерность — реализуется виде некоторого движения. Это здорово, но все таки не то. В итоге получаешь просто траекторию движения точек куба, чем больше направлений смещения берешь,тем больше размерность. Однако, навряд ли это именно то, что происходит в действительности. Напиши, что думаешь по этому поводу.
Виноват. Вот перечитал пост свой. Все верно. Натупил слегка. Не о том подумал.
По факту это все проекции на третье измерение.
Думаю представить четвертое геометрическое пространство можно только абстрактно, но не визуально. Так как визуально все упирается в 2 и 3 мерность.
И даже если вспомнить разбитие на плоскости как это было в черчении, то трехмерный объект это просто три плоскости. А четырехмерный значит 4 объемности. (Смотря с каждой из четырех мерностей мы будем видеть трехмерный объект) формально четырехмерный объект будет описан, но чтобы представить его нужно иметь другой мозг.
И каждое новое смещение можно рассматривать как представление новой грани.. То есть мы копируем объект придавая ему еще одну глубину, будто бы мы посмотрели на объект с такого ракурса где видна новая ось. Но эти новые грани будут изначально трехмерными проекциями.
Если отойти от условностей и сделать многомерный куб в третьем измерении, то это будет тот же самые трехмерный куб, потому что для человеческого мозга не существует 4 геометрического измерения… Это как если бы человек из плоскости смотрел на куб, то он видел бы только квадрат.
Можно представить четвертое измерение как плоский срез пространства, имеющий глубину. Но это опять же проекция третьего измерения, где глубину третьего измерения подменяют глубиной четвертого.
Я вообще как то заморочился с перелинковкой сетки сателлитов в 400 штук такою штуку навоял парни долго потом всматривались в итоге сказали что надо лечиться,сейчас эта перелинковка цветет и процветает.
Извини за офтоп!!Но твои фигуры просто мне напомнили это!
Автор? ты что фентези перечитал? ил переиграл малость?
Отвечу на вопросы по очереди.
Автор
Перечитал
Переиграл
🙂
Мне думается что тесеракт- это просто невозможная фигура, как например треугольник из брусков у которого все углы по 90 градусов, просто интересная безделушка. А 4-ое измерение это из научной фантастики, одни лишь теории.
Да фигура невозможная, потому что человек не способен воспринимать 4 геометрическое измерение.
По повожу фантастики.
Когда программисты задают массив, они вполне могут сделать его четырех, пяти и более мерным.
третье измерение глубина.
На плоскости мы будем видеть ширину и высоту, достаточно чтобы построить квадрат.
Если нарисовать на листе человечка и рядом квадрат, то конечно он его увидит как линию. Но как мы смотрим на плоскость (ведь изображение просто проецируется на сетчатке) и уже потом додумываем объем, так и он имея две оси вполне сможет понять, что перед ним квадрат.
И мне кажется обсуждение ушло куда то не туда.
Еще раз повторюсь это просто геометричекие проекции.
если нет высоты то, тогда есть ширина и глубина. В любом случае есть два измерения а их достаточно для квадрата, на то она и плоскость.
Так же как и мы видим плоские объекты а не объемные. Но без всяких проблем рассуждаем о объеме.
Поэтому я и говорил о высоте. он же своими глазами не только вперед-назад смотрит, но и вверх-вниз
тем не менее Penteract и Septeract существуют в виде матеиатических констант.
всё же, нарисовать 4х мерный объект в 3х мерном виде и поместить на 2х мерный экран, всё равно мы увидим не то, даже если предположить существование четвертого измрения
Вы всерьез думаете, что я не видел те картинки?
Мои картинки имеют равные грани, те — нет. Приглядитесь.
класс. молодец. а то народ совсем тупой
К тому же, так как я не рисовал их, а программировал, то мне тоже было нужно разработать универсальный метод построения, с чем я справился. И даже если бы не справился, то все равно думал бы сам, потому, что именно в этом и заключается смысл тренировки. В том, чтобы решить задачу самостоятельно.
Однако, если хотите, я могу сделать ссылку на вашу работу. Интересующиеся смогут ее скачать и прочитать.
Кроме того, вы упомянули трехмерные проекции. Если у вас есть фотографии, то их тоже можно опубликовать. Думаю они заинтересуют всех, кто сюда заходит.
Хотите так?
Спасибо, что ответили. Всего Вам самого доброго.
С уважением,
Михайлова Людмила Михайловна.
Разработка возникла во многом благодаря и Вашей, Elsper, тематической компиляции, за что особое Вам большое спасибо. :)))
Возможно, в случае знакомства, возникнут мобильные конструктивы по дальнейшему развитию идеи освоения многомерных пространства — искренне будем благодарны за любые интересные мысли в данном направлении.
С уважением, Stellari.stA.G
Приятно, что мои работы служат не только мне. )
Правда сейчас меня интересуют совсем другие вопросы.
В геометрии гиперкуб - это n-мерная аналогия квадрата (n = 2) и куба (n = 3). Это замкнутая выпуклая фигура, состоящая из групп параллельных линий, расположенных на противоположных краях фигуры, и соединенных друг с другом под прямым углом.
Эта фигура также известная под названием тессеракт (tesseract). Тессеракт относится к кубу, как куб относится к квадрату. Более формально, тессеракт может быть описан как правильный выпуклый четырехмерный политоп (многогранник), чья граница состоит из восьми кубических ячеек.
Согласно Окфордскому словарю английского языка, слово "tesseract" было придумано в 1888 Чарльзом Говардом Хинтоном (Charles Howard Hinton) и использовано в его книге "Новая эра мысли" ("A New Era of Thought"). Слово было образовано от греческого "τεσσερες ακτινες" ("четыре луча"), имеется в виде четыре оси координат. Кроме этого, в некоторых источниках, эту же фигуру называли тетракубом (tetracube).
n-мерный гиперкуб также называется n-кубом.
| Проекция гиперкуба на плоскость |
Точка - это гиперкуб размерности 0. Если сдвинуть точку на единицу длины, получится отрезок единичной длины - гиперкуб размерности 1. Далее, если сдвинуть отрезок на единицу длины в направлении перпендикулярном направлению отрезка получится куб - гиперкуб размерности 2. Сдвигая квадрат на единицу длины в направлении перпендикулярном плоскости квадрата, получается куб - гиперкуб размерности 3. Этот процесс может быть обобщен на любое количество измерений. Например, если сдвинуть куб на единицу длины в четвертом измерении, получится тессеракт.
Семейство гиперкубов является одним из немногих правильных многогранников, которые могут быть представлены в любом измерении.
Элементы гиперкуба
Гиперкуб размерности n имеет 2n "сторон" (одномерная линия имеет 2 точки; двухмерный квадрат - 4 стороны; трехмерный куб - 6 граней; четырехмерный тессеракт - 8 ячеек). Количество вершин (точек) гиперкуба равно 2 n (например, для куба - 2 3 вершин).
Количество m-мерных гиперкубов на границе n-куба равно
Например, на границе гиперкуба находятся 8 кубов, 24 квадрата, 32 ребра и 16 вершин.
Проекция на плоскость
Формирование гиперкуба может быть представлено следующим способом:
- Две точки A и B могут быть соединены, образуя отрезок AB.
- Два параллельных отрезка AB и CD могут быть соединены, образуя квадрат ABCD.
- Два параллельных квадрата ABCD и EFGH могут быть соединены, образуя куб ABCDEFGH.
- Два параллельных куба ABCDEFGH и IJKLMNOP могут быть соединены, образуя гиперкуб ABCDEFGHIJKLMNOP.
Последнюю структуру нелегко представить, но возможно изобразить ее проекцию на двухмерное или трехмерное пространство. Более того, проекции на двухмерную плоскость могут быть более полезны возможностью перестановки позиций спроецированных вершин. В этом случае можно получить изображения, которые больше не отражают пространственные отношения элементов внутри тессеракта, но иллюстрируют структуру соединений вершин, как на примерах ниже.
На первой иллюстрации показано, как в принципе образуется тессеракт путем соединения двух кубов. Эта схема похожа на схему создания куба из двух квадратов. На второй схеме показано, что все ребра тессеракта имеют одинаковую длину. Эта схема также заставляют искать соединенные друг с другом кубы. На третьей схеме вершины тессеракта расположены в соответствии с расстояниями вдоль граней относительно нижней точки. Эта схема интересна тем, что она используется как базовая схема для сетевой топологии соединения процессоров при организации параллельных вычислений: расстояние между любыми двумя узлами не превышает 4 длин ребер, и существует много различных путей для уравновешивания нагрузки.
| Развертка тессеракта |
Развертка гиперкуба
Тессеракт может быть развернут в восемь кубов, подобно тому как куб может быть развернут в шесть квадратов. Многогранник-равертка гиперкуба называется сетью. Существует 261 различных вариантов сетей. Справа показан один из вариантов
 Сальвадор Дали "Распятие" (1954) |
Гиперкуб в искусстве
Гиперкуб появился в научно-фантастической литературе с 1940 года, когда Роберт Хайнлайн в рассказе "Дом, который построил Тил" ("And He Built a Crooked House") описал дом, построенный по форме развертки тессеракта. В рассказе этот Далее этот дом сворачивается, превращаясь в четырехмерный тессеракт. После этого гиперкуб появляется во многих книгах и новеллах.
В фильме "Куб 2: Гиперкуб" рассказывается о восьми людях, запертых в сети гиперкубов.
На картине Сальвадора Дали "Распятие" ("Crucifixion (Corpus Hypercubus)", 1954) изображен Иисус распятый на развертке тессеракта. Эту картину можно увидеть в Музее Искусств (Metropolitan Museum of Art) в Нью-Йорке.
Заключение
Гиперкуб - одна из простейших четырехмерных объектов, на примере которого можно увидеть всю сложность и необычность четвертого измерения. И то, что выглядит невозможным в трех измерениях, возможно в четырех, например, невозможные фигур. Так, например, бруски невозможного треугольника в четырех измерениях будут соединены под прямыми углами. И эта фигура будет выглядеть так со всех точек обзора, и не будет искажаться в отличие от реализаций невозможного треугольника в трехмерном пространстве (см. "Невозможные фигуры в реальном мире").
--> FISHKINET

ЧУДО психоанализа: заработать на модных профессиях не прочь даже бывший священник



7 главных достижений гениального конструктора Сергея Королева

Очень редкий и броский кабриолет Mercedes-Benz CLK DTM AMG


Нетрезвая автомобилистка завалилась на бок в Новосибирске

В Тимашевске инвалид сам почистил снег, чтобы проехать

Когда выгорание подкралось незаметно: с юмором о модном нынче термине

"Ошалели!": в Приморском крае мужчина устал от драки соседей и бросил в них гранату

Redkey W12: беспроводный пылесос, который не только пылесосит, но и моет пол
Как создать идеальный профиль на сайте знакомств и не ударить в грязь лицом



"Без медовухи не обойтись": как прошла встреча Путина со студенческим братством



После государственного переворота жители Буркина-Фасо вышли на улицы с российскими флагами

Короткий разговор с мошенником, притворяющимся полицейским

Грозившийся спрыгнуть с Крымского моста мужчина оказался мигрантом

Авария дня. В Томской области в ДТП погибла пассажирка китайского хэтчбека



Рождённый не плавать: зачем в США строили корабли, которые никогда не спускали на воду
Боль и разорение: как обстоят дела у начинающих инвесторов

Блогерша показала удачные позы для женской фотосессии

Фильмы, в которых для создания массивных сооружений использовались миниатюры


В сети появилось видео собаки, привязанной цепью к грузовику, взволновавшее зоозащитников


Как сделать уличный холодильник из подручных материалов

Эти вещи объединили в себе и абсолютно безумную задумку, и идеальное воплощение

Сильные в своей слабости, слабые в своей силе: о женщинах в армиях мира



Возвращение 90-х: в Калмыкии похищенного московского бизнесмена подвергли пыткам

Зажигалка неожиданно взорвалась в руках курильщика

В Австрии мигрант из Армении напал на женщину с ножом



Audi Rosemeyer — неповторимый и концептуальный суперкар 2000 года


Дочери в отместку обвинили парня в педофилии, а их сидевший отец его пытался зарезать

В Анапе таксист обиделся на клиента за ожидание и, покатав по городу, привез его назад к дому

Ferrari 308 GTSi 1982 года — действительно особенная находка в сарае




Квартиры для детей: канадец создает игровые домики со всеми удобствами настоящих жилищ
Читайте также:


