Как напечатать степень числа на клавиатуре в паскале
Программирование. Стандартные функции Pascal-Паскаль
- Скачено бесплатно: 18563
- Куплено: 414
-
->Программирование. Стандартные функции Pascal-Паскаль
Стандартные функции Pascal-Паскаль
| Стандартные математические функции Турбо Паскаля | |||
|---|---|---|---|
| Обращение | Тип аргумента | Тип результата | Примечание |
| Abs(x) | Real, integer | Тип аргумента | Модуль аргумента |
| ArcTan(x) | Real, integer | Real | Арктангенс (значение в радианах) |
| Cos(x) | Real, integer | Real | Косинус, угол в радианах |
| Exp(x) | Real, integer | Real | Экспонента |
| Frac(x) | Real | Real | Дробная часть числа |
| Int(x) | Real, integer | Real | Целая часть числа |
| Ln(x) | Real, integer | Real | Логарифм натуральный |
| Pi | Нет | Real | 3,141592653 |
| Sin(x) | Real, integer | Real | Синус, угол в радианах |
| Sqr(x) | Real, integer | Тип аргумента | Квадрат аргумента |
| Sqrt(x) | Real, integer | Real | Корень квадратный |
| Random | Нет | Real | Псевдослучайное число в интервале [0, 1] |
| Random(I) | Integer | Integer | Псевдослучайное число в интервале [0, I] |
| Round(x) | Real | Integer | Округление до ближайшего целого |
| Trunc(x) | Real | Integer | Отбрасывание дробной части числа |
Порядок вычислений в выражениях следующий:
- вычисляются подвыражения, заключенные в скобки;
- затем выполняются операции с наибольшим приоритетом; обычно используются следующие уровни приоритетов (в порядке убывания):
- возведение в степень;
- мультипликативные операции: * , / , div , mod;
- унарные операции: + , - , abs , not;
- аддитивные операции: +, -;
- операции отношения: = , <>, <, >, <=, >=;
- логические операции: and, or, not;
- операции с одинаковым приоритетом выполняются слева направо.
Хотя нет ограничений на сложность выражений, однако выражения, содержащие более 7 операндов, трудны для чтения и понимания и поэтому такие выражения не рекомендуется использовать.
Замечание (это важно!)
- в Паскале нет стандартной операции или стандартной функции возведения в степень, поэтому используется следующее математическое тождество: x y = e ylnx
- в Паскале существует только стандартная функция вычисления натурального логарифма, поэтому используется следующее математическое тождество: logab= ln b/ln a
Математическое выражение: x 3/2 - 7x + tg (x+2)
Выражение на Паскале: exp(3*ln(x)/2)-7*x+sin(x+2)/cos(x+2)
Операторы действия
Операторы действия - это средства языка, позволяющие изменять в процессе выполнения программы состояние вычислений. Самый простой оператор действия - оператор присваивания.
Пример оператора присваивания
Оператор присваивания, несмотря на кажущуюся простоту, имеет очень важное алгоритмическое значение.
Удобно считать, что выполнение присваивания переменной некоторого значения означает помещение этого значения в выделенный для переменной ящик. При этом каждый запоминающий ящик обладает следующими свойствами.
- В каждый момент времени в ящике может храниться не более одного значения.
- Каждый ящик способен хранить только значения одного и того же типа. Попытка поместить в ящик значение любого другого типа приводит к тому, что ящик отказывается принимать на хранение передаваемое ему значение - это расценивается как ошибка в программе.
- Значение, помещенное в ящик, будет храниться в нем до тех пор, пока в этот ящик не будет помещено новое значение (в момент присваивания соответствующей переменной этого нового значения) - при этом предыдущее содержимое ящика безвозвратно теряется (уничтожается).
- Находящееся в ящике значение считается текущим значением соответствующей переменной. Это текущее значение может быть выдано из ящика для использования сколько угодно раз, но при этом содержимое ящика не меняется: из него каждый раз выдается копия хранящегося значения с сохранением оригинала в ящике без какого-либо изменения.
- К началу выполнения программы содержимое всех запоминающих ящиков считается неопределенным; в частности, их нельзя считать и пустыми, поскольку эти ящики могли использоваться при выполнении предыдущих программ, после чего в ящиках могло что-то остаться.
Еще один оператор действия, хотя его можно лишь условно назвать таковым: он не выполняет никакого действия, это - пустой оператор (в Паскале он обознается знаком ";"). В Паскале оператором действия является также оператор процедуры. Последний из простейших операторов действия - оператор останова, который прерывает работу программы (в Паскале это оператор halt).
Ввод и вывод данных
Ввод данных с клавиатуры производится с помощью стандартной процедуры read( ) или ее разновидности readln( ). Элементы списка ввода - идентификаторы (имена) переменных, перечисляемые через запятую. При выполнении этого оператора пользователь набирает на клавиатуре соответствующую последовательность значений, разделяя их пробелами (это важно!).
Пример ввода данных с клавиатуры
read(a,b,c);
readln(a,b,c);
Вывод данных на экран производится с помощью стандартной процедуры write( ) или ее разновидности writeln( ).
Список вывода может содержать константы, переменные, выражения, формат вывода. Выражения в списке вывода разделяются запятыми.
Пример вывода данных на экран
write(a,b,c);
writeln(a,b,c);
Окончание ln в имени процедуры означает, что курсор автоматически будет переведен в начало следующей строки экрана.
Программирование
Исходники Pascal (127)
Справочник
Справочник по паскалю: директивы, функции, процедуры, операторы и модули по алфавиту
Как известно, ядро Паскаля предельно компактно, и многие математические функции в модуле System просто отсутствуют. Поэтому у людей, изучающих основы программирования именно на этом языке, типовые математические расчёты зачастую вызывают проблемы. Далее приводятся пути решения наиболее типичных из этих проблем.
Возведение в произвольную степень на Паскале
Требуется вычислить значение с = a b . В зависимости от значений основания a и показателя степени b , вычисление степени может быть реализовано по-разному.
Если a > 0 , а b может принимать произвольные вещественные значения, используем известную формулу a b = exp (b * ln a) :
Если b - целое число (вообще говоря, "не слишком большое" по модулю), а a - любое (не равное нулю при b < 0 ), возведение в степень может быть реализовано с помощью цикла:
Для целого b и не равного нулю a выгоднее считать с помощью экспоненты и логарифма, не забывая о том, что не существует логарифмов от отрицательных чисел:
Вычисление корня произвольной степени на Паскале
Стандартная функция sqrt умеет извлекать только квадратный корень.
Извлечь корень степени n (где n - натуральное) из числа a можно всегда, кроме случая, когда a < 0 и при этом n четно. Извлечь корень степени n из числа a означает возвести число a в степень 1/n . При этом знак корня совпадает со знаком a . Ниже приводится код функции, вычисляющей корень произвольной степени n от своего аргумента a :
Вычисление логарифмов на Паскале
Стандартная функция ln вычисляет только натуральный логарифм. Для вычисления логарифмов по другим основаниям можно применить формулу log a b = ln b / ln a :
В частности, для вычисления десятичного логарифма lg b можно записать:
Вычисление обратных тригонометрических функций (арксинусов и арккосинусов) на Паскале
В Паскале имеется стандартная функция arctan для вычисления арктангенса.
Другие обратные тригонометрические функции могут быть выражены через неё с помощью формул тригонометрии.
Для вычисления y = arcsin x , где, конечно, |x| <= 1 , можно применить один из следующих способов:
на практике следует помнить о возможных погрешностях при сравнении вещественных чисел (глава учебника, п.7.2).
Для вычисления z = arccos x , где |x| <= 1 , можно использовать тот факт, что сумма арксинуса и арккосинуса некоторого значения равна прямому углу:
Вычисление полярных углов на Паскале
Полярным углом точки с координатами (x,y) , отличной от начала координат, называют угол между положительным направлением оси Ox и направлением из начала координат на данную точку. При этом угол отсчитывается против часовой стрелки. Строго говоря, полярный угол не всегда равен arctg (y/x) , это верно лишь при x > 0 . Кроме того, при делении большого значения y на малое x возможно переполнение. Показанная ниже функция вычисляет полярный угол fi , лежащий в промежутке от -pi до +pi , для любой точки с координатами (x,y) , не совпадающей с началом координат:
Проблема с приведением типов на Паскале
Начинающие "паскалисты" нередко не понимают строгой типизированности этого языка, из-за чего находят в нём несуществующие "баги". Вот простейший пример.
Эта программа выдаст отнюдь не 200000, как может показаться. Ответ будет равен 3392 (результат переполнения). Никакого бага нет. Тип выражения в Паскале определяется только типом входящих в него переменных, но не типом переменной, куда записывается результат. То есть, мы вычислили с переполнением произведение двух переменных типа Integer , а потом "испорченный" результат переписали в переменную типа Longint . ничего не изменит и
Здесь тоже сначала вычислен результат с переполнением, затем преобразован к типу Longint . А вот
рулит, получите свои 200000 :) Указанная ошибка часто встречается в программах начинающих. Чтобы её не повторять, помните - выражение в Паскале должно быть приведено к нужному типу в процессе его вычисления, а не после его окончания или при присваивании.
Нередко мы сталкиваемся с тем, что нам необходимо возвести число в какую-либо степень. Можно воспользоваться обычным калькулятором. Но это неинтересно и очень часто не подходит под условия поставленной задачи.
Понятие степени в математике
Стоит начать с пояснения математического смысла возведения в степень. Например, нам необходимо возвести некоторое число x в степень y. В математике эта запись выглядела бы так: x y = x ^ y. Это означает, что число x нужно умножить на себя y раз. Помните: какое бы вы число ни возводили в нулевую степень, получится единица, а также при возведении в первую степень мы получим наше исходное число. При возведении в отрицательную степень мы всего лишь переворачиваем полученный результат.
Возведение в степень на паскале
С математикой всё понятно. Но как же нам сделать такую программу, которая будет производить возведение в степень? Тут всё просто. Если нам необходимо возвести x в степень 5, то наш код примет вид: res:= x * x * x * x * x. Мы умножили число x на себя 5 раз, как нам и было необходимо, но что делать, если нам не известна степень, в которую необходимо возвести число? Далее мы рассмотрим, как производить возведение в степень. Паскаль предоставляет нам не очень много возможностей для этого, но мы обязательно что-нибудь придумаем. Например, использование стандартных функций и процедур или использование различных циклов.
Возведение числа в квадрат
Начнём, пожалуй, с возведения в квадрат. Возведение в квадрат является частным случаем возведения в степень. Для этого в паскале предусмотрена стандартная процедура sqr(x). Она возведёт наше число x в квадрат, эта запись равна записи x*x.

Очень часто этого вполне достаточно, но не всегда программа может ограничиться одним лишь возведением в квадрат. Как же возводить в более высокие степени? Об этом читаем далее и просвещаемся.
Использование стандартных операторов
В паскале существует два метода для возведения числа в степень: exp(ln(x)*y) и метод power(x, y). Процедура exp() имеет ограничение: x должно быть больше 0, т.к. нельзя извлечь натуральный логарифм из неположительного числа, но эта функция считается устаревшей и неудобной для использования, поэтому дальше мы о ней говорить не будем. Функция power() принимает два значения, первое число (x) - которое нужно возвести в степень, второе число (y) - степень, в которую нужно возвести и возвращает x в степени y. Следует помнить, что числа х и у - вещественные, то есть типа real.

Но тут есть один недостаток, эта функция есть не во всех версиях паскаля. Да и вообще, иногда возведение в степень должно производиться без использования операторов. Идём дальше и разбираем следующий способ.
Возведение в степень при помощи цикла for
Как мы уже поняли, возведение числа в степень - это последовательное умножение числа на само себя несколько раз. Повторить какое-то действие несколько раз в программировании гораздо легче, чем в жизни. Воспользуемся циклом for:

Разберемся, что и как тут работает. Для начала мы вводим два числа: x и y. Затем берём за результат единицу, для чего это - ниже. Выполняем цикл до модуля нашей степени, т.к. если степень будет отрицательной, то цикл не пойдёт. В цикле мы умножаем наш результат на само число x. Так зачем мы присваивали результату 1? Во-первых, если бы мы умножали на 0, то программа всегда выдавала бы 0. Во-вторых, наша степень может быть равна 0, тогда программа должна вернуть нам 1, т.к. любое число в 0 степени это 1. Затем мы проверяем, является степень отрицательным числом или положительным: если она отрицательна, то делим единицу на наш результат. Выполнение этой задачи при помощи цикла while делается почти так же.
Использование цикла while при возведении в степень
Использование цикла while более правильно, нежели for, но для понимания проще предыдущий вариант. Вряд ли можно стоит ограничиваться одним лишь циклом for, для понимания будет лучше посмотреть несколько примеров, да и задача бывает поставлена по-разному, кому-то одним циклом, кому-то другим, именно поэтому мы разберём ещё один способ возведения в степень.

Всё почти так же, как и раньше. Вводим два числа х и у. Присваиваем нашему результату значение единицы, чтобы возводить в нулевую степень. Затем создаём счётчик i и присваиваем ему значение модуля нашей степени. Цикл идёт до тех пор, пока счётчик не равен нулю, если степень с самого начала равна нулю, то цикл не будет выполняться, результат так и останется единицей, как и должно быть, ведь любое число в нулевой степени - это единица. В самом цикле мы всё так же считаем результат, умножая уже полученный результат на наше число х, не забываем вычитать из нашего счётчика единицу, иначе мы никогда не дойдём до нуля. Ну а затем так же, как выше, преобразование, если степень была отрицательной. Ничего сложного, как оказалось. Впрочем, никто и не сомневался.
Что же, с обычными числами мы закончили, но ведь есть не только такие числа.
Понятие комплексных чисел
Нам с самого начала школьного обучения объясняют только обычные числа, но есть ведь ещё и другие, например, комплексные числа. Они довольно сложны в представлении, особенно учитывая то, что нас почти нигде не знакомят с ними. В математической записи они имеют вид z = x + yi, где x и y - это некоторые числа, а i - мысленная единица. Вы сразу подумали: да это же обычное число, стоит просто провести операцию сложения. Но нет, не всё так просто. Это не сумма, это именно число. Другими словами, если попытаться представить это всё с точки зрения геометрии, то можно заменить знак сложения точкой с запятой, и получатся как бы координаты точки, x и y. И если построить нулевой вектор до этой точки, то мы сможем визуально увидеть всё это. Кажется, текста стало слишком много, давайте немного посмотрим:
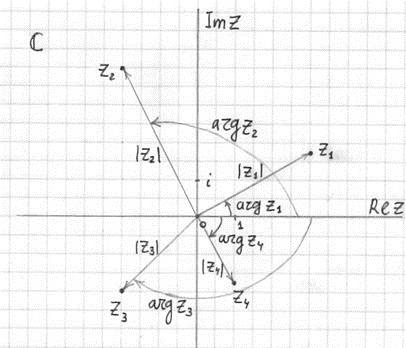
Если мы хотим показать, что наша плоскость комплексная, достаточно пометить её жирной буквой C, как тут. Затем мы можем видеть множество точек, давайте посмотрим на них и попытаемся понять, какая из них как записывается. Берём точку z1, опускаем проекцию на ось ReZ и получаем 3, затем на ось lmZ и получаем 1,75, в итоге имеем число z1=3 + 1.75i. Вроде всё понятно, давайте ещё раз, для закрепления. Точка z2, по горизонтальной оси - два, по вертикальной - четыре, в итоге имеем: z2=2 + 4i. Всё предельно понятно и просто.
С комплексными числами возможны все те же операции, что и с обычными. Сложение, вычитание, умножение, деление. Но в этой статье мы подробно остановимся на возведении комплексного числа в степень.
Возведение в степень комплексного числа
Что делать, если нужно возвести в степень комплексное число? Не паникуйте! Всё точно так же, как с обычными числами, но чуточку сложнее. Начнём с квадрата. Дано число z = 2 + 5i. Возводим в квадрат, получаем z 2 = (2 + 5i) 2 = (2 + 5i)(2 + 5i) - а это обычный двучлен, можно просто перемножить, привести подобные слагаемые и всё. Это очень просто, но что делать, когда нужно возвести в более высокую степень? Для начала следует представить наше число в тригонометрической форме, например:
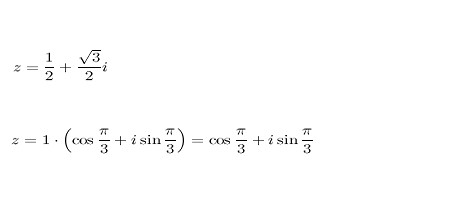
Затем необходимо воспользоваться формулой возведения комплексных чисел в тригонометрической форме: z n =|z| n * (cos(nx) + i * sin(nx)). Можно заметить, что при возведении комплексных чисел даже в очень большие степени они сильно не изменяются, так что не пугайтесь, это сложно, но с практикой всё придёт.
Таким образом, теперь вы знаете, как возводить числа в степень в математике, на языке программирования паскаль, также узнали, что такое комплексные числа и как их возводить в степень. Всё оказалось куда проще, чем вы думали. Не так ли? Остаётся лишь попробовать всё на своём опыте, и всё встанет на свои места. Любая задача, связанная с возведением в степень, теперь решается очень легко для вас.
Программирование. Стандартные функции Pascal-Паскаль
- Скачено бесплатно: 18563
- Куплено: 414
-
->Программирование. Стандартные функции Pascal-Паскаль
Стандартные функции Pascal-Паскаль
| Стандартные математические функции Турбо Паскаля | |||
|---|---|---|---|
| Обращение | Тип аргумента | Тип результата | Примечание |
| Abs(x) | Real, integer | Тип аргумента | Модуль аргумента |
| ArcTan(x) | Real, integer | Real | Арктангенс (значение в радианах) |
| Cos(x) | Real, integer | Real | Косинус, угол в радианах |
| Exp(x) | Real, integer | Real | Экспонента |
| Frac(x) | Real | Real | Дробная часть числа |
| Int(x) | Real, integer | Real | Целая часть числа |
| Ln(x) | Real, integer | Real | Логарифм натуральный |
| Pi | Нет | Real | 3,141592653 |
| Sin(x) | Real, integer | Real | Синус, угол в радианах |
| Sqr(x) | Real, integer | Тип аргумента | Квадрат аргумента |
| Sqrt(x) | Real, integer | Real | Корень квадратный |
| Random | Нет | Real | Псевдослучайное число в интервале [0, 1] |
| Random(I) | Integer | Integer | Псевдослучайное число в интервале [0, I] |
| Round(x) | Real | Integer | Округление до ближайшего целого |
| Trunc(x) | Real | Integer | Отбрасывание дробной части числа |
Порядок вычислений в выражениях следующий:
- вычисляются подвыражения, заключенные в скобки;
- затем выполняются операции с наибольшим приоритетом; обычно используются следующие уровни приоритетов (в порядке убывания):
- возведение в степень;
- мультипликативные операции: * , / , div , mod;
- унарные операции: + , - , abs , not;
- аддитивные операции: +, -;
- операции отношения: = , <>, <, >, <=, >=;
- логические операции: and, or, not;
- операции с одинаковым приоритетом выполняются слева направо.
Хотя нет ограничений на сложность выражений, однако выражения, содержащие более 7 операндов, трудны для чтения и понимания и поэтому такие выражения не рекомендуется использовать.
Замечание (это важно!)
- в Паскале нет стандартной операции или стандартной функции возведения в степень, поэтому используется следующее математическое тождество: x y = e ylnx
- в Паскале существует только стандартная функция вычисления натурального логарифма, поэтому используется следующее математическое тождество: logab= ln b/ln a
Математическое выражение: x 3/2 - 7x + tg (x+2)
Выражение на Паскале: exp(3*ln(x)/2)-7*x+sin(x+2)/cos(x+2)
Операторы действия
Операторы действия - это средства языка, позволяющие изменять в процессе выполнения программы состояние вычислений. Самый простой оператор действия - оператор присваивания.
Пример оператора присваивания
Оператор присваивания, несмотря на кажущуюся простоту, имеет очень важное алгоритмическое значение.
Удобно считать, что выполнение присваивания переменной некоторого значения означает помещение этого значения в выделенный для переменной ящик. При этом каждый запоминающий ящик обладает следующими свойствами.
- В каждый момент времени в ящике может храниться не более одного значения.
- Каждый ящик способен хранить только значения одного и того же типа. Попытка поместить в ящик значение любого другого типа приводит к тому, что ящик отказывается принимать на хранение передаваемое ему значение - это расценивается как ошибка в программе.
- Значение, помещенное в ящик, будет храниться в нем до тех пор, пока в этот ящик не будет помещено новое значение (в момент присваивания соответствующей переменной этого нового значения) - при этом предыдущее содержимое ящика безвозвратно теряется (уничтожается).
- Находящееся в ящике значение считается текущим значением соответствующей переменной. Это текущее значение может быть выдано из ящика для использования сколько угодно раз, но при этом содержимое ящика не меняется: из него каждый раз выдается копия хранящегося значения с сохранением оригинала в ящике без какого-либо изменения.
- К началу выполнения программы содержимое всех запоминающих ящиков считается неопределенным; в частности, их нельзя считать и пустыми, поскольку эти ящики могли использоваться при выполнении предыдущих программ, после чего в ящиках могло что-то остаться.
Еще один оператор действия, хотя его можно лишь условно назвать таковым: он не выполняет никакого действия, это - пустой оператор (в Паскале он обознается знаком ";"). В Паскале оператором действия является также оператор процедуры. Последний из простейших операторов действия - оператор останова, который прерывает работу программы (в Паскале это оператор halt).
Ввод и вывод данных
Ввод данных с клавиатуры производится с помощью стандартной процедуры read( ) или ее разновидности readln( ). Элементы списка ввода - идентификаторы (имена) переменных, перечисляемые через запятую. При выполнении этого оператора пользователь набирает на клавиатуре соответствующую последовательность значений, разделяя их пробелами (это важно!).
Пример ввода данных с клавиатуры
read(a,b,c);
readln(a,b,c);
Вывод данных на экран производится с помощью стандартной процедуры write( ) или ее разновидности writeln( ).
Список вывода может содержать константы, переменные, выражения, формат вывода. Выражения в списке вывода разделяются запятыми.
Пример вывода данных на экран
write(a,b,c);
writeln(a,b,c);
Окончание ln в имени процедуры означает, что курсор автоматически будет переведен в начало следующей строки экрана.
Программирование
Исходники Pascal (127)
Справочник
Справочник по паскалю: директивы, функции, процедуры, операторы и модули по алфавиту
Читайте также:


