Зависимость сопротивления металлических проводников от температуры используется в
Зависимость сопротивления проводника от температуры
Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что
- возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
- изменяется их концентрация при нагревании проводника.
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:
\(~\rho_t = \rho_0 (1 + \alpha t) ,\) \(~R_t = R_0 (1 + \alpha t) ,\)
где ρ0, ρt — удельные сопротивления вещества проводника соответственно при 0 °С и t °C; R0, Rt — сопротивления проводника при 0 °С и t °С, α — температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К -1 ). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Температурный коэффициент сопротивления вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.
где \(~\mathcal h \alpha \mathcal i\) — среднее значение температурного коэффициента сопротивления в интервале ΔΤ.
Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. У чистых металлов α = 1/273 К -1 . У металлов концентрация свободных носителей зарядов (электронов) n = const и увеличение ρ происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.
Формулы зависимости ρ и R от температуры для электролитов аналогичны приведенным выше формулам для металлических проводников. Необходимо отметить, что эта линейная зависимость сохраняется лишь в небольшом диапазоне изменения температур, в котором α = const. При больших же интервалах изменения температур зависимость сопротивления электролитов от температуры становится нелинейной.
Графически зависимости сопротивления металлических проводников и электролитов от температуры изображены на рисунках 1, а, б.
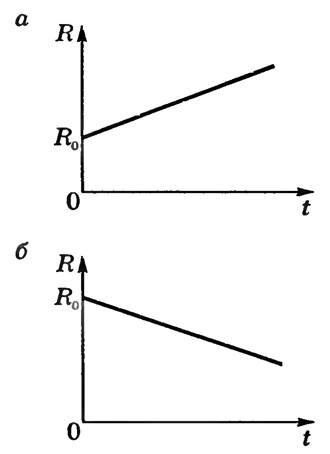
При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости. Металл переходит в сверхпроводящее состояние.
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена.
Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 256-257.
Проект по физике «Исследование зависимости электрического сопротивления проводника от температуры» (9 класс)
Основным законом электротехники, при помощи которого можно изучать и рассчитывать электрические цепи, является закон Ома, устанавливающий соотношение между током, напряжением и сопротивлением. Необходимо отчетливо понимать его сущность и уметь правильно пользоваться им при решении практических задач. Часто в электротехнике допускаются ошибки из-за неумения правильно применить закон Ома.
Данная исследовательская работа служит дополнением расширяющие рамки школьной программы, и посвящена закону Ома и температурному коэффициенту. Выбор темы не случаен, основным поводом послужило, что на практике при использовании ламп накаливания в цепи, при увеличение напряжения на лампе например в два раза не приводит к увеличению тока в два раза, как мы уже знаем данное условие противоречит выполняемости закона Ома. Значит -закон Ома не всегда справедлив. Хотим заметить, в школьном курсе физики данному моменту не уделено должного внимания.
В этой связи весьма важным представляется проанализировать перечисленных выше фактов и выявить решение проблемы, как методом изучения дополнительной литературы, так и рассмотреть практически. Такова цель настоящей работы.
Выявить влияние фактора температуры проводника на его электрическое сопротивление и соблюдение выполнения закона Ома от данного обстоятельства.
Объектом исследования является определяющая связь электрического напряжения с силой тока, протекающего в проводнике, и сопротивлением проводника, и его температурой.
Методы исследования:
Практическая значимость работы заключается в дополнительном представлении учащимся, что закон Ома не является фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников, но перестающим соблюдаться в ряде ситуаций.
1. Зависимость сопротивления металлических проводников от температуры.
1.1 История происхождения закона Ома
Большой в клад в формирование взаимосвязи силы тока, напряжения и сопротивление проводника внес немецкий физик Георг Симон Ом. Он руководствовался следующей идеей. Если над проводником, по которому проходит ток, подвесить на упругой нити магнитную стрелку, то угол поворота стрелки даст информацию о токе, об его изменениях при вариации элементов замкнутой цепи. Ом обратился к идее Кулона и построил крутильные весы. Магнитная стрелка оказалась точным и чувствительным гальванометром. В первых опытах, результаты которых Ом опубликовал в 1825 г., наблюдалась "потеря силы" (уменьшение угла отклонения стрелки) с увеличением длины проводника, подключенного к полюсам вольтова столба (поперечное сечение проводника было постоянным). Поскольку не было единиц измерения, пришлось выбрать эталон - "стандартную проволоку". В качестве зависимой переменной фигурировало уменьшение силы, действующей на магнитную стрелку. Опыты обнаружили закономерное уменьшение этой силы при увеличении длины проводника. Функция получила аналитическое выражение, но Ом не претендовал на установление закономерности, потому что гальванический элемент не давал постоянной ЭДС.
Большое внутренние сопротивление источника ЭДС, препятствовало исследованиям так, как сопротивление внешней цепи, которая использовались в опытах имела малые значения. Успех дальнейших экспериментов Ома решило открытие термоэлектричества. Ом использовал термопару висмут - медь; один спай помещался в лед, другой - в кипящую воду. Чувствительность "гальванометра" пришлось, естественно, увеличить. Процедура измерений заключалась в следующем. Восемь испытуемых проводников поочередно включались в цепь. В каждом случае фиксировалось отклонение магнитной стрелки. В следующей работе (1826 г.) Ом вводит понятие "электроскопической силы", пользуется понятием силы тока и записывает закон для участка цепи уже в форме, близкой к современной:
где X - сила тока, k - проводимость, w - поперечное сечение проводника, а - электроскопическая сила (электрическое напряжение на концах проводника), l - длина проводника. Несмотря на убедительные экспериментальные данные, проверка закона Ома продолжалась почти в течение всего XIX века.
1.2 Температурный коэффициент электрического сопротивления
Как мы уже знаем сопротивление проводников зависит от вещества, из которого они изготовлены, и их геометрических размеров
где ρ — удельное сопротивление вещества, из которого изготовлен проводник; l —длина проводника; S — площадь поперечного сечения проводника.
Сопротивление проводников входит в закон Ома для однородного участка цепи I = U / R, из которого и может быть определено R = U / I.
Из последней формулы выходит, что сопротивление проводника постоянно, поскольку, в соответствии с законом Ома, во сколько раз увеличиваем напряжение на концах проводника, во столько же раз возрастает и сила тока в нем. Все выше описанное также экспериментально было подтверждено на практических опытах
Но практике также выявилось, что можно наблюдать и другие явления. Составив электрическую цепь, схема которой показана на рис. 1. В этой цепи есть источник тока с регулированным напряжением, электрическая лампа, например автомобильная, вольтметр и амперметр, показывающие напряжение на лампе и силу тока в ней. Устанавливаем на лампе напряжение U1 и отмечаем силу тока I1. Если теперь увеличить напряжение, например в 2 раза (U2 = 2U1), то по закону Ома и сила тока должна увеличиться в 2 раза (I2 = 2I1). Однако амперметр показывает силу тока значительно меньшую, чем 2I1. Следовательно, в данном случае закон Ома не выполняется.
Рис. 1. Электрическая цепь с лампой накала
Возникло несоответствие между нашими предшествующими знаниями и новым для вас фактом — закон Ома не всегда справедлив.
Анализ дополнительной литературы и сети интернет существенно расширил наши познания в изученных закономерностях. Еще Ом в своих работах описывал об изменении проводящих свойств металлов как при нагревании так и при остывании. Нами была найдена зависимость сопротивления проводников от температуры, отличной от стандартной, которую можно выразить через следующую формулу:
Константа "альфа" (α) известна как температурный коэффициент сопротивления, который равен относительному изменению электрического сопротивления участка электрической цепи или удельного сопротивления вещества при изменении температуры на единицу. Так как все материалы обладают определенным удельным сопротивлением (при температуре 20 ° С), их сопротивление будет изменяться на определенную величину в зависимости от изменения температуры. Для чистых металлов температурный коэффициент сопротивления является положительным числом, что означает увеличение их сопротивления с ростом температуры. Для таких элементов, как углерод, кремний и германий, этот коэффициент является отрицательным числом, что означает уменьшение их сопротивления с ростом температуры. У некоторых металлических сплавов температурный коэффициент сопротивления очень близок к нулю, что означает крайне малое изменение их сопротивления при изменении температуры.
Теперь возникает вопрос почему так происходит, что с ростом температуры проводника ухудшаются его проводящие свойства. Как мы уже знаем высокая электропроводность металлов связана с тем, что в них имеется большое количество носителей тока — электронов проводимости, образующихся из валентных электронов атомов металла, которые не принадлежат определённому атому. Электрический ток в металле возникает под действием внешнего электрического поля, которое вызывает упорядоченное движение электронов. Движущиеся под действием поля электроны рассеиваются на неоднородностях ионной решётки (на примесях, дефектах решётки, а также нарушениях периодической структуры, связанной с тепловыми колебаниями ионов). При этом электроны теряют импульс, а энергия их движения преобразуются во внутреннюю энергию кристаллической решётки, что и приводит к нагреванию проводника при прохождении по нему электрического тока. Значит, теперь можем сделать вывод, что структура кристаллической решётки влияет на прохождение заряжённых частиц, а как мы уже знаем с ростом температуры происходит увеличение кинетической энергии, тем самым колебания ионных узлов решетки становятся значительными, влияя на периодичность структуры, образуя преграду для прохождения упорядоченного потока электронов, и этим увеличивая сопротивление проводника.
Полупроводники в свою очередь при низких температурах наоборот страдают недостатком носителей электрических зарядов. По этому при их нагревании количество носителей возрастает, что приводит к снижению сопротивления. Если иметь в виду, что размеры металлов при нагревании изменяются мало, то соответствующую формулу можно записать и для удельного сопротивления металлических проводников
Тщательные исследования показывают, что сопротивление металлических проводников зависит от их температуры практически линейно и график такой зависимости представлен на рис. 2.
Рис 2. График зависимости сопротивления металлического проводника от температуры.
2. Исследования проводников
Одним из возможных способов изучения и демонстрации зависимости электрического сопротивления проводника от температуры может служить лабораторная установка. Такая установка была реализована по схеме (рис. 1.) и в ее состав вошли:
1) регулируемый низковольтный источник напряжения
2) автомобильная лампа накаливания на 12 вольт
3) в качестве вольтметра использовался цифровой мультиметр VC 9808
4) роль амперметра выполнил цифровой мультиметр DT -832

В ходе эксперимента была составлена вольт- амперная характеристика (таблица 1) , которая потвердела выше изложенные доводы.
Что такое электрическое сопротивление и как оно зависит от температуры

Любой элемент или участок электрической цепи с точки зрения электромагнитного процесса, происходящего в нем прежде всего характеризуется способностью проводить ток или препятствовать прохождению тока. Это свойство элементов цепи оценивается их электрической проводимостью или величиной, обратной проводимости — электрическим сопротивлением.
Большинство электротехнических устройств состоит из токопроводящих частей, выполненных из металлических проводников, снабженных обычно изоляционным покрытием или оболочкой. Электрическое сопротивление проводника зависит от его геометрических размеров и свойств материала. Величина электрического сопротивления равна:
где l — длина проводника, м; s — площадь поперечного сечения проводника, мм2; ρ — удельное сопротивление проводника, ом·мм2/м; γ — удельная проводимость, м/ом·мм.
Удельное электрическое сопротивление
Удельное сопротивление и удельная проводимость учитывают свойства материала проводника и дают значения сопротивления и проводимости проводника длиной 1 м и площадью поперечного сечения 1 мм2.
По величине удельного сопротивления ρ все материалы можно разделить на три группы:
- проводники — металлы и их сплавы (ρ от 0,015 до 1,2 ом·мм2/м);
- электролиты и полупроводники (ρ от 102 до 206 ом·мм2/м);
- диэлектрики, или изоляторы (ρ от 1010 до 2011 ом·мм2/м).
Другие устройства, наоборот, должны иметь значительные сопротивления (электрические лампы накаливания, нагрева тельные приборы и т. д.), поэтому их токоведущие элементы следует выполнять из материалов с большим удельным сопротивлением ρ, обычно представляющих собой сплавы металлов. К ним относятся, например, манганин, константан, нихром, которые имеют значения ρ от 0,1 до 1,2.

Зависимость электрического сопротивления от температуры
Величина электрического сопротивления зависит также от температуры проводника, которая может изменяться вследствие нагревания проводника электрическим током или вследствие изменения температуры внешней среды. При изменении температуры проводника изменяется величина его удельного сопротивления. Приведенные выше значения р для некоторых материалов справедливы при температуре.
Независимость сопротивления от температуры приближенно выражается так:
Rto — сопротивление проводника при температуре to, R20о— то же при температуре 20°С, ом; α — температурный коэффициент электрического сопротивления, показывающий относительное изменение сопротивления проводин ка при нагревании его на 1°С.
Из этого выражения величина α равна:
α = (Rto - R20о)/(R20о·(to-20°)).
Для большинства металлов и их сплавов величина α > 0, т. е. при нагревании сопротивление их увеличивается и наоборот.
Для проводков из чистых металлов значения, а колеблются в пределах от 0,0037 до 0,0065 на 1°С. Для сплавов высокого сопротивления α имеет весьма малые значения, в десятки и сотни раз меньшие, чем у проводников из чистых металлов. Так, например, для манганина α = 0,000015 на °С.
Значения α для полупроводников электролитов отрицательны, порядка 0,02. Температурный коэффициент электрического сопротивления также отрицателен и по своему абсолютному значению в десятки раз превышает α для металлов.
Зависимость сопротивления от температуры широко используется в технике для измерения температур при помощи так называемых термометров сопротивления, у которых α должен быть большим. В ряде приборов, наоборот, применяются материалы с малым значением α для того, чтобы исключить влияние колебаний температуры на показания этих приборов.
Сопротивление переменного тока
Сопротивление одного и того же проводника для переменного тока будет больше, чем для постоянного. Это объясняется явлением так называемого поверхностного эффекта, заключающегося в том, что переменный ток вытесняется от центральной части проводника к периферийным слоям. В результате плотность тока во внутренних слоях будет меньше, чем в наружных.
Таким образом, при переменном токе сечение проводника используется как бы неполностью. Однако при частоте 50 гц различие в сопротивлениях постоянному и переменному токам незначительно и практически им можно пренебречь.

Сопротивление проводника постоянному току называют омическим, а переменному току — активным сопротивлением. Омическое и активное сопротивления зависят от материала (внутренней структуры), геометрических размеров и температуры проводника. Кроме того, в катушках со стальным сердечником на величину активного сопротивления влияют потери в стали.К активным сопротивлениям относят электрические лампы накаливания, электрические печи сопротивления, различные нагревательные приборы, реостаты и провода, где электрическая энергия практически почти целиком превращается в тепловую.
Кроме активного сопротивления в цепях переменного тока есть индуктивное и емкостное сопротивления.
Сопротивление изоляции
Надежность работы электрической сети и аппаратуры в значительной степени зависит от качества изоляции между токоведущими частями различных фаз, а также между токоведущими частями и землей.
Качество изоляции характеризуется величиной ее сопротивления. Определением этой величины обычно ограничиваются при контрольных испытаниях сетей и установок с напряжением меньше 1000 В. Для установок более высокого напряжения дополнительно определяются электрическая прочность и диэлектрические потери.
В зависимости от состояния сети (сеть с выключенными или включенными приемниками энергии, находящаяся или не находящаяся под напряжением) применяют различные схемы включения измерительных приборов и способы подсчета величины сопротивления изоляции. Наиболее широко для этой цели используются мегаомметры и вольтметры.
Для чего нужен расчет проводов на нагрев
Электрическое сопротивление влияет на нагрев проводов и кабелей. Провода, соединяющие источник энергии с приемниками, должны обеспечить питание приемников с малой потерей напряжения и энергии, но при этом они не должны нагреваться проходящим по ним током выше допустимой температуры.
Превышение допустимых значений температуры приводит к повреждению изоляции проводов и, как следствие этого, к короткому замыканию, т. е. резкому повышению величины тока в цепи. Поэтому расчет проводов позволяет определить площадь их поперечного сечения, при которой потеря напряжения и нагревание проводов будут в пределах нормы.
Обычно сечение проводов и кабелей на нагрев проверяется по таблицам допустимых токовых нагрузок из ПУЭ. Если сечение не подходит по условиям нагрева, следует выбрать большее сечение, которое удовлетворяет этим требованиям.
Установки нагрева сопротивлением
Основными элементами электропечей являются электрические нагревательные элементы и теплоизоляционное устройство, предотвращающее потери тепла в окружающее пространство. В качестве материала для электрических нагревательных элементов используются жароупорные неметаллические материалы с высоким удельным сопротивлением (уголь, графит, карборунд) и металлические материалы (нихром, константан, фехраль и т. п.).
Применение материалов с высоким удельным сопротивлением ρ позволяет конструировать нагревательные элементы с большой площадью поперечного сечения и поверхности, а выбор материалов, обладающих небольшим коэффициентом расширения α, обеспечивает неизменяемость геометрических размеров элемента при нагреве.
Нагревательные элементы из материалов типа графита изготавливаются в виде стержней с трубчатым или сплошным сечением. Металлические нагревательные элементы изготовляются в виде проволоки или ленты.
Использование плавких предохранителей
Для защиты проводов электрической цепи от токов, превышающих допустимые значения, применяются автоматические выключатели и плавкие предохранители различных типов. В принципе плавкий предохранитель представляет собой участок электрической цепи с малой термической устойчивостью.
Зависимость электрического сопротивления от температуры
При проектировании электрических схем, инженеры сталкиваются с тем, что проводники обладают определенным сопротивлением, на которое оказывают влияния температурные колебания. Статья даст подробное описание, что такое зависимость сопротивления от температуры и как температура влияет на проводимость различных веществ — металлов, газов и жидкостей. Дополнительно будет приведена формула расчета такой зависимости.

Сопротивление
Сопротивлением называется способность проводника пропускать через себя электрический ток. Единицей измерения данной физической величины является Ом. На принципиальных схемах эта величина обозначается буквой «R». На величину сопротивления любого проводника электрическому току влияет его структура. Двигаясь внутри структуры, свободные электроны сталкиваются с атомами и электронами, которые замедляют их движение. Чем их концентрация больше, тем выше будет само электрическое сопротивление.

О способности проводников проводит электрический ток судят по величине его удельного сопротивления. Удельное сопротивление проводника — это сопротивление протеканию тока через проводник из любого вещества с площадью поперечного сечения 1 м² и длиной один метр. Обозначается в физике данная величина буквой «ρ». Данный параметр является табличной величиной и измеряется в системе СИ как Ом×м (может также измеряться в Ом×см и Ом×мм²/м).

Коэффициент сопротивления
Во время работы электрических цепей прослеживается прямая зависимость сопротивления металлов от температуры. Это явление называют коэффициентом температурного сопротивления. Оно определяет соотношение сопротивления к температурным изменениям. Объясняется это явление следующим образом: с повышением температуры структура проводника получает долю тепловой энергии, вследствие чего эта энергия увеличивает скорость движения атомов. В результате повышается вероятность их столкновения со свободными электронами. Чем чаще происходят эти столкновения, тем ниже будет проводимость.
Можно провести простой опыт: в электрическую схему из аккумулятора и омметра подключим кусок медной проволоки. При таком подключении схема будет иметь строго определенное значение сопротивления. Далее надо будет нагреть медную проволоку. В момент нагрева можно заметить, что сопротивление всей схемы растет, а после остывания проводника оно наоборот уменьшается. На основании такого опыта довольно просто прослеживается температурная зависимость сопротивления проводника.

Температурный коэффициент отображает увеличение сопротивления при изменении температуры вещества на 1 градус. Для максимально чистого металла это значение равняется 0.004 °С -1 . То есть, при увеличении температуры на 10 градусов, электрическая проводимость в металлах изменится на 4 % в большую сторону. Данная величина обозначается буквой «α». При расчете сопротивления через удельное сопротивление используется такая формула:

В данной зависимости:
- «R» — сопротивление, Ом;
- «l» — длина проводника, м;
- «s» — поперечное сечение проводника, м²;
- «ρ» — значение удельного сопротивления, Ом×м.
Зависимость проводимости металлического проводника от температуры можно проследить с помощью таких выражений:

Для металлов все предельно просто — изменение температуры приводит к увеличению его сопротивления. Ниже будет дано описание этой зависимости для газов, которые по своей природе являются диэлектриками.
Для закрепления материала, решим следующую задачу:
Имеется стальной проводник, диаметр которого равен один миллиметр, а длина его составляет 100 метров. Определите сопротивление такого проводника из стали, если величина удельного сопротивления стального проводника составляет 12×10 -8 Ом×м.
Определяем сопротивление проводника по формуле:
где S является площадью поперечного сечения. Определить площадь можно с помощью формулы:
S= π×r 2 = π×d 2 /2 2 =3.14×(1×10 -3 ) 2 /4=3.14×10 -6 /4=0.785×10 -6 м 2
После этого можно определить сопротивление:
R=12×10 -8 ×100/(0.785×10 -6 )=15.287 Ом
Газы не являются проводниками, но их проводимость так же зависит от температуры. Происходит это за счет так называемого эффекта ионизации. Ионизация в газах происходит за счет насыщения их жидкостью или иными веществами, которые способны проводить электрический ток. Проследить то, как увеличивается сопротивление при повышении температуры газа можно на таком опыте.

К схеме с амперметром и аккумулятором добавим 2 металлические пластины, которые не соприкасаются друг с другом. Такая электрическая цепь является разомкнутой. Между пластинами поместим зажженную горелку. При нагреве происходит смещение стрелки амперметра в сторону увеличения. То есть такую цепь можно считать замкнутой. На основании этого можно сделать вывод, что с ростом температуры воздух ионизируется, происходит снижение его сопротивления и увеличение проводимости заряженных электронов. Данный эффект называют пробоем изоляционного слоя газа, зависящий от степени их ионизации и величины протекающего напряжения. Подобное явление знакомо каждому из нас — это грозовой разряд.
Жидкости
В жидкостях прослеживается обратная зависимость. С увеличением температуры, сопротивление жидкого проводника уменьшается. Для электролита свойственно правило отрицательного значения температурного коэффициента — а˂0. Удельное сопротивление электролита рассчитывается следующим образом:
При этом увеличившееся значение температуры электролита сопровождается уменьшением сопротивления и ростом его проводимости.
Сверхпроводимость
Снижение температуры металлических проводников сильно увеличивает их проводимость. Это связано с тем, что в структуре вещества замедляется движение атомов и электронов, благодаря чему снижается вероятность их столкновения со свободными электронами. При температуре абсолютного 0 (–273 градуса Цельсия) возникает явление падения до нуля сопротивления проводника. Зависимость сопротивления проводника от температуры при абсолютном 0 — сверхпроводимость.
Температура, при которой обычный проводник становится сверхпроводником, называется критической. Она будет разной для различных чистых металлов и сплавов. Все будет зависеть от их структуры, химического состава и структуры кристаллов. Например, серое олово с алмазной структурой является полупроводником. Но белое олово при своей тетрагональной кристаллической ячейке, мягкости и плавкости, переходит в состояние сверхпроводника при температуре 3.70 К. Также при критической температуре прослеживается целый ряд других способностей:
- Повышение частоты переменного тока вызывает рост сопротивления, значение гармоник с периодом световой волны.
- Способность удерживать величину силы тока ранее приложенного, а затем отключенного источника.

Металл или сплав может перейти в состояние сверхпроводника и при нагревании. Такое явление называют высокотемпературной проводимостью. Ответ на вопрос, почему от высокой температуры сопротивление металлов снижается, может довольно просто объяснить их кристаллическая структура. В момент нагрева до критических значений, электроны перестают хаотично перемещаться внутри структуры вещества. Они выстраиваются в цепочку. Такое построение не мешает движению свободных электронов, а значит падает общее сопротивление. Переход в состояние высокотемпературной проводимости начинается с порога 1000К и этот показатель выше, чем точка кипения азота.
Применение
Свойство проводников изменять сопротивление при определённой температуре используют для создания различных элементов электрических схем и измерительных приборов. О них будет рассказано далее в данной статье.
Резистор
Сопротивление устройств старого типа сильно зависело от их нагрева. При нагревании проводимость резистора пропорционально изменялась в меньшую сторону. Для электрических цепей требуется идеальный резистор, который обладает наивысшим коэффициентом проводимости. Для снижения нагрева при производстве данных устройств теперь используется материал, имеющий малую зависимость сопротивления от температуры нагрева. Это позволило применять резисторы с малым сопротивлением для цепей с большим напряжением.

Терморезистор
Существует отдельная группа резисторов, которые применяют для измерения температуры. Особенностью такого устройства является то, что он может снижать свою проводимость при нагреве. При этом он отключает цепь при достижении определенного порогового значения.

Термометр сопротивления
Это прибор был разработан для измерения температуры среды. Он состоит из тонкой платиновой проволоки, защитного чехла и корпуса. Прибор имеет стабильную реакцию на перепады температуры. Измеряемой величиной в данном устройстве служит сопротивление этой проволоки из платины. Чем выше будет температура, тем сопротивление соответственно будет больше. Понижение сопротивления так же фиксируется, так как в этот момент меняются проводимость и сопротивление. Для измерения температуры термометром сопротивления, в настоящее время применяются проволочные индикаторы из разнообразных металлов. В зависимости от свойств используемого металла, погрешность устройства может составлять не более 0.1 %. Благодаря этому достигается очень высокая точность измерения температуры.

Самый известный нам газовый проводник — это люминесцентная лампа. Газ нагревается за счет увеличения напряжения между анодом и катодом лампы.

Известным жидкостным проводником является щелочной аккумулятор. При понижении температуры нарушается структура жидкости и изменяется ее сопротивление.

Нагрев провоцирует движение атомов и электронов, увеличивая сопротивление и зарядный ток устройства.
Заключение
В данной статье мы рассмотрели, как зависит сопротивление от температуры. Металлы, газы и жидкости имеют свойства изменять свою проводимость и сопротивление при температурных перепадах. Это свойство изменения электрического сопротивления используются для измерения температуры среды. Наибольшая точность измерений температуры в настоящее время достигается за счет применения современных материалов, даже в бытовой технике.
Урок 32. Электрический ток в металлах
Свободные электроны – это электроны, не связанные с определенными атомами.
Сверхпроводимость – физическое явление, заключающееся в скачкообразном падении до нуля сопротивления вещества.
Температурный коэффициент сопротивления - величина, равная относительному изменению электрического сопротивления участка электрической цепи или удельного сопротивления вещества при изменении температуры на 1 К.
Основная и дополнительная литература по теме урока:
Мякишев Г. Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 216-224.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. - М.: Дрофа, 2009.- С.81-89.
М.М. Балашов О природе М., Просвещение, 1991г.
Е.А. Марон, А.Е. Марон Сборник качественных задач по физике. М., Просвещение, 2006
Я.И. Перельман Занимательная физика. М.: “Наука”, 1991.
Основное содержание урока
Все тела по проводимости электрического тока делятся на проводники, полупроводники и диэлектрики. Для того чтобы электрическую энергию доставить от источника тока потребителю составляют электрические цепи. В большинстве случаев в электрической цепи используются металлические провода. По физической природе зарядов – носителей электрического тока, электропроводность подразделяют на:
Какие заряженные частицы движутся в металлах при наличии тока?
После открытия в 1897 году английским ученым Дж. Дж. Томсоном электрона стали разрабатываться теории, объясняющие электропроводность металлов. Автором первой теории был Пауль Друде – немецкий физик. Эта теория нуждалась в опытном обосновании. В 1901 г. немецкий физик Э. Рикке поставил опыт по исследованию прохождения тока в металлах.
Результаты опыта свидетельствовали о том, что в переносе заряда в металлах ионы не участвуют. Впоследствии вопросом проводимости металлов заинтересовались и другие учёные. В 1913 году российские учёные Л. И. Мандельштам и Н. Д. Папалекси провели опыты по исследованию проводимости металлов. Суть опытов сводилась к тому, что катушка, на которую наматывали металлическую проволоку приводили во вращательное движение и резко тормозили. При торможении электроны продолжали двигаться по инерции и гальванометр, соединенный с катушкой фиксировал появление тока. По направлению отклонения стрелки гальванометра было установлено, что ток создается движением отрицательно заряженных частиц. На основании измерения отношения заряда частиц к их массе выяснилось, что ток создается движением свободных электронов. Аналогичный опыт был поставлен в 1916 году американскими учеными Т. Стюартом и Р. Толменом. Результаты опытов говорили, что ток в металлах создается движением электронов.

После анализа имеющихся данных о прохождении тока в металлах разными учеными была разработана современная классическая теория проводимости тока металлами. Основные положения электронной теории проводимости металлов.
1. Металл можно описать следующей моделью: кристаллическая решетка ионов погружена в идеальный электронный газ, состоящий из свободных электронов. У большинства металлов каждый атом ионизирован, поэтому концентрация свободных электронов приблизительно равна концентрации атомов 1023- 1029м-3 и почти не зависит от температуры.
2.Свободные электроны в металлах находятся в непрерывном хаотическом движении.
3. Электрический ток в металле образуется только за счет упорядоченного движения свободных электронов.
Опираясь на данную теорию удалось объяснить основные законы электрического тока в металлах. Исходя из электронной теории можно найти связь между силой тока в металлах и скоростью движения электронов.
Сила тока равна произведению заряда электрона, их концентрации, площади сечения проводника и средней скорости движения электронов:
ОтсюдаЕсли в эту формулу подставлять числовые данные силы тока, концентрации и площади сечения для разных металлов, то мы увидим, что средняя скорость движения электронов составляет всего лишь какие-то доли миллиметра в секунду. Когда говорят о скорости распространения тока имеют в виду скорость распространения электрического поля в проводнике, которое равно скорости света.
На силу тока в проводнике влияет и сопротивление проводника. Опыт показывает, что сопротивление металлов зависит от температуры. Увеличение сопротивления можно объяснить тем, при повышении температуры увеличивается скорость и амплитуда хаотического движения ионов кристаллической решетки металла и свободных электронов. Это приводит к более частым их соударениям, что затрудняет направленное движение электронов, то есть увеличивает электрическое сопротивление.
зависимость сопротивления металлов от температуры выражается формулой:
При нагревании размеры проводника практически не меняются, в основном меняется удельное сопротивление. Учет зависимости сопротивления от температуры используется в термометрах сопротивления.
Формула зависимости удельного сопротивления металлического проводника от температуры имеет вид:
где ρ0 - удельное сопротивление при 0 градусов,
α - температурный коэффициент сопротивления.
Графиком зависимости ⍴(t) является прямая.

Хотя коэффициент α довольно мал, учет зависимости сопротивления от температуры при расчете нагревательных приборов совершенно необходим.
При понижении температуры сопротивление металлов должно уменьшаться. В 1911 году датский физик Х. Каммерлинг - Оннес открыл явление, названное сверхпроводимостью. Исследуя зависимость сопротивления ртути от температуры, он обнаружил, что при температуре 4,12 К сопротивление ртути исчезает. В сверхпроводящее состояние могут перейти многие химические соединения и сплавы. Некоторые вещества, переходящие при низких температурах в сверхпроводящее состояние, не являются проводниками при обычных температурах.
Вещества, находящиеся в сверхпроводящем состоянии, приобретают новые свойства. Наиболее важным из них является способность длительное время (многие годы) поддерживать без затухания электрический ток в проводниках.
Классическая электронная теория не способна объяснить явление сверхпроводимости. Теоретическое объяснение явления сверхпроводимости на основе квантово-механических представлений было дано учеными Дж. Бардиным, Дж. Шриффером (США) и Н. Н. Боголюбовым (СССР) в 1957 г.
В 1986 году была обнаружена высокотемпературная сверхпроводимость (при 100 К).
В настоящее время ведутся интенсивные работы по поиску новых веществ переходящими в сверхпроводящее состояние при более высокой температуре. Ученые надеются получить вещество в сверхпроводящем состоянии при комнатной температуре. Если удастся создать сверхпроводник при нормальной температуре, то будет решена проблема передачи электроэнергии по проводам без потерь.
Следует отметить, что до настоящего времени механизм высокотемпературной сверхпроводимости керамических материалов до конца не выяснен.
Открытие вещества, переходящего в сверхпроводящее состояние при комнатной температуре, позволило бы упростить решение многих технических вопросов. Во-первых, отсутствие сопротивления означает отсутствие каких-либо потерь на нагревание. Отсутствие нагревания и потерь энергии на него чрезвычайно важно для электродвигателей и электронной вычислительной техники, а также для передачи электроэнергии.
В сверхпроводниках из-за отсутствия сопротивления протекают чрезвычайно высокие токи, создающие сильные магнитные поля, что может применяться при термоядерном синтезе для удержания высокотемпературной плазмы в реакторе.
На сегодняшний момент в некоторых странах существует железнодорожная сеть с поездами на магнитной подушке. После открытия сверхпроводимости Камерлинг-Оннес, пытаясь создать сверхпроводящий электромагнит, обнаружил, что изменение тока, или же магнитные поля, разрушают эффект сверхпроводимости. Только к середине двадцатого века удалось создать сверхпроводящие электромагниты. На данный момент продолжаются исследования по изучению высокотемпературной сверхпроводимости.
Разбор типовых тренировочных заданий
1. Сопротивление железного проводника при 0 0 С и 600 0 С равны соответственно 2 Ом и 10 Ом. Каков температурный коэффициент железа?
Зависимость сопротивления металлов от температуры определяется формулой
Из этой формулы выразим температурный коэффициент железа – α
После подстановки числовых данных получаем
2. Какова скорость дрейфа электронов в медном проводе диаметром 5 мм, по которому к стартеру грузовика подводится ток 100 А. Молярная масса медиСила тока в проводнике равна:
Выразим скорость из этой формулы:
Концентрацию электронов найдем по формуле:
Число электронов найдём по формуле:
Площадь сечения равна:
Учитывая всё это запишем конечную формулу для расчёта скорости дрейфа электронов:
Читайте также:
