Все металлы имеют положительный заряд
В этом листке мы приступаем к подробному изучению того, как осуществляется прохождение электрического тока в различных проводящих средах — твёрдых телах, жидкостях и газах.
Напомним, что необходимым условием возникновения тока является наличие в среде достаточно большого количества свободных зарядов, которые могут начать упорядоченное движение под действием электрического поля. Такие среды как раз и называются проводниками электрического тока.
Наиболее широко распространены металлические проводники. Поэтому начинаем мы с вопросов распространения электрического тока в металлах.
Мы много раз говорили о свободных электронах, которые являются носителями свободных зарядов в металлах. Вам хорошо известно, что электрический ток в металлическом проводнике образуется в результате направленного движения свободных электронов.
Свободные электроны
Металлы в твёрдом состоянии имеют кристаллическую структуру: расположение атомов в пространстве характеризуется периодической повторяемостью и образует геометрически правильный рисунок, называемый кристаллической решёткой.
Атомы металлов имеют небольшое число валентных электронов, расположенных на внешней электронной оболочке. Эти валентные электроны слабо связаны с ядром, и атом легко может их потерять.
Когда атомы металла занимают места в кристаллической решётке, валентные электроны покидают свои оболочки — они становятся свободными и отправляются «гулять» по всему кристаллу (а именно, свободные электроны перемещаются по внешним орбиталям соседних атомов. Эти орбитали перекрываются друг с другом вследствие близкого расположения атомов в кристаллической решётке, так что свободные электроны оказываются «общей собственностью» всего кристалла). В узлах кристаллической решётки металла остаются положительные ионы, пространство между которыми заполнено «газом» свободных электронов (рис. 1 ).
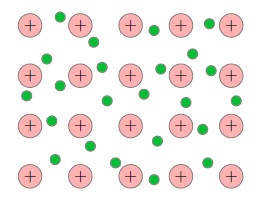
Рис. 1. Свободные электроны
Свободные электроны и впрямь ведут себя подобно частицам газа (другой адекватный образ — электронное море, которое «омывает» кристаллическую решётку) — совершая тепловое движение, они хаотически снуют туда-сюда между ионами кристаллической решётки. Суммарный заряд свободных электронов равен по модулю и противоположен по знаку общему заряду положительных ионов, поэтому металлический проводник в целом оказывается электрически нейтральным.
Газ свободных электронов является «клеем», на котором держится вся кристаллическая структура проводника. Ведь положительные ионы отталкиваются друг от друга, так что кристаллическая решётка, распираемая изнутри мощными кулоновскими силами, могла бы разлететься в разные стороны. Однако в тоже самое время ионы металла притягиваются к обволакивающему их электронному газу и, как ни в чём не бывало, остаются на своих местах, совершая лишь тепловые колебания в узлах кристаллической решётки вблизи положений равновесия.
Что произойдёт, если металлический проводник включить в замкнутую цепь, содержащую источник тока? Свободные электроны продолжают совершать хаотическое тепловое движение, но теперь — под действием возникшего внешнего электрического поля — они вдобавок начнут перемещаться упорядоченно. Это направленное течение электронного газа, накладывающееся на тепловое движение электронов, и есть электрический ток в металле (поэтому свободные электроны называются также электронами проводимости). Скорость упорядоченного движения электронов в металлическом проводнике, как нам уже известно, составляет приблизительно 0,1мм/с.
Опыт Рикке
Почему мы решили, что ток в металлах создаётся движением именно свободных электронов? Положительные ионы кристаллической решётки также испытывают на себе действие внешнего электрического поля. Может, они тоже перемещаются внутри металлического проводника и участвуют в создании тока?
Упорядоченное движение ионов означало бы постепенный перенос вещества вдоль направления электрического тока. Поэтому надо просто пропускать ток по проводнику на протяжении весьма длительного времени и посмотреть, что в итоге получится. Такого рода эксперимент и был поставлен Э.Рикке в 1901 году.
В электрическую цепь были включены три прижатых друг к другу цилиндра: два медных по краям и один алюминиевый между ними (рис. 2 ). По этой цепи пропускался электрический ток в течение года.
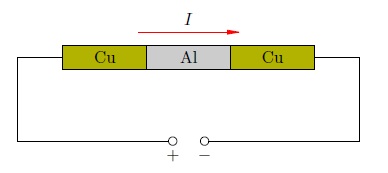
Рис. 2. Опыт Рикке
За год сквозь цилиндры прошёл заряд более трёх миллионов кулон. Предположим, что каждый атом металла теряет по одному валентному электрону, так что заряд иона равен элементарному заряду Кл. Если ток создаётся движением положительных ионов, то нетрудно подсчитать (сделайте это сами!), что такая величина прошедшего по цепи заряда соответствует переносу вдоль цепи около 2кг меди.
Однако после разъединения цилиндров было обнаружено лишь незначительное проникновение металлов друг в друга, обусловленное естественной диффузией их атомов (и не более того). Электрический ток в металлах не сопровождается переносом вещества, поэтому положительные ионы металла не принимают участия в создании тока.
Опыт Стюарта–Толмена
Прямое экспериментальное доказательство того, что электрический ток в металлах создаётся движением свободных электронов, было дано в опыте Т.Стюарта и Р.Толмена (1916 год).
Эксперименту Стюарта–Толмена предшествовали качественные наблюдения, сделанные четырьмя годами ранее русскими физиками Л.И.Мандельштамом и Н.Д.Папалекси. Они обратили внимание на так называемый электроинерционный эффект: если резко затормозить движущийся проводник, то в нём возникает кратковременный импульс тока. Эффект объясняется тем, что в течение небольшого времени после торможения проводника его свободные заряды продолжают двигаться по инерции.
Однако никаких количественных результатов Мандельштам и Папалекси не получили, и наблюдения их опубликованы не были. Честь назвать опыт своим именем принадлежит Стюарту и Толмену, которые не только наблюдали указанный электроинерционный эффект, но и произвели необходимые измерения и расчёты.
Установка Стюарта и Толмена показана на рис. 3 .
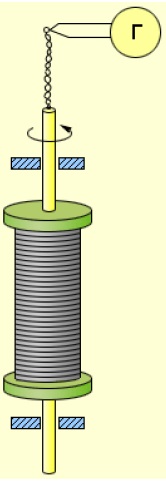
Рис. 3. Опыт Стюарта–Толмена
Катушка большим числом витков металлического провода приводилась в быстрое вращение вокруг своей оси. Концы обмотки с помощью скользящих контактов были подсоединены к специальному прибору — баллистическому гальванометру, который позволяет измерять проходящий через него заряд.
После резкого торможения катушки в цепи возникал импульс тока. Направление тока указывало на то, что он вызван движением отрицательных зарядов. Измеряя баллистическим гальванометром суммарный заряд, проходящий по цепи, Стюарт и Толмен вычислили отношение заряда одной частицы к её массе. Оно оказалось равно отношению для электрона, которое в то время уже было хорошо известно.
Так было окончательно выяснено, что носителями свободных зарядов в металлах являются свободные электроны. Как видите, этот давно и хорошо знакомый вам факт был установлен сравнительно поздно — учитывая, что металлические проводники к тому моменту уже более столетия активно использовались в самых разнообразных экcпериментах по электромагнетизму (сравните, например, с датой открытия закона Ома — 1826 год. Дело, однако, заключается в том, что сам электрон был открыт лишь в 1897 году).
Зависимость сопротивления от температуры
Опыт показывает, что при нагревании металлического проводника его сопротивление увеличивается. Как это объяснить?
Причина проста: с повышением температуры тепловые колебания ионов кристаллической решётки становятся более интенсивными, так что число соударений свободных электронов с ионами возрастает. Чем активнее тепловое движение решётки, тем труднее электронам пробираться сквозь промежутки между ионами (Представьте себе вращающуюся проходную дверь. В каком случае труднее проскочить через неё: когда она вращается медленно или быстро? :-)). Скорость упорядоченного движения электронов уменьшается, поэтому уменьшается и сила тока (при неизменном напряжении). Это и означает увеличение сопротивления.
Как опять-таки показывает опыт, зависимость сопротивления металлического проводника от температуры с хорошей точностью является линейной:
Здесь — сопротивление проводника при . График зависимости (1) является прямой линией (рис. 4 ).
Множитель называется температурным коэффициентом сопротивления. Его значения для различных металлов и сплавов можно найти в таблицах.
Длина проводника и его площадь поперечного сечения при изменении температуры меняются несущественно. Выразим и через удельное сопротивление:
и подставим эти формулы в (1) . Получим аналогичную зависимость удельного сопротивления от температуры:
Коэффициент весьма мал (для меди, например, ), так что температурной зависимостью сопротивления металла часто можно пренебречь. Однако в ряде случаев считаться с ней приходиться. Например, вольфрамовая спираль электрической лампочки раскаляется до такой степени, что её вольт-амперная характеристика оказывается существенно нелинейной.
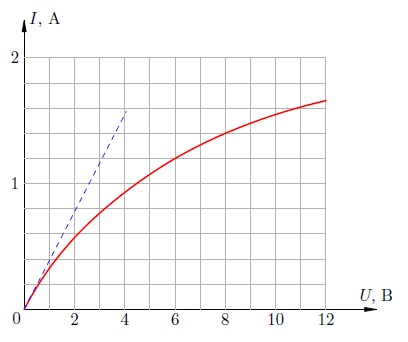
Рис. 5. Вольт-амперная характеристика лампочки
Так, на рис. 5 приведена вольт-амперная характеристика автомобильной лампочки. Если бы лампочка представляла собой идеальный резистор, её вольт-амперная характеристика была прямой линией в соответствии с законом Ома. Эта прямая изображена синим пунктиром.
Однако по мере роста напряжения, приложенного к лампочке, график отклоняется от этой прямой всё сильнее и сильнее. Почему? Дело в том, что с увеличением напряжения ток через лампочку возрастает и больше разогревает спираль; сопротивление спирали поэтому также увеличивается. Следовательно, сила тока хотя и продолжит возрастать, но будет иметь всё меньшее и меньшее значение по сравнению с тем, которое предписывается «пунктирной» линейной зависимостью тока от напряжения.
Виды металлических связей и как они образуются
Все вещества во Вселенной имеют свою структуру строения, а следовательно — и свои свойства. Об особой связи частиц веществ впервые написал Уильям Хиггинс в XVIII веке. Тогда в своем научном труде ученый описал «особую соединительную силу», которая стала основой для возникновения теории о валентности, а позже — теории о химических связях.
Современная химия описывает существование нескольких типов химических связей:
- металлическая;
- ковалентная;
- ионная;
- водородная;
- ван-дер-ваальсова.
Атомы металлов между собой объединяются в вещества с появлением новых свойств. При этом связь между атомами-металлами отличается свойствами от ковалентной и ионной связей.
Металлическая связь — особый вид химической связи, возникающий между атомами металлов за счет обобществления их крайних электронных оболочек и валентных электронов. Металлическая связь встречается в простых веществах металлах и их сплавах.
Металлическая связь формируется за счет частиц двух видов:
- ионизированных атомов металлов, которые в процессе формирования отдают электроны, а значит получают положительный заряд;
- свободных электронов, называемых «электронным газом», имеющих отрицательный заряд по своей природе происхождения.
Вещества с металлической связью чаще всего представляют собой чистые соединения и сплавы различных металлов, которые образуют новые вещества, например, бронзу, сталь, чугун, латунь и другие.
Атомы металлов имеют ряд особенностей:
- небольшое количество электронов на внешнем электронном уровне;
- большие радиусы.
Благодаря данным характеристикам соединения металлов легко отдают внешние электроны, что позволяет им становиться ионами с положительным зарядом.
По природе происхождения металлическая связь близка к ковалентной, а также к ионным соединениям, но в силу ряда отличий представляет собой отдельный тип химических связей.
Сходства и отличия металлической химической связи от ионной и ковалентной
Все виды связи переплетаются между собой и имеют сходные черты. Более того, некоторые соединения могут иметь сразу несколько видов связи в одной молекуле.
Металлическая связь сходна с ионной тем, что атомы металлов в соединениях легко отдают свои валентные электроны, которые слабо связаны со своими атомными ядрами. Отрыв электронов от ядра приводит к формированию катионов металлов.
Обобществление отрицательно заряженных электронов по системе частично перекрывающихся орбиталей металлов приводит к формированию прочной химической связи, что напоминает по механизму образования ковалентную связь.
Каждый из видов связи имеет свои особенности построения решеток, взаимодействия частиц, а также характерные свойства.
Несмотря на схожесть металлической связи с ковалентной и ионной, каждая из них имеет ряд характерных черт, благодаря которым можно легко определить вид связи в соединении.
Металлическая связь в отличие от ковалентной имеет высокую концентрацию электронов проводимости в атомах металлов. Она менее прочна, чем ковалентная, а ее энергия связей меньше в 3-4 раза.
В отличие от ковалентной связи металлическая:
- ненасыщаема— объединяет большое количество атомов;
- ненаправлена и делокализирована и электроны в связи обобществляются всеми атомами соединения.
В отличие от ионной связи металлическая образуется между катионами и отрицательно заряженными электронами, которые не привязаны к одному атомному ядру, а свободно движутся по кристаллической решетке.
Виды, особенности образования, как происходит, схема
Металлическая связь не может существовать между отдельными соединенными между собой атомами. Она появляется только в веществах.
При этом связи в этих веществах не отличаются постоянством. Электроны, отделившиеся от атомов металлов, превращаются в «электронный газ», благодаря чему они могут спокойно путешествовать по кристаллической решетке.
Основой для образования металлической химической связи является наличие свободных атомных орбиталей, а также свободных электронов.
Схему образования металлической связи можно записать следующим образом:
Число n будет зависеть от места химического элемента в Периодической системе химических элементов Д. И. Менделеева. Число внешних электронов равно номеру группы, в которой находится металл.
Характерные кристаллические решетки
Кристаллическая решетка в веществах с металлической связью является основой, неким каркасом кристалла, в узлах которой находятся ионы металла, а между ними в виде «электронного газа» перемещаются отрицательно заряженные электроны, периодически присоединяющиеся к ионам металлов, превращая их в атомы.
Форма кристаллической решетки отличается в зависимости от группы, к которой относится металл:
- щелочные металлы (литий Li, калий K, рубидий Rb и другие) имеют объемно-центрированную кубическую кристаллическую решетку;
- переходные элементы (алюминий Al, медь Cu, цинк Zn и другие) имеют гранецентрированную кубическую форму решетки;
- щелочноземельные металлы (бериллий Be, кальций Ca, радий Ra, кроме бария) имеют гексагональную решетку;
- индий In имеет тетрагональную решетку;
- ртуть Hg имеет ромбоэдрическую решетку.
Физические свойства металлов
Почти все металлы и их сплавы имеют сходные физические свойства:
Условия существования электрического тока в металлах
Электрический ток в металлах — это упорядоченное (направленное) движение электронов под действием электрического поля.
Особенность металлических проводников состоит в том, что заряд электричества переносят свободные электроны. Они перемещаются в одном направлении под влиянием внешнего электрического поля, создавая электрический ток.
Природа электрической проводимости у металлов обусловлена наличием кристаллической решётки, в узлах которой расположены положительные ионы, а в пространстве между ними движутся свободные электроны. Свободные электроны не связаны с ядрами своих атомов. Отрицательный заряд всех свободных электронов по модулю равен положительному заряду всех ионов решетки, таким образом проводник считается электрически нейтральным.
Кто открыл, опыт Мандельштама и Папалекси
Первые опыты по изучению электрической проводимости металлов провел немецкий ученый Карл Виктор Эдуард Рикке в 1901 году. Суть эксперимента сводилась к следующему. Три отполированных цилиндра плотно прижали друг к другу, расположив в таком порядке: медь–алюминий–медь. В течение года через них пропускали ток в одном и том же направлении.
Суммарный заряд, прошедший через этот проводник за все время составил более 3,5 МКл. После завершения опыта цилиндры взвесили и выяснилось, что их массы не изменились. Это исследование стало доказательством того, что прохождение тока в металлах не связано с химическими процессами и переносом вещества, а заряд создается частицами, которые имеются у всех металлов, т.е. электронами.
Опыты по изучению электропроводимости в 1916 году продолжили русские ученые Л. И. Мандельштам и Н. Д. Папалекси. Они задались целью узнать, имеется ли масса у электрона. Если электрон обладает массой, то должен подчиняться законам механики, в том числе, закону инерции. К примеру, если движущийся проводник резко остановить, то электроны еще какое-то время будут двигаться в том же направлении по инерции.
Была собрана следующая установка: катушка на стержне со скользящими контактами, которые присоединены к гальванометру. Катушка вращалась с большой скоростью, затем резко останавливалась, при этом фиксировали отклонение стрелки гальванометра. В ходе эксперимента ученые установили, что электрон обладает массой. Но измерить эту массу они не смогли, опыт был только качественным.
Спустя три года физики Р. Толмен и Б. Стюарт предложили свой вариант подобного эксперимента, что позволило произвести количественные измерения. Им удалось вычислить массу электрона. Для этого они измерили заряд на выходах катушки, образующийся при торможении. После внезапной остановки катушки в цепи возникал импульс тока. Направление тока указывало на то, что он вызван движением отрицательных зарядов.
С помощью баллистического гальванометра ученые измерили суммарный заряд, проходящий по цепи, и вычислили отношение заряда одной частицы к ее массе — q / m . Оно оказалось близким по значению к отношению e / m для электрона = 1 , 8 × 1011 К л / к г , которое на тот момент уже было известно.
Какие частицы его создают, скорость распространения тока
Хорошая электропроводность металлов обусловлена высокой концентрацией свободных электронов. Каждый атом металла, находящийся в узле кристаллической решетки, имеет один или несколько валентных (свободных) электронов. Валентные электроны находятся на внешней электронной оболочке и слабо связаны с ядром, поэтому атом легко с ними расстается.
Они совершают тепловое движение в различных направлениях по всему кристаллу. Положительные ионы остаются в узлах кристаллической решетки, а пространство между ними заполняется свободными электронами или так называемым электронным газом.
Если металлический проводник присоединить к источнику тока и замкнуть цепь, валентные электроны продолжают совершать хаотическое движение, но под действием возникшего внешнего электрического поля они также начинают перемещаться в одном направлении. Это упорядоченное течение электронного газа, совмещенное с тепловым движением электронов, и есть электрический ток в металле.
Скорость упорядоченного движения (дрейфовая скорость) любого электрона в проводнике не превышает 1 мм/с.
Скорость распространения электрического тока близка к скорости света в вакууме (300 000 км/с).
Одновременно с распространением электрического поля все электроны начинают двигаться в одном направлении по всей длине проводника.
Закон Ома и Джоуля-Ленца, формулы
Классическая электронная теория металлов берет за основу, что движение электронов подчиняется законам механики Ньютона. При этом не учитывают взаимодействие электронов между собой. Предполагается также, что при каждом столкновении с положительными ионами электрон передает решетке всю полученную в электрическом поле энергию, а затем начинает движение с нулевой дрейфовой скоростью.
Несмотря на эти особенности, законы электрического тока в металлических проводниках — Ома и Джоуля–Ленца — находятся в рамках классической электронной теорией.
Закон Ома
В 1827 году немецкий физик Георг Ом установил, что связь таких физических характеристик, как сила тока, напряжение и сопротивление определяется следующей зависимостью: для определенного участка цепи сила тока I прямо пропорциональна напряжению U и обратно пропорциональна электрическому сопротивлению R.
Закон Джоуля–Ленца
Так как проводник нагревается при протекании по нему электрического тока, то выделяется теплота. В 1841–1842 годах сразу два ученых независимо друг от друга Дж. Джоуль (Англия) и Э. Х. Ленц (Россия) экспериментально доказали, что количество выделяющейся теплоты Q прямо пропорционально квадрату тока I2, сопротивлению проводника R и времени t, в течение которого ток протекал по проводнику.
Q=I2Rt.
Проводник нагревается за счет работы сил электрического поля над носителями заряда. Эта работа A также равна Q: A=Q=I2Rt.
Применив закон Ома для участка однородной цепи и определение силы тока, можно получить следующие варианты формулы:
Электрический ток в металлах: подробное объяснение
Электрический ток в металлах представляет собой упорядоченное движение свободных электронов. Более подробно об этом читайте далее в нашей статье.
Важно знать
Как известно, электрический ток – это упорядоченный поток носителей электрического заряда. Носители – это заряженные частицы, способные свободно перемещаться во всем объеме тела.
В случае металлов этими частицами являются электроны, которые высвобождаются при образовании связи между атомами металла.
Известно, что металлы в твердом состоянии имеют кристаллическую структуру. Частицы в кристаллах расположены в определенном порядке, образуя пространственную решетку (кристалл).
Наконец, кристаллическая решетка металла образована положительными ионами, погруженными в “облако” хаотически движущихся так называемых свободных электронов, также называемых электронами проводимости. В зависимости от валентности атомов металла, один атом может освободить от одного до трех электронов при образовании металлических связей. Число таких высвобожденных электронов непосредственно переводится в число носителей заряда. Это является одним из факторов, влияющих на способность металла проводить электрический ток.
Доказательством того, что ток в металлах вызывается электронами, послужили эксперименты наших отечественных физиков Леонида Исааковича Мандельштама и Николая Дмитриевича Папалекси, а также американских физиков Бальфура Стюарта и Роберта Толмана.
Способность металла проводить электрический ток может быть описана физической величиной, называемой удельным электрическим сопротивлением. Эта физическая величина обозначается греческой буквой ρ (читается как “ро”). Единицей измерения удельного сопротивления является Ом · м, т.е. произведение Ом на метр. Удельное сопротивление – это константа, которая характеризует материал и имеет различные значения для разных материалов. Например, удельное сопротивление меди составляет 1.72*10 -8 Ом · м. Это означает, что электрическое сопротивление медного проводника длиной 1 метр и площадью поперечного сечения 1 м равно 1.72*10 -8 Ом . В целом, чем ниже удельное сопротивление материала, тем лучше он проводит электрический ток.
В таблице ниже приведены некоторые примеры удельного сопротивления часто используемых металлов.
| Металл | Удельное сопротивление (Ом · м) |
| Серебро | 1.59*10 -8 |
| Медь | 1.72*10 -8 |
| Алюминий | 2.82*10 -8 |
| Вольфрам | 5.6*10 -8 |
| Железо | 10*10 -8 |
Удельное электрическое сопротивление может быть связано с микроскопическими свойствами материала. В частности, он зависит от концентрации носителей заряда и их подвижности.
Движение свободных электронов в металлах не является полностью “свободным”, поскольку во время их движении они взаимодействуют с другими электронами, и прежде всего с ионами кристаллической решетки. Специфика этого движения описывается так называемой классической моделью проводимости.
Основные предположения и выводы этой модели представлены в большом упрощении ниже.
Классическая модель проводимости
Без внешнего электрического поля электроны совершают тепловые хаотические движения, сталкиваясь друг с другом, а также сталкиваясь с ионами кристаллической решетки. В результате такого движения среднее положение электронов практически не меняется (см. рис. 1.).

Рис. 1. Пример траектории электрона во время его хаотического теплового движения в металле
Из-за квантовых эффектов, и в частности из-за принципа запрета Паули, который не позволяет всем электронам занимать самое низкое энергетическое состояние, средняя скорость электронов в металлах, связанная с их хаотическим тепловым движением, больше, чем скорость частиц в классическом идеальном газе той же температуры. Она составляет порядка 10 м/с.
Если электрическое напряжение U приложено к концам проводника длиной L в нем появится электрическое поле с напряженностью E = U / L
Под действием этого внешнего поля, согласно второму закону динамики, электроны ускоряются: a = F / m,
где F = e*E – сила, с которой электрическое поле действует на электрон с зарядом e. Таким образом, ускорение электрона составляет: a = e*E / m .
Ускоренное движение электрона длится лишь довольно короткое время, пока он не столкнется с ионом
кристаллической решетки. В результате такого столкновения электрон теряет практически всю свою кинетическую энергию. Однако замедленный электрон не остается в состоянии покоя – он снова ускоряется под действием электрического поля, снова сталкивается с одним из ионов из ионы кристаллической решетки и т.д. Этот эффект добавляет к скорости тепловых движений дополнительную направленную среднюю скорость u, которая из-за отрицательного заряда электрона имеет направление, противоположное напряженности внешнего электрического поля. Эта скорость называется средней скоростью дрейфа (рис. 2).

Рис. 2. Дрейф электрона под действием внешнего электрического поля
В проводнике начинает течь электрический ток с силой тока I (см. рисунок 3).

Рис. 3. Дрейфующие электроны сталкиваются с ионами кристаллической решетки
Предполагая, что движение электрона равномерно ускоряется между столкновениями с ионами решетки, с ускорением a = e*E / m , и предполагая, что в результате столкновения электрон передает всю свою кинетическую энергию кристаллической решетке, мы можем вычислить скорость, которую развивает электрон в своем свободном движении: v = a*τ . В этой формуле τ – средний интервал времени между последующими столкновениями дрейфующего электрона с ионами кристаллической решетки.
Поскольку при равномерно ускоренном движении без начальной скорости средняя скорость является средним арифметическим начальной (равной нулю) и конечной скоростью, то получаем: u = v / 2 = e*E*τ / 2*m .
Из полученной формулы следует, что скорость дрейфа, помимо внешнего электрического поля, определяется средним интервалом времени между столкновениями электронов с ионами решетки. Этот параметр зависит от многих факторов (включая температуру, кристаллическую структуру металла, дефекты кристаллической структуры, примеси) и, как выясняется, существенно влияет на электрическое сопротивление материала.
Средняя дрейфовая скорость электронов составляет порядка 10 -4 м/с. Она очень мала по сравнению со скоростью теплового движения, которая составляет порядка 10 6 м/с.
Классическая теория проводимости достаточно хорошо описывает явление электропроводности в металлах. Однако эта теория не может объяснить экспериментально наблюдаемую зависимость электрического сопротивления от температуры.
Причина упомянутой неудачи классической теории проводимости заключается в том, что она не учитывает влияние ионов решетки на движение электронов между столкновениями. Более близкие к реальности результаты дает квантовая теория проводимости, которая описывает электроны как частицы, подверженные квантовой статистике, движущиеся в периодическом электрическом поле, создаваемом положительными ионами решетки.
Выводы простым языком
Отрицательный заряд всех свободных электронов по абсолютному значению равен положительному заряду всех ионов решётки. Поэтому в обычных условиях металл электрически нейтрален. Свободные электроны в нём движутся беспорядочно. Но если в металле создать электрическое поле, то свободные электроны начнут двигаться направленно под действием электрических сил. Возникнет электрический ток. Беспорядочное движение электронов при этом сохраняется, подобно тому как сохраняется беспорядочное движение в стайке мошкары, когда под действием ветра она перемещается в одном направлении.
« Скорость движения самих электронов в проводнике под действием электрического поля невелика – несколько миллиметров в секунду, а иногда и ещё меньше. Но как только в проводнике возникает электрическое поле, оно с огромной скоростью, близкой к скорости света в вакууме (300 000 км/c), распространяетcя по всей длине проводника. »
Перышкин А. В. Физика 8. – М.: Дрофа, 2010
Как пример, электрический сигнал, посланный, например, по проводам из Москвы во Владивосток (s = 8000 км), приходит туда примерно через 0,03 с.
Одновременно с распространением электрического поля все электроны начинают двигаться в одном направлении по всей длине проводника. Так, например, когда цепь электрической лампы замкнута, электроны в спирали лампы также движутся упорядоченно.
Сравнение электрического тока с потоком воды в водопроводной системе и распространения электрического поля с распространением давления воды поможет нам понять это. Когда вода поднимается в резервуар для воды, давление (напор) воды очень быстро распространяется по всей системе водоснабжения. Когда мы включаем кран, вода уже находится под давлением и сразу же начинает течь. Но вода, которая была в кране, течет, а вода из башни достигает крана гораздо позже, потому что вода движется с меньшей скоростью, чем распространяется давление.
Когда говорят о скорости распространения электрического тока в проводнике, то имеют в виду скорость распространения по проводнику электрического поля.
Где и как распределяются заряды в проводнике?
Проводником электричества является любое вещество, у которого присутствуют свободные отрицательные или положительные заряды. У металлов носителями зарядов являются электроны. Рассматривая вопрос о распределении зарядов в проводнике мы, по умолчанию, будем ссылаться на металлические тела. Но все выводы, касающиеся перераспределения зарядов в металлах, справедливы и для других типов веществ, с наличием свободных носителей положительных ионов.
Носители зарядов и их движение
При отсутствии электрического поля свободные точечные заряды пребывают в равновесии. Они осуществляют колебания, взаимодействуя между собой и с ионами такого же, либо противоположного знака. Однако картина равновесия вмиг нарушается при попадании металла в электрическое поле. На заряженном проводнике возникает электрическое смещение.
Под действием кулоновских сил происходит перераспределение электронов в металлическом теле. Перемещению зарядов способствует напряжённость поля, действующая на носители заряженных частиц разных знаков, но в разных направлениях.
В результате этого воздействия заряженные частицы устремляются в противоположные стороны. Точнее, в металлах происходит только перемещение электронов, которые скапливаются на поверхности с одной стороны.
Положительные ионы, связанные атомными силами кристаллической решётки не перемещаются, но поскольку электроны устремились в одну сторону, то на другой стороне проводника преобладают дырки (положительно заряженные ионы) (см. рис. 1). Таким образом, можно утверждать, что электроны и положительные ионы под действием электрического поля распределяются в противоположных направлениях на поверхности тел. То есть, заряды стремятся к равновесному распределению.

Рис. 1. Распределение зарядов в проводнике
Процесс распределения частиц продолжается до тех пор, пока не уравновесится их взаимодействие внешних и внутренних сил. То есть, пока сумма напряжённостей внешнего электрического поля не уравняется с внутренней напряжённостью. Данный процесс длится доли секунды. Если плотность энергии не меняется, а металл остаётся в спокойствии, то равновесие сил является константой.
Учитывая направления внешних векторов напряженности и внутренних сил, действующих на проводник, можно записать:
Результирующий вектор напряженности
Нулевое значение напряжённости поля означает, что внутренний потенциал тела компенсируется действием внешних сил:
Если в электрическое поле поместить металлический шар, то все статическое электричество на его поверхности будет иметь одинаковый потенциал. Такие поверхности получили название эквипотенциальных поверхностей. Заряды, скопившиеся под действием сил напряжённости поля, называются индуцированными или избыточными. Наличие избыточных зарядов характерно для всех типов проводников, оказавшихся в электрическом поле.
Рассуждения, приведённые выше, справедливы также для веществ со свободными ионами разных знаков (растворы солей и кислот). В результате такого распределения заряды также располагаются на противоположных концах токопроводящего тела. При этом равенство, записанное выше, сохраняется.
Если проводник изолирован, то до определённого времени количество индуцированного электричества будет увеличиваться, пока не восстановится новое равновесие. При этом внутренняя напряженность поля, увеличенная плотностями зарядов, будет усиливать своё противодействие. В конце концов, наступит момент, когда отталкивающие силы остановят приток одноименных статического электричества.
Если же создать условия для отвода избыточных заряженных частиц (при сохранении притока новых), например, заземлить кондуктор, то возникнет электрический ток. Причём перемещение заряженных частиц будет проходить по поверхности металла, но не внутри его, как можно было бы ожидать.
Электроемкость уединенного проводника
Рассмотрим отдельно взятый проводник, удалённый от других заряженных тел. Такие токопроводящие тела называют уединёнными. В результате электростатической индукции на поверхности уединённого проводника возникает статическое электричество. Количество индуцированных зарядов зависит от уровня напряжённости внешнего поля.
Потенциал на таком проводнике зависит от его заряда (φ): Q=Cφ, откуда
С = Q/φ , где C – электроёмкость.
Если уединённому проводнику сообщить некий дополнительный заряд, то в течение некоторого времени он будет сохраняться. Количество электричества, которые способен удержать уединённый проводник, зависит от его формы и площади поверхности. Наибольшую ёмкость имеют сферические образования, так как площадь поверхности сферы на единицу объёма самая большая.
Два уединённых проводника разделённые диэлектриком образуют конденсатор. При этом электроемкость конденсатора Cконд = Q/(φ1 – φ2), где ( φ1 – φ2 ) разница потенциалов между обкладками. Индуцированные заряды с обкладок заряженного конденсатора можно снять на нагрузку, подключённую к выводам обкладок.
Распределение зарядов и форма тела
Как было замечено выше, распределение зарядов зависит от формы тела. Больше всего статического электричества собирается на выступах, особенно на острых концах (см. рис. 3, 4).
Рис. 3. Форма тела и распределение статического электричества Рис. 4. Распределение статического электричества на кондукторе
Как видно из рисунка 4 плотность распределения зарядов на вогнутых поверхностях минимальна. Электростатическое поле сплошных и полых проводников не отличается, если их поверхности идентичны. Другими словами все токопроводящие тела с одинаковыми поверхностями обладают одинаковыми поверхностными плотностями.
На сферических поверхностях статическое электричество распределяется равномерно. Ёмкость конденсатора (сферического) вычисляют по формуле:
Емкость сферического конденсатора
где R1 и R2 – внешний и внутренний радиусы сферического конденсатора.
Распределение статического электричества на сфере иллюстрирует рисунок 5. Обратите внимание на то, что внутри сферического тела, как впрочем, и любого другого, заряды отсутствуют: вектор E=0, φ=const.

Рис. 5. Распределение заряженных частиц на сфере
Вы, наверно, слышали о клетке Фарадея. Человек, находящийся в замкнутом пространстве из токопроводящего материала, то есть в клетке, не ощущает на себе влияния мощных разрядов. Статическое электричество стекает по поверхностям стенок клетки на землю, и не могут попасть внутрь клетки.
Читайте также:
