Влияние примесей на удельное сопротивление металлов
Документ из архива "Ответы с Ириными дополнениями", который расположен в категории " ". Всё это находится в предмете "материалы и элементы электронной техники" из раздела "", которые можно найти в файловом архиве МЭИ (ТУ). Не смотря на прямую связь этого архива с МЭИ (ТУ), его также можно найти и в других разделах. Архив можно найти в разделе "к экзамену/зачёту", в предмете "материалы и элементы электронной техники" в общих файлах.
Онлайн просмотр документа "Ответы с Ириными дополнениями"
Текст 10 страницы из документа "Ответы с Ириными дополнениями"
У металлов, объем которых при плавлении уменьшается, удельное сопротивление уменьшается также скачкообразно (ветвь г; табл-12.2). У большинства металлов в расплавленном состоянии ТКр положительный (ветви д, е) и лишь у немногих ТКр отрицательный (ветвьж,г)
17. Зависимость удельного электрического сопротивления металлических проводниковых материалов от их строения и внешних факторов. Влияние частоты напряжения на сопротивление металлических проводников. Скин-эффект.
Влияние примеси на удельное сопротивление
Чистые отожженные металлы имеют менее деформированную кристаллическую решетку, поэтому для них характерны большие значения λ, и, следовательно, у (малая величина ρ). Примеси, растворенные в металлах, деформируют кристаллическую решетку и вызывают большие изменения удельного сопротивления. Отсюда ρ металлов, содержащих растворенную примесь, всегда выше, чем ρ чистых.

Рис. 12.4. Удельное сопротивление ρ меди в зависимости от концентрации N различной примеси в долях процента
Влияние деформации на удельное сопротивление
Большое влияние на удельное сопротивление и механические свойства оказывают дефекты кристаллической решетки, возникшие при холодной обработке металлов давлением (ОМД). В результате пластической деформации, вызванной холодной ОМД, зерна (и блоки в них) удлиняются и измельчаются, возрастает деформация кристаллической решетки и увеличиваются в ней дефекты: возрастает плотность дислокаций и концентрация вакансий, что приводит к улучшению механических свойств — увеличивается твердость и предел прочности на разрыв. Однако удельное сопротивление при этом также увеличивается. При рекристаллизационном отжиге металлов, подвергнутых холодной ОМД, зерна (и блоки в них) будут округляться и укрупняться, кристаллическая решетка выпрямляться, а концентрация дефектов в ней будет уменьшаться. Удельное сопротивление при этом может понизиться до первоначального значения. Одновременно понизится твердость и предел прочности на разрыв.
При упругой деформации удельное сопротивление металлов может как увеличиться, так и уменьшиться. При упругой деформации, вызванной растяжением, амплитуды тепловых колебаний узлов кристаллической решетки увеличатся, в результате уменьшится λ, и возрастет ρ. При упругой деформации, вызванной сжатием, амплитуды тепловых колебаний узлов кристаллической решетки, наоборот, уменьшатся, в результате λ возрастет, а ρ снизится.
Влияние размеров проводника на удельное сопротивления
В металлических проводниках в виде тонких пленок, фольги или проволоки образуется мелкозернистая структура. Чем мельче зерно, тем больше суммарная удельная поверхность зерен. Наиболее дефектной частью зерна является его поверхность. С уменьшением размера зерна увеличивается дефектность структуры металла и, следовательно, возрастает его удельное сопротивление р. Для тонких пленок, полученных методом термического напыления в вакууме или химического осаждения, увеличение р наблюдается при уменьшении толщины δ, начиная примерно с δ = 0,1—0,01 мкм. Увеличение удельного сопротивления объясняется тем, что при кристаллизации металла на подложке в образовавшейся мелкозернистой пленке появляются многочисленные дефекты в виде вакансий, дислокаций, межблочных и межзеренных границ, пор и др. В результате уменьшается средняя длина свободного пробега электрона λ, и р возрастает. При дальнейшем уменьшении толщины δ пленки удельное сопротивление δ продолжает расти (рис. 12.6, а).
Для сравнительной оценки удельного сопротивления тонких металлических пленок принято сопротивление квадрата RD, через противоположные грани которого ток протекает параллельно поверхности
где ρδ — удельное (объемное) сопротивление пленки толщиной δ.
Температурный коэффициент удельного сопротивления тонких металлических пленок ТКρδ может быть как положительным, так и отрицательным (см. рис. 12.6, б). При увеличении толщины пленки αρδ (ТК ρδ) стремится к значению αρ (ТКр) данного материала в толстых слоях.

Рис. 12.6. Зависимость удельного сопротивления ρδ (а) и температурного коэффициента удельного сопротивления αρδ (б) металлической пленки от ее толщины δ
Влияние частоты напряжения на сопротивление металлически проводников
Вихревые токи (токи Фуко), возникающие в металлических проводниках, по которым течет переменный ток, направлены таким образом, что ослабевают ток внутри проводника и усиливают его вблизи поверхности. В результате высокочастотный ток оказывается распределенным по сечению проводника неравномерно — большая его часть сосредоточивается у поверхности проводника. Это явление называют скин-эффектом. Из-за скин-эффекта внутренняя часть проводников в высокочастотных цепях оказывается бесполезной. Поэтому в высокочастотных цепях проводники могут быть полыми.
Скин-эффект характеризуется глубиной проникновения электромагнитного поля в металлический проводник: чем выше частота поля, тем на меньшую глубину оно проникает в проводник. С увеличением глубины проникновения поля плотность тока уменьшается по экспоненте. Глубину, на которой амплитуда электромагнитной волны затухает в е раз (до -37%), называют глубиной проникновения поля ∆. Величина ∆ зависит от частоты напряжения ω, удельной электропроводности γ и магнитной проницаемости μ:
где а — коэффициент затухания электромагнитной волны; μo — магнитная постоянная.
Сопротивление проводника, вызванное скин-эффектом, можно оценить сопротивлением квадрата его поверхности Rs, Ом, аналогично рассчитываемому R□ по формуле (12.9), заменив δ на ∆:
Из выражения (12.11) следует, что сопротивление Rs плоского проводника при скин-эффекте равно сопротивлению плоского проводника толщиной ∆ при постоянном токе.
Зависимость Rs и ∆от частоты поля для. некоторых важнейших металлов и сплавов высокой проводимости приведены на рис. 12.7.

Рис. 12.7. Зависимость сопротивления при скин-эффекте Rs и глубины проникновения поля ∆ от частоты для плоских проводников. Значения Rs и ∆ по нижней шкале частоты отсчитываются непосредственно; по верхней шкале частоты значение Rs умножается на 10 —2 , а ∆ - 10 —2
18. Высокоомные сплавы и их свойства. Удельное сопротивление металлических сплавов.
Удельное сопротивление металлических сплавов
У металлических сплавов удельное сопротивление зависит не только от концентрации компонентов, образующих данный сплав, но и от типа образовавшегося сплава. В зависимости от физико-химического взаимодействия компонентов друг с другом (от соотношения размеров их атомов и электрохимических констант) могут образовываться следующие основные типы сплавов:
гетерогенные структуры (механические смеси),
твердые растворы с неограниченной или ограниченной растворимостью компонентов друг в друге в твердом состоянии,
химические (интерметаллические) соединения.
Рассмотрим диаграммы состояния каждого из перечисленных типов сплавов и характер зависимости удельного сопротивления и механических свойств от состава сплавов.
В электро- и радиотехнике большой интерес представляют
сплавы, образующие твердые растворы; их широко применяют в производстве проволочных резисторов, реостатов, термопар и др.
При образовании сплава твердый раствор постоянная кристаллической решетки металла-растворителя изменяется, атомы компонентов распределяются по ее узлам беспорядочно. В результате кристаллическая решетка существенно деформируется, что приводит к сильному рассеянию электронов проводимости и увеличению удельного сопротивления. Чем больше разница в значениях валентности металла-растворителя и растворенного металла и в размерах их атомов, тем больше увеличивается удельное сопротивление. Зависимость ρ от состава сплавов, образующих твердые растворы проходит через максимум (см. рис. 10.9, б).
Максимальное значение р проявляется у сплавов, кристаллическая решетка которых максимально деформирована. При этом могут наблюдаться два типа максимума. Если сплавляемые металлы, образующие твердые растворы, принадлежат к одной группе периодической системы элементов Д.И. Менделеева, то зависимость р от состава сплавов обычно имеет примерно симметричный максимум. Если оба сплавляемых металла принадлежат к разным группам периодической системы элементов, то максимум зависимости р от состава имеет несимметричную форму и сдвинут от середины диаграммы в сторону металла, удельное сопротивление которого при комнатной температуре больше.

19. Влияние примеси на удельное сопротивление. Влияние размеров проводника на удельное сопротивление. (Пленочные проводники в микросхемах).
Ч Гетерогенные структуры (механические смеси), твердые растворы с неограниченной или ограниченной растворимостью компонентов друг в друге в твердом состоянии, химические (интерметаллические) соединения. Максимальное значение р проявляется у сплавов, кристаллическая решетка которых максимально деформирована.
В Увеличение удельного сопротивления объясняется тем, что при кристаллизации металла на подложке в образовавшейся мелкозернистой пленке появляются многочисленные дефекты в виде вакансий, дислокаций, межблочных и межзеренных границ, пор и др. В результате уменьшается средняя длина свободного пробега электрона λ, и р возрастает. Для сравнительной оценки удельного сопротивления тонких металлических пленок принято сопротивление квадрата RD, через противоположные грани которого ток протекает параллельно поверхности RD = ρδ /δ.
Свойства проводниковых материалов и зависимость их от состава и внешних факторов
К основным свойствам проводниковых материалов относятся:
- Удельная проводимость или обратная ей величина – удельное сопротивление;
- Температурный коэффициент удельного сопротивления;
- Удельная теплопроводность;
- Контактная разность потенциалов и термоэлектродвижущая сила;
- Предел прочности при растяжении и относительное удлинение при разрыве.
Удельное сопротивление проводников. Величину, обратную удельной проводимости g называют удельным сопротивлением r и для проводника с постоянным поперечным сечением определяют по формуле:
Единицей удельного сопротивления в СИ является Ом×м, однако в практике чаще пользуются внесистемной единицей мкОм×м.
Следует отметить, что в отличие от диэлектриков диапазон удельных сопротивлений металлических проводников достаточно мал – от 0,016мкОм×м. для серебра и примерно до 10 мкОм×м. для железо-хромо-кобальто-алюминиевых сплавов, т.е. занимает всего три порядка.
Температурная зависимость удельного сопротивления металлических проводников. Как было показано ранее в идеально чистых металлах единственной причиной, которая ограничивает длину свободного пробега, являются тепловые колебания узлов кристаллической решетки (фононы). Удельное сопротивление металла, обусловленное этим фактором, обозначим как ρТ.. С ростом температуры возрастают амплитуды фононов и связанные с этим флюктуации периодического поля решетки. Это повышает рассеивание электронов, уменьшает длину свободного пробега и вызывает возрастание удельного сопротивления. Для упрощенной одномерной модели решетки длина свободного пробега электронов определяется как:
где λсв - длина свободного пробега;
Δa - амплитуда фононов;
N - концентрация атомов в металле.
Потенциальная энергия атома, отклоненного на Δa от узла решетки:
где Купр - коэффициент упругости связи.
Согласно классической статистике средняя энергия одномерного гармоничного осциллятора равняется КТ. Тогда:
½ · Kупр (Δa) 2 = КТ (4.6)
где К - постоянная Больцмана.
Тогда из (4.5), (4.6) получим:
Если подставить (4.7) в (4.2) получим:
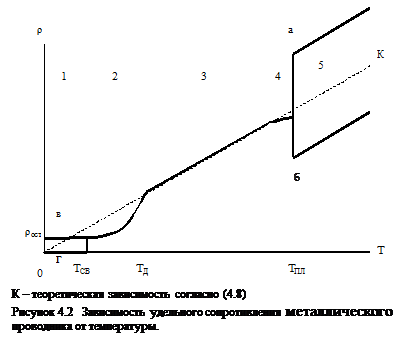
То есть с ростом температуры удельное сопротивление чистых металлов должно возрастать линейно. В действительности эта зависимость является более сложной (рисунок 4.2)
На участке 3 при комнатных температурах зависимость ρ = ¦(Т) линейна, как это видно из (4.8). То есть с ростом температуры возрастает амплитуда тепловых колебаний узлов кристаллической решетки, что уменьшает длину свободного пробега электронов.
На участке 4 вблизи температуры плавления имеет некоторая нелинейность, что объясняется другими механизмами рассеивания электронов.
При переходе металла из твердого состояния в жидкое (температура плавления Тпл) может иметь место как резкое возрастание удельного сопротивления (а), так и его уменьшение (б). Это связано с изменением структуры кристаллической решетки. Если при плавлении объем металла возрастает, что имеет место для большинства металлов, то расстояние между атомами тоже возрастает, металлическая связь уменьшается, а амплитуда фононов возрастает, что уменьшает длину свободного пробега электронов, следовательно, сопротивление металла возрастает. Для некоторых металлов (висмут, галлий) при плавлении объем металла уменьшается, что усиливает связи между атомами, амплитуда фононов уменьшается и удельное сопротивление тоже уменьшается.
На участке 5 металлы находятся в жидком состоянии и сохраняют кристаллическую решетку, поэтому зависимость удельного сопротивления от температуры поясняется аналогично участку 3.
На участке 2, ниже температуры Дебая (ТД) изменяется частота тепловых колебаний узлов кристаллической решетки, поэтому зависимость ρ = ¦(Т) нелинейна и подчиняется закону:
ρ = A·T n (4.9)
где n - изменяется от 1 до 5.
На участке 1 некоторые металлы имеют конечное сопротивление (rост) даже при температуре Т=0 К. Это объясняется наличием в металле статических дефектов решетки, прежде всего примесей. Это позволяет оценивать чистоту металлов на основании отношения:
где ρ300K , ρ4K - соответственно удельное сопротивление металла при 300 К и 4,2 К (температура кипения жидкого гелия). Чем меньше это отношение, тем чище металл.
У некоторых металлов при температуре ниже Тсв наблюдается резкое уменьшение удельного сопротивления до нуля. Такое явление называют сверхпроводимостью.
Таким образом, согласно (4.9) металлические проводники в обычных условиях имеют линейную зависимость удельного сопротивления от температуры.
Влияние примесей на удельное сопротивление металлических проводников.Как уже говорилось, причинами рассеяния электронов в металлах являются не только тепловые колебания узлов кристаллической решетки, но и наличие статических дефектов, которые, прежде всего связанные с примесями. Рассеивание на статических дефектах не зависит от температуры. Поэтому при абсолютном нуле сопротивление реальных металлов остается конечным. Из этого следует правило Маттиссена об аддитивности удельного сопротивления:
где ρпр - полное сопротивление металла с примесью;
ρт - сопротивление, обусловленное рассеянием электронов на фононах;
ρост - остаточное сопротивление, обусловленное рассеиванием электронов на статических дефектах решетки.
Наибольший вклад в остаточное сопротивление вносит рассеяние на примесных атомах, которые практически всегда имеются в металлах. Поэтому длина свободного пробега электронов в металлах с примесью состоит из:
где lТ, lД - длина свободного пробега электронов, ограниченная фононами и примесями, соответственно.
Длина пробега lД:
где Nd - концентрация атомов примеси;
Sd – эффективная плоскость рассеивания электронов атомами примеси.
Тогда удельное сопротивление проводника с примесью:
То есть наличие примесь увеличивает удельное сопротивление металла, но его зависимости от температуры остается линейной (рис. 4.3)
Dρост = а +b(DZ) 2 (4.14)
где Dρост - изменение остаточного сопротивления при изменении примеси;
DZ - разность валентностей собственного атома и атома примеси;
а, b - константы.
Таким образом, на сопротивление металлов меньшее влияние оказывают примесные атомы металла, а большее – атомы металлоидов.
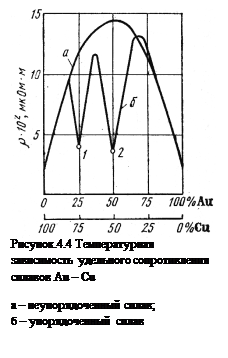
В технике очень широко используют металлические сплавы, имеющие значительную концентрацию атомов примеси, со структурой неупорядоченного твердого раствора. Статическое распределение атомов разного вида в узлах кристаллической решетки вызывает значительные флюктуации периодического поля кристалла, рассеивающего электроны. Но в неупорядоченных твердых растворах, преимущественно с добавкой примеси, изменяется только период решетки. Поэтому действителен закон Нордгейма:
де С - константа;
xА, xВ - атомные доли компонентов в сплаве.
То есть в бинарных твердых растворах А-В остаточное сопротивление возрастает, как при добавлении атомов металла В к металлу А, так и при добавленные атомов металла А к металлу В (рис. 4.4). Остаточное сопротивление достигает максимума при xА = xВ = 0,5.
Закон Нордгейма описывает изменение остаточного сопротивления для непрерывных неупорядоченных твердых растворов. Если сплав отжечь, то он может стать упорядоченным и, если при этом возникают интерметаллические соединения, которые имеют собственную кристаллическую решетку, то зависимость остаточного сопротивления разделяется на части, соответственно числу интерметаллических соединений. Таким образом, удельное сопротивление металлических сплавов всегда выше сопротивления чистых металлов. Это свойство используется для получения высокоомных проводниковых материалов.
Изменение удельного сопротивления при упругих деформациях объясняется изменением амплитуды колебания узлов кристаллической решетки металла. Увеличение амплитуды колебания узлов решетки металла приводит к уменьшению длины свободного пробега носителей заряда и удельное сопротивление возрастает. Пластическая деформация, как правило, повышает удельное сопротивление металлов вследствие искажения кристаллической решетки. При рекристаллизации путем термической обработки (отжига) удельное сопротивление может вновь снижено до первоначальных значений.
Температурный коэффициент удельного сопротивления.В диапазоне температуры, где зависимость r от t близка к линейной (рис. 4.2, участок 3) допустима линейно-кусочная аппроксимация этой зависимости, и величина удельного сопротивления в конце диапазона температуры t может быть подсчитана по формуле
где r0—удельное сопротивление в начале диапазона.
Величину ar из выражения (4.) называют средним температурным коэффициентом удельного сопротивления в данном диапазоне температуры:
Дифференциальное выражение для ar имеет вид
Значения ar чистых металлов в твердом состоянии близки друг к другу, и поэтому приближенно можно считать ar » 0,004 , К -1 .
Исключение составляют элементы, относящиеся к ферромагнетикам — железо, никель, кобальт, гадолиний, а также натрий, калий, хром и др., однако и для них ar отличается от приведенной величины только в 1,5—2 раза.
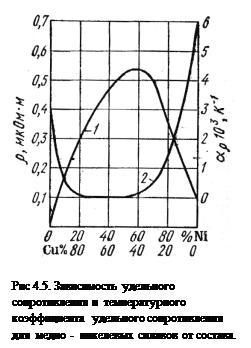
Наличие примесей уменьшает значение αρ. У некоторых сплавов αρ. даже может приобретать небольшие отрицательные значения (рис.4.5). Это объясняют тем, что при более сложных составе и структурax по сравнению с чистыми металлами сплавы нельзя рассматривать как классические металлы, т. е. изменение проводимости их обусловливается не только изменением подвижности носителей заряда но в некоторых случаях и частичным возрастанием концентрации носителей при повышении температуры. Сплав, у которого уменьшение подвижности с увеличением температуры компенсируется возрастанием концентрации носителей заряда, имеет нулевой температурный коэффициент удельного сопротивления.
Это явление используется для изготовления термостабильных сплавов, например, константана, манганина ). Константан - сплав с 60% Ni и 40% Сu имеет большое сопротивление (~0,5 мкОм×м) и очень малый температурный коэффициент (меньше 10 -6 К -1 ), отсюда и его название.
Удельная теплопроводность металлов. Высокая теплопроводность металлов легко объясняется посредством передачи тепловой энергии атомов нагретого участка металла атомам холодного участка за счет переноса этой энергии коллективизированными электронами. Так как механизм электропроводности и теплопроводности в металлах обусловлен одними и теми же факторами: движением электронного газа и его плотностью, очевидно, что металлы с высокой электропроводностью являются также хорошими проводниками тепла, а диэлектрики обладают не только низкой электропроводностью, но и низкой теплопроводностью. Так, медь имеет удельную теплопроводность 406 Вт/К×м, серебро 453 Вт/К×м, алюминий 218 Вт/К×м, что значительно выше чем у диэлектриков. Удельная теплопроводность и электропроводность металлов связаны законом Видемана-Франца:
где lТ - удельная теплопроводность.
σ - удельная электропроводность.
L0 - число Лоренца.
Поскольку на участке комнатных температур удельная электропроводность падает пропорционально температуре, то согласно (4.19), удельная теплопроводность металлов не должна зависеть от температуры. Это следствие из закона Видемана-Франца выполняется для большинства металлов. Это свойство применяют в технике, при использовании металлов как радиаторов для охлаждения мощных полупроводниковых приборов.
Для этой цели необходимо использовать металлы с большим значением удельной теплопроводности. Чаще всего, это сплавы на основе алюминия (силумин), которые имеют хорошие тепловые, механические и антикоррозийные свойства. Медь нельзя использовать вследствие её плохой коррозионной стойкости, а серебро - вследствие высокой стоимости.
Контактные явления и термоэлектродвижущая сила (термо-э.д.с.)
При соприкосновении двух разных металлов, между ними возникает контактная разность потенциалов. Согласно квантовой теории причиной этого является различная энергия Ферми соприкасающихся металлов. Пусть в изолированном состоянии электронный газ в металлах А и В имеет энергию Ферми WF A и WF B , отсчитываемую от дна зоны проводимости (рис.4.6).
Термодинамическая работа выхода электронов из металла равняется, соответственно, cА и cВ. Поскольку кинетическая энергия электронов, которые находятся на уровне Ферми в разных металлах различна, то при контакте материалов возникает значительный переход электронов из металла В с большим значением энергии Ферми в металл, где эта энергия меньше. Например, из металла В в металл А. Вследствие этого металл В заряжается положительно, а металл А - отрицательно. Между ними возникает разность потенциалов, которая блокирует дальнейший переход носителей заряда. Равновесие наступит, если:
где UK - контактная разность потенциалов.
контактная разность потенциалов достигает несколько вольт.
Термоэлемент, который построен из двух различных металлических проводников с замкнутой цепью, называют термопарой (рис.4.7).
Вольтметр в такой цепи будет показывать разность потенциалов, которую называют термоэлектродвижущей силой (термо-э.д.с.). Термо-э.д.с. равняется:
где aT — относительная удельная термо-э.д.с.
Значение aT зависит от природы материалов и температуры и включает в себя три составляющих. Первая обусловлена температурной зависимостью контактной разности потенциалов, поскольку с ростом температуры уровень Ферми в металлах незначительно, но смещается.
Вторая составляющая обусловлена диффузией носителей заряда от горячих спаев к холодным. Поскольку существует градиент температуры от контакта к контакту, то возникает диффузия электронов от горячего контакта к холодному, что дает некоторый вклад в возникающую разность потенциалов.
Третья составляющая возникает вследствие захвата электронов квантами тепловой энергии. Их поток тоже передвигается к холодному контакту. Значение aT приблизительно равняется нескольким мкВ/К.
Термопары часто используют для измерения температуры. Если температуру холодного контакта поддерживать 0 О С, то вольтметр будет показывать напряжение пропорциональное температуре горячего контакта. Достоинством термопар является высокая линейность, возможность измерения температуры в широком интервале температур, независимость значения термо-э.д.с. от длины проводников.
Вследствие того, что значение aT зависит от состава материала и незначительно от температуры, термопары градуируют, используя точки плавления металлов: свинца, олова, серебра и других.
Наиболее распространенными термопарами являются:
· Хромель- копель (типа ХК). Она позволяет измерять температуры до 600 О С и имеет при этой температуре термо-э.д.с. приблизительно 50 мВ.
· Хромель-алюмель (типа ХА). Она используется к температурам 1000 О С и имеет при этой температуре термо-э.д.с. приблизительно 40 мВ.
· Медь-константан. Ее используют при низких температурах до 350 О С. При этой температуре термо-э.д.с. достигает 15 мВ.
· Платинородий-платина (типа ПП или ППР). Ее применяют до температуры 71600 О С. Термо-э.д.с. у этой термопары невелика (приблизительно 14 мВ при 1600 О С). Но она позволяет обеспечить наиболее точные и стабильные измерения температуры.
Однако явление термо-э.д.с. имеет и отрицательные стороны. В реальных условиях исключить градиенты температур практически невозможно. Поэтому, если контактируют различные металлы, то возможно возникновение паразитной термо-э.д.с. Для устранения этого в цепях (прежде всего электроизмерительных устройств), надо подбирать контактирующие металлы с малыми значениями термо-э.д.с. Такой парой, например, является медь-манганин.
2.1.3. Влияние примесей и дефектов структуры на удельное сопротивление металлов
Примеси вносят наиболее существенный вклад в величину остаточного сопротивления. Атомы любого примесного элемента повышают ρ , даже если сама примесь обладает большей электропроводностью.
Рассеяние электронов проводимости на атомах примеси тем сильнее, чем больше разница в валентности примесного элемента и металла - растворителя ∆ Z : ρ ост ~ ∆ Z 2 . Так что металлоидные примеси на снижение проводимости оказывают более сильное влияние, чем металлические элементы.
Дефекты структуры - вакансии, атомы в междоузлии, дислокации, границы зерен и субзерен, прочие несовершенства кристаллического строения вносят определенный вклад в ρ ост . Например, увеличение точечных дефектов в меди на 1 ат.% увеличивает ρ ост в среднем на 0,01 мкОм·м. Чем выше плотность дефектов, тем больше удельное сопротивление.
На удельное сопротивление металлических материалов влияет термообработка . Так, при закалке стали образуется неравновесная структура с большими искажениями кристаллической решетки и внутренними напряжениями. Плотность дефектов по всему объему кристалла резко возрастает, что приводит к значительному росту удельного сопротивления. При отжиге металлов и сплавов создается термодинамически устойчивая равновесная структура, внутренние напряжения исчезают, плотность дефектов уменьшается до минимума (в 2 раза и более), поэтому ρ ост резко снижается.
Пластическая деформация вызывает увеличение плотности дефектов и снижение проводимости. Для чистых металлов это снижение составляет несколько процентов, для них пластическую деформацию можно использовать как способ упрочнения без существенных потерь в электропроводности. Для металлических сплавов снижение электропроводности в результате наклепа может составлять до 25%. Для восстановления электропроводности после пластической деформации проводят рекристаллизационный отжиг.
2.1.4. Удельное сопротивление металлических сплавов
Электрическое сопротивление сплава всегда выше, чем сопротивление любого его компонента. Характер изменения электропроводности сплава зависит от фаз и структур в сплаве, что определяется диаграммой состояния.
В сплавах со структурой твердых растворов ρ ост может значительно превосходить тепловую составляющую ρ т . Для большинства твердых растворов с неограниченной растворимостью (AuAg, Ag-Cu, Cu-Au и др.) изменение остаточного сопротивления в зависимости от состава сплава хорошо описывается параболической функцией в соответствии с законом Нордгейма (рис. 4):
ρ ост = c x A x B = c x A ( 1− x A ) ,
где х А , х В - атомные доли компонентов в сплаве; с - постоянная, зависящая от природы сплава.
Рис. 4. Диаграмма состояния Cu-Au (а) и зависимости ρ и α ρ
от состава сплава (б)
Если ни один из компонентов не является переходным металлом, то ρ max и α ρ min соответствует 50%-ному соотношению компонентов х А = х В = 0,5 (рис. 4). Если один из компонентов относится к металлам переходных групп, как, например, в сплавах Cu-Ni, то характер изменения ρ и α ρ имеет некоторые особенности (рис. 5):
• ρ max существенно выше, чем в системе с непереходными металлами, что связано с переходом части валентных электронов на незаполненные уровни внутренней d -оболочки переходного
металла и уменьшением концентрации электронов проводимости;
• ρ max и α ρ min не соответствуют 50%-ному соотношению компонентов;
• α ρ достигает в некоторых сплавах нулевых и даже отрицатель-
Сплавы со структурой твердых растворов используют как проводниковые материалы высокого удельного сопротивления для изготовления резисторов и нагревательных элементов.
Рис. 5. Диаграмма состояния Cu-Ni (а) и зависимости ρ и α ρ
В сплавах с гетерофазной структурой - при образовании эвтектик, эвтектоидов, включений вторичных фаз удельное сопротивление, согласно правилу Н.С.Курнакова, в первом приближении линейно изменяется с изменением состава сплава. Такие сплавы сохраняют высокую электрическую проводимость, близкую к проводимости чистых металлов, но по сравнению с чистыми металлами могут обладать более высокими механическими и технологическими свойствами. Так, сплавы с выделениями дисперсных фаз имеют повышенную твердость, а эвтектические сплавы - высокую жидкотекучесть и литейные свойства. У многих сплавов часто наблюдаются отклонения от линейной зависимости ρ из-за структурной неоднородности.
При образовании в сплаве промежуточных фаз или химических соединений удельное сопротивление резко изменяется. Химические соединения с металлическим типом связи (интерметаллидные электронные соединения, фазы внедрения) достаточно
электропроводны. При упорядоченном расположении атомов проводимость резко возрастает, так как восстанавливается периодичность кристаллической решетки и увеличивается длина свободного пробега электронов. В химических соединениях с ионной и ковалентной связью удельное сопротивление возрастает из-за дефектности структуры.
2.1.5. Электросопротивление тонких металлических пленок
Металлические пленки, наносимые на диэлектрическую или полупроводниковую подложку, широко используются в микроэлектронике. По выполняемым функциям различают резистивные пленки (тонкопленочные резисторы) и высокопроводящие пленки (контактные площадки, межэлементные соединения, обкладки конденсаторов).
Методы получения тонких пленок:
• термическое испарение металла с последующей конденсацией на подложку;
• испарение электронным лучом;
• катодное или ионно-плазменное осаждение;
Современные технологии позволяют получать пленки толщиной
от десятых долей микрометра до нескольких десятков нанометров. В зависимости от условий осаждения (конденсации) может сформироваться различная структура пленки от аморфного состояния до монокристаллического строения. Размерный и структурный факторы обусловливают существенные отличия электрических свойств тонких пленок от свойств объемных металлов. Особенно сильно проявляется размерный эффект в том случае, когда толщина пленки соизмерима с длиной свободного пробега электронов.
На рис. 6 показаны зависимости электрических характеристик от толщины пленки, где можно выделить три области:
I - Малой толщине пленки (δ = 10 -3 …10 -2 мкм) соответствует высокое значение ρ и отрицательное значение α ρ . Это объясняется тем, что на ранних стадиях конденсации пленка имеет островковую структуру, т.е. она не сплошная. Сопротивление такой пленки во многом определяется поверхностным сопротивлением участков ди-
электрической подложки. Для таких пленок характерно понижение ρ с увеличением температуры (α ρ < 0), как у диэлектриков.
Рис. 6. Зависимости ρ и α ρ от толщины тонкой металлической пленки
II - При толщине пленки δ = 10 -2 …10 -1 мкм диэлектрические промежутки между островками осажденного металла исчезают, пленка становится сплошной, а α ρ уже выше нуля. Однако удельное электросопротивление пленки еще велико из-за высокой концентрации дефектов, образующихся в процессе роста пленки (вакансии, дислокации, границы зерен и примесные атомы), поглощаемых из газовой среды при конденсации металла.
III - При δ > 0,1 мкм сопротивление пленки близко к сопротивлению массивного образца, структура пленки и размерный эффект уже не оказывают значительного влияния на электрические свойства.
Для оценки проводящих свойств тонких пленок пользуются параметром удельного поверхностного сопротивления или сопро-
тивления квадрата R □ , Ом.
где ρ δ - удельное сопротивление пленки толщиной δ.
Сопротивление квадрата часто используют для определения сопротивления тонкопленочного резистора
3. Влияние примеси на удельное сопротивление проводников
Поскольку удельное сопротивление металлов определяется в основном длиной свободного пробега электронов, то он будет зависеть от совершенства кристаллической решетки вещества. При введении примеси в металл электроны подвергаются дополнительному рассеянию на статических дефектах кристаллической решетки, которое не зависит от температуры. Поэтому по мере приближения температуры к абсолютному нулю сопротивление металлов стремится к некоторому постоянному значению, называемому остаточным сопротивлением. Отсюда вытекает правило Маттиссена об аддитивности удельного сопротивления:
ρпр = ρТ + ρост (3.12)
т.е. полное сопротивление металла есть сумма сопротивлений, обусловленное рассеянием на тепловых колебаниях узлов кристаллической решетки, ρТ и остаточного сопротивления ρост, вызванного рассеянием электронов на статических дефектах структуры. Общая длина свободного пробега электрона в этом случае определяется так:

(3.13)

(3.14)
а λТ определяется из (3.9).
Здесь Nпр, - концентрация примесных атомов; Sпр - сечение эффективного рассеяния примесного атома.
С учетом (З.9), (3.10), (3.12), (3.14) запишем

(3.15)
Эти зависимости иллюстрирует рис. 3.3, из которого вытекает, что температурные зависимости удельного сопротивления чистого металла и его сплавов с низким содержанием примеси взаимно параллельные.
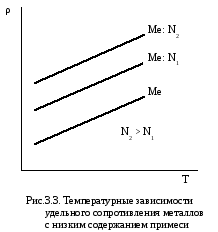
Втехнике часто применяются металлические сплавы, которые имеют структуру неупорядоченного твердого раствора, со значительным содержанием примеси. Для таких сплавов изменение остаточного удельного сопротивления описывается законом Нордгейма
ρост = СХАХВ = СХА(1 – ХА) =
= СХВ(1 – ХВ) (3.16)
где С - постоянная; ХА, ХВ - атомные части компонентов в сплаве. Из этого закона вытекает, что в бинарных твердых растворах А - В остаточное сопротивление увеличивается как при добавлении атомов А к металлу В, так и атомов В к металлу А. Остаточное сопротивление достигает своего максимального значения при равном содержании каждого компонента (рис. 3.4).

Чем выше содержание примеси в сплаве, тем меньше его температурный коэффициент удельного сопротивления. Это вытекает из того, что в твердых растворах ρост, как правило, существенно выше ρТ и не зависит от температуры. Поэтому


обычно ρост > ρТ, поэтому . На этом основано получение термостабильних сплавов (см. рис. 3.4).
4. Классификация проводниковых материалов
Проводниковые материалы можно разделить на три основные группы:
1. Материалы высокой электрической проводимости.
2. Материалы высокого удельного сопротивления.
3. Неметаллические проводники.
К первой группе относятся проводники с удельным сопротивлением менее 0,1 мкОмּм. Основное их применение - монтажные и обмоточные провода, распределительные шины и т.д. Поэтому основные требования к параметрам материалов этой группы следующие:
Малое удельное сопротивление - для уменьшения потерь.
Стойкость к коррозии - для эксплуатации материалов при различных внешних воздействиях.
Низкий удельный вес - для облегчения веса устройств.
Дешевизна и технологичность.
Относительная легкость пайки или сварки - для уменьшения переходного сопротивления в местах контактов.
Наиболее этим требованиям удовлетворяют медь и алюминий, а также их сплавы (латунь, бронза, альдрей).
Ко второй группе относятся проводники с удельным сопротивлением больше 0,3 мкОмּм. Их применение связано с изготовлением образцовых резисторов и нагревательных устройств.
Требования к материалам для образцовых резисторов:
Высокое удельное сопротивление - для уменьшения габаритов изделия.
Малое значение температурного коэффициента удельного сопротивления - для повышения термостабильности резистора.
Малое значение термоЭДС относительно меди - для уменьшения паразитных сигналов в резисторе.
Наиболее указанным требованиям удовлетворяют константан (сплав 60% меди, 40%" никеля) и манганин (сплав 86% меди, 12% марганца, 2% никеля). У первого существенно ниже температурный коэффициент удельного сопротивления, а у второго - термоЭДС относительно меди.
Требования к материалам для нагревательных элементов:
Выcoкое удельное сопротивление - для достижения необходимой температуры в малом объеме.
Наличие крепкого и стойкого оксида. В противном случае материал будет быстро разрушаться (например, вольфрам при работе на воздухе).
Температурные коэффициенты линейного расширения оксида и сплава должны быть близкими по значению. Иначе при нагревании произойдет растрескивание оксида и постепенное разрушение материала.
Этим требованиям в наибольшей степени удовлетворяют сплавы типа нихрома (никеля-хрома).
К третьей группе относятся в первую очередь проводящие модификации углерода: графит, пиролитический углерод. Электроугольные изделия широко применяются как скользящие токосъемники в электродвигателях и генераторах.
15) Влияние примесей на удельное сопротивление металлов.
Причинами рассеяния электронных волн в металлах являются не только тепловые колебания узлов решетки, но и статические дефекты структуры в том числе вызванные наличием примеси, которые нарушают периодичность потенциального поля кристалла. Такое рассеяние не зависит от Т. Поэтому при Т→ 0 сопротивление реальных металлов стремится к некоторому постоянному значению называемому остаточным сопротивлением. Отсюда вытекает правило Матиссена об аддитивности удельного сопротивления:
т.е. полное сопротивление металла есть сумма сопротивления, обусловленного рассеянием на тепловых колебаниях узлов кристаллической решетки, и остаточного сопротивления, обусловленного рассеянием электронов на статических дефектах структуры.
Исключение из этого правила составляют сверхпроводящие металлы, в которых сопротивление исчезает ниже некоторой кристаллической температуры.
Наиболее существующий вклад в остаточное сопротивление вносят – примеси, которые всегда присутствуют в реальном проводнике либо в виде загрязнения либо в виде легирующего (т.е. преднамеренно вводимого) элемента. Любая добавка, даже если она обладает повышенной проводимостью по сравнению с основными металлами приводит к повышению . Так введение в медь 0,01 атома примеси серебра вызывает увеличение на 0,02 мкОм-м.
16)Удельное сопротивление измеряется в ом-метрах. Для различных металлов скорости хаотического теплового движения электронов (при определенной температуре) примерно одинаковы. Незначительно различаются также и концентрации свободных электронов (например, для меди и никеля это различие меньше 10 %). Поэтому значение удельной проводимости (или удельного сопротивления) в основном зависит от средней длины свободного пробега электронов в данном проводнике (которая, в свою очередь, определяется структурой проводникового материала). Все чистые металлы с наиболее правильной кристаллической решеткой характеризуются наименьшими значениями удельного сопротивления; примеси, искажая решетку, приводят к увеличению (К такому же выводу можно прийти, исходя из волновой природы электронов.) Рассеяние электронных волн происходит на дефектах кристаллической решетки, которые соизмеримы с расстоянием около четверти длины электронной волны. Нарушения меньших размеров не вызывают заметного рассеяния волн. В металлическом проводнике, где длина волны электрона около 0,5 нм, микродефекты создают значительное рассеяние, уменьшающее подвижность электронов, и, следовательно, приводит к росту удельного сопротивления.
17)Тонкие" плёнки, толщины которых обычно имеют нанометровые размеры, могут существенно отличаться по свойствам от массивных образцов. Это открывает широкие возможности создания на поверхности изделий покрытий (плёнок), представляющих собой принципиально новые как по структуре, так и по свойствам материалы.
Исследования в этом направлении, относящиеся к области "инженерии поверхности", интенсивно развиваются. На базе использования плёнок возникли такие направления в технике как тонкоплёночная электроника, специальные разделы оптики. В принципе, через "тонкие" плёнки возможна практическая реализация нанокристаллического состояния материалов с целью достижения износостойкости, коррозионной стойкости и других качеств.
Установлено, что медная пленка толщиной приблизительно 5 нм состоит из кристаллитов, которые существуют в виде отдельных колоний и не образуют сплошного покрытия. Средний размер кристаллитов составляет 0,05 мкм. Наблюдается значительный разброс в размерах отдельных кристаллитов, достигающий 0,025 мкм. Медная пленка толщиной 13 нм является уже сплошной и состоит из крупных кристаллов со средним размером 0,24 мкм. Более толстая пленка (21 нм) имеет крупный размер кристаллитов - 0,81 мкм. Увеличение размера кристаллитов наблюдается с ростом толщины пленки до 60 нм. Далее размер кристаллитов остается практически постоянным.
Зависимость среднего размера кристаллитов (D) от толщины плёнки (h).
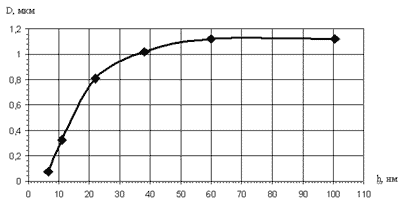
Зависимость удельного электрического сопротивления от толщины медной пленки представлена на рис.

Можно видеть, что оно определенным образом коррелирует (статистическая взаимосвязь двух или нескольких случайных величин, либо величин, которые можно с некоторой допустимой степенью точности считать таковыми) с изменением среднего размера кристаллитов в зависимости от толщины пленки. При толщине пленки более 60 нм она ведет себя подобно массивному электрическому проводнику, т.е. удельное электрическое сопротивление не зависит от масштабного фактора - толщины пленки. При толщинах пленки менее 60 нм ее с полным основанием можно относить к разряду "тонких" пленок, т.к. константа материала - удельное электрическое сопротивление оказывается зависимым от толщины пленки. С ее уменьшением резко возрастает электрическое сопротивление. При толщине пленки 13 нм удельное электрическое сопротивление становится более чем на порядок выше в сравнении с "толстой" пленкой. Высокое электрическое сопротивление "тонких" пленок обуславливается дополнительным рассеянием электронов на границах пленок, если толщина их соизмерима с длиной свободного пробега электронов проводимости. Рассеяние электронов возникает также на границах кристаллитов, тем более, когда их размеры - нанометровые, и, следовательно, граничная область с неупорядоченным расположением атомов занимает значительный объем пленки.
18) Термо-эдс-явление прямого преобразования теплоты в электричество в твердых или жидких проводниках, а также обратное явление прямого нагревания и охлаждения спаев двух проводников проходящим током. Эффект Зеебека — явление возникновения ЭДС в замкнутой электрической цепи, состоящей из последовательно соединённых разнородных проводников, контакты между которыми находятся при различных температурах.
Какие условия: 1)Разнородные проводники. 2)Контакты находятся в разных температурах.
Величина возникающей термоэдс зависит только от материала проводников и температур горячего (T1) и холодного (T2) контактов. В небольшом интервале температур термоэдс E можно считать пропорциональной разности температур: E = α12 (T2-T1),где α12 термоэлектрическая способность пары (или коэффициент термоэдс). В простейшем случае коэффициент термоэдс определяется только материалами проводников, однако строго говоря, он зависит и от температуры, и в некоторых случаях с изменением температуры
α12 меняет знак. Более корректное выражение для термоэдс:
Величина термоэдс составляет милливольты при разности температур в 100 К и температуре холодного спая в 0°С (например, пара медь-константан даёт 4,25 мВ, платина-платинородий — 0,643 мВ, нихром-никель — 4,1 мВ )
Читайте также:
