Виды напряжений в металлических конструкциях
Напряжения в зависимости от вида подразделяются на основные, дополнительные, местные и начальные.
Основные напряжения - напряжения, определяемые от внешних воздействий методами, излагаемыми в курсе сопротивления материалов. Основные напряжения определяются по усилиям, установленным для принятой идеализированной расчетной схемы (например, в решетчатых конструкциях - фермах и др., исходя из шарнирного вместо практически жесткого сопряжения стержней в узлах, иногда без учета пространственной. работы системы в целом и т. п.), без учета местных, дополнительных и внутренних напряжений. Искусственно создаваемые предварительные напряжения также относятся к основным.
Поскольку основные напряжения уравновешивают внешние воздействия и определяют несущую способность элементов конструкций, они и выявляются расчетом и по ним в основном судят о надежности конструкций (за исключением особых случаев).
Дополнительные напряжения - напряжения, возникающие в результате дополнительных связей по отношению к принятой идеализированной расчетной схеме (например, из-за жесткости узлов, дополнительных систем связей и т. п.). Дополнительные напряжения, определямые методами строительной механики, при пластичном материале не оказывают существенного влияния на несущую способность конструкции. Это объясняется тем, что при расчетных нагрузках материал в местах перенапряжения переходит в пластическое состояние, принаступлении которого дополнительные напряжения или уменьшаются, или снимаются. Например, из-за жесткости узлов в элементе решетчатой конструкции возникают помимо осевой силы моменты, которые вызывают Дополнительные напряжения в крайних фибрах. Повышение напряжения приводит к раннему развитию пластических деформаций в фирбах, что, в свою очередь, снижает моменты, а в пределе, при развитии пластических деформаций по всему сечению, узел свободно поворачивается. Благодаря этому предельная нагрузка получается такой же, как и при действии только одной продольной силы. Поэтому дополнительные напряжения не учитываются расчетом (за исключением некоторых специальных случаев).
Местные напряжения могут быть двух видов:
- в результате внешних воздействий;
- в местах резкого изменения или нарушения сплошности сечения, где вследствие искажения силового потока происходит концентрация напряжений.
В первом случае местные напряжения уравновешиваются с внешними воздействиями, во втором - они внутренне уравновешены.
К местным напряжениям, возникающим из-за внешних воздействий, относятся напряжения в местах приложения сосредоточенных нагрузок - на опорах, в местах опирания каких-либо других конструкций, под катками мостовых кранов в подкрановых балках, в местах крепления вспомогательных элементов. Местные напряжения могут привести к развитию чрезмерных пластических деформаций, трещин или к потере устойчивости в тонких элементах сечений (например, стенки двутавра). Местные напряжения этого вида учитывают в расчете.
Начальные напряжения. Начальными называются напряжения, которые имеются в ненагруженном внешней нагрузкой элементе и которые появились в нем в результате неравномерного остывания после прокатки или сварки или в результате предшествующей работы элемента и его пластической деформации, поэтому они называются также внутренними, собственными или остаточными. Начальные напряжения всегда уравновешены, поэтому эпюры их двузначны, а, эпюра).
Виды напряжений в металлических конструкциях
Основные напряжения - напряжения, определяемые от внешних воздействий методами, излагаемыми в курсе сопротивления материалов. Основные напряжения определяются по усилиям, установленным для принятой идеализированной расчетной схемы (например, в решетчатых конструкциях - фермах и др., исходя из шарнирного вместо практически жесткого сопряжения стержней в узлах, иногда без учета пространственной. работы системы в целом и т. п.), без учета местных, дополнительных и внутренних напряжений. Искусственно создаваемые предварительные напряжения также относятся к основным.
Дополнительные напряжения - напряжения, возникающие в результате дополнительных связей по отношению к принятой идеализированной расчетной схеме- (например, из-за жесткости узлов, дополнительных систем связей и т. п.). Дополнительные напряжения, определямые методами строительной механики, при пластичном материале не оказывают существенного влияния на несущую способность конструкции. Это объясняется тем, что при расчетных нагрузках материал в местах перенапряжения переходит в пластическое состояние, принаступлении которого дополнительные напряжения или уменьшаются, или снимаются. Например, из-за жесткости узлов в элементе решетчатой конструкции возникают помимо осевой силы моменты, которые вызывают Дополнительные напряжения в крайних фибрах. Повышение напряжения приводит к раннему развитию пластических деформаций в фирбах, что, в свою очередь, снижает моменты, а в пределе, при развитии пластических деформаций по всему сечению, узел свободно поворачивается. Благодаря этому предельная нагрузка получается такой же, как и при действии только одной продольной силы. Поэтому дополнительные напряжения не учитываются расчетом (за исключением некоторых специальных случаев).
- в результате внешних воздействий; - в местах резкого изменения или нарушения сплошности сечения, где вследствие искажения силового потока происходит концентрация напряжений.
Начальные напряжения. Начальными называются напряжения, которые имеются в ненагруженном внешней нагрузкой элементе и которые появились в нем в результате неравномерного остывания после прокатки или сварки или в результате предшествующей работы элемента и его пластической деформации, поэтому они называются также внутренними, собственными или остаточными. Начальные напряжения всегда уравновешены, поэтому эпюры их двузначны, а, эпюра /).
2. Условие пластичности. Учет развития пластических деформаций при расчете конструкций
Известно, что у стали при . после упругой работы и небольшого переходного участка наступает пластическое течение, что на диаграмме отмечается протяженной площадкой текучести. При работе конструкций из стали в упругопластической области в ЦЕЛЯХ упрощения расчетных предпосылок диаграмму работы стали без большой погрешности и в сторону некоторого запаса можно уподобить работе идеального упрогопластического тела, которое совершенно упруго до предела текучести и совершенно пластично после него (рис. 3.10 - диаграмма Прандтля)
В этом предположении переход в пластическую стадию при одноосном напряженном состоянии (простом растяжении или сжатии) происходит при достижении нормальным напряжением предела текучести. При многоосном напряженном состоянии переход в пластическую стадию зависит не от одного напряжения, а от функции напряжений, характеризующей так называемое условие пластичности (условие перехода в пластическое состояние). Условие пластичности записывается в зависимости от теории прочности, которая кладется в основу расчета. К работе стали и алюминиевых сплавов наиболее близки III и IV теории прочности. В СНиП П-23-81 для расчетов металлических конструкций принята IV энергетическая теория прочности.
По этой теории пластичность наступает тогда, когда потенциальная энергии (работа) изменения формы тела достигает наибольшей величины.
Из курса сопротивления материалов известно, что на основе IV теории прочности одноосное приведенное напряжение, эквивалентное по переходу материала в пластическое состояние данному сложному напряженному состоянию, определяется в главных напряжениях по формуле:
Приведенное напряжение может быть выражено в нормальных и касательных напряжениях:
Отсюда при изгибе (вдали от точек приложения нагрузки):
По III теории прочности:
3. Предельные состояния и расчет стержней, сжатых осевой силой
Предельные состояния сжатых жестких стержней определяются развитием пластических деформаций при достижении напряжениями предела текучести, а гибких стержней - потерей устойчивости.
Расчет на прочность. Расчет на прочность центрально сжатых элементов выполняется так же, как и центрально растянутых. Вместе с тем в этом случае могут быть учтены некоторые отличительные особенности работы материала на сжатие. Например, проверка прочности элементов с соединениями на болтах повышенной прочности может быть выполнена по сечению "брутто", т. е. без учета ослабления сечения отверстиями.
При малой длине выступающей части сжатого элемента (например, опорное ребро балки) его сечение определяется расчетом на местное смятие торцевой поверхности (при наличии пригонки) по формуле (3.16) с заменой в ней расчетного сопротивления R на Rсм.т=Rв.
Проверка устойчивости гибких стержней, сжатых осевой силой. Из курса сопротивления материалов известно, что при равенстве работы, совершаемой внешними силами при сближении концов стержня, работе деформации изгиба сжимаемого стержня сжимающая сила достигает своего критического значения. Прямой стержень при нагрузке его осевой силой до критического состояния имеет прямолинейную форму устойчивого состояния. При достижении силой критического значения его прямолинейная форма перестает быть устойчивой, стержень изгибается в плоскости, меньшей жесткости, и устойчивым состоянием у него будет новая криволинейная форма. Но уже при незначительном увеличении нагрузки искривление стержня начинает быстро нарастать и стержень теряет несущую способность.
Для упругого стержня, сжатого осевой силой шарнирно закрепленного по концам (основной случай), критическую силу определяют по формуле, выведенной в 1744 г. Л. Эйлером:
Соответственно критические напряжения:
где - площадь поперечного сечения без учета ослабления отверстиями для заклепок и болтов;
- гибкость стержня, равная отношению расчетной длины стержня к радиусу инерции его сечения;
- расчетная длина стержня; - коэффициент приведения полной длины стержня L к расчетной, принимаемые в зависимости от условий закрепления стержня и его нагруження.
При средних и малых гибкостях стержня (потеря его устойчивости происходит в упругопластической стадии заботы материала при ). Пока стержень сохраняет прямолинейную форму, напряжения распределяются равномерно по сечению (напряжения - ). При отклонении стержня от прямолинейного состояния на эти напряжения накладываются напряжения изгиба. Со стороны дополнительного сжатия от изгиба материал работает в угругопластическо стадии, со стороны растягивающих напряжений от изгиба материал работает упруго (разгрузка происходит по закону Гука)
Таким образом, часть сечения 1 работает в упругой стадии с модулем деформаций Е, часть сечения 2-в упругопластичесчой стадии с модулем деформации .
Эпюра приращений внутренних напряжений является самоуравновешенной. Поскольку, нейтральная ось изгиба вмещается в сторону растягивающих напряжений, и внешний момент получает приращение . Приращение момента внутреннних капряжений от изгиба .
В критическом состоянии приращение момента внешних сил равно приращению момента внутренних напряжений. Из этох условия можно определить величину критической силы при работе материала в упруго-пластической стадии.
Формулу Эйлера можно расширить и на этот случай работы стержня, если принять вместо постоянного модуля упругости Е переменный приведенный модуль
момент инерции упругой части сечения 1; момент инерции упругопластической части сечения 2; общий момент инерции.
Тогда формула (3.34) запишется в виде:
4. Предельные состояния и расчет внецентренно растянутых и внецентренно сжатых элементов
Предельные состояния внецентренно растянутых и жестких внецентренно сжатых элементов определяются несущей способностью по прочности или развитием пластических деформаций, а гибких внецентренно сжатых - потерей устойчивости.
Расчет на прочность. Предельные состояния по прочности внецентренно растянутых (растянуто-изогнутых) и внецентренно сжатых (сжато-изогнутых) элементов конструкций при динамических воздействиях, а также элементов конструкций, выполненных из сталей высокой прочности с расчетным сопротивлением R >580 МПа, определяются достижением наибольшими фибровыми напряжениями расчетного сопротивления. Их расчет выполняется по упругой стадии работы материала по формуле:
Для внецентренно сжатых и внецентренно растянутых элементов из пластичных сталей с пределом текучести до 580 МПа при действии статических нагрузок предельное состояние по прочности определяется с учетом развития пластических деформаций.
Развитие пластических деформаций при наличии момента и продольной силы так же, как и в изгибаемых элементах, приводит к образованию шарнира пластичности, но при этом положение нейтральной оси в процессе развития пластических деформаций смещается (рис. 3.17) . При увеличении момента и продольной силы на одной из сторон стержня фибровые напряжения достигают предела текучести и затем останавливаются в своем развитии.
Напряжения в прочих фибрах (угол наклонной части эпюры напряжений) продолжают расти, пока, наконец, напряжения на другой стороне стержня не достигнут предела текучести, после чего пластичность распространяется на все фибры сечения (см. рис. 3.17) . Очевидно, что разность площадей эпюр напряжений, умноженная на , равна предельной продольной силе
где A1 и A2 - площади частей сечения, показанные на рис. 3.17 .
Площадь определяет одну составляющую пары изгибающего момента; такая же площадь на другой стороне сечения должна определять вторую составляющую этой пары. Отсюда предельный момент
где е - расстояние между центрами площадей A1.
Таким образом, в пластической стадии напряжения от продольной силы и момента можно условно разделить. Напряжения от продольной силы занимают среднюю часть - сечения A1= A-2A2, а напряжения от момента края на площадях A2.
При развитии шарнира пластичности соотношение предельных продольных сил, отвечающих наличию момента N м пр и его отсутствию N 0 пропределяется отношением , а соотношение предельных моментов, отвечающих наличию продольной силы M n пр и ее отсутствию M 0 пр, определяется отношением .
Для прямоугольного сечения связь между этими отношениями выражается параболой (рис. 3.18) .
Для двутавровых сечений эта зависимость ближе к линейной и может быть выражена:
где а - коэффициент, определяемый характером распределения материала по сечению двутавра.
Аналогичный подход может быть использован и при работе стержня на совместное действие двух моментов Мх и Му и нормальной силы.
Образование шарнира пластичности приводит к неограниченному росту перемещений. Для обеспечения эксплуатационной пригодности конструкций проверяют прочность элементов при совместном действии изгиба и осевой силы, как и изгибаемых элементов, по критерию ограниченных пластических деформаций
Коэффициенты п, сх и су учитывают степень развития пластических деформаций и зависят от формы сечения. Численные значения этих коэффициентов при 8=3 для некоторых типов сечения приведены в прил. 5.
Проверка устойчивости внецентренно сжатых (сжато-изгибаемых) элементов. При приложении сжимающей силы с эксцентрицитетом стержень работает как внецентренно сжатый. При одновременном приложении продольной осевой силы и поперечной нагрузки, вызывающей изгиб, стержень будет сжато-изгибаемым. Хотя в том и в другом случае по сечению развиваются напряжения одинакового вида, вызванные продольной силой и моментом, работа стержня в этих случаях несколько отличается главным образом в предельном состоянии при малых гиб-костях. Однако в целях упрощения практических методов расчета (в небольшой запас) сжато-изгибаемые стержни при рассмотрении критического состояния потери устойчивости приравниваются к внецентренно сжатым, имеющим эксцентрицитет .
5. Проверка местной устойчивости элементов
У тонкостенных стержней, особенно небольшой гибкости, стенка или полка могут потерять устойчивость раньше, чем происходит потеря устойчивости стержня в целом. Потеря устойчивости каким-либо элементом сечения стержня (местная потеря устойчивости) и выход его из работы (даже частичный) резко ослабляют стержень, часто делая недеформированную, часть сечения несимметричной; центр изгиба при этом перемещается, стержень начинает закручиваться и быстро теряет устойчивость.
Потеря устойчивости может произойти от воздействия нормальных, равномерно распределенных по сечению напряжений (стенки и полки центрально сжатых и полки изгибаемых элементов), нормальных неравномерно распределенных напряжений (стенки внецентренно сжатых стержней и изгибаемых элементов), касательных напряжений (стенки изгибаемых элементов) и от совместного воздействия нормальных и касательных напряжений.
Потеря устойчивости может происходить как при упругой, так и при упругопластической работе элемента.
При решении задачи о местной устойчивости считают, что отдельные элементы, составляющие стержень, работают как пластинки, сочлененные между собой шарнирно, упруго или жестко.
Критическую силу потери устойчивости находят из условия равенства работы внешних сил и напряжений, возникающих в пластине при данной форме деформации. Критическая сила зависит от упругих свойств материала, размеров пластины - ширины, длины (расстояния между окаймлениями пластины), толщины и условий закрепления ее по краям. Длинная пластинка, закрепленная только по продольным краям, теряет устойчивость по волнообразной поверхности. Длина волны зависит от силовых воздействий и характера закрепления пластины, в частности при равномерном распределении напряжений длина волны равна ширине пластины. При большом числе волн критическая сила потери местной устойчивости при упругой работе материала:
Соответственно критическое напряжение:
Для того чтобы местная устойчивость не ограничивала несущей способности элемента, действующие в пластинке напряжения не должны превышать сигма. Варьируя размерами пластинки и условиями закрепления, добиваются повышения сигма и обеспечения местной устойчивости.
Рассмотрим наиболее распространенные случаи местной устойчивости элементов металлических конструкций
Пояса балок и колонн
Сжатые пояса двутавровых сечений балок и колонн представляют собой длинную пластину, нагруженную равномерно распределенными по сечению пластины нормальными напряжениями, действующими вдоль ее длинной стороны, и прикрепленную длинной стороной к стенке двутаврового сечения. Потеря устойчивости такой пластины происходит путем волнообразного выпучивания ее краев, середина же пластины остается прямолинейной, так как стенка препятствует ее выпучиванию.
В балках, работающих без учета пластических деформаций, критические напряжения, полученные по формуле (3.69), приравниваются к расчетному сопротивлению материала пояса сигмакр = R и из этого условия получается, что неокаймленный свес пояса (половина ширины пояса) должен быть:
Для малоуглеродистых сталей отношение свеса к толщине пояса составляет около 15.
В случае учета пластических деформаций в работе балки устойчивость пояса ухудшается, и требования для проверки устойчивости поясов двутавровых балок получены из условия одновременной потери устойчивости стенки и пояса.
В колоннах местная устойчивость поясных листов приравнивается к общей устойчивости колонны и принимается сигмаКР =R. Уменьшение сигмаКР для полок колонн дает возможность увеличить свес пояса, и поэтому в колоннах свес пояса обычно может быть больше, чем в балках. Неокаймленный свес полки колонны определяется по формуле:
Стенки центрально сжатых колонн двутаврового сечения представляют собой длинную пластину, нагруженную равномерно распределенными по сечению пластины нормальными напряжениями, действующими вдоль ее длинной стороны. Эта пластина прикреплена к поясам колонн, которые препятствуют ее выпучиванию по краям. Потеря устойчивости такой пластины может происходить путем волнообразного выпучивания ее середины, причем длина полуволны составляет около 0,7 ширины пластины. Коэффициент с в формуле (3.69) зависит от условий закрепления поясов и стенки центрально-сжатых колонн.
Устойчивость стенки колонн подобно устойчивости поясов приравнивается к общей устойчивости колонны, но предельные отношения ширины стенки к ее толщине благодаря разным условиям закрепления пластины получаются больше, и для стенок из малоуглеродистой стали доходят до 70:
Стенки балок двутаврового сечения представляют собой пластины, упруго защемленные в поясах, часто дополнительно укрепленные поперечными и продольными ребрами жесткости. Они могут испытывать нормальные, касательные и местные напряжения
Напряжения в стальных профилях
Напряжения в стальных конструкциях подразделяются на основные, дополнительные, местные и начальные.
1. Основные напряжения определяются от внешних нагрузок для упругой стадии работы. Эти напряжения уравновешивают усилия в элементах от внешних воздействий и определяются по формулам:
По ним ведется расчет элементов конструкций. Например, для ферм идеализированной является схема 1 (рисунок 4.1.1) с шарнирными соединениями в узлах. В действительности шарниров там нет, узлы ферм всегда конструктивно выполняются жесткими (схема 2). В легких фермах изгибная жесткость элементов фермы невелика, ею часто пренебрегают и определяют усилия так же, как в шарнирной системе.
2. Если строго следовать реальной расчетной схеме (рисунок 4.1.1, схема 2), то ферму следует рассчитать как много раз статически неопределимую систему, найти моменты в элементах, в узлах и учесть их в расчете. К основным напряжениям в этом случае добавятся напряжения от моментов, которые называются дополнительными. В легких фермах ими пренебрегают, так как они выравниваются за счет пластической работы материала. Однако сокращение пластических деформаций в высокопрочных сталях, увеличение изгибной жесткости элементов в тяжелых фермах, снижение коэффициентов запаса, а также возможность применения современной вычислительной техники – все это приводит к необходимости учета дополнительных напряжений в расчетах как основных.
Рисунок 4.1.1 – Расчетные схемы ферм: 1 – идеализированная; 2 – реальная
Причиной появления дополнительных напряжений могут быть и другие, обычно не учитываемые в расчетах связи.
3.Местные, или локальные, напряжения возникают в местах: 1) изменения сечения элементов, 2) приложения на небольшой длине больших сосредоточенных нагрузок. Действуя на небольшой длине, они не сказываются на общих деформациях конструкций. Они приводят к появлению плоского напряженного состояния. Это увеличивает опасность разрушения конструкций.
Рисунок 4.1.2 — Эпюры напряжений от ослабления сечения круглым отверстием
Местные напряжения первого рода – концентрация напряжений – приводят к искажению силового потока, являются внутренне уравновешенными и быстро уменьшаются по мере удаления от концентратора (рис. 5). Величина локальных (пиковых) напряжений зависит от того, как резко меняется сечение в месте его изменения и характеризуется коэффициентом концентрации напряжений
где максимальное (пиковое) напряжение в месте концентрации; среднее напряжение, подсчитанное по ослабленному сечению.
Теоретически напряжение по краю трещины при упругой работе материала стремится к бесконечности, реально доходит до 9. За счет пластичности материала напряжения быстро выравниваются. Напряжение при нормальной температуре и статической нагрузке на несущую способность заметно не сказывается и в расчетах не учитывается. Однако при пониженных температурах и при динамических, циклических нагрузках может быть причиной хрупкого разрушения. Мероприятия по предотвращению этого – подбор стали в соответствии с условиями работы и снижение концентрации напряжений плавным изменением сечения.
Рисунок 4.1.3 – Местные напряжения от сосредоточенной нагрузки
Местные напряжения второго рода уравновешивают внешние воздействия. Могут привести к плоскому напряженному состоянию – сжатию или растяжению в двух направлениях и, как следствие, – трещине или потере местной устойчивости в тонких элементах. Местные напряжения этого вида учитываются в расчетах, возможно также местное усиление конструкций (ребра жесткости, увеличение толщины элементов и т.п.)
4.Начальные напряжения, имеющиеся в элементах стальных конструкций до их загружения, связаны, как правило, с нагреванием металла при изготовлении проката или сварке и неравномерным его остыванием. Например, в прокатных двутаврах полки всегда значительно толще стенки, поэтому они остывают значительно медленнее ее. Поэтому последняя раньше переходит через температуру 500¸600 о С и в ней появляется модуль упругости Е > 0, тогда как в рядом расположенных полках Е = 0, и они способны пластически деформироваться без появления в них каких-либо напряжений. Позже полки также переходят через этот интервал и, остывая дальше, будут, работая вместе со стенкой, натягиваться, опираясь на стенку и сжимая ее при этом.
Начальные напряжения самоуравновешиваются в конструкциях. Cкладываясь с основными, они могут ускорять или замедлять переход в пластическую стадию работы отдельных частей сечения, увеличивать деформации и через них влиять на устойчивость, но на несущую способность влияют слабо. Образуя плоское или объемное напряженное состояние, начальные напряжения могут способствовать хрупкому разрушению. Борьба с начальными напряжениями ведется технологическими мерами – уменьшением разности температур между отдельными частями конструкций при остывании.
Рисунок 4.1.4 – Начальные напряжения в двутавре
Иногда начальные напряжения создаются искусственно в процессе изготовления или монтажа конструкций для повышения их эффективности – в этом случае их называют предварительными и учитывают в расчетах как основные.
Допускаемые напряжения
и механические свойства материалов
Для определения допускаемых напряжений в машиностроении применяют следующие основные методы.
1. Дифференцированный запас прочности находят как произведение ряда частных коэффициентов, учитывающих надежность материала, степень ответственности детали, точность расчетных формул и действующие силы и другие факторы, определяющие условия работы деталей.
2. Табличный — допускаемые напряжения принимают по нормам, систематизированным в виде таблиц
(табл. 1 — 7). Этот метод менее точен, но наиболее прост и удобен для практического пользования при проектировочных и проверочных прочностных расчетах.
В работе конструкторских бюро и при расчетах деталей машин применяются как дифференцированный, так и. табличный методы, а также их комбинация. В табл. 4 — 6 приведены допускаемые напряжения для нетиповых литых деталей, на которые не разработаны специальные методы расчета и соответствующие им допускаемые напряжения. Типовые детали (например, зубчатые и червячные колеса, шкивы) следует рассчитывать по методикам, приводимым в соответствующем разделе справочника или специальной литературе.
Приведенные допускаемые напряжения предназначены для приближенных расчетов только на основные нагрузки. Для более точных расчетов с учетом дополнительных нагрузок (например, динамических) табличные значения следует увеличивать на 20 — 30 %.
Допускаемые напряжения даны без учета концентрации напряжений и размеров детали, вычислены для стальных гладких полированных образцов диаметром 6-12 мм и для необработанных круглых чугунных отливок диаметром 30 мм. При определении наибольших напряжений в рассчитываемой детали нужно номинальные напряжения σном и τном умножать на коэффициент концентрации kσ или kτ:
1. Допускаемые напряжения*
для углеродистых сталей обыкновенного качества в горячекатаном состоянии
* Горский А.И.. Иванов-Емин Е. Б.. Кареновский А. И. Определение допускаемых напряжений при расчетах на прочность. НИИмаш, М., 1974.
** Римскими цифрами обозначен вид нагрузки: I — статическая; II — переменная, действующая от нуля до максимума, от максимума до нуля (пульсирующая); III — знакопеременная (симметричная).
2. Механические свойства и допускаемые напряжения
углеродистых качественных конструкционных сталей
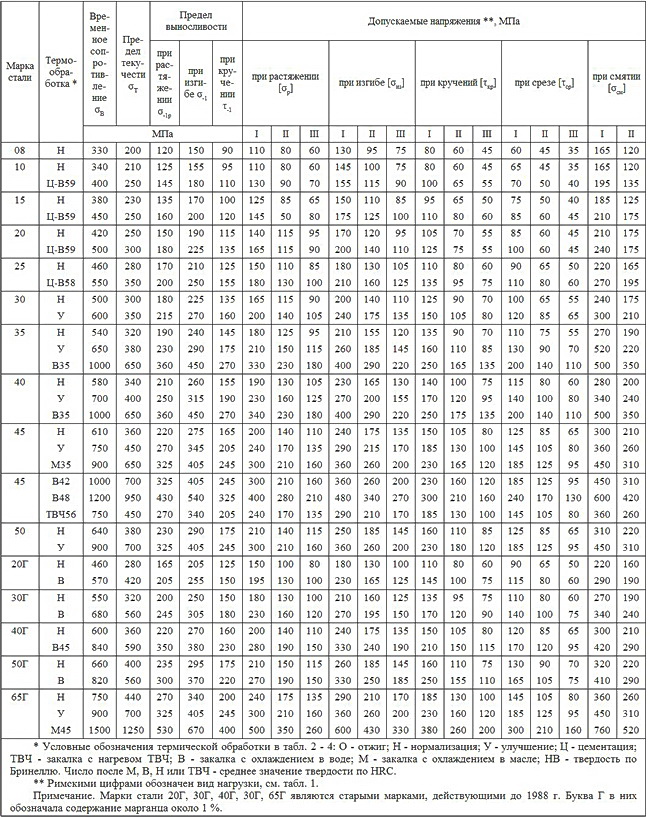
3. Механические свойства и допускаемые напряжения
легированных конструкционных сталей
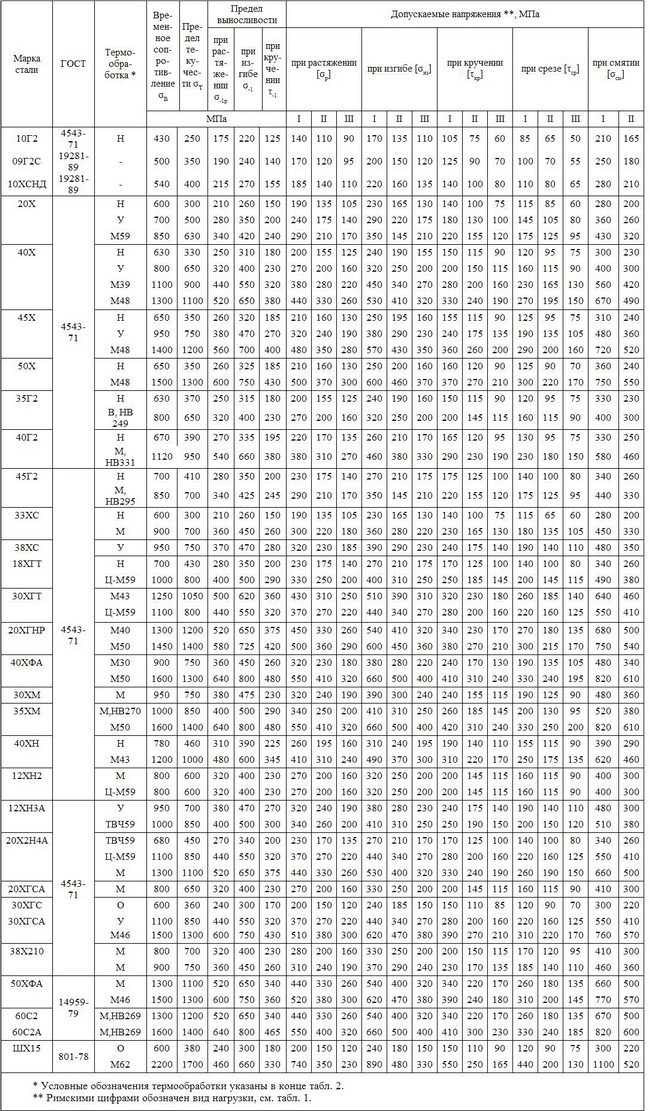
4. Механические свойства и допускаемые напряжения
для отливок из углеродистых и легированных сталей
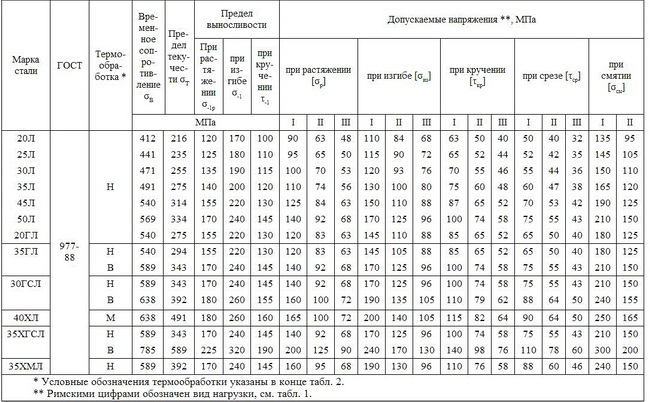
5. Механические свойства и допускаемые напряжения
для отливок из серого чугуна
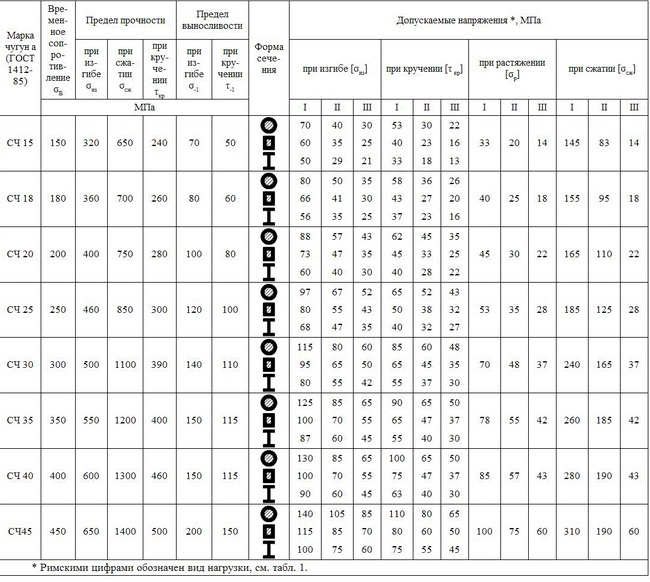
6. Механические свойства и допускаемые напряжения
для отливок из ковкого чугуна
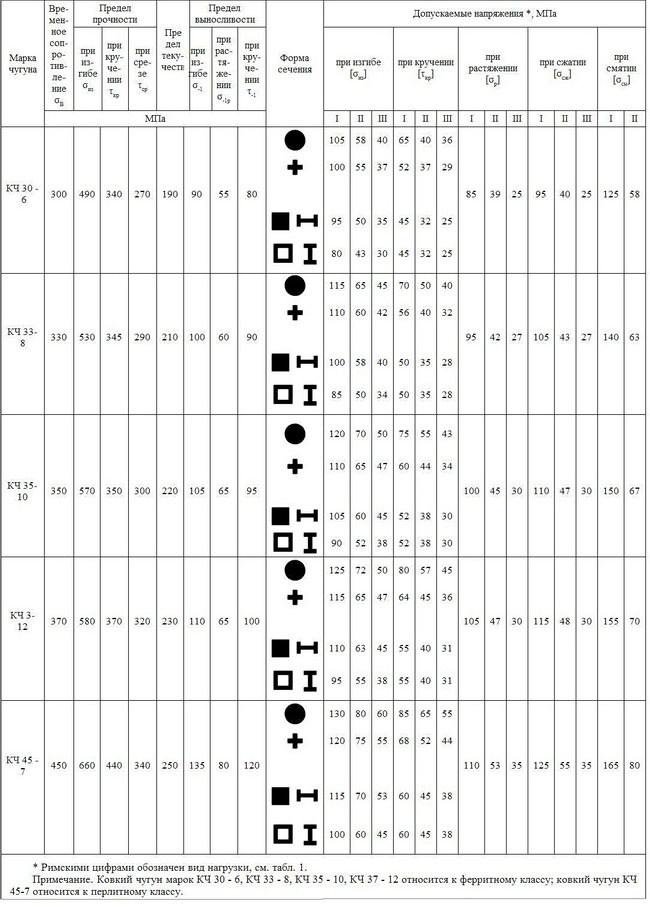
7. Допускаемые напряжения для пластмассовых деталей
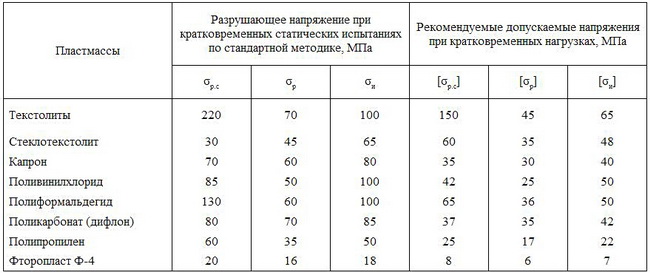
Для пластичных (незакаленных) сталей при статических напряжениях (I вид нагрузки) коэффициент концентрации не учитывают. Для однородных сталей (σв > 1300 МПа, а также в случае работы их при низких температурах) коэффициент концентрации, при наличии концентрации напряжения, вводят в расчет и при нагрузках I вида (k > 1). Для пластичных сталей при действии переменных нагрузок и при наличии концентрации напряжений эти напряжения необходимо учитывать.
Для чугунов в большинстве случаев коэффициент концентрации напряжений приближенно принимают равным единице при всех видах нагрузок (I — III). При расчетах на прочность для учета размеров детали приведенные табличные допускаемые напряжения для литых деталей следует умножать на коэффициент масштабного фактора, равный 1,4 . 5.
Приближенные эмпирические зависимости пределов выносливости для случаев нагружения с симметричным циклом:
Механические свойства и допускаемые напряжения антифрикционного чугуна:
— предел прочности при изгибе 250 ÷ 300 МПа,
— допускаемые напряжения при изгибе: 95 МПа для I; 70 МПа — II: 45 МПа — III, где I. II, III — обозначения видов нагрузки, см. табл. 1.
Ориентировочные допускаемые напряжения для цветных металлов на растяжение и сжатие. МПа:
— 30. 110 — для меди;
— 60. 130 — латуни;
— 50. 110 — бронзы;
— 25. 70 — алюминия;
— 70. 140 — дюралюминия.
Стали: допускаемые напряжения и механические свойства материалов
Допускаемые напряжения принимаем по нормам, систематизированных в виде таблиц, что удобнее для практического применения при проектировочных и проверочных прочностных расчетов.
Примечание. Условные обозначения термической обработки:
О — отжиг; Н — нормализация; У — улучшение; Ц — цементация; ТВЧ — закалка с нагревом т.в.ч.; В — закалка с охлаждением в воде; М — закалка с охлаждением в масле; НВ — твердость по Бринеллю. Число после М, В, Н или ТВЧ — среднее значение твердости по HRC.
*) Римскими цифрами обозначен вид нагрузки (см. таблицу 1): I — статическая; II — переменная, действующая от нуля до максимума и от максимума до нуля (пульсирующая), III — знакопеременная (симметричная).
Допускаемые напряжения для углеродистых сталей обыкновенного качества в горячекатаном состоянии
Механические свойства и допустимые напряжения углеродистых качественных конструкционных сталей
Примечание:
Марки стали 20Г; 30Г; 40Г; 50Г; 65Г — старые марки стали, действующие до 1988 г. Буква Г в них обозначала содержание марганца около 1 %.
Виды напряжений и их учет при расчете элементов конструкций. Основные, дополнительные, местные, начальные напряжения.
Действительное напряженное состояние даже в простейших конструкциях довольно сложно. Напряжения в зависимости от вида подразделяются на основные, дополнительные,местные и начальные.
Основные напряжения – это напряжения, развивающееся внутри элемента конструкции в результате уравновешивания воздействия внешних нагрузок. Они определяются расчетом по усилиям, установлены для принятой идеализированной расчетной схемы без учета местных, дополнительных и внутренних напряжений. Искусственно создаваемые предварительные напряжения также относятся к основным.
Дополнительныенапряжения – напряжения возникающие в результате дополнительных связей по отношению к принятой идеализированной схеме (например, защемление элементов в узлах ферм). Эти напряжения не влияют на равновесие системы в целом и в конструкциях из пластических материалов большей частью расчетом не учитываются.
К местным напряжениям относятся напряжения в местах приложения сосредоточенных нагрузок, в местах опирания других конструкций, под катками мостовых кранов в подкрановых балках, в местах крепления вспомогательных элементов. В местах с резким изменением сечения, наличием отверстий, трещин возникает местная концентрация напряжений. Концентрация напряжений при нормальной температуре и статических воздействиях расчетом не учитывается. При пониженных температурах и особенно при воздействии динамических нагрузок концентрация напряжений учитывается расчетом.Начальными (внутренними) напряжениями называются напряжения, которые имеются в ненагруженном внешней нагрузкой элементе и которые появились в нем в результате неравномерного остывания после прокатки и сварки или в результате предшествующей работы элемента и его пластической деформации. Начальные (внутренние) напряжения не оказывают влияния на прочность элемента, поскольку результирующие напряжения выравниваются при развитии пластических деформаций. Начальные напряжения в пластичных строительных сталях при расчетах не учитываются.
Работа и расчет на прочность центрально растянутых и центрально сжатых элементов.
Связь между напряжением и удлинением образца на начальном этапе испытания следует закону Гука
sГеометрически модуль упругости представляет собой .
Линейная связь между напряжением и удлинением сохраняется до величины напряжений примерно 20 кН/см 2 и со ответствует пределу пропорциональностиsр. Несколько выше этой точки лежит предел упругостиsе, соответствующий такой деформации, которая практически полностью исчезает после разгрузки образца. Предел упругости ограничивает область упругой работы материала. При дальнейшей нагрузке образца модуль упругости стали уменьшается (криволинейная часть диаграммы) и при напряжении около 24 кН/см 2 становится равным нулю (начало горизонтального участка диаграммы). Это напряжение называется пределом текучестиsу. В дальнейшем образец продолжает удлиняться без приложения дополнительной нагрузки, т. е. как бы «течет».
Область работы материала между напряжениями sе и sу является областью упругопластической работы. Горизонтальный участок диаграммы называется площадкой текучести. При относительном удлинении образца около 2,5% «течение» заканчивается и материал становится снова несущеспособным, он как бы самоупрочняется (область самоупрочнения).
При дальнейшем увеличении нагрузки удлинения продолжают нарастать, в образце образовывается шейка (местное сужение) и при относительном удлинении 20— 25% происходит разрыв.
Наибольшее условное напряжение, достигнутое в образце (точка Run=40 кН/см 2 для малоуглеродистых сталей), называется временным сопротивлением (пределом прочности) стали. Сталь при работе на сжатие в коротких элементах ведет себя так же, как и при растяжении. Значение предела текучести sу, модуля упругости Е и величина площадки текучести равны аналогичным показателям при растяжении. При расчете коротких элементов, которые не
Диаграмма работы малоуглеродистой стали при растяжении.
s
могут потерять устойчивость, расчетное сопротивление принимается более высоким чем, при растяжении и сжатии. Иная картина наблюдается в длинных сжатых элементах, длина которых в несколько раз превышает ширину поперечного сечения (гибкие элементы). В этом случае элемент может потерять свою несущую способность, т. е. способность сопротивляться внешним воздействиям, не в результате разрушения материала, а в результате потери устойчивости (продольного изгиба).
В соответствии с неравенством первой группы предельных состояний, прочность сечения будет обеспечена, если
- продольная сила в стержне от расчетных нагрузок;
An - площадь поперечного сечения нетто;
R - расчетное сопротивление, принимаемое равным:
- Ry - если развитие пластических деформаций не допускается;
- Ry или - коэффициент надежности по материалу при расчете конструкций по временному сопротивлению.
Проверка по II ГПС сводиться к ограничению удлинений (укорочений) стержня от нормативных нагрузок:
- расчетная длина стержня;
А – площадь поперечного сечения стержня брутто.
N – продольная сила в стержне от нормативных нагрузок.
© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.007)
Виды напряжений в стальных конструкциях
Виды напряжений и их учет в расчете элементов стальных конструкций
Основные напряжения — напряжения, определяемые от внешних воздействий методами, излагаемыми в курсе сопротивления материалов. Основные напряжения определяются по усилиям, установленным для принятой идеализированной расчетной схемы (например, в решетчатых конструкциях—фермах и др., исходя из шарнирного вместо практически жесткого сопряжения стержней в узлах, иногда без учета пространственной работы системы в целом и т. п.), без учета местных, дополнительных и внутренних напряжений.
Поскольку основные напряжения уравновешивают внешние воздействия и определяют несущую способность элементов конструкций, они и выявляются расчетом и по ним в основном судят о надежности конструкций.
Дополнительные напряжения— напряжения, возникающие в результате дополнительных связей по отношению к принятой идеализированной расчетной схеме (например, из-за жесткости узлов, дополнительных систем связей и т. п.). Дополнительные напряжения, определимые методами строительной механики, при пластичном материале не оказывают существенного влияния на несущую способность конструкции.
Местные напряжениямогут быть двух видов:
1. в результате внешних воздействий;
2. в местах резкого изменения или нарушения сплошности сечения, где вследствие искажения силового потока происходит концентрация напряжений.
В первом случае местные напряжения уравновешиваются с внешними воздействиями, во втором — они внутренне уравновешены.
К местным напряжениям, возникающим из-за внешних воздействий, относятся напряжения в местах приложения сосредоточенных нагрузок — на опорах, в местах опирания каких-либо других конструкций (рис. а),под катками мостовых кранов в подкрановых балках (рис. б), в местах крепления вспомогательных элементов. Местные напряжения могут привести к развитию чрезмерных пластических деформаций, трещин или к потере устойчивости в тонких элементах сечений (например, стенки двутавра).
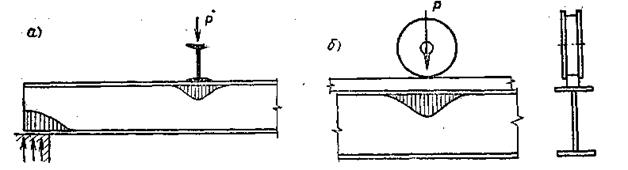
а — в местах приложения сосредоточенных нагрузок; б — под катком крана
Начальные напряжения. Начальными называются напряжения, которые имеются в ненагруженном внешней нагрузкой элементе и которые появились в нем в результате неравномерного остывания после прокатки или сварки или в результате предшествующей работы элемента и его пластической деформации, поэтому они называются также внутренними, собственными или остаточными. Начальные напряжения всегда уравно-вешены, поэтому эпюры их двузначны.
Начальные напряжения, складываясь с напряжениями, вызванными внешней нагрузкой, приводят к тому, что результирующие напряжения в материале существенно отличаются от напряжений, определяемых расчетом. При неблагоприятном распределении напряжений (например, при результирующем поле, плоскостном или объемном с нормальными напряжениями одного знака) развитие пластических деформаций может оказаться затрудненным, в результате чего появится опасность хрупкого разрушения. Начальные напряжения приводят к повышению деформации, как бы снижая модуль упругости элемента, что может сказаться неблагоприятно на устойчивости при продольном изгибе. Борьба с начальными напряжениями ведется преимущественно конструктивными мероприятиями и соответствующим ведением технологического процесса при изготовлении металлических конструкций (при сварке и т. п.).
Предварительное напряжение, создаваемое в конструкциях с целью повышения ее эффективности, также является начальным напряжением.
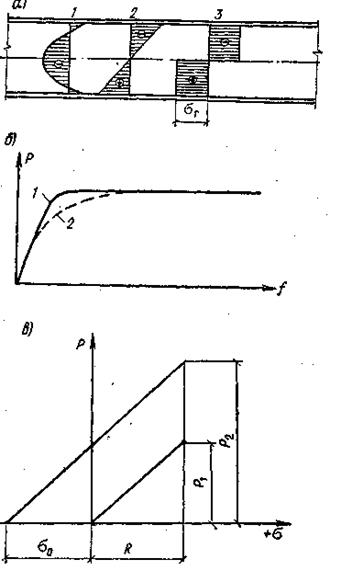
а — напряжения в балке двутаврового сечения (1 — начальные напряжения; 2 — напряжения от внешней нагрузки; 3 — суммарные напряжения при образовании шарнира пластичности); б — прогибы балки (1 — при отсутствии начальных напряжений; 2 — при наличии начальных напряжений); в — повышение несущей способности балок созданием предварительного напряжения; σо — предварительное напряжение; R — расчетное сопротивление; Р1 — максимальная нагрузка без предварительного напряжения; Р2 — то же, с предварительным напряжением
Создавая предварительное напряжение, можно повысить несущую способность и жесткость конструкции, уменьшить перемещения, повысить усталостную прочность.
— продольная сила в стержне от расчетных нагрузок;
An — площадь поперечного сечения нетто;
R — расчетное сопротивление, принимаемое равным:
— Ry — если развитие пластических деформаций не допускается;
— Ry или — коэффициент надежности по материалу при расчете конструкций по временному сопротивлению.
— расчетная длина стержня;
Читайте также:
