Увеличение электрического сопротивления чистых металлов с ростом температуры обусловлено
В начале XX века была создана классическая электронная теория проводимости металлов (П. Друде, 1900 г., Х.Лоренц, 1904 г.), которая дала простое и наглядное объяснение большинства электрических и тепловых свойств металлов.
Рассмотрим некоторые положения этой теории.
Свободные электроны
Металлический проводник состоит из:
1) положительно заряженных ионов, колеблющихся около положения равновесия, и
2) свободных электронов, способных перемещаться по всему объему проводника.
Таким образом, электрические свойства металлов обусловлены наличием в них свободных электронов с концентрацией порядка 10 28 м –3 , что примерно соответствует концентрации атомов. Эти электроны называются электронами проводимости. Они образуются путем отрыва от атомов металлов их валентных электронов. Такие электроны не принадлежат какому-то определенному атому и способны перемещаться по всему объему тела.
В металле в отсутствие электрического поля электроны проводимости хаотически движутся и сталкиваются, чаще всего с ионами кристаллической решетки (рис. 1). Совокупность этих электронов можно приближенно рассматривать как некий электронный газ, подчиняющийся законам идеального газа. Средняя скорость теплового движения электронов при комнатной температуре составляет примерно 10 5 м/с.
Электрический ток в металлах
Ионы кристаллической решетки металла не принимают участие в создании тока. Их перемещение при прохождении тока означало бы перенос вещества вдоль проводника, что не наблюдается. Например, в опытах Э. Рикке (1901 г.) масса и химический состав проводника не изменялся при прохождении тока в течении года.
Экспериментальное доказательство того, что ток в металлах создается свободными электронами, было дано в опытах Л.И. Мандельштама и Н. Д. Папалекси (1912 г., результаты не были опубликованы), а также Т. Стюарта и Р. Толмена (1916 г.). Они обнаружили, что при резкой остановке быстро вращающейся катушки в проводнике катушки возникает электрический ток, создаваемый отрицательно заряженными частицами — электронами.
- электрический ток в металлах — это направленное движением свободных электронов.
Так как электрический ток в металлах образуют свободные электроны, то проводимость металлических проводников называется электронной проводимостью.
Электрический ток в металлах возникает под действием внешнего электрического поля. На электроны проводимости, находящиеся в этом поле, действует электрическая сила, сообщающая им ускорение, направленное в сторону, противоположную вектору напряженности поля. В результате электроны приобретают некоторую добавочную скорость (ее называют дрейфовой). Эта скорость возрастает до тех пор, пока электрон не столкнется с атомом кристаллической решетки металла. При таких столкновениях электроны теряют свою избыточную кинетическую энергию, передавая ее ионам. Затем электроны снова разгоняются электрическим полем, снова тормозятся ионами и т.д. Средняя скорость дрейфа электронов очень мала, около 10 –4 м/с.
- Скорость распространения тока и скорость дрейфа не одно и то же. Скорость распространения тока равна скорости распространения электрического поля в пространстве, т.е. 3⋅10 8 м/с.
- При столкновении с ионами электроны проводимости передают часть кинетической энергии ионам, что приводит к увеличению энергии движения ионов кристаллической решетки, а, следовательно, и к нагреванию проводника.
Сопротивление металлов
Сопротивление металлов объясняется столкновениями электронов проводимости с ионами кристаллической решетки. При этом, очевидно, чем чаще происходят такие столкновения, т. е. чем меньше среднее время свободного пробега электрона между столкновениями τ, тем больше удельное сопротивление металла.
В свою очередь, время τ зависит от расстояния между ионами решетки, амплитуды их колебаний, характера взаимодействия электронов с ионами и скорости теплового движения электронов. С ростом температуры металла амплитуда колебаний ионов и скорость теплового движения электронов увеличиваются. Возрастает и число дефектов кристаллической решетки. Все это приводит к тому, что при увеличении температуры металла столкновения электронов с ионами будут происходить чаще, т.е. время τ уменьшается, а удельное сопротивление металла увеличивается.
См. так же
Зависимость сопротивления от температуры
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления от температуры выражается линейной функцией:
\(~\rho = \rho_0 \cdot (1 + \alpha \cdot \Delta t),\)
где Δt = t - t0, t0 = 0 °C, ρ0, ρ — удельные сопротивления вещества проводника соответственно при 0 °С и t °C, α — температурный коэффициент сопротивления, измеряемый в СИ в Кельвинах в минус первой степени (К -1 ) (или °C -1 ).
- Температурный коэффициент сопротивления вещества — это величина, численно равная относительному изменению удельного сопротивления проводника при его нагревании на 1 К:
Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. Для большинства металлов в интервале температур от 0 ° до 100 °С коэффициент α изменяется от 3,3⋅10 –3 до 6,2⋅10 –3 К –1 (таблица 1). У химически чистых металлов α = 1/273 К -1 .
- Существуют специальные сплавы, сопротивление которых практически не изменяется при нагревании, например, манганин и константан. Их температурные коэффициенты сопротивления очень малы и равны соответственно 1⋅10 –5 К –1 и 5⋅10 –5 К –1 .
Температурный коэффициент сопротивления (при t от 0 °С до 100 °C)
| Вещество | α, 10 –3 °К –1 | Вещество | α, 10 –3 °К –1 |
|---|---|---|---|
| Алюминий | 4,2 | Нихром | 0,1 |
| Вольфрам | 4,8 | Олово | 4,4 |
| Железо | 6,0 | Платина | 3,9 |
| Золото | 4,0 | Ртуть | 1,0 |
| Латунь | 0,1 | Свинец | 3,7 |
| Магний | 3,9 | Серебро | 4,1 |
| Медь | 4,3 | Сталь | 4,0 |
| Никель | 6,5 | Цинк | 4,2 |
Если пренебречь изменением размеров металлического проводника при нагревании, то такую же линейную зависимость от температуры будет иметь и его сопротивление
\(~R_t = R_0 \cdot (1 + \alpha \cdot \Delta t) ,\)
где R0, Rt — сопротивления проводника при 0 °С и t °С.
Зависимость удельного сопротивления металлических проводников ρ от температуры t изображена на рисунке 2.

Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена. Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Сверхпроводимость
В 1911 г. голландский физик Г. Камерлинг-Оннес, изучая изменение электрического сопротивления ртути при низких температурах, обнаружил, что при температуре около 4 К (т.е. при –269 °С) удельное сопротивление скачком уменьшается (рис. 3) до нуля. Это явление Г. Камерлинг-Оннес назвал сверхпроводимостью.

Г. Камерлинг-Оннес был удостоен Нобелевской премии по физике 1913 г. «за исследования свойств вещества при низких температурах».
В дальнейшем было выяснено, что более 25 химических элементов — металлов при очень низких температурах становятся сверхпроводниками. У каждого из них своя критическая температура перехода в состояние с нулевым сопротивлением. Самое низкое значение ее у вольфрама — 0,012 К, самое высокое у ниобия — 9 К.
Сверхпроводимость наблюдается не только у чистых металлов, но и у многих химических соединений и сплавов. При этом сами элементы, входящие в состав сверхпроводящего соединения, могут и не являться сверхпроводниками. Например, NiBi, Au2Bi, PdTe, PtSb и другие.
До 1986 г. были известны сверхпроводники, обладающие этим свойством при очень низких температурах — ниже –259 °С. В 1986-1987 годах были обнаружены материалы с температурой перехода в сверхпроводящее состояние около –173 °С. Это явление получило название высокотемпературной сверхпроводимости, и для его наблюдения можно использовать вместо жидкого гелия жидкий азот.
Широкому применению сверхпроводимости до недавнего времени препятствовали трудности, связанные с необходимостью охлаждения до сверхнизких температур, для чего использовался жидкий гелий. Тем не менее, несмотря на сложность оборудования, дефицитность и дороговизну гелия, с 60-х годов XX века создаются сверхпроводящие магниты без тепловых потерь в их обмотках, что сделало практически возможным получение сильных магнитных полей в сравнительно больших объемах. Именно такие магниты требуются для создания установок управляемого термоядерного синтеза с магнитным удержанием плазмы, для мощных ускорителей заряженных частиц. Сверхпроводники используются в различных измерительных приборах, прежде всего в приборах для измерения очень слабых магнитных полей с высочайшей точностью.
На основе сверхпроводящих пленок создан ряд быстродействующих логических и запоминающих элементов для счетно-решающих устройств. При космических исследованиях перспективно использование сверхпроводящих соленоидов для радиационной защиты космонавтов, стыковки кораблей, их торможения и ориентации, для плазменных ракетных двигателей.
В настоящее время созданы керамические материалы, обладающие сверхпроводимостью при более высокой температуре — свыше 100 К, то есть при температуре выше температуры кипения азота. Возможность охлаждать сверхпроводники жидким азотом, который имеет на порядок более высокую теплоту парообразования, существенно упрощает и удешевляет все криогенное оборудование, обещает огромный экономический эффект.
См. так же
- Wikipedia Сверхпроводимость
- Буздин А., Варламов А. Страсти по сверхпроводимости в конце тысячелетия //Квант. — 2000. — № 1. — С. 2-8.
- Мякишев Г.Я. Физика: Электродинамика //§2.6. Сверхпроводимость
Недостатки электронной теории проводимости
Несмотря на то, что электронной теории проводимости металлов объяснила ряд явлений, она имеет и свои недостатки.
- Из теории следовало, что удельное сопротивление должно быть пропорционально корню квадратному из температуры (\(~\rho \sim \sqrt T\)), между тем, согласно опыту, ρ ~ Т.
- Для того чтобы получить значения удельной электрической проводимости металла, полученных из опыта, приходится принимать среднюю длину свободного пробега электронов в сотни раз большей, чем период решетки металла. Иными словами, электрон должен проходит без соударений с ионами решетки сотни атомов.
- Данная теория не смогла объяснить причину сверхпроводимости.
Приведенные выше недостатки указывают на то, что классическая электронная теория, представляя электрон как материальную точку, подчиняющуюся законам классической механики, не учитывала некоторых специфических свойств самого электрона, которые еще не были известны к началу XX века. Эти свойства были установлены позднее при изучении строения атома, и в 1924 г. была создана новая, так называемая квантовая или волновая механика движения электронов.
Как зависит удельное сопротивление металлов от температуры?
Важным свойством металлов, которое также удалось объяснить с помощью описанного выше представления о природе их электрического сопротивления, является зависимость сопротивления от температуры: опыт показывает, что сопротивление металлов при повышении температуры увеличивается.
При сильном нагревании сопротивление металла увеличивается в несколько раз: так, сопротивление нити накала электрической лампы в «рабочем состоянии» более чем в 10 раз превосходит ее сопротивление при комнатной температуре.
Увеличение сопротивления металлов при повышении температуры объясняется тем, что при нагревании усиливаются тепловые колебания ионов, то есть увеличивается отклонение кристаллической решетки от идеальной периодичности. Вследствие этого увеличивается рассеяние электронных волн на нерегулярностях решетки. Это и приводит к росту электрического сопротивления при повышении температуры.
Смотрите также похожие статьи.
Учебник по Физике для 11 класса -> Электродинамика
Учебник по Физике для 11 класса -> Электродинамика
Интересное о физике -> Энциклопедия по физике
Интересное о физике -> Энциклопедия по физике
Учебник по Физике для 11 класса -> Электродинамика
Учебник по Физике для 11 класса -> Электродинамика
Интересное о физике -> Рассказы об ученых по физике
Интересное о физике -> Рассказы об ученых по физике
Интересное о физике -> Рассказы об ученых по физике
Иллюстрации по физике для 10 класса -> Динамика
Иллюстрации по физике для 10 класса -> Кинематика
Иллюстрации по физике для 10 класса -> Кинематика
Учебник по Физике для 10 класса -> Молекулярная физика и термодинамика
Учебник по Физике для 10 класса -> Механика
Учебник по Физике для 10 класса -> Механика
Учебник по Физике для 10 класса -> Механика
Учебник по Физике для 11 класса -> Электродинамика
Учебник по Физике для 11 класса -> Электродинамика
Учебник по Физике для 11 класса -> Электродинамика
Учебник по Физике для 11 класса -> Электродинамика
Интересное о физике -> Энциклопедия по физике
Интересное о физике -> Энциклопедия по физике
Интересное о физике -> Энциклопедия по физике
Интересное о физике -> Рассказы об ученых по физике
Интересное о физике -> Рассказы об ученых по физике
Интересное о физике -> Рассказы об ученых по физике
Интересное о физике -> Рассказы об ученых по физике
Интересное о физике -> Рассказы об ученых по физике
Интересное о физике -> Рассказы об ученых по физике
Интересное о физике -> Рассказы об ученых по физике
Интересное о физике -> Рассказы об ученых по физике
Интересное о физике -> Рассказы об ученых по физике
Интересное о физике -> Рассказы об ученых по физике
Интересное о физике -> Рассказы об ученых по физике
Интересное о физике -> Рассказы об ученых по физике
Иллюстрации по физике для 10 класса -> Молекулярная физика
Иллюстрации по физике для 10 класса -> Механические колебания и волны
Иллюстрации по физике для 10 класса -> Механические колебания и волны
Иллюстрации по физике для 10 класса -> Динамика
Иллюстрации по физике для 10 класса -> Динамика
Иллюстрации по физике для 10 класса -> Динамика
Иллюстрации по физике для 10 класса -> Динамика
Иллюстрации по физике для 10 класса -> Динамика
Иллюстрации по физике для 10 класса -> Кинематика
Иллюстрации по физике для 10 класса -> Кинематика
Учебник по Физике для 10 класса -> Молекулярная физика и термодинамика
Учебник по Физике для 10 класса -> Молекулярная физика и термодинамика
Учебник по Физике для 10 класса -> Молекулярная физика и термодинамика
Учебник по Физике для 10 класса -> Молекулярная физика и термодинамика
Учебник по Физике для 10 класса -> Молекулярная физика и термодинамика
Учебник по Физике для 10 класса -> Молекулярная физика и термодинамика
Учебник по Физике для 10 класса -> Молекулярная физика и термодинамика
Учебник по Физике для 10 класса -> Механика
Учебник по Физике для 10 класса -> Механика
Учебник по Физике для 10 класса -> Механика
Учебник по Физике для 10 класса -> Механика
Учебник по Физике для 10 класса -> Механика
Учебник по Физике для 10 класса -> Механика
Учебник по Физике для 10 класса -> Механика
Учебник по Физике для 10 класса -> Механика
Учебник по Физике для 10 класса -> Механика
Учебник по Физике для 11 класса -> Строение и эволюция Вселенной
Учебник по Физике для 11 класса -> Строение и эволюция Вселенной
Учебник по Физике для 11 класса -> Квантовая физика
Электродинамика
Т. Зависимость сопротивления от температуры
Зависимость сопротивления проводника от температуры
Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что
- возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
- изменяется их концентрация при нагревании проводника.
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:
\(~\rho_t = \rho_0 (1 + \alpha t) ,\) \(~R_t = R_0 (1 + \alpha t) ,\)
где ρ0, ρt — удельные сопротивления вещества проводника соответственно при 0 °С и t °C; R0, Rt — сопротивления проводника при 0 °С и t °С, α — температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К -1 ). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Температурный коэффициент сопротивления вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.
где \(~\mathcal h \alpha \mathcal i\) — среднее значение температурного коэффициента сопротивления в интервале ΔΤ.
Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. У чистых металлов α = 1/273 К -1 . У металлов концентрация свободных носителей зарядов (электронов) n = const и увеличение ρ происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.
Формулы зависимости ρ и R от температуры для электролитов аналогичны приведенным выше формулам для металлических проводников. Необходимо отметить, что эта линейная зависимость сохраняется лишь в небольшом диапазоне изменения температур, в котором α = const. При больших же интервалах изменения температур зависимость сопротивления электролитов от температуры становится нелинейной.
Графически зависимости сопротивления металлических проводников и электролитов от температуры изображены на рисунках 1, а, б.
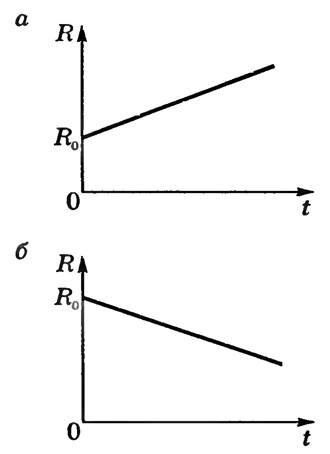
При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости. Металл переходит в сверхпроводящее состояние.
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена.
Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 256-257.
Проект по физике «Исследование зависимости электрического сопротивления проводника от температуры»
Основным законом электротехники, при помощи которого можно изучать и рассчитывать электрические цепи, является закон Ома, устанавливающий соотношение между током, напряжением и сопротивлением. Необходимо отчетливо понимать его сущность и уметь правильно пользоваться им при решении практических задач. Часто в электротехнике допускаются ошибки из-за неумения правильно применить закон Ома.
Данная исследовательская работа служит дополнением расширяющие рамки школьной программы, и посвящена закону Ома и температурному коэффициенту. Выбор темы не случаен, основным поводом послужило, что на практике при использовании ламп накаливания в цепи, при увеличение напряжения на лампе например в два раза не приводит к увеличению тока в два раза, как мы уже знаем данное условие противоречит выполняемости закона Ома. Значит -закон Ома не всегда справедлив. Хотим заметить, в школьном курсе физики данному моменту не уделено должного внимания.
В этой связи весьма важным представляется проанализировать перечисленных выше фактов и выявить решение проблемы, как методом изучения дополнительной литературы, так и рассмотреть практически. Такова цель настоящей работы.
Выявить влияние фактора температуры проводника на его электрическое сопротивление и соблюдение выполнения закона Ома от данного обстоятельства.
Объектом исследования является определяющая связь электрического напряжения с силой тока, протекающего в проводнике, и сопротивлением проводника, и его температурой.
Методы исследования:
Практическая значимость работы заключается в дополнительном представлении учащимся, что закон Ома не является фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников, но перестающим соблюдаться в ряде ситуаций.
1. Зависимость сопротивления металлических проводников от температуры.
1.1 История происхождения закона Ома
Большой в клад в формирование взаимосвязи силы тока, напряжения и сопротивление проводника внес немецкий физик Георг Симон Ом. Он руководствовался следующей идеей. Если над проводником, по которому проходит ток, подвесить на упругой нити магнитную стрелку, то угол поворота стрелки даст информацию о токе, об его изменениях при вариации элементов замкнутой цепи. Ом обратился к идее Кулона и построил крутильные весы. Магнитная стрелка оказалась точным и чувствительным гальванометром. В первых опытах, результаты которых Ом опубликовал в 1825 г., наблюдалась "потеря силы" (уменьшение угла отклонения стрелки) с увеличением длины проводника, подключенного к полюсам вольтова столба (поперечное сечение проводника было постоянным). Поскольку не было единиц измерения, пришлось выбрать эталон - "стандартную проволоку". В качестве зависимой переменной фигурировало уменьшение силы, действующей на магнитную стрелку. Опыты обнаружили закономерное уменьшение этой силы при увеличении длины проводника. Функция получила аналитическое выражение, но Ом не претендовал на установление закономерности, потому что гальванический элемент не давал постоянной ЭДС.
Большое внутренние сопротивление источника ЭДС, препятствовало исследованиям так, как сопротивление внешней цепи, которая использовались в опытах имела малые значения. Успех дальнейших экспериментов Ома решило открытие термоэлектричества. Ом использовал термопару висмут - медь; один спай помещался в лед, другой - в кипящую воду. Чувствительность "гальванометра" пришлось, естественно, увеличить. Процедура измерений заключалась в следующем. Восемь испытуемых проводников поочередно включались в цепь. В каждом случае фиксировалось отклонение магнитной стрелки. В следующей работе (1826 г.) Ом вводит понятие "электроскопической силы", пользуется понятием силы тока и записывает закон для участка цепи уже в форме, близкой к современной:
где X - сила тока, k - проводимость, w - поперечное сечение проводника, а - электроскопическая сила (электрическое напряжение на концах проводника), l - длина проводника. Несмотря на убедительные экспериментальные данные, проверка закона Ома продолжалась почти в течение всего XIX века.
1.2 Температурный коэффициент электрического сопротивления
Как мы уже знаем сопротивление проводников зависит от вещества, из которого они изготовлены, и их геометрических размеров
где ρ — удельное сопротивление вещества, из которого изготовлен проводник; l —длина проводника; S — площадь поперечного сечения проводника.
Сопротивление проводников входит в закон Ома для однородного участка цепи I = U / R, из которого и может быть определено R = U / I.
Из последней формулы выходит, что сопротивление проводника постоянно, поскольку, в соответствии с законом Ома, во сколько раз увеличиваем напряжение на концах проводника, во столько же раз возрастает и сила тока в нем. Все выше описанное также экспериментально было подтверждено на практических опытах
Но практике также выявилось, что можно наблюдать и другие явления. Составив электрическую цепь, схема которой показана на рис. 1. В этой цепи есть источник тока с регулированным напряжением, электрическая лампа, например автомобильная, вольтметр и амперметр, показывающие напряжение на лампе и силу тока в ней. Устанавливаем на лампе напряжение U1 и отмечаем силу тока I1. Если теперь увеличить напряжение, например в 2 раза (U2 = 2U1), то по закону Ома и сила тока должна увеличиться в 2 раза (I2 = 2I1). Однако амперметр показывает силу тока значительно меньшую, чем 2I1. Следовательно, в данном случае закон Ома не выполняется.
Рис. 1. Электрическая цепь с лампой накала
Возникло несоответствие между нашими предшествующими знаниями и новым для вас фактом — закон Ома не всегда справедлив.
Анализ дополнительной литературы и сети интернет существенно расширил наши познания в изученных закономерностях. Еще Ом в своих работах описывал об изменении проводящих свойств металлов как при нагревании так и при остывании. Нами была найдена зависимость сопротивления проводников от температуры, отличной от стандартной, которую можно выразить через следующую формулу:
Константа "альфа" (α) известна как температурный коэффициент сопротивления, который равен относительному изменению электрического сопротивления участка электрической цепи или удельного сопротивления вещества при изменении температуры на единицу. Так как все материалы обладают определенным удельным сопротивлением (при температуре 20 ° С), их сопротивление будет изменяться на определенную величину в зависимости от изменения температуры. Для чистых металлов температурный коэффициент сопротивления является положительным числом, что означает увеличение их сопротивления с ростом температуры. Для таких элементов, как углерод, кремний и германий, этот коэффициент является отрицательным числом, что означает уменьшение их сопротивления с ростом температуры. У некоторых металлических сплавов температурный коэффициент сопротивления очень близок к нулю, что означает крайне малое изменение их сопротивления при изменении температуры.
Теперь возникает вопрос почему так происходит, что с ростом температуры проводника ухудшаются его проводящие свойства. Как мы уже знаем высокая электропроводность металлов связана с тем, что в них имеется большое количество носителей тока — электронов проводимости, образующихся из валентных электронов атомов металла, которые не принадлежат определённому атому. Электрический ток в металле возникает под действием внешнего электрического поля, которое вызывает упорядоченное движение электронов. Движущиеся под действием поля электроны рассеиваются на неоднородностях ионной решётки (на примесях, дефектах решётки, а также нарушениях периодической структуры, связанной с тепловыми колебаниями ионов). При этом электроны теряют импульс, а энергия их движения преобразуются во внутреннюю энергию кристаллической решётки, что и приводит к нагреванию проводника при прохождении по нему электрического тока. Значит, теперь можем сделать вывод, что структура кристаллической решётки влияет на прохождение заряжённых частиц, а как мы уже знаем с ростом температуры происходит увеличение кинетической энергии, тем самым колебания ионных узлов решетки становятся значительными, влияя на периодичность структуры, образуя преграду для прохождения упорядоченного потока электронов, и этим увеличивая сопротивление проводника.
Полупроводники в свою очередь при низких температурах наоборот страдают недостатком носителей электрических зарядов. По этому при их нагревании количество носителей возрастает, что приводит к снижению сопротивления. Если иметь в виду, что размеры металлов при нагревании изменяются мало, то соответствующую формулу можно записать и для удельного сопротивления металлических проводников
Тщательные исследования показывают, что сопротивление металлических проводников зависит от их температуры практически линейно и график такой зависимости представлен на рис. 2.
Рис 2. График зависимости сопротивления металлического проводника от температуры.
2. Исследования проводников
Одним из возможных способов изучения и демонстрации зависимости электрического сопротивления проводника от температуры может служить лабораторная установка. Такая установка была реализована по схеме (рис. 1.) и в ее состав вошли:
1) регулируемый низковольтный источник напряжения
2) автомобильная лампа накаливания на 12 вольт
3) в качестве вольтметра использовался цифровой мультиметр VC 9808
4) роль амперметра выполнил цифровой мультиметр DT -832
Рис. 1. Электрическая цепь с лампой накала

В ходе эксперимента была составлена вольт- амперная характеристика (таблица 1) , которая потвердела выше изложенные доводы.
Читайте также:
