Удельное электрическое сопротивление металлов возрастает в ряду
Удельное сопротивление металлов является мерой их свойства противодействовать прохождению электрического тока. Эта величина выражается в Ом-метр (Ом⋅м). Символ, обозначающий удельное сопротивление, является греческая буква ρ (ро). Высокое удельное сопротивление означает, что материал плохо проводит электрический заряд.
Удельное сопротивление
Удельное электрическое сопротивление определяется как отношение между напряженностью электрического поля внутри металла к плотности тока в нем:
где:
ρ — удельное сопротивление металла (Ом⋅м),
Е — напряженность электрического поля (В/м),
J — величина плотности электрического тока в металле (А/м2)
Если напряженность электрического поля (Е) в металле очень большая, а плотность тока (J) очень маленькая, это означает, что металл имеет высокое удельное сопротивление.
Обратной величиной удельного сопротивления является удельная электропроводность, указывающая, насколько хорошо материал проводит электрический ток:
σ — проводимость материала, выраженная в сименс на метр (См/м).
Электрическое сопротивление
Электрическое сопротивление, одно из составляющих закона Ома, выражается в омах (Ом). Следует заметить, что электрическое сопротивление и удельное сопротивление — это не одно и то же. Удельное сопротивление является свойством материала, в то время как электрическое сопротивление — это свойство объекта.
Электрическое сопротивление резистора определяется сочетанием формы и удельным сопротивлением материала, из которого он сделан.
Например, проволочный резистор, изготовленный из длинной и тонкой проволоки имеет большее сопротивление, нежели резистор, сделанный из короткой и толстой проволоки того же металла.
В тоже время проволочный резистор, изготовленный из материала с высоким удельным сопротивлением, обладает большим электрическим сопротивлением, чем резистор, сделанный из материала с низким удельным сопротивлением. И все это не смотря на то, что оба резистора сделаны из проволоки одинаковой длины и диаметра.

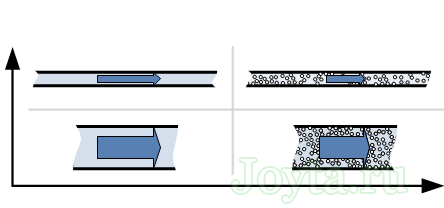
В качестве наглядности можно провести аналогию с гидравлической системой, где вода прокачивается через трубы.
- Чем длиннее и тоньше труба, тем больше будет оказано сопротивление воде.
- Труба, заполненная песком, будет больше оказывать сопротивление воде, нежели труба без песка
Сопротивление провода
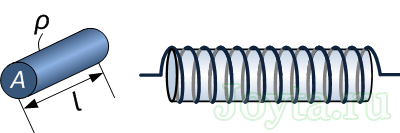
Величина сопротивления провода зависит от трех параметров: удельного сопротивления металла, длины и диаметра самого провода. Формула для расчета сопротивления провода:
где:
R — сопротивление провода (Ом)
ρ — удельное сопротивление металла (Ом.m)
L — длина провода (м)
А — площадь поперечного сечения провода (м2)
В качестве примера рассмотрим проволочный резистор из нихрома с удельным сопротивлением 1.10×10-6 Ом.м. Проволока имеет длину 1500 мм и диаметр 0,5 мм. На основе этих трех параметров рассчитаем сопротивление провода из нихрома:
R=1,1*10 -6 *(1,5/0,000000196) = 8,4 Ом
Нихром и константан часто используют в качестве материала для сопротивлений. Ниже в таблице вы можете посмотреть удельное сопротивление некоторых наиболее часто используемых металлов.

Поверхностное сопротивление
Величина поверхностного сопротивления рассчитывается таким же образом, как и сопротивление провода. В данном случае площадь сечения можно представить в виде произведения w и t:
Для некоторых материалов, таких как тонкие пленки, соотношение между удельным сопротивлением и толщиной пленки называется поверхностное сопротивление слоя RS:
где RS измеряется в омах. При данном расчете толщина пленки должна быть постоянной.
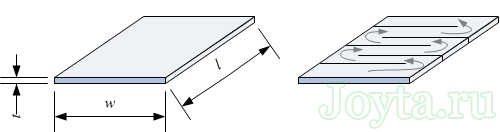
Часто производители резисторов для увеличения сопротивления вырезают в пленке дорожки, чтобы увеличить путь для электрического тока.
Свойства резистивных материалов
Удельное сопротивление металла зависит от температуры. Их значения приводится, как правило, для комнатной температуры (20°С). Изменение удельного сопротивления в результате изменения температуры характеризуется температурным коэффициентом.
Например, в термисторах (терморезисторах) это свойство используется для измерения температуры. С другой стороны, в точной электронике, это довольно нежелательный эффект.
Металлопленочные резисторы имеют отличные свойства температурной стабильности. Это достигается не только за счет низкого удельного сопротивления материала, но и за счет механической конструкции самого резистора.
Много различных материалов и сплавов используются в производстве резисторов. Нихром (сплав никеля и хрома), из-за его высокого удельного сопротивления и устойчивости к окислению при высоких температурах, часто используют в качестве материала для изготовления проволочных резисторов. Недостатком его является то, что его невозможно паять. Константан, еще один популярный материал, легко паяется и имеет более низкий температурный коэффициент.
Удельная проводимость металлов таблица
Электрическое сопротивление, одно из составляющих закона Ома, выражается в омах (Ом). Следует заметить, что электрическое сопротивление и удельное сопротивление — это не одно и то же. Удельное сопротивление является свойством материала, в то время как электрическое сопротивление — это свойство объекта.
Электрическое сопротивление резистора определяется сочетанием формы и удельным сопротивлением материала, из которого он сделан.
Например, проволочный резистор, изготовленный из длинной и тонкой проволоки имеет большее сопротивление, нежели резистор, сделанный из короткой и толстой проволоки того же металла.
В тоже время проволочный резистор, изготовленный из материала с высоким удельным сопротивлением, обладает большим электрическим сопротивлением, чем резистор, сделанный из материала с низким удельным сопротивлением. И все это не смотря на то, что оба резистора сделаны из проволоки одинаковой длины и диаметра.
В качестве наглядности можно провести аналогию с гидравлической системой, где вода прокачивается через трубы.
- Чем длиннее и тоньше труба, тем больше будет оказано сопротивление воде.
- Труба, заполненная песком, будет больше оказывать сопротивление воде, нежели труба без песка
Проводимость и сопротивление
У.с. показывает способность вещества препятствовать прохождению тока. Но в физике есть и обратная величина — проводимость. Она показывает способность проводить электрический ток. Выглядит она так:
σ=1/ρ, где ρ – это и есть удельное сопротивление вещества.
Если говорить о проводимости, то она определяется характеристиками носителей зарядов в этом веществе. Так, в металлах есть свободные электроны. На внешней оболочке их не больше трех, и атому выгоднее их «отдать», что и происходит при химических реакциях с веществами из правой части таблицы Менделеева. В ситуации же, когда мы располагаем чистым металлом, он имеет кристаллическую структуру, в которой эти наружные электроны общие. Они-то и переносят заряд, если приложить к металлу электрическое поле.
В растворах носителями заряда являются ионы.
Если говорить о таких веществах, как кремний, то по своим свойствам он является полупроводником и работает несколько по иному принципу, но об этом позже. А пока разберемся, чем же отличаются такие классы веществ, как:
Читать также: Фото лесоруба с бензопилой
Проводники и диэлектрики
Есть вещества, которые ток почти не проводят. Они называются диэлектриками. Такие вещества способны поляризоваться в электрическом поле, то есть их молекулы могут поворачиваться в этом поле в зависимости от того, как распределены в них электроны. Но поскольку электроны эти не являются свободными, а служат для связи между атомами, ток они не проводят.
Проводимость диэлектриков почти нулевая, хотя идеальных среди них нет (это такая же абстракция, как абсолютно черное тело или идеальный газ).
Условной границей понятия «проводник» является ρ
Удельное сопротивление металлов является мерой их свойства противодействовать прохождению электрического тока. Эта величина выражается в Ом-метр (Ом⋅м). Символ, обозначающий удельное сопротивление, является греческая буква ρ (ро). Высокое удельное сопротивление означает, что материал плохо проводит электрический заряд.
Сопротивление провода
Величина сопротивления провода зависит от трех параметров: удельного сопротивления металла, длины и диаметра самого провода. Формула для расчета сопротивления провода:
где: R — сопротивление провода (Ом) ρ — удельное сопротивление металла (Ом.m) L — длина провода (м) А — площадь поперечного сечения провода (м2)
В качестве примера рассмотрим проволочный резистор из нихрома с удельным сопротивлением 1.10×10-6 Ом.м. Проволока имеет длину 1500 мм и диаметр 0,5 мм. На основе этих трех параметров рассчитаем сопротивление провода из нихрома:
R=1,1*10-6*(1,5/0,000000196) = 8,4 Ом
Нихром и константан часто используют в качестве материала для сопротивлений. Ниже в таблице вы можете посмотреть удельное сопротивление некоторых наиболее часто используемых металлов.

Какое сопротивление меди и алюминия
Алюминий — это легкий металл, который легко поддается обработке и литью. Обладает высокой электропроводностью: он стоит на 4 месте после серебра, меди и золота.
Важно! Несмотря на ряд достоинств (невысокую стоимость, малый вес, простоту обработки и другие) в долгосрочной перспективе алюминиевые провода менее выгодны, чем медные.
В электротехнике значение имеют 2 термина:
- Электропроводность: отвечает за передачу тока от одной точки к другой. Чем выше проводимость металла, тем лучше он передает электричество. При +20 градусах проводимость меди составляет 59,5 миллионов сименс на метр (См/м), алюминия — 38 миллионов См/м. Проводимость медного кабеля практически не зависит от температуры.
- Электросопротивление: чем выше это понятие, тем хуже вещество будет пропускать ток. Удельное сопротивление меди составляет 0,01724-0,0180 мкОм/м, алюминия — 0,0262-0,0295.
Вам это будет интересно Особенности мощности постоянного тока

Алюминиевые кабели востребованы не меньше медных
Иными словами, медь обладает более высокой проводимостью и меньшим сопротивлением, чем алюминий.
Свойства резистивных материалов
Удельное сопротивление металла зависит от температуры. Их значения приводится, как правило, для комнатной температуры (20°С). Изменение удельного сопротивления в результате изменения температуры характеризуется температурным коэффициентом.
Например, в термисторах (терморезисторах) это свойство используется для измерения температуры. С другой стороны, в точной электронике, это довольно нежелательный эффект. Металлопленочные резисторы имеют отличные свойства температурной стабильности. Это достигается не только за счет низкого удельного сопротивления материала, но и за счет механической конструкции самого резистора.
Много различных материалов и сплавов используются в производстве резисторов. Нихром (сплав никеля и хрома), из-за его высокого удельного сопротивления и устойчивости к окислению при высоких температурах, часто используют в качестве материала для изготовления проволочных резисторов. Недостатком его является то, что его невозможно паять. Константан, еще один популярный материал, легко поддается пайке и имеет более низкий температурный коэффициент.
Удельное сопротивление металлов, электролитов и веществ (Таблица)
Удельное сопротивление металлов и изоляторов
В справочной таблице даны значения удельного сопротивления р некоторых металлов и изоляторов при температуре 18—20° С, выраженные в ом·см. Величина р для металлов в сильной степени зависит от примесей, в таблице даны значения р для химически чистых металлов, для изоляторов даны приближенно. Металлы и изоляторы расположены в таблице в порядке возрастающих значений р.
Таблица удельное сопротивление металлов
| Чистые металлы | 104 ρ (ом·см) | Чистые металлы | 104 ρ (ом·см) |
| Серебро | 0,016 | Хром | 0,131 |
| Медь | 0,017 | Тантал | 0,146 |
| Золото | 0,023 | Бронза 1) | 0,18 |
| Алюминий | 0,029 | Торий | 0,18 |
| Дюралюминий | 0,0335 | Свинец | 0,208 |
| Магний | 0,044 | Платинит 2) | 0,45 |
| Кальций | 0,046 | Сурьма | 0,405 |
| Натрий | 0,047 | Аргентан | 0,42 |
| Марганец | 0,05 | Никелин | 0,33 |
| Иридий | 0,063 | Манганин | 0,43 |
| Вольфрам | 0,053 | Константан | 0,49 |
| Молибден | 0,054 | Сплав Вуда 3) | 0,52 (0°) |
| Родий | 0,047 | Осмий | 0,602 |
| Цинк | 0,061 | Сплав Розе 4) | 0,64 (0°) |
| Калий | 0,066 | Хромель | 0,70-1,10 |
| Никель | 0,070 | ||
| Кадмий | 0,076 | Инвар | 0,81 |
| Латунь | 0,08 | Ртуть | 0,958 |
| Кобальт | 0,097 | Нихром 5) | 1,10 |
| Железо | 0,10 | Висмут | 1,19 |
| Палладий | 0,107 | Фехраль 6) | 1,20 |
| Платина | 0,110 | Графит | 8,0 |
| Олово | 0,113 |
Таблица удельное сопротивление изоляторов
| Изоляторы | ρ (ом·см) | Изоляторы | ρ (ом·см) |
| Асбест | 108 | Слюда | 1015 |
| Шифер | 108 | Миканит | 1015 |
| Дерево сухое | 1010 | Фарфор | 2·1015 |
| Мрамор | 1010 | Сургуч | 5·1015 |
| Целлулоид | 2·1010 | Шеллак | 1016 |
| Бакелит | 1011 | Канифоль | 1016 |
| Гетинакс | 5·1011 | Кварц _|_ оси | 3·1016 |
| Алмаз | 1012 | Сера | 1017 |
| Стекло натр | 1012 | Полистирол | 1017 |
| Стекло пирекс | 2·1014 | Эбонит | 1018 |
| Кварц || оси | 1014 | Парафин | 3·1018 |
| Кварц плавленый | 2·1014 | Янтарь | 1019 |
Удельное сопротивление чистых металлов при низких температурах
В таблице даны значения удельного сопротивления (в ом·см) некоторых чистых металлов при низких температурах (0°С).
| Чистые металлы | t (°С) | Удельное сопротивление, 104 ρ (ом·см) |
| Висмут | -200 | 0,348 |
| Золото | -262,8 | 0,00018 |
| Железо | -252,7 | 0,00011 |
| Медь | -258,6 | 0,00014 1 |
| Платина | -265 | 0,0010 |
| Ртуть | -183,5 | 0,0697 |
| Свинец | -252,9 | 0,0059 |
| Серебро | -258,6 | 0,00009 |
Отношение сопротивлении Rt/Rq чистых металлов при температуре Т °К и 273° К.
В справочной таблице дано отношение Rt/Rq сопротивлений чистых металлов при температуре Т °К и 273° К.
| Чистые металлы | Т (°К) | RT/R0 |
| Алюминий | 77,7 | 1,008 |
| 20,4 | 0,0075 | |
| Висмут | 77,8 | 0,3255 |
| 20,4 | 0,0810 | |
| Вольфрам | 78,2 | 0,1478 |
| 20,4 | 0,0317 | |
| Железо | 78,2 | 0,0741 |
| 20,4 | 0,0076 | |
| Золото | 78,8 | 0,2189 |
| 20,4 | 0,0060 | |
| Медь | 81,6 | 0,1440 |
| 20,4 | 0,0008 | |
| Молибден | 77,8 | 0,1370 |
| 20,4 | 0,0448 | |
| Никель | 78,8 | 0,0919 |
| 20,4 | 0,0066 | |
| Олово | 79,0 | 0,2098 |
| 20,4 | 0,0116 | |
| Платина | 91,4 | 0,2500 |
| 20,4 | 0,0061 | |
| Ртуть | 90,1 | 0,2851 |
| 20,4 | 0,4900 | |
| Свинец | 73,1 | 0,2321 |
| 20,5 | 0,0301 | |
| Серебро | 78,8 | 0,1974 |
| 20,4 | 0,0100 | |
| Сурьма | 77,7 | 0,2041 |
| 20,4 | 0,0319 | |
| Хром | 80,0 | 0,1340 |
| 20,6 | 0,0533 | |
| Цинк | 83,7 | 0,2351 |
| 20,4 | 0,0087 |
Удельное сопротивление электролитов
В таблице даны значения удельного сопротивления электролитов в ом·см при температуре 18° С. Концентрация растворов с дана в процентах, которые определяют число граммов безводной соли или кислоты в 100 г раствора.
| c (%) | NH4Cl | NaCl | ZnSO4 | CuSO4 | КОН | NaOH | H2SO4 |
| 5 | 10,9 | 14,9 | 52,4 | 52,9 | 5,8 | 5,1 | 4,8 |
| 10 | 5,6 | 8,3 | 31,2 | 31,3 | 3,2 | 3,2 | 2,6 |
| 15 | 3,9 | 6,1 | 24,1 | 23,8 | 2,4 | 2,9 | 1,8 |
| 20 | 3,0 | 5,1 | 21,3 | — | 2,0 | 3,0 | 1,5 |
| 25 | 2,5 | 4,7 | 20,8 | — | 1,9 | 3,7 | 1,4 |
_______________
Источник информации: КРАТКИЙ ФИЗИКО-ТЕХНИЧЕСКИЙ СПРАВОЧНИК/ Том 1, — М.: 1960.
Состав и структура железа
Железо – типичный металл, причем химически активный. Вещество вступает в реакцию при нормальной температуре, а нагрев или повышение влажности значительно увеличивают его реакционноспособность. Железо корродирует на воздухе, горит в атмосфере чистого кислорода, а в виде мелкой пыли способно воспламениться и на воздухе.
Чистому железу присуща ковкость, однако в таком виде металл встречается очень редко. На деле под железом подразумевают сплав с небольшими долями примесей – до 0,8%, которому присущи мягкость и ковкость чистого вещества. Значение для народного хозяйства имеет сплавы с углеродом – сталь, чугун, нержавеющая сталь.
Железу присущ полиморфизм: выделяют целых 4 модификации, отличающиеся структурой и параметрами решетки:
При высоком давлении, а также при легировании металла некоторыми добавками образуется ε- фаза с гексагонической плотноупакованной решеткой.
Температура фазовых переходов заметно изменяется при легировании тем же углеродом. Собственно, сама способность железа образовать столько модификаций служит основой обработки стали в разных температурных режимах. Без таких переходов металл не получил бы столь широкого распространения.
Электрическое сопротивление металлов. Сверхпроводимость
1. Электрическое сопротивление металлов. Квантовая теория электропроводности металлов сводится к следующему:
а. В идеальной кристаллической решетке электроны проводимости при своем движении не должны испытывать сопротивления. Сопротивление возникает тогда, когда в решетке появляются дефекты структуры, то есть нарушается периодичность решетки.
б. В реальных кристаллах есть два механизма нарушения структуры: примесный и тепловой. Соответственно различают примесное удельное сопротивление rn и тепловое (колебательное) rТ. Согласно правилу аддитивности сопротивлений полное сопротивление металла r равно их сумме, r = rn + rТ. (13.1)
в. Примесное сопротивление rn обусловлено наличием инородных атомов в решетке (атомов примеси). Если металл достаточно чистый и концентрация атомов примеси невелика, то примесное сопротивление практически не зависит от температуры и становиться заметным лишь вблизи абсолютного нуля. Благодаря примеси удельное сопротивление металла не должно обращаться в нуль даже при Т = 0 К.
г. Тепловое сопротивление rТ возникает благодаря рассеянию электронов проводимости на флуктуациях плотности узлов кристаллической решетки, возникающих при тепловом колебательном движении узлов. В квантовой теории тепловое колебательное движение атомов решетки трактуется как система стоячих звуковых волн в кристалле - фононов. Поэтому говорят о рассеянии электронов проводимости на фононах.
В отличие от классической теории электропроводности металлов Друде - Лоренца, прогнозирующей зависимость сопротивления от температуры вида r ~ , квантовая теория дает правильный прогноз линейной зависимости r ~Т. При температурах металла Т ³ 50 К r = r0aТ, что соответствует эмпирической формуле r = r0(1 + a t). В квантовой теории получается, что при Т ® 0 полное удельное сопротивление металла r должно стремиться к примесному rn. На рис.90 показана опытная зависимость удельного сопротивления чистого натрия от температуры.
При Т ® 0 К r ® rn = 4·10 -11 Ом·м, что составляет примерно 0,4% от сопротивления при Т = 273 К. Уже при температурах Т ³ 20 К зависимость r(Т) становится практически линейной.
д. Электрический ток толкуется в квантовой теории как дрейф электронов в периодическом поле кристалла. Этот дрейф происходит под действием постоянной электрической силы еЕ, где Е- напряженность электрического поля, создающего ток. Оказалось, что скорость дрейфа электронов зависит от глубины их положения в зоне проводимости. Эта зависимость выражается через эффективную массу mэф электрона. В отличие от массы покоя mе свободного электрона эффективная масса электрона в зоне проводимости металла – величина переменная, зависящая от ширины зоны.
Вблизи дна зоны эффективная масса электронов положительна. Направление дрейфа соответствует вектору плотности тока. По мере подъема к верхней границе зоны эффективная масса принимает бесконечно большое значение mэф = ¥, а затем становится отрицательной. Соответственно и скорость дрейфа электронов, имея “правильное” направление у дна зоны, постепенно проходит через нуль и принимает отрицательные (“неправильные”) значения у верхней границы зоны.
Соотношения, полученные в приближении свободных электронов в теории Друде – Лоренца, оказываются справедливыми для электронов, движущихся в периодическом поле решетки, если в них заменить массу покоя электрона mе на эффективную mэф.
2. Сверхпроводимость. В 1911 году Камерлинг – Оннес, измеряя сопротивление ртути в области низких температур, обнаружил, что при Т = 4,2 К сопротивление ртути практически падало до нуля. Это явление стали называть сверхпроводимостью. На рис.91 показаны опытные кривые зависимости удельного сопротивления некоторых чистых металлов от температуры вблизи абсолютного нуля. Очевидно, что явление не сводится к нормальному падению удельного сопротивления бездефектного кристалла, когда rn = 0, и rТ . Переход в сверхпроводящее состояние происходит не плавно, а скачкообразно при некоторой температуре Ткр, которую называют критической температурой перехода. Сейчас известно около 30 сверхпроводящих химических элементов и свыше 500 сверхпроводящих материалов.
3. Эффекты сверхпроводимости.
а. Электрический ток, возбужденный в сверхпроводящем кольце, может циркулировать в нем годами.
б. ЭффектМейснера. В 1933 году Вальтер Мейсснер и Р. Оксенфельд обнаружили, что вещество, помещенное в магнитное поле (рис.92 слева), при переходе в сверхпроводящее состояние не замораживает находящееся в нем магнитное поле, как это должно было быть при простом переходе вещества в состояние с нулевым сопротивлением, а выталкивает его из своего объема (рис. 92 справа). Это присуще идеальным диамагнетикам с нулевой магнитной проницаемостью m = 0.
Из того, что магнитное поле не проникает в сверхпроводник, следует, что электрический ток может течь лишь по поверхности сверхпроводника. Ведь если бы ток мог протекать в толще сверхпроводника, то вокруг него в толще сверхпроводника было бы магнитное поле. И действительно, опыт показывает, что электрический ток течет в сверхпроводнике в поверхностном слое толщиной l = 10 ¸ 100 нм. На эту глубину в сверхпроводник проникает и магнитное поле, убывая с расстоянием x от поверхности по экспоненциальному закону
В = В0exp(-xçl). (13.2)
Вещество в сверхпроводящем состоянии приобретает два не связанных друг с другом фундаментальных свойства: идеальную проводимость и идеальный диамагнетизм.
Эффект Мейснера позволяет устойчиво подвешивать сверхпроводящие тела в магнитном поле (рис.93). При пререходе шара в сверхпроводящее состояние 1-го рода магнитное поле из него вытесняется. В результате в поверхностном слое шара индуцируется ток такого направления, при котором шар выталкивается из поля.
в. Эффект критического магнитного поля. Он состоит в том, что при достижении магнитным полем, в котором находится сверхпроводник, некоторого предельного значенияиндукции Вкр »10 -2 ¸ 10 1 Тл, сверхпроводимость исчезает.
На рис.94 показана зависимость Вкр от температуры для свинца (верхняя кривая) и для олова (нижняя кривая). При критической температуре Т = Ткр критическое поле равно нулю, Вкр = 0, а с понижением температуры Вкр увеличивается.
Если усиливать ток, идущий по сверхпроводнику, то при некотором его критическом значении Iкр сверхпроводящее состояние разрушается. Поскольку магнитное поле В пропорционально току I, то зависимость Iкр от температуры аналогична зависимости Вкр(Т). Эффект критического магнитного поля усложняет технику получения сверхсильных магнитных полей с помощью сверхпроводящих контуров. Расчет критического тока должен учитывать, что ток течет в приповерхностном слое. Например, у проводника диаметром 1 мм при l = 35 нм сечение приповерхностного слоя, по которому течет ток, около 10 -4 мм 2 . Это составляет около 0,01% всего сечения проводника.
г. Эффект Джозефсона. В 1962 году Брайан Джозефсон теоретически предсказал два эффекта, суть которых в следующем.
Подсоединим к сверхпроводнику (на рис.95-а он изображен в виде бруска) амперметр А с источником постоянного тока, ЭДС которого E, и вольтметр V. В цепи идёт постоянный ток, регистрируемый амперметром. Так как сопротивление сверхпроводника равно нулю, то вольтметр показывает нуль.
Разрежем сверхпроводник на две части и раздвинем их, чтобы между ними возник зазор толщиной d » 1 нм. Как предсказал Джозефсон, при включении такого сверхпроводника в цепь может наблюдаться один из следующих двух эффектов.
Стационарный эффект Джозефсона. Через сверхпроводник по-прежнему идёт постоянный ток. Оказывается, ток может течь без сопротивления не только через сверхпроводник, но и через щель в нем, если она достаточно узка (рис.95-б).
Нестационарный эффект Джозефсона. На концах сверхпроводника со щелью может возникнуть постоянная разность потенциалов. В этом случае из щели излучается высокочастотная электромагнитная волна (рис.95-в). Через сверхпроводник течет не только постоянный, но и высокочастотный переменный ток.
В настоящее время эффекты Джозефсона не только подтверждены экспериментально, но и используются в микроэлектронике.
4. Теорию сверхпроводимости построили в 1957г Джон Бардин, Леон Купер и Джон Шриффер. По первым буквам их фамилий ее назвали БКШ – теорией. В основе БКШ- теории лежит представление, что между электронами проводимости металла могут действовать силы притяжения, возникающие вследствие поляризации ими кристаллической решетки.
Электрон, движущийся в решетке, притягивает к себе положительно заряженные ионы, несколько сближая их, и тем самым создает вдоль пути своего следования избыточный положительный заряд поляризованной решетки, к которому могут быть притянуты другие электроны. Это эквивалентно возникновению силы притяжения между электронами, только действующей не непосредственно, а через поляризованную решетку.
Можно предположить, что сверхпроводимость следует ожидать прежде всего у тех металлов, у которых имеет место сильное взаимодействие электронного газа с решеткой, приводящее в обычных условиях к высокому удельному сопротивлению. И действительно, из чистых металлов лучшими сверхпроводниками оказались наиболее высокоомные - свинец Рb, ниобий Nb, олово Sn, ртуть Hg. В то же время у таких низкоомных металлов, как медь Cuи сереброAg, у которых электронный газ имеет высокую подвижность, сверхпроводимость не наблюдается.
Как показал Леон Купер, при Т < Ткр, самые верхние электроны,расположенные на уровне Ферми, могут спариваться. При этом их суммарная энергия оказывается меньше суммы энергий отдельных электронов. Выделяющаяся энергия должна отводиться от кристалла охлаждением. Понижение энергии куперовских пар приводит к понижению верхнего занятого электронами уровня. В результате между уровнями куперовских пар и ближайшими свободными уровнями возникает запрещенная зона шириной 2D (рис.96 слева). Эта возникшая энергетическая щель не позволяет куперовским парам электронов принимать малую энергию. Они могут принять лишь энергию не менее 2D, которая позволит электронам перепрыгнуть через эту щель. Поэтому при Т < Ткр куперовские пары оказываются весьма устойчивыми.
При Т < Ткр спариваются не все электроны. При каждой температуре устанавливается некоторое равновесное соотношение между концентрациями нормальных и спаренных электронов. Оказывается, что ширина 2D энергетической щели в сверхпроводнике зависит от количества неспаренных электронов. Их концентрация понижается с уменьшением температуры и соответственно растет ширина щели (рис.96 справа).
Электроны, образующие куперовские пары, имеют противоположные спины. Поэтому спин пары равен нулю, и она представляет собой бозон. Бозоны могут накапливаться в основном энергетическом состоянии, из которого их трудно перевести в возбужденное состояние. Поэтому куперовские пары в состоянии согласованного движения могут оставаться неопределенно долго. Такое согласованное движение пар и есть ток сверхпроводимости.
Расстояние между электронами пары велико. Оно составляет примерно 1000 нм, что около 5000 поперечников атомов. Примерно 1000 пар перекрываются, занимая общий объем.
5. Объяснение БКШ – теорией эффекта критического тока. У известных сверхпроводников величина энергетической щели составляет в среднем 2D = 3 мэВ » 5·10 -22 Дж. Для разрушения куперовской пары один из электронов пары должен уменьшить энергию своего движения, по крайней мере, на величину 2D.
Предположим, что электрон отдает эту энергию при лобовом столкновении с узлом решетки так, что после столкновения он отскакивает с той же скоростью дрейфа vд в обратном направлении. Энергия электрона до соударения Ек1 = me(vф + vд) 2 ç2, энергия после соударения Ек2 = me(vф - vд) 2 ç2. Здесь vф – тепловая скорость электронов на уровне Ферми (»10 6 мçс), vд – скорость дрейфа электронов в электрическом поле, она не превышает 1 мçс.
Убыль кинетической энергии электрона должна быть по крайней мере равной 2D. Так что DЕк= = 2mevфvд = 2D. (13.3)
Отсюда, минимальная скорость дрейфа vд, необходимая для разрушения куперовской пары, есть vд = Dçmevф. (13.4)
Плотность электронного тока проводимости естьj = envд, (13.5)
где n – концентрация электронов проводимости в металле. Подставив критическую скорость дрейфа из (13.4), получаем критическую плотность тока jкр.
У типичных сверхпроводников n = 3·10 28 м -3 , vф = 10 6 мçс, 2D = 3 мэВ. Подставляем.
jкр = =10 12 . Это соответствует току 10 6 А через проводник сечением 1 мм 2 . Но в реальном сверхпроводнике ток течет лишь в тонком приповерхностном слое толщиной около 35 нм, что соответствует сечению S = 10 -4 мм 2 . Поэтому критический ток в сверхпроводнике толщиной около 1 мм составляет всего лишь iкр = jкрS = 10 6 Аçмм 2 ·10 - 4 мм 2 = 100 А. Это вполне соответствует эксперименту.
6. Объяснение БКШ-теорией критического магнитного поля. При помещении сверхпроводника в магнитное поле В в поверхностном слое сверхпроводника наводится незатухающий ток. Этот незатухающий ток имеет такие величину и направление, что его магнитное поле внутри сверхпроводника полностью компенсирует внешнее поле В. При увеличении поля В плотность компенсирующего тока в сверхпроводнике растет. Если внешнее поле В будет настолько большим, что плотность наведенного им индукционного тока достигнет критического значения, сверхпроводимость разрушается.
Все выше сказанное относится к сверхпроводникам 1-го рода, в которых электрический ток существует только в приповерхностном слое. Несколько позже были открыты и изучены сверхпроводники 2-го рода. В них возникающие во внешнем магнитном поле В сверхпроводящие токи текут не только по поверхности, но и проникают в толщу проводника. У сверхпроводников 1-го рода критическое магнитное поле Вкр не превышает 0,1 Тл, а у сверхпроводников 2-го рода достигает величины Вкр» 20 Тл.
7. Эффекты Джозефсона объясняются БКШ - теорией как результат туннелирования куперовских пар через узкую щель между сверхпроводниками. Согласно теории, частота n переменного сверхпроводящего тока определяется выражением: n = . (13.7)
При напряжении на щели U = 1 мВ частота n = 485 ГГц, что соответствует длине волны ЭМ излучения l = сçn = 0,6 мм.
8. Реактивное сопротивление сверхпроводника. При любой температуре Т < Ткр сверхпроводник практически всегда содержит как сверхпроводящие электроны концентрацией nc, так и нормальные (nн) электроны. Если поместить сверхпроводник в высокочастотное поле, то в этом переменном электрическом поле ускоряются не только куперовские пары, но и нормальные электроны. Поэтому ток имеет как сверхпроводящую, так и нормальную составляющую.
Те и другие электроны обладают массой, вследствие их инерции ток отстает по фазе от напряженности ВЧ – поля. Куперовские пары движутся в проводнике как бы без трения. Согласно классической механике, скорость частиц в этом случае отстает по фазе от действующей на них периодической силы на pç2. Поэтому сверхпроводящая составляющая высокочастотного тока отстает от напряженности поля на pç2. Это значит, что куперовские пары создают чисто реактивное сопротивление.
Нормальные электроны движутся как бы с трением. Поэтому они создают как реактивное, так и активное сопротивление.
Удельное сопротивление металлов

Величина удельного сопротивления характеризует способность вещества ограничивать электрический ток (оказывать сопротивление). Металлические проводники имеют самые низкие значения удельных сопротивлений, поэтому они используются и для передачи электроэнергии на большие расстояния, и в качестве соединительных проводов в электронных приборах, и соединительных дорожек на платах микросхем. Разберемся почему металлы обладают этим свойством и какие из них лучше всего подходят для этих целей.
Определение удельного сопротивления
Общая формула для вычисления удельного сопротивления ρ любого вещества выглядит следующим образом:
где: R — сопротивление, S — площадь поперечного сечения, L — длина проводника. На основании экспериментальных данных, пользуясь законом Ома и этой формулой, определены удельные сопротивления большого числа материалов, которые приведены в справочниках и на специализированных интернет-ресурсах.
Единицы измерения удельного сопротивления
Из формулы (1) следует, что поскольку в Международной системе СИ сопротивление измеряется в омах, длина и площадь в метрах и метрах квадратных соответственно, то единицей измерения удельного сопротивления будет Ом*м:
Для практических расчетов часто используется внесистемная единица Ом*мм 2 /м. Эта единица равна удельному сопротивлению вещества, из которого сделан проводник длиной 1 м и площадью поперечного сечения 1 мм 2 . Числовые значения для ρ становятся более комфортны для восприятия. Еще одна причина связана с тем, что величины сечений реальных проводов и кабелей составляют 1-10 мм 2 , и для вычисления их параметров внесистемная единица удобнее.
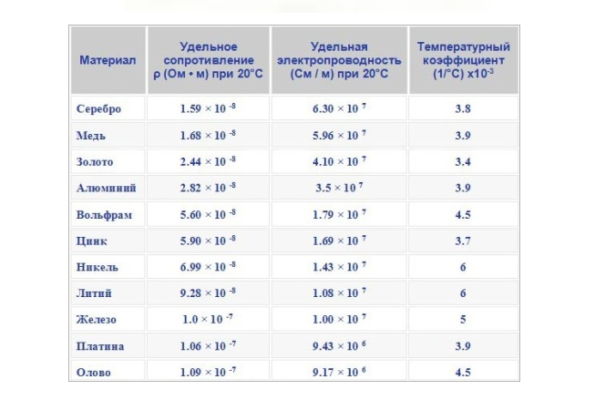
Рис. 1. Таблица удельных сопротивлений различных материалов.
Почему у металлов самые низкие удельные сопротивления
Из приведенной таблицы видно, что самыми низкими значениями удельных сопротивлений обладают металлы: серебро, медь, золото, алюминий и др. Такое свойство металлов связано с большой концентрацией свободных электронов, “не привязанных” к конкретному атому, а блуждающих в пространстве кристаллической решетки. Напряжение, приложенное к концам проводника, создает электрическое поле, которое действует на электроны, заставляя их двигаться согласованно, в одном направлении.
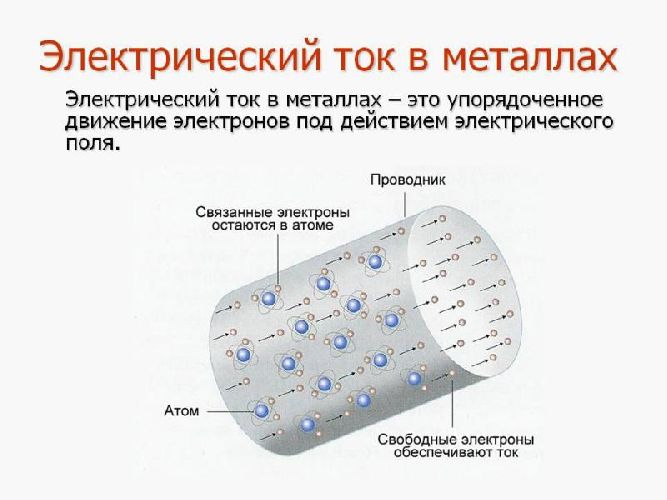
Рис. 2. Электрический ток в металлах, свободные электроны.
Самым низким значением ρ обладает серебро — 0,016 Ом*мм 2 /м. Но для повсеместного, массового, использования в сетях электроснабжения и оборудовании этот металл не используется в виду слишком большой цены. Серебро применяется для создания самых ответственных контактов в специальных электротехнических устройствах. В следующей таблице приведены величины удельных сопротивлений металлов и сплавов, часто используемых металлов в электротехнике:
Удельное сопротивление проводника

Проводниками в физике называют материалы, общим свойством которых является способность хорошо проводить электрический ток. Большое количество свободных носителей электрического заряда (электронов и ионов), имеющееся в проводниках, при воздействии на них электрического поля, создает направленное, упорядоченное перемещение, то есть электрический ток. Величины токов для разных проводников с одинаковыми геометрическими размерами и одинаковой напряженностью электрического поля могут существенно отличаться. Физическая величина, характеризующая способность различных материалов по разному проводить электрический ток, называется удельным электрическим сопротивлением.
Вспомним закон Ома
Основным законом, устанавливающим связь между электрическим напряжением U, током I и сопротивлением R, является закон Ома:
Закон был открыт немецким ученым Георгом Омом в 1826 г. экспериментальным путем. Ученый измерял величину тока при различных напряжениях, которое он варьировал с помощью гальванических батарей, меняя их количество.
От чего зависит величина сопротивления R ?
Дальнейшие эксперименты показали, что:
- Величина R прямо пропорциональна длине проводника, то есть чем больше длина проводник L, тем больше тем больше его сопротивление, причем зависимость линейная, то есть R∼L;
- Величина R , обратно пропорциональна поперечной площади проводника S, то есть $ R ∼ <1\over S >$;
- Поскольку у проводников из разных материалов с одинаковыми размерами S и L сопротивления отличались, то была введена физическая величина, названная удельным сопротивлением ρ.
Тогда выражение для величины сопротивления приобрело следующий вид:
Из уравнения (2) можно получить формулу удельного сопротивления проводника:
Пользуясь формулой (3), можно дать следующее определение: удельное сопротивление — это величина, равная сопротивлению проводника длиной один метр с площадью поперечного сечения в один метр квадратный. Тогда в Международной системе СИ получаем для ρ размерность [Ом*м]:
Оказалось, для практического применения величину ρ удобнее определить как сопротивление проводника длиной один метр с площадью поперечного сечения в один миллиметр квадратный.
Тогда числовые значения ρ, становятся более удобными для восприятия. Например, удельное сопротивление железа ρж = 130000 (Ом*м) = 0,13 (Ом*мм 2 )/м. В справочниках данные приводятся в этом в последнем, более компактном представлении.
Температурная зависимость ρ(Т)
Для большинства материалов проведены многочисленные эксперименты по измерению значений удельных сопротивлений. Данные по большинству проводников можно найти в справочных таблицах.
Удельное сопротивление металлов и сплавов, Ом*мм 2 /м
Чаще всего приводятся значения ρ при нормальной, то есть комнатной температуре 20 0 С. Но оказалось, что при повышении температуры удельное сопротивление возрастает по линейному закону в соответствии с формулой:
$ ρ(Т) = ρ0 * (1 + α*T)$ (6),
где: ρ0 — удельное сопротивление проводника при температуре 0 0 С, α — температурный коэффициент удельного сопротивления, который тоже имеет для каждого вещества свое, индивидуальное, значение. Из формулы (6) следует, что коэффициент α имеет размерность [ 0 C -1 ] или [ 1\ 0 C ].
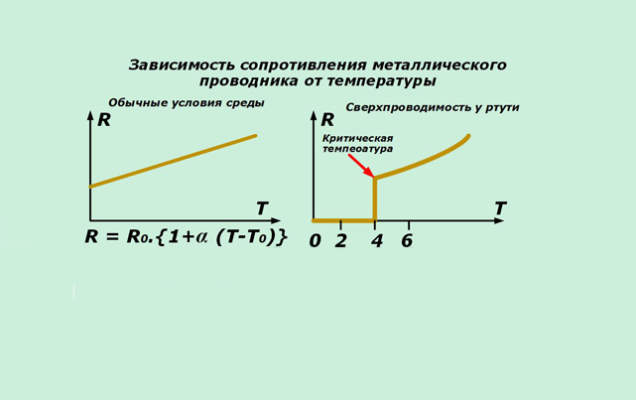
Рис. 2. Температурная зависимость удельного сопротивления проводника
В соответствии с законом Джоуля-Ленца при протекании электрического тока т выделяется тепло, а значит происходит рост температуры проводника. Кроме этого, в зависимости от области применения, электрические приборы могут работать как при пониженных (минусовых), так и при высоких температурах. Для точных расчетов электрических цепей необходимо учитывать зависимость ρ(Т). Величину α для конкретного материала можно узнать из справочной литературы.
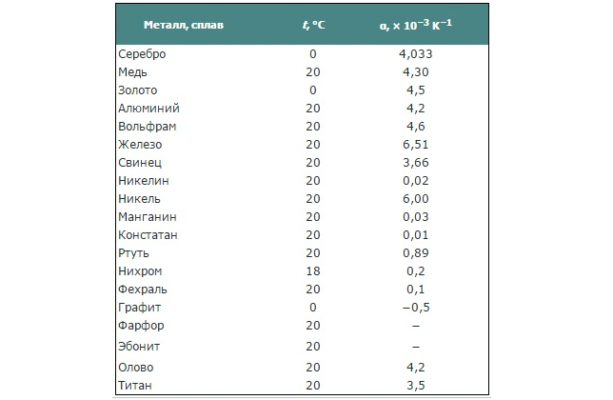
Рис. 3. Справочные значения температурного коэффициента удельного сопротивления проводников
Что мы узнали?
Итак, мы узнали, что величина, характеризующая способность различных материалов по разному проводить электрический ток, называется удельным электрическим сопротивлением. Приведена формула (3) для определения удельного сопротивления проводника ρ. Линейная температурная зависимость удельного сопротивления ρ(Т) описывается формулой (6).
Читайте также:
