Теоретическая и фактическая прочность металлов

Обновлено: 22.01.2025

Рассчитанная прочность в отличие от найденной экспериментально называется теоретической.

Теоретическая прочность зависит от природы сил взаимодействия между частицами (ионная, ковалентная, металлическая связь и др.) и от структуры материала.

Например, Орован предложил формулу

где - свободная поверхностная энергия твердого тела;

Е - модуль упругости при растяжении;

х - равновесное межчастичное расстояние.

Более упрощенной является зависимость

Реальная прочность (техническая) твердых тел на два - три порядка меньше теоретической, так как в материале есть микротрещины различных размеров и ориентации. Трещины являются концентраторами напряжения, напряжение на их краях может быть во много раз больше среднего напряжения в сечение образца.

Если величина перенапряжения () у вершины наиболее опасной трещины равна теоретической прочности (), то происходит быстрый рост трещины и образец разделяется на две части. Приложенное напряжение при этом соответствует так называемой максимальной технической прочности ().

Коэффициент концентрации напряжения в вершине микротрещины равен. Он зависит от формы и размеров трещины, ее ориентации по отношению к направлению растяжения. Поэтому максимальная техническая прочность не является константой материала.

Максимальную техническую прочность Гриффитс рассчитывал из условия: трещина растет только тогда, когда уменьшение упругой энергии в образце в процессе ее роста (за счет разгрузки материала вокруг растущей трещины) равно или больше увеличения потенциальной энергии, происходящего при образовании новых поверхностей разрыва. (По русски: прочность зависит от поверхностной энергии, когда образец рвется поверхностная (потенциальная) энергия увеличивается, а упругая энергия уменьшается. Когда Упр. Эн. Уменьшается сильнее чем увеличиваеться Пот. Эн. Образчу пиздец)

Формула Гриффитса. Изменение упругой энергии (ΔW) в образце в виде тонкой пластинки при образовании в ней трещины длиной (С), ориентированной перпендикулярно направлению растяжения, равно

где δ - толщина пластинки; μ - коэффициент Пуассона.

Изменение упругой энергии является отрицательной величиной. Поверхностная энергия трещины длиной (с) равна (). Следовательно, при увеличении длины трещины на малую величину (d_c) упругая энергия уменьшается согласно выражению (3.2) на . Одновременно поверхностная энергия увеличивается на .

По Гриффитсу условием разрушения является равенство этих изменений энергии. Из этого следует, что максимальная техническая прочность пластинки с внутренней трещиной длиной (с) равна

в случае плоского напряженного состояния.

При наличии краевой микротрещины, длина которой l вдвое меньше длины внутренней трещины

Из этих формул следует, что в средах, уменьшающих свободную поверхностную энергию, прочность уменьшается.

Дальнейшие исследования позволили уточнить условии, при которых трещина Гриффитса будет расти или смыкаться

(Изменение энергии (W) при образовании в ней трещины длиной (С))

Если длина трещины больше критической длины, то дальнейшее ее увеличение приведет к уменьшению общей энергии образца и трещина должна самопроизвольно расти.

Если трещина меньше критической, то к уменьшению общей энергии приведет ее уменьшение и трещина должна самопроизвольно смыкаться. При большем напряжении критическая длина трещины, при которой она является неустойчивой, меньше чем при малом, т. е. = const.

Очагом зарождения трещин являются различные микродефекты:

Хрупкому разрушению металлического монокристалла всегда предшествует местная пластическая деформация, в ходе которой формируются дислокационные микронеоднородности, являющиеся концентраторами внутренних напряжений и вызывав поэтому зарождение и развитие трещины. Происхождение и форма трещины зависят прежде всего от того, с хрупким или пластическим материалом мы имеем дело.

Можно выделить три основных типа разрушения твердых тел.

Первый тип разрушения проявляется, когда дефекты в объеме и на поверхности одинаковы по степени опасности или возникают одновременно в процессе деформирования. Тогда во всем образце одновременно развивается множество микротрещин, которые за тем сливаются в одну магистральную трещину. При этом вся поверхность разрыва образна шероховатая. Так разрушаются поликристаллы, в которых микротрещины возникают в кристаллитах в результате пластической деформации и на ослабленных границах зерен. В монокристаллах множество предразрывных трещин возникает вследствие местных пластических деформаций в различных местах объема.

Второй тип проявляется, когда поверхностные дефекты опаснее внутренних и степень опасности отдельных поверхностных дефектов примерно одинакова. В этом случае при определенных условиях трещины растут единым фронтом кцентру образца. Так разрушаются нехрупкие твердые полимеры при малых напряжениях и больших временах испытаний.

Третий тип разрушения проявляется, когда на поверхности или в объеме хрупкого материала имеется выделяющийся по степени опасности дефект, от которого растет первичная трещина. По мере роста первичной трещины напряжение (σ') в оставшемся неразрушенном сечении образца становится все больше по сравнению с исходным номинальным напряжением, рассчитанным на все поперечное сечение; вследствие этого рост трещины ускоряется. Когда нарастающее напряжение σ' становится равным, а затем превосходит критическое σ_к, происходит переход от первой стадии разрыва ко второй и первичная трещина растет со скоростью, близкой к критической (υ_K). Вторичные трещины начинают быстро расти в оставшемся сечении при . Они образуют шероховатую зону поверхности разрушения, которая покрыта линиями скола, возникающими при встрече фронтов растущих трещин. Третий тип разрушения характерен для таких хрупких, твердых тел, как алмаз, ионные кристаллы, хрупкие пластмассы, керамические материалы, неорганические стекла.

Теоретическая и практическая прочность металлов.

Теоретический расчет прочности кристалла впервые был выполнен Я. Френкелем. В основу была положена простая модель двух рядов атомов, которые смещаются относительно друг друга под действием касательного напряжения т (рис. 5.1). При этом предполагалось, что атомы верхнего ряда перемещаются относительно нижнего как одно целое, одновременно. Такой механизм принято называть схемой жесткого сдвига.

На рис. 5.1. межплоскостное расстояние (расстояние между рядами) принято равным а, а расстояние между атомами в направлении скольжения составляет Ь. Под действием сдвигового напряжения х атомные ряды будут смещаться относительно друг друга, попадая в равновесные позиции в таких точках, как А и В, где напряжение сдвига, необходимое для сохранения данной конфигурации, равно нулю. Это напряжение равно нулю также и в случае, когда в обоих рядах атомы располагаются точно друг над другом в положениях С и D. В промежуточных позициях напряжение имеет какие-то конечные значения, которые периодически меняются в объеме решетки. Если под действием сдвигового напряжения смещение составляет х, то напряжение будет являться периодической функцией х с периодом Ъ. В наиболее простой форме эта зависимость может быть представлена в виде синусоидальной кривой (см. рис. 5.1):
х = ksm(2nx/b). (5.1)

Для малых смещений х = klnx/b. Используя закон Гука, величину напряжения сдвига можно представить в ином виде: т = Gx/a, где G — модуль сдвига; х/а — деформация сдвига.
Если приравнять приведенные выражения для х, то; х = Gb/lmi; подставляя это значение х в соотношение (5.1), получим:
х = ksin(2nx/b)

Для малых смещений х = klnx/b. Используя закон Гука, величину напряжения сдвига можно представить в ином виде: т = Gx/a, где G — модуль сдвига; х/а — деформация сдвига. Дальнейшие расчеты приводить не будем.

Если принять, что а =Ь, тогда теоретическое критическое напряжение сдвига приближенно равно G/2n. Например, для кристаллов меди G = 46 ООО МПа, следовательно, теоретическое значение т = 7320 МПа. В то же время для реальных кристаллов меди наблюдаемое сопротивление сдвигу составляет всего лишь 1,0 МПа. Таким образом, теоретическое значение прочности на несколько порядков выше действительной величины.

Уточнение приведенного выше расчета путем использования более близкого к действительности закона периодического изменения т в зависимости от х приводит к выражению ткр = G/30 (расчет по Маккензи), что также на несколько порядков превышает реальное сопротивление сдвигу.

Аналогичные рассуждения можно провести для случая, когда в результате действия нормальных напряжений происходит одновременный разрыв межатомных связей для двух рядов атомов и образуется трещина. Работа, затрачиваемая на разрушение, расходуется на создание двух новых поверхностей, обладающих поверхностной энергией уг. Теоретическую прочность идеального кристалла, определенную из условия равенства работы отрыва двух рядов атомов и поверхностной энергии, образованной при этом трещины.

Фактическая прочность материалов на несколько порядков меньше значений теоретической прочности. Объяснение расхождения теоретической и реальной прочности материалов дает теория дефектов кристаллического строения, позволившая раскрыть сущность явлений, происходящих при пластической деформации, и установить физическую природу пластичности и прочности металлов и их сплавов.

Остаточные напряжения. Наклёп.

Наклеп - это холодная механическая обработка поверхности, которая заключается в выбрасывании на металлическую деталь дробинок определенного вида и твердости, чтобы ввести на поверхность остаточные напряжения сдавливанием. Упрочнение поверхности металлов и сплавов вследствие изменения их структуры и фазового состава в процессе пластической деформации, при температуре ниже температуры рекристаллизации. Наклёп сопровождается выходом на поверхность образца дефектов кристаллической решётки, увеличением прочности и твёрдости и снижением пластичности, ударной вязкости, сопротивления металлов деформации противоположного знака (эффект Баушингера).

Наклеп на сегодня является широко известной операцией, которая доказала свою необходимость во многих сферах применения, основными принципами которых являются:

Улучшение эксплуатационных качеств деталей, подвергающихся механическим воздействиям глобальным (усталость) или локальным (износ), связанным с агрессивной химической средой (коррозия под напряжением)
Придание формы тонкостенным деталям (наклеп)
Детали, подвергающиеся циклическим напряжениям изгиба или скручивания: пружины подвески (винтовые, листовые), рычаги, поршни, лопасти, валы, зубчатые колеса, торсионы, шпонки, звенья цепей и т.д.
Скорость подачи дроби на деталь 20-120 м/с

· Остаточные напряжения. Классификация

В процессе производства деталей возникают технологические остаточные напряжения. Их появление связано с условиями изготовления деталей.

Виды остаточных напряжений

Остаточные напряжения обычно классифицируют по признакам протяженности силового поля и по физической сущности. Общепринятой является классификация по протяженности силового поля.

Напряжения 1-го рода - макронапряжения. Они охватывают области, соизмеримые с размерами детали, и имеют ориентацию, связанную с формой детали.

Напряжения 2-го рода - микронапряжения, распространяющиеся на отдельные зерна металла или на группу зерен.

Напряжения 3-го рода - субмикроскопические, относящиеся к искажениям атомной решетки кристалла.

Остаточные напряжения l-го рода в материале детали возникают в результате различных технологических факторов при ее изготовлении. Их величина определяется плотностью дислокаций, а знак зависит от характера расположения однородных дислокаций по отношению к поверхности детали. Сжимающие остаточные напряжения возникают в случае преобладающего расположения у поверхности множества положительных дислокаций на параллельных плоскостях скольжения, а в случае рас положения у поверхности отрицательных дислокаций возникают остаточные напряжения растяжения.

По представлению физики твердого тела, напряжения в металле или сплаве рассматриваются как следствие искажения кристаллической решетки. Физической моделью механизма образования технологических остаточных напряжений применительно к деталям, поверхностный слой которых деформирован в процессе механической обработки, в этом случае является атомная или дислокационная модель.

Технологические факторы (способы и режимы обработки поверхности, состояние инструмента, системы и степень охлаждения и др.) оказывают определяющее влияние на величину и знак остаточных напряжений. Обработка резанием (точение) поверхности заготовки детали обычно вызывает появление растягивающих напряжений величиной до 70 МПа. Глубина распространения их находится в пределах 50. 200 мкм и зависит от условий формообразования поверхности. При фрезеровании возникают как растягивающие, так и сжимающие напряжения. При шлифовании чаще всего возникают растягивающие напряжения.

Микронапряжения - местные остаточные напряжения 2-го рода. Они возникают в поликристаллических металлах в процессе деформации больших объемов в результате взаимодействия зерен. К остаточным напряжениям 2-го рода относят также и напряжения внутри отдельного зерна, обусловленные мозаичностью его структуры - результат взаимодействия между отдельными блоками. Эти напряжения являются следствием неоднородности физических свойств различных компонентов поликристалла, а также стесненных условий деформации отдельного зерна и анизотропии свойств внутри его. Основными причинами их возникновения являются фазовые превращения, изменения температуры, анизотропия механических свойств отдельных зерен, границы зерен и распад зерна на фрагменты и блоки при пластической деформации.

Фазовые превращения (в процессе его кристаллизации и остывания, термической обработки и распада твёрдого раствора), сопряженные с увеличением или уменьшением объёма отдельных зерен, порождают значительные остаточные напряжения.

При изменении температуры микронапряжения могут возникать из-за наличия в металле различных компонентов с различными коэффициентами линейного расширения, а также из-за анизотропии свойств отдельных зерен, особенно для металлов с некубической решеткой, обусловливающей различие в величине линейного расширения по разным кристаллографическим осям.

В реальном поликристаллическом металле вместо предполагаемого по расчету равномерного распределения напряжений от действия внешней нагрузки имеет место значительная неравномерность напряжений (деформаций) в отдельных зернах. Неравномерная пластическая деформация обусловливается разницей в модулях упругости различных структурных составляющих, а также неодинаковой способностью деформироваться по разным кристаллографическим осям одного и того же зерна, которая определяется величиной модулей упругости Е и G. В поликристалле, даже при однородном поле напряжений, пластическая деформация распределяется в микрообъемах неравномерно, степень неравномерности при этом достигает 400. 500%. Скопление большого числа дислокаций в граничных слоях вызывает многочисленные искажения атомной решетки, а это создает напряжения 3-го рода. Наряду с этим граничный слой - зона силового взаимодействия между отдельными зернами - создает поле микронапряжений, охватывающих всю поверхность зерна.

Разделение объема зерна на блоки создает в зерне микронапряжения. Причиной возникновения их являются вновь образовавшиеся границы между блоками. В граничном слое между блоками накапливаются дислокации и атомы примесей, которые искажают кристаллическую решетку и порождают напряжения.

Отличие микро- и макронапряжений заключается не только в величине масштаба их проявления. Макронапряжения могут возникать в любой сплошной однородной изотропной среде. Микронапряжения в таком материале существовать не могут, они могут возникать вследствие существенной неоднородности кристаллического материала и его анизотропных свойств.

Возникновение искажений кристаллической решетки связано с отклонением атомов от положения равновесия, причиной которых являются главным образом дислокации и внедренные атомы. Распределение искажений, вызванных присутствием в решетке растворенных атомов, и различного рода несовершенств структуры при низких температурах остается постоянным.

Атомно-кристаллическое строение металлов и сплавов. Дефекты строения. Теоретическая и фактическая прочность.

Под атомно-кристаллической структурой понимают взаимное расположение атомов в кристалле. Кристалл состоит из атомов (ионов), расположенных в определенном порядке, который периодически повторяется в трех измерениях. Наименьший комплекс атомов, который при многократном повторении в пространстве позволяет воспроизвести пространственную кристаллическую решётку, называют элементарной ячейкой.

Рис.2.1. Схема определения координационного числа кристаллической решётки: а – ГЦК; б – ОЦК; в – ГПУ

Простейшим типом кристаллической ячейки является кубическая решётка. В простой кубической решётке атомы расположены (упакованы) недостаточно плотно.

Стремление атомов металла занять места, наиболее близкие друг к другу, приводит к образованию решеток других типов (рис. 2.2):

- объёмноцентрированной кубической решётки (ОЦК) (рис.2.2а) с параметром

а = 0,28 – 0,6мм = 2,8 – 6,0 Å

- гранецентрированной кубической решётки (ГЦК) (рис.2.2б) с параметром

- гексагональной плотно упакованной решётки (ГПУ) (рис.2.2в) с параметром

Рис. 2.2. Кристаллические решётки: а – гранецентрированный куб (ОЦК); б – объемноцентрированный куб (ГЦК); в- гексагональная плотно упакованная (ГПУ)

Узлы (положения атомов), направления в плоскости и в пространстве обозначаются с помощью так называемых индексов Миллера (рис. 2.3). Индексы узла записываются – (mnp), индексы направления - [mnp], индекс плоскости - (hk1).

Рис. 2.3. Символы некоторых важнейших узлов, направлений и плоскостей в кубической решётке

Вследствие неодинаковой плотности атомов в различных плоскостях и направлениях решётки многие свойства отдельно взятого кристалла (химические, физические, механические) по данному направлению отличаются от свойств в другом направлении и, естественно, зависят от того, сколько атомов встречается в этом направлении. Различие свойств в зависимости от направления испытания носит название анизотропии. Все кристаллы анизотропны. Анизотропия – особенность любого кристалла, характерная для кристаллического строения.

Технические металлы являются поликристаллами, т.е. состоят из совокупности кристаллитов с различной ориентацией. При этом свойства во всех направлениях усредняются.

2.2. Дефекты кристаллического строения

Строение реальных кристаллов отличается от идеальных. Реальные кристаллы всегда содержат несовершенства (дефекты) кристаллического строения, которые нарушают связи между атомами и оказывают влияние на свойства металлов.

Дефекты в кристаллах принято классифицировать по характеру их измерения в пространстве:

1. Точечные. Точечными дефектами называются нарушения периодичности кристалла, размеры которых сопоставимы с размерами атома во всех измерениях.

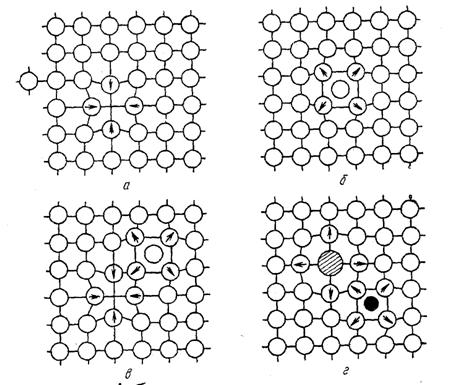
К точечным дефектам относятся вакансии, межузельные атомы, примеси замещения, примеси чужеродных атомов внедрения (рис. 2.5).

Рис. 2.5.Точечные дефекты в кристаллической решетке: а- вакансия;

б - межузельный атом; в- дефект Френкеля; г- примесные атомы замещения (большой) и внедрения (маленький).

Стрелками указаны направления смещений атомов в решетке.

Вакансии и межузельные атомы появляются в кристаллах при любой температуре выше абсолютного нуля из-за тепловых колебаний атомов. Каждой температуре соответствует равновесная концентрация вакансий, а также межузельных атомов. Например, в меди при температуре 20-25 о С содержится 10 -13 ат. % вакансий, а вблизи точки плавления - уже 0,01 ат. % (одна вакансия приходится на 10 4 атомов).

Пересыщение точечными дефектами достигается при резком охлаждении после высокотемпературного нагрева, при пластическом деформировании и при облучении нейтронами. Чем выше температура, тем больше концентрация вакансий и тем чаще они переходят от узла к узлу. Вакансии являются самой важной разновидностью точечных дефектов; они ускоряют все процессы, связанные с перемещениями атомов: диффузию, спекание порошков и т. д.

2. Линейные. Линейные дефекты в кристаллах характеризуются тем, что их поперечные размеры не превышают нескольких межатомных расстояний, а длина может достигать размера кристалла. К линейным дефектам относятся дислокации – линии, вдоль и вблизи которых нарушено правильное периодическое расположение атомных плоскостей кристалла.

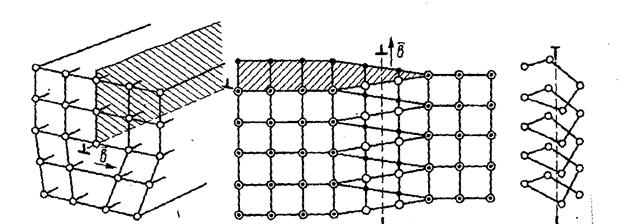
Важнейшие виды линейных несовершенств - краевые и винтовые дислокации (рис.2.6).

Рис. 2.6. Схема дислокаций: а – краевая; б - винтовая

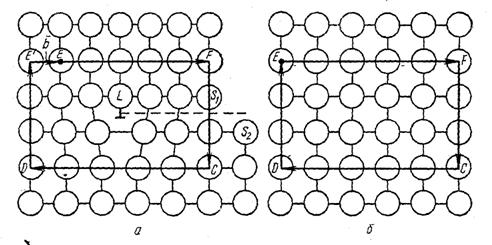
Краевая дислокация в сечении представляет собой край «лишней» полуплоскости в решетке (рис.2.7)

Рис. 2.7. Сечение простой кубической решетки: а - с краевой дислокацией; б - без дислокации.

Вокруг дислокаций решетка упруго искажена. Схема образования атмосферы Коттрелла в кристалле представлена на рисунке 2.8.

Рис. 2.8. Образование атмосферы Коттрелла: а – атомы примеси замещения (заштрихованы) и внедрения беспорядочно расположены в решетке; б, в – атомы примеси переместились к дислокации, в результате чего энергия решетки понизилась.

3. Поверхностные (двумерные). Под этими дефектами понимают нарушения, которые обладают большой протяженностью в двух измерениях и протяженностью лишь в несколько межатомных расстояний в третьем измерении.

К поверхностным дефектам относятся дефекты упаковки, двойниковые границы, границы зерен.

4.Объемные (трехмерные). Под ними понимают нарушения, которые в трех измерениях имеют неограниченные размеры. К таким нарушениям относят трещины, поры, усадочные раковины.

Теоретическая и реальная прочность металла

еоретический расчет прочности кристалла впервые был выполнен Я. Френкелем. В основу была положена простая модель двух рядов атомов, которые смещаются относительно друг друга под действием касательного напряжения т (рис. 5.1). При этом предполагалось, что атомы верхнего ряда перемещаются относительно нижнего как одно целое, одновременно. Такой механизм принято называть схемой жесткого сдвига.

Читайте также: