Сопротивление металлов зависит от

Обновлено: 22.01.2025

К основным свойствам проводниковых материалов относятся:

Удельная проводимость или обратная ей величина – удельное сопротивление;
Температурный коэффициент удельного сопротивления;
Удельная теплопроводность;
Контактная разность потенциалов и термоэлектродвижущая сила;
Предел прочности при растяжении и относительное удлинение при разрыве.

Удельное сопротивление проводников. Величину, обратную удельной проводимости g называют удельным сопротивлением r и для проводника с постоянным поперечным сечением определяют по формуле:

Единицей удельного сопротивления в СИ является Ом×м, однако в практике чаще пользуются внесистемной единицей мкОм×м.

Следует отметить, что в отличие от диэлектриков диапазон удельных сопротивлений металлических проводников достаточно мал – от 0,016мкОм×м. для серебра и примерно до 10 мкОм×м. для железо-хромо-кобальто-алюминиевых сплавов, т.е. занимает всего три порядка.

Температурная зависимость удельного сопротивления металлических проводников. Как было показано ранее в идеально чистых металлах единственной причиной, которая ограничивает длину свободного пробега, являются тепловые колебания узлов кристаллической решетки (фононы). Удельное сопротивление металла, обусловленное этим фактором, обозначим как ρ_Т_.. С ростом температуры возрастают амплитуды фононов и связанные с этим флюктуации периодического поля решетки. Это повышает рассеивание электронов, уменьшает длину свободного пробега и вызывает возрастание удельного сопротивления. Для упрощенной одномерной модели решетки длина свободного пробега электронов определяется как:

где λ_св - длина свободного пробега;

Δa - амплитуда фононов;

N - концентрация атомов в металле.

Потенциальная энергия атома, отклоненного на Δa от узла решетки:

где К_упр - коэффициент упругости связи.

Согласно классической статистике средняя энергия одномерного гармоничного осциллятора равняется КТ. Тогда:

½ · K_упр (Δa) 2 = КТ (4.6)

где К - постоянная Больцмана.

Тогда из (4.5), (4.6) получим:

Если подставить (4.7) в (4.2) получим:

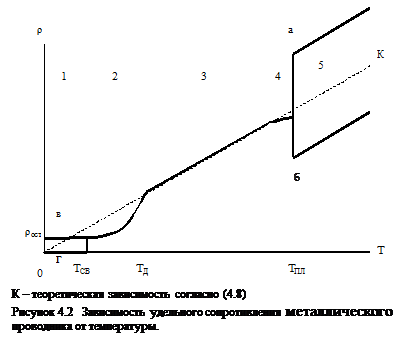
То есть с ростом температуры удельное сопротивление чистых металлов должно возрастать линейно. В действительности эта зависимость является более сложной (рисунок 4.2)

На участке 3 при комнатных температурах зависимость ρ = ¦(Т) линейна, как это видно из (4.8). То есть с ростом температуры возрастает амплитуда тепловых колебаний узлов кристаллической решетки, что уменьшает длину свободного пробега электронов.

На участке 4 вблизи температуры плавления имеет некоторая нелинейность, что объясняется другими механизмами рассеивания электронов.

При переходе металла из твердого состояния в жидкое (температура плавления Т_пл) может иметь место как резкое возрастание удельного сопротивления (а), так и его уменьшение (б). Это связано с изменением структуры кристаллической решетки. Если при плавлении объем металла возрастает, что имеет место для большинства металлов, то расстояние между атомами тоже возрастает, металлическая связь уменьшается, а амплитуда фононов возрастает, что уменьшает длину свободного пробега электронов, следовательно, сопротивление металла возрастает. Для некоторых металлов (висмут, галлий) при плавлении объем металла уменьшается, что усиливает связи между атомами, амплитуда фононов уменьшается и удельное сопротивление тоже уменьшается.

На участке 5 металлы находятся в жидком состоянии и сохраняют кристаллическую решетку, поэтому зависимость удельного сопротивления от температуры поясняется аналогично участку 3.

На участке 2, ниже температуры Дебая (Т_Д) изменяется частота тепловых колебаний узлов кристаллической решетки, поэтому зависимость ρ = ¦(Т) нелинейна и подчиняется закону:

ρ = A·T n (4.9)

где n - изменяется от 1 до 5.

На участке 1 некоторые металлы имеют конечное сопротивление (r_ост) даже при температуре Т=0 К. Это объясняется наличием в металле статических дефектов решетки, прежде всего примесей. Это позволяет оценивать чистоту металлов на основании отношения:

где ρ_300K , ρ_4K - соответственно удельное сопротивление металла при 300 К и 4,2 К (температура кипения жидкого гелия). Чем меньше это отношение, тем чище металл.

У некоторых металлов при температуре ниже Т_св наблюдается резкое уменьшение удельного сопротивления до нуля. Такое явление называют сверхпроводимостью.

Таким образом, согласно (4.9) металлические проводники в обычных условиях имеют линейную зависимость удельного сопротивления от температуры.

Влияние примесей на удельное сопротивление металлических проводников.Как уже говорилось, причинами рассеяния электронов в металлах являются не только тепловые колебания узлов кристаллической решетки, но и наличие статических дефектов, которые, прежде всего связанные с примесями. Рассеивание на статических дефектах не зависит от температуры. Поэтому при абсолютном нуле сопротивление реальных металлов остается конечным. Из этого следует правило Маттиссена об аддитивности удельного сопротивления:

где ρ_пр - полное сопротивление металла с примесью;

ρ_т - сопротивление, обусловленное рассеянием электронов на фононах;

ρ_ост - остаточное сопротивление, обусловленное рассеиванием электронов на статических дефектах решетки.

Наибольший вклад в остаточное сопротивление вносит рассеяние на примесных атомах, которые практически всегда имеются в металлах. Поэтому длина свободного пробега электронов в металлах с примесью состоит из:

где l_Т, l_Д - длина свободного пробега электронов, ограниченная фононами и примесями, соответственно.

Длина пробега l_Д:

где N_d - концентрация атомов примеси;

S_d – эффективная плоскость рассеивания электронов атомами примеси.

Тогда удельное сопротивление проводника с примесью:

То есть наличие примесь увеличивает удельное сопротивление металла, но его зависимости от температуры остается линейной (рис. 4.3)

Dρ_ост = а +b(DZ) 2 (4.14)

где Dρ_ост - изменение остаточного сопротивления при изменении примеси;

DZ - разность валентностей собственного атома и атома примеси;

а, b - константы.

Таким образом, на сопротивление металлов меньшее влияние оказывают примесные атомы металла, а большее – атомы металлоидов.

В технике очень широко используют металлические сплавы, имеющие значительную концентрацию атомов примеси, со структурой неупорядоченного твердого раствора. Статическое распределение атомов разного вида в узлах кристаллической решетки вызывает значительные флюктуации периодического поля кристалла, рассеивающего электроны. Но в неупорядоченных твердых растворах, преимущественно с добавкой примеси, изменяется только период решетки. Поэтому действителен закон Нордгейма:

де С - константа;

x_А, x_В - атомные доли компонентов в сплаве.

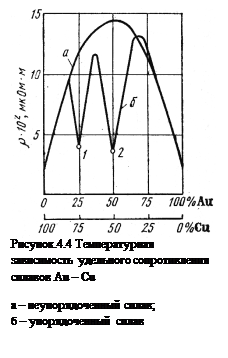
То есть в бинарных твердых растворах А-В остаточное сопротивление возрастает, как при добавлении атомов металла В к металлу А, так и при добавленные атомов металла А к металлу В (рис. 4.4). Остаточное сопротивление достигает максимума при x_А = x_В = 0,5.

Закон Нордгейма описывает изменение остаточного сопротивления для непрерывных неупорядоченных твердых растворов. Если сплав отжечь, то он может стать упорядоченным и, если при этом возникают интерметаллические соединения, которые имеют собственную кристаллическую решетку, то зависимость остаточного сопротивления разделяется на части, соответственно числу интерметаллических соединений. Таким образом, удельное сопротивление металлических сплавов всегда выше сопротивления чистых металлов. Это свойство используется для получения высокоомных проводниковых материалов.

Изменение удельного сопротивления при упругих деформациях объясняется изменением амплитуды колебания узлов кристаллической решетки металла. Увеличение амплитуды колебания узлов решетки металла приводит к уменьшению длины свободного пробега носителей заряда и удельное сопротивление возрастает. Пластическая деформация, как правило, повышает удельное сопротивление металлов вследствие искажения кристаллической решетки. При рекристаллизации путем термической обработки (отжига) удельное сопротивление может вновь снижено до первоначальных значений.

Температурный коэффициент удельного сопротивления.В диапазоне температуры, где зависимость r от t близка к линейной (рис. 4.2, участок 3) допустима линейно-кусочная аппроксимация этой зависимости, и величина удельного сопротивления в конце диапазона температуры t может быть подсчитана по формуле

где r₀—удельное сопротивление в начале диапазона.

Величину a_r из выражения (4.) называют средним температурным коэффициентом удельного сопротивления в данном диапазоне температуры:

Дифференциальное выражение для a_r имеет вид

Значения a_r чистых металлов в твердом состоянии близки друг к другу, и поэтому приближенно можно считать a_r » 0,004 , К -1 .

Исключение составляют элементы, относящиеся к ферромагнетикам — железо, никель, кобальт, гадолиний, а также натрий, калий, хром и др., однако и для них a_r отличается от приведенной величины только в 1,5—2 раза.

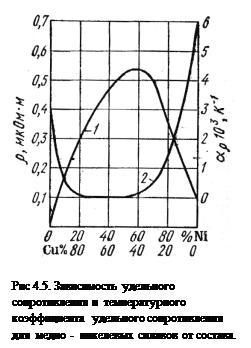
Наличие примесей уменьшает значение α_ρ. У некоторых сплавов α_ρ. даже может приобретать небольшие отрицательные значения (рис.4.5). Это объясняют тем, что при более сложных составе и структурax по сравнению с чистыми металлами сплавы нельзя рассматривать как классические металлы, т. е. изменение проводимости их обусловливается не только изменением подвижности носителей заряда но в некоторых случаях и частичным возрастанием концентрации носителей при повышении температуры. Сплав, у которого уменьшение подвижности с увеличением температуры компенсируется возрастанием концентрации носителей заряда, имеет нулевой температурный коэффициент удельного сопротивления.

Это явление используется для изготовления термостабильных сплавов, например, константана, манганина ). Константан - сплав с 60% Ni и 40% Сu имеет большое сопротивление (~0,5 мкОм×м) и очень малый температурный коэффициент (меньше 10 -6 К -1 ), отсюда и его название.

Удельная теплопроводность металлов. Высокая теплопроводность металлов легко объясняется посредством передачи тепловой энергии атомов нагретого участка металла атомам холодного участка за счет переноса этой энергии коллективизированными электронами. Так как механизм электропроводности и теплопроводности в металлах обусловлен одними и теми же факторами: движением электронного газа и его плотностью, очевидно, что металлы с высокой электропроводностью являются также хорошими проводниками тепла, а диэлектрики обладают не только низкой электропроводностью, но и низкой теплопроводностью. Так, медь имеет удельную теплопроводность 406 Вт/К×м, серебро 453 Вт/К×м, алюминий 218 Вт/К×м, что значительно выше чем у диэлектриков. Удельная теплопроводность и электропроводность металлов связаны законом Видемана-Франца:

где l_Т - удельная теплопроводность.

σ - удельная электропроводность.

L₀ - число Лоренца.

Поскольку на участке комнатных температур удельная электропроводность падает пропорционально температуре, то согласно (4.19), удельная теплопроводность металлов не должна зависеть от температуры. Это следствие из закона Видемана-Франца выполняется для большинства металлов. Это свойство применяют в технике, при использовании металлов как радиаторов для охлаждения мощных полупроводниковых приборов.

Для этой цели необходимо использовать металлы с большим значением удельной теплопроводности. Чаще всего, это сплавы на основе алюминия (силумин), которые имеют хорошие тепловые, механические и антикоррозийные свойства. Медь нельзя использовать вследствие её плохой коррозионной стойкости, а серебро - вследствие высокой стоимости.

Контактные явления и термоэлектродвижущая сила (термо-э.д.с.)

При соприкосновении двух разных металлов, между ними возникает контактная разность потенциалов. Согласно квантовой теории причиной этого является различная энергия Ферми соприкасающихся металлов. Пусть в изолированном состоянии электронный газ в металлах А и В имеет энергию Ферми W_F A и W_F B , отсчитываемую от дна зоны проводимости (рис.4.6).

Термодинамическая работа выхода электронов из металла равняется, соответственно, c_А и c_В_. Поскольку кинетическая энергия электронов, которые находятся на уровне Ферми в разных металлах различна, то при контакте материалов возникает значительный переход электронов из металла В с большим значением энергии Ферми в металл, где эта энергия меньше. Например, из металла В в металл А. Вследствие этого металл В заряжается положительно, а металл А - отрицательно. Между ними возникает разность потенциалов, которая блокирует дальнейший переход носителей заряда. Равновесие наступит, если:

где U_K - контактная разность потенциалов.

контактная разность потенциалов достигает несколько вольт.

Термоэлемент, который построен из двух различных металлических проводников с замкнутой цепью, называют термопарой (рис.4.7).

Вольтметр в такой цепи будет показывать разность потенциалов, которую называют термоэлектродвижущей силой (термо-э.д.с.). Термо-э.д.с. равняется:

где a_T — относительная удельная термо-э.д.с.

Значение a_T зависит от природы материалов и температуры и включает в себя три составляющих. Первая обусловлена температурной зависимостью контактной разности потенциалов, поскольку с ростом температуры уровень Ферми в металлах незначительно, но смещается.

Вторая составляющая обусловлена диффузией носителей заряда от горячих спаев к холодным. Поскольку существует градиент температуры от контакта к контакту, то возникает диффузия электронов от горячего контакта к холодному, что дает некоторый вклад в возникающую разность потенциалов.

Третья составляющая возникает вследствие захвата электронов квантами тепловой энергии. Их поток тоже передвигается к холодному контакту. Значение a_T приблизительно равняется нескольким мкВ/К.

Термопары часто используют для измерения температуры. Если температуру холодного контакта поддерживать 0 О С, то вольтметр будет показывать напряжение пропорциональное температуре горячего контакта. Достоинством термопар является высокая линейность, возможность измерения температуры в широком интервале температур, независимость значения термо-э.д.с. от длины проводников.

Вследствие того, что значение a_T зависит от состава материала и незначительно от температуры, термопары градуируют, используя точки плавления металлов: свинца, олова, серебра и других.

Наиболее распространенными термопарами являются:

· Хромель- копель (типа ХК). Она позволяет измерять температуры до 600 О С и имеет при этой температуре термо-э.д.с. приблизительно 50 мВ.

· Хромель-алюмель (типа ХА). Она используется к температурам 1000 О С и имеет при этой температуре термо-э.д.с. приблизительно 40 мВ.

· Медь-константан. Ее используют при низких температурах до 350 О С. При этой температуре термо-э.д.с. достигает 15 мВ.

· Платинородий-платина (типа ПП или ППР). Ее применяют до температуры 71600 О С. Термо-э.д.с. у этой термопары невелика (приблизительно 14 мВ при 1600 О С). Но она позволяет обеспечить наиболее точные и стабильные измерения температуры.

Однако явление термо-э.д.с. имеет и отрицательные стороны. В реальных условиях исключить градиенты температур практически невозможно. Поэтому, если контактируют различные металлы, то возможно возникновение паразитной термо-э.д.с. Для устранения этого в цепях (прежде всего электроизмерительных устройств), надо подбирать контактирующие металлы с малыми значениями термо-э.д.с. Такой парой, например, является медь-манганин.

от чего зависит сопротивление металов? и как оно выражается?

Электри́ческое сопротивле́ние - скалярная физическая величина, характеризующая свойства проводника и равная отношению напряжения на концах проводника к силе электрического тока, протекающему по нему.

В международной системе единиц (СИ) единицей сопротивления является ом (Ω, Ом) . В системе СГС единица сопротивления не имеет специального названия. Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно определить как

где
R — сопротивление;
U — разность электрических потенциалов на концах проводника, измеряется в вольтах;
I — ток, протекающий между концами проводника под действием разности потенциалов, измеряется в амперах.

Обратной величиной по отношению к сопротивлению является электропроводность, единицей измерения которой служит сименс.

Высокая электропроводность металлов связана с тем, что в них имеется громадное количество носителей тока — электронов проводимости, образующихся из валентных электронов атомов металла, которые не принадлежат определённому атому. Электрический ток в металле возникает под действием внешнего электрического поля, которое вызывает упорядоченное движение электронов. Движущиеся под действием поля электроны рассеиваются на неоднородностях ионной решётки (на примесях, дефектах решётки, а также нарушениях периодической структуры, связанной с тепловыми колебаниями ионов) . При этом электроны теряют импульс, а энергия их движения преобразуются во внутреннюю энергию кристаллической решётки, что и приводит к нагреванию проводника при прохождении по нему электрического тока.

В других средах (полупроводниках, изоляторах, электролитах, неполярных жидкостях, газах и т. д. ) в зависимости от природы носителей заряда физическая причина сопротивления может быть иной. Линейная зависимость, выраженная законом Ома, соблюдается не во всех случаях.

Сопротивление проводника при прочих равных условиях зависит от его геометрии и от удельного электрического сопротивления материала, из которого он состоит.

Сопротивление однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины, сечения и вычисляется по формуле:

где ρ — удельное сопротивление вещества проводника, L — длина проводника, а S — площадь сечения.

Удельное сопротивление — скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника единичной длины и единичной площади.

Сопротивление металлов снижается при понижении температуры; при температурах порядка нескольких кельвинов сопротивление большинства металлов и сплавов стремится или становится равным нулю (эффект сверхпроводимости) . Напротив, сопротивление полупроводников и изоляторов при снижении температуры растёт. Сопротивление также меняется по мере увеличения тока/напряжения, протекающего через проводник/полупроводник.

Физика. 10 класс

§ 34. Электрический ток в металлах. Сверхпроводимость

Типичными представителями класса проводников являются металлы. Какова природа электрического тока в металлах?

Природа электрического тока в металлах. В металлических проводниках носители электрического заряда — свободные электроны. Под действием внешнего электрического поля свободные электроны упорядоченно движутся, создавая электрический ток ( рис. 194 ).

Электронная проводимость металлов была впервые экспериментально подтверждена немецким физиком К. Рикке ( 1845–1915 ) в 1901 г. Суть опыта Рикке заключалась в следующем: по проводнику, состоявшему из трёх отполированных и плотно прижатых друг к другу цилиндров — двух медных и одного алюминиевого ( рис. 195 ), в течение года проходил ток одного и того же направления. За этот промежуток времени через проводник прошёл заряд более 3,5 МКл. После завершения опыта взвешивание показало, что массы цилиндров остались неизменными. Это явилось экспериментальным доказательством того, что перенос заряда при прохождении тока в металлах не сопровождается химическими процессами и переносом вещества, а осуществляется частицами, которые являются одинаковыми для всех металлов, т. е. электронами.

В 1916 г. американский физик Р. Толмен ( 1881—1948 ) и шотландский физик Т. Стюарт усовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением свободных электронов.

В этих опытах катушку с большим числом витков тонкой проволоки подключали к гальванометру и приводили в быстрое вращение вокруг своей оси ( рис. 195.1 ). При резком торможении катушки в цепи возникал кратковременный ток, обусловленный инерцией носителей заряда. По направлению отклонения стрелки гальванометра было установлено, что электрический ток создают отрицательно заряженные частицы. При этом экспериментально полученное отношение заряда каждой из этих частиц к её массе (удельный заряд) близко к удельному заряду электрона, полученному из других опытов. Так было экспериментально доказано, что носителями свободных зарядов в металлах являются электроны.

Вещества, обладающие электронной проводимостью, называют проводниками первого рода.

В соответствии с классической электронной теорией проводимости металлов, созданной немецким физиком П. Друде ( 1863–1906 ) в 1900 г., металлический проводник можно рассматривать как физическую систему, состоящую из свободных электронов и положительно заряженных ионов, колеблющихся около положений равновесия ( рис. 196 ).

Появление свободных электронов при образовании металлического кристалла из нейтральных атомов можно упрощённо объяснить следующим образом. Электроны, находящиеся на внешних оболочках атомов, слабо связаны со своими ядрами. При образовании кристалла атомы сближаются на расстояние r 0,1 нм , и электроны начинают взаимодействовать не только со своими ядрами, но и с ядрами соседних атомов. В результате этого их взаимодействие с собственными ядрами значительно ослабевает, вследствие чего они теряют с ними связь и могут двигаться по всему кристаллу в любом направлении как свободные частицы. Атомы превращаются при этом в положительно заряженные ионы. В пространстве между ионами беспорядочно движутся подобно частицам идеального газа свободные электроны. Поэтому для описания движения электронов используют модель «электронный газ» — совокупность свободных электронов в кристаллической решётке металла. На рисунке 196.1 пунктирной линией изображена траектория движения одного из электронов.

В этой модели электроны, упорядоченное движение которых является током проводимости, рассматривают как материальные точки, модуль потенциальной энергии взаимодействия которых пренебрежимо мал по сравнению с их кинетической энергией. Считают, что движение электронов под действием электрического поля подчиняется законам классической механики, а их столкновения с ионами кристаллической решётки металла являются неупругими, т. е. при столкновениях электроны полностью передают ионам кинетическую энергию своего упорядоченного движения. В промежутках между столкновениями свободные электроны совершают беспорядочное тепловое движение и в то же время движутся упорядоченно и равноускоренно под воздействием электрического поля.

Интересно знать

Модель электронного газа позволяет теоретически объяснить природу сопротивления и обосновать закон Ома для участка цепи, не содержащего источника тока, на основе классической электронной теории проводимости металлов. Проанализируем упорядоченное движение электронов проводимости.

Пусть электрон движется с ускорением в направлении, противоположном направлению напряжённости электрического поля ( рис. 196.2 ): где m₀ — масса электрона, e — элементарный электрический заряд (модуль заряда электрона).

Тогда модуль средней скорости его направленного движения: , где — усреднённый промежуток времени между двумя последовательными столкновениями электрона с ионами кристаллической решётки.

Поскольку электрическое поле внутри однородного прямолинейного проводника с током однородное, то модуль напряжённости этого поля где l — длина проводника, U — напряжение между его концами. Тогда модуль средней скорости направленного движения электронов пропорционален напряжению между концами проводника .

Сила тока в проводнике пропорциональна модулю средней скорости направленного движения электронов:

где q — модуль заряда электронов проводимости, находящихся в проводнике, — усреднённое время прохождения этих электронов по проводнику, N — количество электронов проводимости в проводнике, n — концентрация этих электронов, V = Sl — объём проводника. Следовательно, сила тока пропорциональна напряжению между концами проводника I U.

Электрическое сопротивление металлов. Сверхпроводимость

1. Электрическое сопротивление металлов. Квантовая теория электропроводности металлов сводится к следующему:

а. В идеальной кристаллической решетке электроны проводимости при своем движении не должны испытывать сопротивления. Сопротивление возникает тогда, когда в решетке появляются дефекты структуры, то есть нарушается периодичность решетки.

б. В реальных кристаллах есть два механизма нарушения структуры: примесный и тепловой. Соответственно различают примесное удельное сопротивление r_n и тепловое (колебательное) r_Т. Согласно правилу аддитивности сопротивлений полное сопротивление металла r равно их сумме, r = r_n + r_Т. (13.1)

в. Примесное сопротивление r_n обусловлено наличием инородных атомов в решетке (атомов примеси). Если металл достаточно чистый и концентрация атомов примеси невелика, то примесное сопротивление практически не зависит от температуры и становиться заметным лишь вблизи абсолютного нуля. Благодаря примеси удельное сопротивление металла не должно обращаться в нуль даже при Т = 0 К.

г. Тепловое сопротивление r_Т возникает благодаря рассеянию электронов проводимости на флуктуациях плотности узлов кристаллической решетки, возникающих при тепловом колебательном движении узлов. В квантовой теории тепловое колебательное движение атомов решетки трактуется как система стоячих звуковых волн в кристалле - фононов. Поэтому говорят о рассеянии электронов проводимости на фононах.

В отличие от классической теории электропроводности металлов Друде - Лоренца, прогнозирующей зависимость сопротивления от температуры вида r ~ , квантовая теория дает правильный прогноз линейной зависимости r ~Т. При температурах металла Т ³ 50 К r = r₀aТ, что соответствует эмпирической формуле r = r₀(1 + a t). В квантовой теории получается, что при Т ® 0 полное удельное сопротивление металла r должно стремиться к примесному r_n. На рис.90 показана опытная зависимость удельного сопротивления чистого натрия от температуры.

При Т ® 0 К r ® r_n = 4·10 -11 Ом·м, что составляет примерно 0,4% от сопротивления при Т = 273 К. Уже при температурах Т ³ 20 К зависимость r(Т) становится практически линейной.

д. Электрический ток толкуется в квантовой теории как дрейф электронов в периодическом поле кристалла. Этот дрейф происходит под действием постоянной электрической силы еЕ, где Е- напряженность электрического поля, создающего ток. Оказалось, что скорость дрейфа электронов зависит от глубины их положения в зоне проводимости. Эта зависимость выражается через эффективную массу m_эф электрона. В отличие от массы покоя m_е свободного электрона эффективная масса электрона в зоне проводимости металла – величина переменная, зависящая от ширины зоны.

Вблизи дна зоны эффективная масса электронов положительна. Направление дрейфа соответствует вектору плотности тока. По мере подъема к верхней границе зоны эффективная масса принимает бесконечно большое значение m_эф = ¥, а затем становится отрицательной. Соответственно и скорость дрейфа электронов, имея “правильное” направление у дна зоны, постепенно проходит через нуль и принимает отрицательные (“неправильные”) значения у верхней границы зоны.

Соотношения, полученные в приближении свободных электронов в теории Друде – Лоренца, оказываются справедливыми для электронов, движущихся в периодическом поле решетки, если в них заменить массу покоя электрона m_е на эффективную m_эф.

2. Сверхпроводимость. В 1911 году Камерлинг – Оннес, измеряя сопротивление ртути в области низких температур, обнаружил, что при Т = 4,2 К сопротивление ртути практически падало до нуля. Это явление стали называть сверхпроводимостью. На рис.91 показаны опытные кривые зависимости удельного сопротивления некоторых чистых металлов от температуры вблизи абсолютного нуля. Очевидно, что явление не сводится к нормальному падению удельного сопротивления бездефектного кристалла, когда r_n = 0, и r_Т . Переход в сверхпроводящее состояние происходит не плавно, а скачкообразно при некоторой температуре Т_кр, которую называют критической температурой перехода. Сейчас известно около 30 сверхпроводящих химических элементов и свыше 500 сверхпроводящих материалов.

3. Эффекты сверхпроводимости.

а. Электрический ток, возбужденный в сверхпроводящем кольце, может циркулировать в нем годами.

б. ЭффектМейснера. В 1933 году Вальтер Мейсснер и Р. Оксенфельд обнаружили, что вещество, помещенное в магнитное поле (рис.92 слева), при переходе в сверхпроводящее состояние не замораживает находящееся в нем магнитное поле, как это должно было быть при простом переходе вещества в состояние с нулевым сопротивлением, а выталкивает его из своего объема (рис. 92 справа). Это присуще идеальным диамагнетикам с нулевой магнитной проницаемостью m = 0.

Из того, что магнитное поле не проникает в сверхпроводник, следует, что электрический ток может течь лишь по поверхности сверхпроводника. Ведь если бы ток мог протекать в толще сверхпроводника, то вокруг него в толще сверхпроводника было бы магнитное поле. И действительно, опыт показывает, что электрический ток течет в сверхпроводнике в поверхностном слое толщиной l = 10 ¸ 100 нм. На эту глубину в сверхпроводник проникает и магнитное поле, убывая с расстоянием x от поверхности по экспоненциальному закону

В = В₀exp(-xçl). (13.2)

Вещество в сверхпроводящем состоянии приобретает два не связанных друг с другом фундаментальных свойства: идеальную проводимость и идеальный диамагнетизм.

Эффект Мейснера позволяет устойчиво подвешивать сверхпроводящие тела в магнитном поле (рис.93). При пререходе шара в сверхпроводящее состояние 1-го рода магнитное поле из него вытесняется. В результате в поверхностном слое шара индуцируется ток такого направления, при котором шар выталкивается из поля.

в. Эффект критического магнитного поля. Он состоит в том, что при достижении магнитным полем, в котором находится сверхпроводник, некоторого предельного значенияиндукции В_кр »10 -2 ¸ 10 1 Тл, сверхпроводимость исчезает.

На рис.94 показана зависимость В_кр от температуры для свинца (верхняя кривая) и для олова (нижняя кривая). При критической температуре Т = Т_кр критическое поле равно нулю, В_кр = 0, а с понижением температуры В_кр увеличивается.

Если усиливать ток, идущий по сверхпроводнику, то при некотором его критическом значении I_кр сверхпроводящее состояние разрушается. Поскольку магнитное поле В пропорционально току I, то зависимость I_кр от температуры аналогична зависимости В_кр(Т). Эффект критического магнитного поля усложняет технику получения сверхсильных магнитных полей с помощью сверхпроводящих контуров. Расчет критического тока должен учитывать, что ток течет в приповерхностном слое. Например, у проводника диаметром 1 мм при l = 35 нм сечение приповерхностного слоя, по которому течет ток, около 10 -4 мм 2 . Это составляет около 0,01% всего сечения проводника.

г. Эффект Джозефсона. В 1962 году Брайан Джозефсон теоретически предсказал два эффекта, суть которых в следующем.

Подсоединим к сверхпроводнику (на рис.95-а он изображен в виде бруска) амперметр А с источником постоянного тока, ЭДС которого E, и вольтметр V. В цепи идёт постоянный ток, регистрируемый амперметром. Так как сопротивление сверхпроводника равно нулю, то вольтметр показывает нуль.

Разрежем сверхпроводник на две части и раздвинем их, чтобы между ними возник зазор толщиной d » 1 нм. Как предсказал Джозефсон, при включении такого сверхпроводника в цепь может наблюдаться один из следующих двух эффектов.

Стационарный эффект Джозефсона. Через сверхпроводник по-прежнему идёт постоянный ток. Оказывается, ток может течь без сопротивления не только через сверхпроводник, но и через щель в нем, если она достаточно узка (рис.95-б).

Нестационарный эффект Джозефсона. На концах сверхпроводника со щелью может возникнуть постоянная разность потенциалов. В этом случае из щели излучается высокочастотная электромагнитная волна (рис.95-в). Через сверхпроводник течет не только постоянный, но и высокочастотный переменный ток.

В настоящее время эффекты Джозефсона не только подтверждены экспериментально, но и используются в микроэлектронике.

4. Теорию сверхпроводимости построили в 1957г Джон Бардин, Леон Купер и Джон Шриффер. По первым буквам их фамилий ее назвали БКШ – теорией. В основе БКШ- теории лежит представление, что между электронами проводимости металла могут действовать силы притяжения, возникающие вследствие поляризации ими кристаллической решетки.

Электрон, движущийся в решетке, притягивает к себе положительно заряженные ионы, несколько сближая их, и тем самым создает вдоль пути своего следования избыточный положительный заряд поляризованной решетки, к которому могут быть притянуты другие электроны. Это эквивалентно возникновению силы притяжения между электронами, только действующей не непосредственно, а через поляризованную решетку.

Можно предположить, что сверхпроводимость следует ожидать прежде всего у тех металлов, у которых имеет место сильное взаимодействие электронного газа с решеткой, приводящее в обычных условиях к высокому удельному сопротивлению. И действительно, из чистых металлов лучшими сверхпроводниками оказались наиболее высокоомные - свинец Рb, ниобий Nb, олово Sn, ртуть Hg. В то же время у таких низкоомных металлов, как медь Cuи сереброAg, у которых электронный газ имеет высокую подвижность, сверхпроводимость не наблюдается.

Как показал Леон Купер, при Т < Т_кр, самые верхние электроны,расположенные на уровне Ферми, могут спариваться. При этом их суммарная энергия оказывается меньше суммы энергий отдельных электронов. Выделяющаяся энергия должна отводиться от кристалла охлаждением. Понижение энергии куперовских пар приводит к понижению верхнего занятого электронами уровня. В результате между уровнями куперовских пар и ближайшими свободными уровнями возникает запрещенная зона шириной 2D (рис.96 слева). Эта возникшая энергетическая щель не позволяет куперовским парам электронов принимать малую энергию. Они могут принять лишь энергию не менее 2D, которая позволит электронам перепрыгнуть через эту щель. Поэтому при Т < Т_кр куперовские пары оказываются весьма устойчивыми.

При Т < Т_кр спариваются не все электроны. При каждой температуре устанавливается некоторое равновесное соотношение между концентрациями нормальных и спаренных электронов. Оказывается, что ширина 2D энергетической щели в сверхпроводнике зависит от количества неспаренных электронов. Их концентрация понижается с уменьшением температуры и соответственно растет ширина щели (рис.96 справа).

Электроны, образующие куперовские пары, имеют противоположные спины. Поэтому спин пары равен нулю, и она представляет собой бозон. Бозоны могут накапливаться в основном энергетическом состоянии, из которого их трудно перевести в возбужденное состояние. Поэтому куперовские пары в состоянии согласованного движения могут оставаться неопределенно долго. Такое согласованное движение пар и есть ток сверхпроводимости.

Расстояние между электронами пары велико. Оно составляет примерно 1000 нм, что около 5000 поперечников атомов. Примерно 1000 пар перекрываются, занимая общий объем.

5. Объяснение БКШ – теорией эффекта критического тока. У известных сверхпроводников величина энергетической щели составляет в среднем 2D = 3 мэВ » 5·10 -22 Дж. Для разрушения куперовской пары один из электронов пары должен уменьшить энергию своего движения, по крайней мере, на величину 2D.

Предположим, что электрон отдает эту энергию при лобовом столкновении с узлом решетки так, что после столкновения он отскакивает с той же скоростью дрейфа v_д в обратном направлении. Энергия электрона до соударения Е_к1 = m_e(v_ф + v_д) 2 ç2, энергия после соударения Е_к2 = m_e(v_ф - v_д) 2 ç2. Здесь v_ф – тепловая скорость электронов на уровне Ферми (»10 6 мçс), v_д – скорость дрейфа электронов в электрическом поле, она не превышает 1 мçс.

Убыль кинетической энергии электрона должна быть по крайней мере равной 2D. Так что DЕ_к= = 2m_ev_фv_д = 2D. (13.3)

Отсюда, минимальная скорость дрейфа v_д, необходимая для разрушения куперовской пары, есть v_д = Dçm_ev_ф. (13.4)

Плотность электронного тока проводимости естьj = env_д, (13.5)

где n – концентрация электронов проводимости в металле. Подставив критическую скорость дрейфа из (13.4), получаем критическую плотность тока j_кр.

У типичных сверхпроводников n = 3·10 28 м -3 , v_ф = 10 6 мçс, 2D = 3 мэВ. Подставляем.

j_кр = =10 12 . Это соответствует току 10 6 А через проводник сечением 1 мм 2 . Но в реальном сверхпроводнике ток течет лишь в тонком приповерхностном слое толщиной около 35 нм, что соответствует сечению S = 10 -4 мм 2 . Поэтому критический ток в сверхпроводнике толщиной около 1 мм составляет всего лишь i_кр = j_крS = 10 6 Аçмм 2 ·10 - 4 мм 2 = 100 А. Это вполне соответствует эксперименту.

6. Объяснение БКШ-теорией критического магнитного поля. При помещении сверхпроводника в магнитное поле В в поверхностном слое сверхпроводника наводится незатухающий ток. Этот незатухающий ток имеет такие величину и направление, что его магнитное поле внутри сверхпроводника полностью компенсирует внешнее поле В. При увеличении поля В плотность компенсирующего тока в сверхпроводнике растет. Если внешнее поле В будет настолько большим, что плотность наведенного им индукционного тока достигнет критического значения, сверхпроводимость разрушается.

Все выше сказанное относится к сверхпроводникам 1-го рода, в которых электрический ток существует только в приповерхностном слое. Несколько позже были открыты и изучены сверхпроводники 2-го рода. В них возникающие во внешнем магнитном поле В сверхпроводящие токи текут не только по поверхности, но и проникают в толщу проводника. У сверхпроводников 1-го рода критическое магнитное поле В_кр не превышает 0,1 Тл, а у сверхпроводников 2-го рода достигает величины В_кр» 20 Тл.

7. Эффекты Джозефсона объясняются БКШ - теорией как результат туннелирования куперовских пар через узкую щель между сверхпроводниками. Согласно теории, частота n переменного сверхпроводящего тока определяется выражением: n = . (13.7)

При напряжении на щели U = 1 мВ частота n = 485 ГГц, что соответствует длине волны ЭМ излучения l = сçn = 0,6 мм.

8. Реактивное сопротивление сверхпроводника. При любой температуре Т < Т_кр сверхпроводник практически всегда содержит как сверхпроводящие электроны концентрацией n_c, так и нормальные (n_н) электроны. Если поместить сверхпроводник в высокочастотное поле, то в этом переменном электрическом поле ускоряются не только куперовские пары, но и нормальные электроны. Поэтому ток имеет как сверхпроводящую, так и нормальную составляющую.

Те и другие электроны обладают массой, вследствие их инерции ток отстает по фазе от напряженности ВЧ – поля. Куперовские пары движутся в проводнике как бы без трения. Согласно классической механике, скорость частиц в этом случае отстает по фазе от действующей на них периодической силы на pç2. Поэтому сверхпроводящая составляющая высокочастотного тока отстает от напряженности поля на pç2. Это значит, что куперовские пары создают чисто реактивное сопротивление.

Нормальные электроны движутся как бы с трением. Поэтому они создают как реактивное, так и активное сопротивление.

А зависит ли сопротивление от температуры проводника?

Проведём опыт. Соберём электрическую цепь, состоящую из источника тока, проволочной спирали и гальванометра ( рис. 197 ). Из опыта следует, что при нагревании спирали показания гальванометра уменьшаются. Вывод очевиден: при увеличении температуры сопротивление металлов увеличивается.

Удельное сопротивление вещества металлического проводника зависит от концентрации свободных носителей заряда и частоты их столкновений с ионами кристаллической решётки, совершающими колебательные движения около положений устойчивого равновесия.

В металлических проводниках концентрация свободных электронов практически постоянна для данного проводника и не зависит от температуры. Однако частота столкновений свободных электронов с ионами кристаллической решётки с ростом температуры возрастает. Это приводит к возрастанию удельного сопротивления металлического проводника при повышении температуры.

При описании температурной зависимости удельного сопротивления проводника вводят температурный коэффициент сопротивления α, численно равный относительному изменению удельного сопротивления вещества проводника при приращении его температуры на 1 К:

где ρ ₀ и ρ — удельные сопротивления вещества проводника соответственно при температуре T₀ = 273 К (0 °С) и данной температуре Т .

Из формулы (1) следует, что

где ΔT = T - T₀ — приращение абсолютной температуры проводника, которое совпадает с приращением температуры по шкале Цельсия ΔT = Δt . Таким образом, удельное сопротивление вещества металлического проводника возрастает с увеличением температуры.

График этой зависимости представлен на рисунке 197.1.

Поскольку сопротивление проводника , то, пренебрегая незначительной температурной зависимостью отношения , можно записать:

где R₀ и R — сопротивления проводника соответственно при температуре T₀ = 273 К (0 °С) и данной температуре T(t).

Для металлических проводников эти формулы применимы при температурах T > 140 К . У всех металлов при повышении температуры сопротивление возрастает, т. е. температурный коэффициент сопротивления α — величина положительная. Для большинства металлов (но не сплавов) при температурах от 0 для 100 °С среднее значение температурного коэффициента сопротивления .

Зависимость сопротивления металлов от температуры используют в специальных приборах — термометрах сопротивления ( рис. 198 ).

Широкое распространение получили термометры сопротивления из чистых металлов, особенно платины и меди, которые конструктивно представляют собой металлическую проволоку, намотанную на жёсткий каркас (из кварца, фарфора, слюды), заключённый в защитную оболочку (из металла, кварца, фарфора, стекла) ( рис. 199 ).Платиновые термометры сопротивления применяют для измерения температуры в пределах от –263 до 1064 °С, медные — от –50 до 180 °С.

Если при изготовлении электроизмерительных приборов требуются проводники, сопротивление которых должно как можно меньше зависеть от температуры окружающей среды, то используют специальные сплавы — константан и манганин. Температурный коэффициент у константана в 820 раз, а у манганина в 510 раз меньше, чем у серебра.

Сверхпроводимость. При очень низких температурах сопротивление некоторых металлических проводников резко (скачком) уменьшается до нуля. Впервые это обнаружил в 1911 г. нидерландский физик Г. Камерлинг-Оннес ( 1853–1926 ). Он экспериментально установил, что при температуре Т ≤ 4,12 К (по современным измерениям 4,15 К) электрическое сопротивление ртути исчезает. Позже многочисленными опытами было установлено, что это явление характерно для многих проводников. Температуру, при которой электрическое сопротивление проводника уменьшается до нуля, называют критической температурой. Состояние проводника при этом называют сверхпроводимостью, а сам проводник — сверхпроводником. Каждый сверхпроводящий металл характеризуется своей критической температурой. Явление сверхпроводимости свойственно не только некоторым металлам, но и сплавам, полупроводникам и полимерам.

Если в сверхпроводнике создать электрический ток, то он будет существовать в нём неограниченно долго. При этом для поддержания тока нет необходимости в источнике тока. Это указывает на перспективу использования явления сверхпроводимости при передаче электрической энергии.

Сверхпроводящие соединения нашли применение в качестве материала обмоток электромагнитов для создания сильных магнитных полей в мощных электрических двигателях, генераторах, ускорителях и др. Разрабатывают проекты сверхпроводящих электронно-вычислительных машин. Уже созданы компактные интегральные схемы на сверхпроводниках, обладающие рядом преимуществ по сравнению с имеющимися аналогами.

1. Какова природа электрического тока в металлах?

2. Как было доказано, что носителями электрического заряда в металлах являются электроны?

3. Как изменяется сопротивление металлического проводника при повышении температуры?

4. Что понимают под электронным газом?

5. Что называют температурным коэффициентом сопротивления?

6. На каком свойстве проводников основано действие термометра сопротивления?

7. В чём проявляется явление сверхпроводимости?

Определите сопротивление алюминиевого проводника при температуре t₂ = 90 °С , если при температуре t₁ = 20 °С его сопротивление R₁ = 4,0 Ом . Температурный коэффициент сопротивления алюминия α = 4,2 · 10 -3 К -1 .

Решение: Согласно формуле сопротивления проводника при температурах t₁ и t₂ соответственно

Решая систему уравнений, получим:

Упражнение 24.1

1. В металлическом проводнике длиной l = 1,0 м проходит электрический ток. Число электронов проводимости, упорядоченно движущихся в этом проводнике, N = 2,5 · 10 19 , а сила тока I = 2,0 мА . Определите модуль средней скорости упорядоченного движения электронов проводимости.

2. Сопротивление металлического проводника при температуре t₀ = 0,0 °С в b = 1,5 раза меньше, чем при температуре t = 120 °С . Определите температурный коэффициент сопротивления вещества проводника.

3. При температуре t₀ = 0,0 °С сопротивление вольфрамового ( α = 5,0 · 10 -3 К -1 ) проводника R₀ = 40 Ом . При прохождении электрического тока по проводнику его сопротивление увеличилось на ΔR = 100 Ом . Определите изменение температуры проводника.

4. При температуре t₁ = 20,0 °С сопротивление латунного ( α = 6,50 · 10 -3 К -1 ) проводника R₁ = 30,0 Ом . Проводник подключили к сети, напряжение которой U = 120 В . Определите температуру проводника, если сила электрического тока, проходящего по нему, I = 800 мА .

5. При нагревании медного проводника, площадь поперечного сечения которого S = 0,10 мм 2 , его сопротивление увеличилось на ΔR = 30 мОм . Определите изменение внутренней энергии проводника. Для меди температурный коэффициент сопротивления α = 4,3 · 10 -3 К -1 , плотность D = 8,9 · 10 3 , удельная теплоёмкость с = 380 , удельное сопротивление ρ = 1,7 · 10 -8 Ом·м .

Читайте также: