Сила тока в металлическом проводнике при его нагревании
Электричество — неотъемлемый признак нашей эпохи. Абсолютно всё вокруг завязано на нём. Любой современный человек, даже без технического образования, знает, что электрический ток, текущий по проводам, способен в некоторых случаях нагревать их, зачастую до очень высоких температур. Казалось бы, это заведомо всем известно и не стоит упоминания. Однако, как объяснить это явление? Почему и как происходит нагрев проводника?
Опыты Ленца
Перенесемся в 19 век-эпоху накопления знаний и подготовки к технологическому прыжку 20 века. Эпоха, когда по всему миру различные учёные и просто изобретатели-самоучки чуть ли не ежедневно открывают что-то новое, зачастую тратя огромное количество времени на исследования и, при этом, не представляя конечный результат.
Один из таких людей, русский учёный Эмилий Христианович Ленц, увлекался электричеством, на тогдашнем примитивном уровне, пытаясь рассчитывать электрические цепи. В 1832 году Эмилий Ленц «застрял» с расчётами, так как параметры его смоделированной цепи «источник энергии — проводник — потребитель энергии» сильно разнились от опыта к опыту. Зимой 1832-1833 года учёный обнаружил, что причиной нестабильности является кусочек платиновой проволоки, принесённый им с холода. Отогревая или охлаждая проводник, Ленц также заметил что существует некая зависимость между силой тока, электрическим сопротивлением и температурой проводника.

При определённых параметрах электрической цепи проводник быстро оттаивал и даже слегка нагревался. Измерительных приборов в те времена практически никаких не существовало — невозможно было точно измерить ни силу тока, ни сопротивление. Но это был русский физик, и он проявил смекалку. Если это зависимость, то почему бы ей не быть обратимой?
Для того чтобы измерить количество тепла, выделяемого проводником, учёный сконструировал простейший «нагреватель» — стеклянная ёмкость, в которой находился спиртосодержащий раствор и погружённый в него платиновый проводник-спираль. Подавая различные величины электрического тока на проволоку, Ленц замерял время, за которое раствор нагревался до определённой температуры. Источники электрического тока в те времена были слишком слабы, чтобы разогреть раствор до серьёзной температуры, потому визуально определить количество испарившегося раствора не представлялось возможным. Из-за этого процесс исследования очень затянулся — тысячи вариантов подбора параметров источника питания, проводника, долгие замеры и последующий анализ.
Закон Джоуля-Ленца
В итоге, спустя десятилетие, в 1843 году Эмилий Ленц выставил на всеобщее обозрение научного сообщества результат своих опытов в виде закона. Однако, оказалось, что его опередили! Пару лет назад английский физик Джеймс Прескотт Джоуль уже проводил аналогичные опыты и также представил общественности свои результаты. Но, тщательно проверив все работы Джеймса Джоуля, русский учёный выяснил что собственные опыты гораздо точнее, наработан больший объём исследований, потому, русской науке есть чем дополнить английское открытие.
Научное сообщество рассмотрело оба результата исследований и объединила их в одно, тем самым закон Джоуля переименовали в закон Джоуля-Ленца. Закон утверждает, что количество теплоты, выделяемое проводником при протекании по нему электрического тока , равно произведению силы этого тока в квадрате, сопротивлению проводника и времени, за которое по проводнику течёт ток. Или формулой:
Q — количество выделяемого тепла (Джоули)
I — сила тока, протекающего через проводник (Амперы)
R — сопротивление проводника (Омы)
t — время прохождения тока через проводник (Секунды)
Почему греется проводник
Как же объясняется нагрев проводника? Почему он именно греется, а не остаётся нейтральным или охлаждается? Нагрев происходит из-за того, что свободные электроны, перемещающиеся в проводнике под действием электрического поля, бомбардируют атомы молекул металла, тем самым передавая им собственную энергию, которая переходит в тепловую. Если изъясняться совсем просто: преодолевая материал проводника, электрический ток как бы «трётся», соударяется электронами о молекулы проводника. Ну а , как известно, любое трение сопровождается нагревом. Следовательно, проводник будет нагреваться пока по нему бежит электрический ток.

Из формулы также следует — чем выше удельное сопротивление проводника и чем выше сила тока протекающего по нему, тем выше будет нагрев . Например, если последовательно соединить проводник-медь (удельное сопротивление 0,018 Ом·мм²/м) и проводник-алюминий (0,027 Ом·мм²/м), то при протекании через цепь электрического тока алюминий будет нагреваться сильнее чем медь из-за более высокого сопротивления. Поэтому, кстати, не рекомендуется в быту делать скрутки медных и алюминиевых проводов друг с другом — будет неравномерный нагрев в месте скрутки. В итоге — подгорание с последующим пропаданием контакта.
Применение закона Джоуля-Ленца в жизни
Открытие закона Джоуля-Ленца имело огромные последствия для практического применения электрического тока. Уже в 19 веке стало возможным создать более точные измерительные приборы, основанные на сокращении проволочной спирали при её нагреве протекающим током определённой величины — первые стрелочные вольтметры и амперметры. Появились первые прототипы электрических обогревателей, тостеров, плавильных печей – использовался проводник с высоким удельным сопротивлением, что позволяло получить довольно высокую температуру.
Были изобретены плавкие предохранители, биметаллические прерыватели цепи (аналоги современных тепловых реле защиты), основанные на разнице нагрева проводников с разным удельным сопротивлением. Ну и, конечно же, обнаружив что при определённой силе тока проводник с высоким удельным сопротивлением способен нагреться докрасна , данный эффект использовали в качестве источника света. Появились первые лампочки.
Проводник (угольная палочка, бамбуковая нить, платиновая проволока и т.д.) помещали в стеклянную колбу, откачивали воздух для замедления процесса окисления и получали незатухаемый, чистый и стабильный источник света – электрическую лампочку

Заключение
Таки образом, можно сказать что на законе Джоуля-Ленца держится чуть ли не вся электрика и электротехника. Открыв этот закон, появилась возможность уже заранее предсказать некоторые будущие проблемы в освоении электричества. Например, из-за нагрева проводника передача электрического тока на большое расстояние сопровождается потерями этого тока на тепло. Соответственно, чтобы компенсировать эти потери нужно занизить передаваемый ток, компенсируя это высоким напряжением. А уже на оконечном потребителе, понижать напряжение и получать более высокий ток.
Закон Джоуля-Ленца неотступно следует из одной эпохи технологического развития в другую. Даже сегодня мы постоянно наблюдаем его в быту – закон проявляется всюду, и не всегда люди ему рады. Сильно греющийся процессор персонального компьютера, пропадание света из-за обгоревшей скрутки «медь-алюминий»,выбитая вставка-предохранитель, выгоревшая из-за высокой нагрузки электропроводка – всё это тот самый закон Джоуля-Ленца.
Раз уж заговорили про ДжОУля )) Читайте статья про ОУ — Операционный усилитель.
Сила тока в металлическом проводнике при его нагревании
Так, энергия электрического поля переходит во внутреннюю энергию проводника. Его температура увеличивается.
При протекании электрического тока по проводнику его внутренняя энергия увеличивается.
В растворах солей, кислот, щелочей свободными заряженными частицами являются ионы. Они также будут взаимодействовать с атомами вещества.
От чего зависит количество теплоты, выделяемое проводником с током?
Электрический ток проходит по проводнику. Он нагревается. При этом он контактирует с окружающей средой, а не находится в вакууме. По этой причине проводник начинает выделять некоторое количество теплоты $Q$. То есть проводник взаимодействует с окружающей средой посредством теплопередачи.
Заглянув внутрь проводника и объяснив его нагревание, мы можем предположить, что количество теплоты зависит как минимум от двух величин: от сопротивления и от силы тока.
Давайте разберемся, почему мы выбрали именно эти величины.
- Сопротивление
Чем больше сопротивление проводника, тем больше он препятствует прохождению электрического тока. Значит, тем сильнее ионы в металле взаимодействуют со свободными электронами и тем больше энергии они получают. Значит, при прохождении тока по проводнику с большим сопротивлением должно выделяться большое количество теплоты. Мы предполагаем, что сопротивление проводника прямо пропорционально выделяемому количеству теплоты. - Сила тока
Сила тока рассчитывается по формуле: $I = \frac$. Получается, что чем больше сила тока, тем большее количество свободных частиц проходит через поперечное сечение проводника в единицу времени. Значит, происходит и больше столкновений с ионами и атомами проводника. Следовательно, тем больше количество теплоты, которое выделится при прохождении электрического тока по проводнику.
Зависимость количества теплоты, выделяющегося в проводнике, от его сопротивления
Давайте опытным путем подтвердим наше первое предположение. Соберем электрическую цепь, состоящую из двух нагревателей и источника тока. Все элементы соединим последовательно.
Нагреватели у нас имеют одинаковые размеры, но сделаны из разных материалов. Соответственно, они имеют различные сопротивления $R_1$ и $R_2$. При этом $R_1 > R_2$.
Опустим нагреватели в калориметры (приборы для измерения количества теплоты) с одинаковым количеством воды. Начальная температура воды в обоих сосудах тоже одинакова.
Замкнем цепь. Теперь через нагреватели течет электрический ток (рисунок 1). Сила тока в них одинакова, потому что они соединены последовательно.
Мы увидим, что вода нагреется быстрее в первом калориметре. Это значит, что она получила большее количество теплоты. Именно в этом калориметре у нас и находится нагреватель с большим сопротивлением $R_1$. Наше предположение подтвердилось.
Чем больше сопротивление проводника, тем большее количество теплоты выделяется при прохождении по нему электрического тока.
Зависимость количества теплоты, выделяющегося в проводнике, от силы тока в нем
Теперь проверим наше второе предположение. Соберем электрическую цепь, состоящую из лампы накаливания, реостата, амперметра и источника тока.
Передвигая ползунок реостата, будем постепенно увеличивать силу тока в цепи. Мы увидим, что будет увеличиваться и яркость лампочки (рисунок 2).
Получается, что при увеличении силы тока, у нас увеличивается количество теплоты, которые выделяет нить накаливания лампы. Предположение №2 подтверждено.
Чем больше сила тока в проводнике, тем большее количество теплоты выделяется при прохождении по нему электрического тока.
Подобные опыты в одно время, но независимо друг от друга проводили двое ученых. Один из них — это уже известный нам Джеймс Джоуль, а второй — русский физик Эмилий Христианович Ленц (рисунок 3).

Рисунок 3. Эмилий Ленц (1804—1865) — российский физик, один из основоположников электротехники
Анализируя измеренные в ходе опытов величины, ученые смогли математически сформулировать закон, описывающий количество теплоты, выделяемой проводником при прохождении по нему электрического тока.
Закон Джоуля-Ленца:
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени;
$Q = I^2Rt$.
Этот же результат мы можем получить, выполнив простые математические действия с уже известными нам величинами. Но для этого нам осталось разобрать всего один нюанс — закон сохранения энергии при нагревании проводника током.
Закон сохранения энергии при нагревании проводника током
По закону сохранения энергии мы знаем, что энергия не приходит из ниоткуда и не уходит в никуда.
Откуда у нас появилась какая-то дополнительная энергия в проводнике, которая пошла на его нагревание? Это энергия электрического поля, созданного источником тока. Если же поле имеет какую-то энергию, то оно может совершить какую-то работу, что и происходит на практике. При этом наш проводник нагревается — получает какое-то количество теплоты (энергии). Получается, что происходит превращение электрической энергии во внутреннюю энергию тела.
Если ток производит только тепловое действие, то выделенное в проводнике количество теплоты будет равно работе электрического тока, совершенной за это время:
$Q = A$.
Математический вывод закона Джоуля-Ленца
Нагревание при прохождении электрического тока происходит в неподвижных металлических проводниках. Получается, что работа тока будет идти на увеличение внутренней энергии проводника. Нагретый проводник будет эту энергию передавать окружающим телам путем теплопередачи: $Q = A$.
Работа электрического тока рассчитывается по формуле: $A = UIt$.
Тогда $Q = A = UIt$.
Подставим это выражение в формулу для количества теплоты:
$Q = UIt = IR \cdot It = I^2Rt$.
Мы пришли к верной записи закона Джоуля-Ленца.
Упражнения
Упражнение №1
Какое количество теплоты выделится за $30 \space мин$ проволочной спиралью сопротивлением $20 \space Ом$ при силе тока, равной $5 \space А$?
Дано:
$t = 30 \space мин$
$R = 20 \space Ом$
$I = 5 \space А$
СИ:
$t = 1800 \space с$
Показать решение и ответ
Решение:
Используем закон Джоуля-Ленца:
$Q = I^2Rt$.
$Q = 5^2 \space А^2 \cdot 20 \space Ом \cdot 1800 \space с = 900 \space 000 \space Дж = 900 \space кДж$.
Ответ: $Q = 900 \space кДж$.
Упражнение №2
С какой целью провода в местах соединения не просто скручивают, а еще и спаивают? Ответ обоснуйте.
Скручивая один проводник с другим, мы получаем утолщенное и уплотненное место их соединения. Сопротивление на таком участке будет больше, чем у самих проводов. А чем больше сопротивление проводника, тем больше тепла будет выделяться при прохождении по нему электрического тока. Такой участок будет сильно нагреваться.
Спайка же позволяет сделать место соединения проводов более однородным. Это практически не изменяет сопротивления. Таким образом, мы избегаем нагревания проводов в месте их соединения друг с другом.
Упражнение №3
Спираль нагревательного прибора — рефлектора — при помощи шнура и вилки соединяется с розеткой. Шнур состоит из проводов, подводящих ток к спирали, покрытых изоляцией. Спираль и провода соединены последовательно. Как распределяется подаваемое от сети напряжение между проводами и спиралью? Почему спираль раскаляется, а провода почти не нагреваются? Какими особенностями устройства спирали и проводов достигается эта разница?
Будем опираться на закон Джоуля-Ленца: $Q = I^2Rt$.
Спираль раскаляется, а провода — нет. Это означает, что на спирали выделяется намного больше количества теплоты $Q$, чем в проводах. Если сила тока одинакова, значит причина этому — сопротивление $R$.
Поэтому мы делаем вывод, что спираль раскаляется, так как обладает намного большим сопротивлением, чем провода. Такое устройство обуславливается материалами, из которых сделаны спираль и провода. Удельное сопротивление спирали точно больше удельного сопротивления проводов ($R = \frac)$. Также провода тоньше спирали. Их площадь поперечного сечения намного меньше площади поперечного сечения спирали нагревательного прибора. Поэтому в проводах выделяется меньшее количество теплоты, чем в спирали.
Что будет с напряжением в такой цепи? Запишем закон Джоуля-Ленца в таком виде: $Q = UIt$. Сказано, что все элементы в этой цепи соединены последовательно. Значит сила тока $I$ во всех ее участках будет одинакова.
Получается, что напряжение на спирали будет больше, чем напряжение на концах проводов.
Упражнение №4
В цепь источника тока включены последовательно три проволоки одинакового сечения и одинаковой длины: медная, стальная и никелиновая. Какая из них больше нагреется? Ответ обоснуйте и по возможности проверьте на опыте.
Начнем с теории. По закону Джоуля-Ленца: чем больше сопротивление проводника, тем большее количество теплоты выделится в нем. Сила тока на всех участках цепи будет одинакова из-за типа соединения.
Сопротивление проводников рассчитывается по формуле: $R = \frac$. Так как размеры проволок одинаковы, то определять все будет величина удельного сопротивления каждого материала.
Из таблицы возьмем значения удельных сопротивлений:
$\rho_ = 1.1 \frac$,
$\rho_ = 0.4 \frac$,
$\rho_м = 0.017 \frac$.
Самым большим сопротивлением будет обладать нихромовая проволока. Она нагреется больше остальных.
Теперь проведем опыт.
Соберем электрическую цепь из трех проволок и источника тока. Все элементы соединим последовательно.
Через какое-то время вы сможете увидеть подтверждение нашим теоретическим выводам. Нихромовая проволока нагреется до белого каления, никелиновая — начнет краснеть (рисунок 4). Медная проволока визуально останется такой же.
Обратите внимание, что визуально оценить эффект нагревания в таком случае проще, чем пробовать при малых температурах определить на ощупь, какая проволока нагрелась больше или пытаться использовать термометр.
Нагревание проводников электрическим током

Одним из свойств электрического тока является нагрев проводников, по которым он протекает. Этот эффект был замечен многими исследователями, но его понимание пришло только выяснения механизма взаимодействия заряженных частиц с атомами и молекулами проводников. Нагрев приводит к выделению тепла и повышению температуры, а количество выделяемого тепла можно рассчитать с помощью формулы закона Джоуля-Ленца.
Почему нагреваются проводники
Электрический ток — это упорядоченное движение заряженных частиц. В проводниках этими частицами выступают отрицательно заряженные электроны. Воздействие электрического поля сообщает электронам дополнительную кинетическую энергию. В процессе движения они сталкиваются с атомами (или молекулами) проводника, отдавая часть приобретенной энергии. По этой причине начинает увеличиваться внутренняя энергия вещества, что приводит к повышению температуры и выделению тепла.
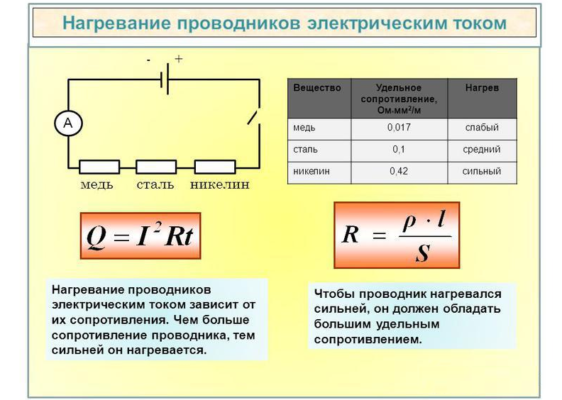
Рис. 1. Электрический ток в проводнике нагревает проводник
Если взять обычную лампочку накаливания и подключить ее к источнику напряжения через реостат (переменное сопротивление), то можно наблюдать тепловой эффект от протекания тока. Постепенно увеличивая ток, мы можем сначала на ощупь почувствовать, что стеклянная колба лампочки постепенно начнет нагреваться, а затем увидим, как начинает светиться раскаленная нить накаливания.
Заметим, что в этом эксперименте подводящие провода сильно не нагреваются и не светятся. Это происходит потому, что сопротивление нити накаливания намного больше сопротивления подводящих проводов .
На основании этого и других экспериментов можно сделать следующие предположения:
- чем больше сопротивление, тем сильнее нагреваются проводники. То есть количество теплоты Q, которое выделяется при протекании электрического тока по проводнику, прямо пропорционально величине сопротивления проводника R;
- чем больше сила тока, тем большее количества тепла выделяется. При возрастании тока большее количество частиц проходит через поперечное сечение проводника в единицу времени, то есть число столкновений возрастает, а значит больше энергии передается атомам проводника.
Формулу для вычисления количества тепла получили независимо друг от друга в 1842 г. английский физик Джеймс Джоуль и российский ученый Эмилий Ленц:
Q — количество теплоты, Дж;
Согласно закону Ома:
где U — напряжение, В.
Пользуясь этой формулой, закон Джоуля-Ленца может быть представлен еще в одном варианте, когда известно напряжение на участке проводника, а сила тока неизвестна:
Формулы закона Джоуля-Ленца справедливы тогда, когда работа, совершаемая электрическим током идет исключительно на нагревание. Если в цепи есть потребление энергии на выполнение механической работы (электродвигатель) или на совершение химических реакций (электролит), то для расчета необходимо применять другие формулы.
Плюсы и минусы от нагрева электрическим током
- Плюсы. Нагревание проводников электрическим током находит свое применение в различных полезных приборах и устройствах: электроплитах, чайниках, кофеварках, кипятильниках, фенах, утюгах, обогревателях.
- Минусы. Очень часто инженерам-электронщикам приходится бороться с этим эффектом для того, чтобы, например, обеспечить работоспособность электронных плат, которые напичканы огромным количеством электронных деталей, микросхем и т.д. Все эти элементы греются в соответствие с законом Джоуля-Ленца. И если не предпринять меры для принудительного охлаждения с помощью металлических радиаторов или вентиляторов (кулеров), то платы быстро выйдут из строя от перегрева.
Часто для быстрого соединения проводов многие пользуются способом “скрутки”. Это приводит к значительному увеличению сопротивления, а следовательно, место “скрутки” будет греться сильнее, чем остальная часть проводки. Поэтому скрутка проводов часто бывает причиной пожаров в домах и квартирах. Для улучшения контакта требуется хорошо пропаять это место.
Что мы узнали?
Итак, мы поговорили кратко о нагревании проводников электрическим током. Нагрев проводников происходит из-за того, что электроны, движущиеся упорядоченно с определенной скоростью, сталкиваются с атомами вещества и отдают часть своей энергии, которая переходит в тепло. Количество тепла можно определить, применив формулу Джоуля-Ленца.
В случае, когда проводник неподвижен и химических превращений в нем не происходит, то работа тока целиком расходуется на нагревание проводника. Количество теплоты, выделяющееся в проводнике за конечный промежуток времени при прохождении постоянного тока I, рассчитывается по формуле
Формула (2.7) выражает закон Джоуля-Ленца для участка цепи постоянного тока: количество теплоты, выделяемое постоянным электрическим током на участке цепи, равно произведению квадрата силы тока на время его прохождения и электрическое сопротивление этого участка цепи.
Так как IR = U, то формулу (2.7) можно переписать в виде
Если сила тока изменяется со временем, то количество теплоты, выделяющееся за время t, вычисляется по формуле
Закон Джоуля-Ленца в дифференциальной форме (для данной точки проводника с током) имеет вид
где ω − плотность тепловой мощности; σ − удельная электропроводность; Е− напряженность электрического поля в данной точке проводника; Е * − напряженность поля сторонних сил.
Примеры решения задач
Задача 1. За время τ = 20 с при равномерно возраставшей силе тока от нуля до Io в проводнике сопротивлением R = 5 Ом выделилось количество теплоты Q = 4 кДж. Найти Io.
| Io – ? | Решение: Так как ток равномерно возрастает, то зависимость силы тока от времени имеет вид . (1) |
| τ = 20 с R = 5 Ом Q = 4 кДж |
По закону Джоуля-Ленца за время dt в проводнике выделится количество тепла
Полное количество тепла за время от 0 до τ
Ответ: I0 = 11 А.
Задача 2. При включении электромотора в сеть с напряжением U = 220 В он потребляет ток I = 5 А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление обмотки мотора R = 6 Ом.
| Pп – ? η – ? | Решение: Полная мощность, потребляемая мотором: , Р0 = 1100 Вт. |
| U = 220 В I = 5 А R = 6 Ом |
Мощность, выделяющаяся в виде тепла:
Полезная мощность (механическая)
Ответ: η = 86,4%.
Задача 3. Источник тока с ЭДС замкнут на реостат. При силе тока I1 = 0,2 А и I2 = 2,4 А на реостате выделяется одинаковая мощность. Найти:
1) при какой силе тока на реостате выделяется максимальная мощность?
2) чему равна сила тока короткого замыкания?
| I – ? Iкз – ? | Решение: При силе тока I1 на реостате выделяется мощность , при силе тока I2 , |
| I1 = 0,2 А | |
| I2 = 2,4 А P1 = P2 |
где R1 и R2 – сопротивления реостата в каждом случае. По условию P1 = P2, поэтому
По закону Ома для полной цепи
Из (2) и (3) выражаем R1 и R2:
подставив их в (1), получаем:
Отсюда находим отношение :
Максимальная мощность выделяется при условии R = r, при этом ток
Ток короткого замыкания
Ответ:I = 1,3 А; Iкз = 2,6 А.
Задача 4. При изменении внешнего сопротивления с R1 = 6 Ом до R2 = 21 Ом. КПД схемы увеличился вдвое. Чему равно внутреннее сопротивление источника тока r ?
| r − ? | Решение: При сопротивлении R1 КПД источника тока , а при сопротивлении R2 |
| R1 = 6 Ом R2 = 21 Ом η2 = 2η1 |
Так как по условию задачи η2=2η1, то
Отсюда выражаем r:
Ответ: r = 14 Ом.
Задача 5. Две батареи с ЭДС ε1 = 20 В и ε2 = 30 В и внутренними сопротивлениями r1 = 4 Ом и r2 = 60 Ом соединены параллельно и подключены к нагрузке R = 100 Ом. Найти: 1) мощность, которая выделяется в нагрузке; 2) параметры ε и r генератора, которым можно заменить батареи без изменения тока в нагрузке; 3) КПД этого генератора.
| P – ? ε, r – ? η – ? | Решение: 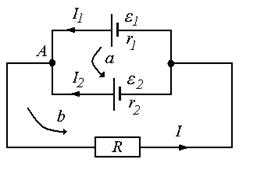 Рис. 52 |
| ε1 = 20 В ε2 = 30 В r1 = 4 Ом r2 = 60 Ом R = 100 Ом |
Используя правила Кирхгофа, найдем токи I1, I2, I в узле A:
Для контура a с обходом против часовой стрелки
Для контура b с обходом против часовой стрелки
Решим систему линейных уравнений (1) – (3) относительно I1, I2, I.
Из (1) выразим I
Умножая уравнение (2) на R, а уравнение (5) – на r1, и складывая их, получаем:
Подставляя (6) в выражение (2), находим I1:
Подставляя выражения (6) и (7) в (4), находим I:
В нагрузке выделяется мощность:
Находим параметры генератора. Если данные в задаче батареи заменить на одну с ЭДС ε и внутренним сопротивлением r, то через сопротивление R потек бы ток
Преобразуем выражение (8), поделив числитель и знаменатель дроби на (r1+r2), получим
Для того чтобы эти выражения были одинаковыми, необходимо выполнение условий:
Тепловое действие тока, плотность тока и их влияние на нагрев проводников
Под тепловым действием электрического тока понимают выделение тепловой энергии в процессе прохождения тока по проводнику. Когда через проводник проходит ток, образующие ток свободные электроны сталкиваются с ионами и атомами проводника, нагревая его.
Выделяемое при этом количество теплоты можно определить с помощью закона Джоуля-Ленца, который формулируется так: количество теплоты, выделяемое при прохождении электрического тока через проводник, равно произведению квадрата тока, сопротивления данного проводника и времени прохождения тока через проводник.
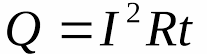
Приняв ток в амперах, сопротивление в омах, а время в секундах, получим количество теплоты в джоулях. А учитывая что произведение тока на сопротивление — есть напряжение, а произведение напряжения на ток — мощность, в результате оказывается, что количество выделенной теплоты в данном случае равно количеству электрической энергии, переданной данному проводнику во время прохождения по нему тока. То есть электрическая энергия преобразуется в тепловую.
Получение тепловой энергии из электрической широко применяется с давних времен в различной технике. Электронагревательные приборы, такие как обогреватели, водонагреватели, электрические плиты, паяльники, электропечи и т. д., а также электросварка, лампы накаливания и многое другое используют именно этот принцип для получения тепла.

Но в большом количестве электрических устройств нагрев, вызываемый током, вреден: электродвигатели, трансформаторы, провода, электромагниты и т. д. - в данных устройствах, не предназначенных для получения тепла, нагрев снижает их КПД, мешает эффективной работе, и даже может привести к аварийным ситуациям.
Для любого проводника, в зависимости от параметров окружающей среды, характерно определенное допустимое значение величины тока, при котором проводник заметно не нагревается.
Так, например, для нахождения допустимой токовой нагрузки на провода, используют параметр «плотность тока», характеризующий ток, приходящийся на 1 кв.мм площади поперечного сечения данного проводника.
Допустимая плотность тока для каждого проводящего материала в определенных условиях своя, она зависит от многих факторов: от вида изоляции, интенсивности охлаждения, температуры окружающей среды, площади поперечного сечения и т. д.
К примеру для электрических машин, где обмотки изготавливают, как правило, из меди, величина предельно допустимой плотности тока не должна превышать 3-6 ампер на кв.мм. Для лампы накаливания, а точнее для ее вольфрамовой нити, - не более 15 ампер на кв.мм.
Для проводов осветительных и силовых сетей предельно допустимая плотность тока принимается исходя из вида их изоляции и площади поперечного сечения.
Если материалом проводника служит медь, а изоляция резиновая, то при площади сечения, например, в 4 кв.мм допускается плотность тока не более 10,2 ампер на кв.мм, а если сечение 50 кв.мм, то допустимая плотность тока будет всего 4,3 ампера на кв.мм. Если же проводники указанной площади не имеют изоляции, то допустимые плотности тока будут соответственно 12,5 и 5,6 ампер на кв.мм.

С чем же связано понижение допустимой плотности тока для проводников большего сечения? Дело в том, что проводники с существенной площадью поперечного сечения, в отличие от проводников малого сечения, имеют больший объем проводящего материала расположенного внутри, и получается что внутренние слои проводника сами окружены нагревающимися слоями, которые мешают отводу тепла изнутри.
Чем больше площадь поверхности проводника по отношению к его объему, - тем большую плотность тока способен выдержать проводник не перегреваясь. Неизолированные проводники допускают нагрев до более высокой температуры, так как от них тепло отводится прямо в окружающую среду, изоляция этому не препятствует, и охлаждение происходит быстрее, поэтому для них допускается более высокая плотность тока чем для проводников в изоляции.
Если превысить допустимый для проводника ток, он начнет перегреваться, и в какой-то момент его температура окажется чрезмерной. Изоляция обмотки электродвигателя, генератора или просто проводки, может в таких условиях обуглиться или загореться, что приведет к короткому замыканию и пожару. Если же говорить о неизолированном проводе, то он при высокой температуре может просто расплавиться и разорвать цепь, в которой служит проводником.

Превышение допустимого тока принято предотвращать. Поэтому в электрических установках обычно принимают специальные меры с целью автоматического отключения от источника питания той части цепи или того электроприемника, в котором случилась перегрузка по току или короткое замыкание. Для этого служат автоматические выключатели, плавкие предохранители и другие устройства, несущие аналогичную функцию — разорвать цепь при перегрузке.
Из закона Джоуля-Ленца следует, что перегрев проводника может произойти не только из-за превышения тока через его поперечное сечение, но и из-за более высокого сопротивления проводника. По этой причине для полноценной и надежной работы любой электрической установки крайне важно сопротивление, особенно в местах соединения друг с другом отдельных проводников.

Если проводники соединены не плотно, если их контакт друг с другом не качественный, то сопротивление в месте соединения (так называемое переходное сопротивление в месте контакта) окажется выше чем для цельного участка проводника той же длины.
В результате прохождения тока через такое некачественное, не достаточно плотное соединение, место данного соединения будет перегреваться, что чревато возгоранием, выгоранием проводников или даже пожаром.
Чтобы этого избежать, концы соединяемых проводников надежно зачищают, облуживают и оснащают кабельными наконечниками (впаивают или прессуют) или гильзами, которые обеспечивают запас на переходное сопротивление в месте контакта. Такие наконечники можно плотно закрепить на клеммах электрической машины при помощи болтов.
К электрическим аппаратам, предназначенным для включения и выключения тока, также применяют меры по уменьшению переходного сопротивления между контактами.
Читайте также:
