Сила тока в металлическом проводнике при его нагревании увеличивается или уменьшается
Свободные электроны – это электроны, не связанные с определенными атомами.
Сверхпроводимость – физическое явление, заключающееся в скачкообразном падении до нуля сопротивления вещества.
Температурный коэффициент сопротивления - величина, равная относительному изменению электрического сопротивления участка электрической цепи или удельного сопротивления вещества при изменении температуры на 1 К.
Основная и дополнительная литература по теме урока:
Мякишев Г. Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 216-224.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. - М.: Дрофа, 2009.- С.81-89.
М.М. Балашов О природе М., Просвещение, 1991г.
Е.А. Марон, А.Е. Марон Сборник качественных задач по физике. М., Просвещение, 2006
Я.И. Перельман Занимательная физика. М.: “Наука”, 1991.
Основное содержание урока
Все тела по проводимости электрического тока делятся на проводники, полупроводники и диэлектрики. Для того чтобы электрическую энергию доставить от источника тока потребителю составляют электрические цепи. В большинстве случаев в электрической цепи используются металлические провода. По физической природе зарядов – носителей электрического тока, электропроводность подразделяют на:
Какие заряженные частицы движутся в металлах при наличии тока?
После открытия в 1897 году английским ученым Дж. Дж. Томсоном электрона стали разрабатываться теории, объясняющие электропроводность металлов. Автором первой теории был Пауль Друде – немецкий физик. Эта теория нуждалась в опытном обосновании. В 1901 г. немецкий физик Э. Рикке поставил опыт по исследованию прохождения тока в металлах.
Результаты опыта свидетельствовали о том, что в переносе заряда в металлах ионы не участвуют. Впоследствии вопросом проводимости металлов заинтересовались и другие учёные. В 1913 году российские учёные Л. И. Мандельштам и Н. Д. Папалекси провели опыты по исследованию проводимости металлов. Суть опытов сводилась к тому, что катушка, на которую наматывали металлическую проволоку приводили во вращательное движение и резко тормозили. При торможении электроны продолжали двигаться по инерции и гальванометр, соединенный с катушкой фиксировал появление тока. По направлению отклонения стрелки гальванометра было установлено, что ток создается движением отрицательно заряженных частиц. На основании измерения отношения заряда частиц к их массе выяснилось, что ток создается движением свободных электронов. Аналогичный опыт был поставлен в 1916 году американскими учеными Т. Стюартом и Р. Толменом. Результаты опытов говорили, что ток в металлах создается движением электронов.

После анализа имеющихся данных о прохождении тока в металлах разными учеными была разработана современная классическая теория проводимости тока металлами. Основные положения электронной теории проводимости металлов.
1. Металл можно описать следующей моделью: кристаллическая решетка ионов погружена в идеальный электронный газ, состоящий из свободных электронов. У большинства металлов каждый атом ионизирован, поэтому концентрация свободных электронов приблизительно равна концентрации атомов 1023- 1029м-3 и почти не зависит от температуры.
2.Свободные электроны в металлах находятся в непрерывном хаотическом движении.
3. Электрический ток в металле образуется только за счет упорядоченного движения свободных электронов.
Опираясь на данную теорию удалось объяснить основные законы электрического тока в металлах. Исходя из электронной теории можно найти связь между силой тока в металлах и скоростью движения электронов.
Сила тока равна произведению заряда электрона, их концентрации, площади сечения проводника и средней скорости движения электронов:
ОтсюдаЕсли в эту формулу подставлять числовые данные силы тока, концентрации и площади сечения для разных металлов, то мы увидим, что средняя скорость движения электронов составляет всего лишь какие-то доли миллиметра в секунду. Когда говорят о скорости распространения тока имеют в виду скорость распространения электрического поля в проводнике, которое равно скорости света.
На силу тока в проводнике влияет и сопротивление проводника. Опыт показывает, что сопротивление металлов зависит от температуры. Увеличение сопротивления можно объяснить тем, при повышении температуры увеличивается скорость и амплитуда хаотического движения ионов кристаллической решетки металла и свободных электронов. Это приводит к более частым их соударениям, что затрудняет направленное движение электронов, то есть увеличивает электрическое сопротивление.
зависимость сопротивления металлов от температуры выражается формулой:
При нагревании размеры проводника практически не меняются, в основном меняется удельное сопротивление. Учет зависимости сопротивления от температуры используется в термометрах сопротивления.
Формула зависимости удельного сопротивления металлического проводника от температуры имеет вид:
где ρ0 - удельное сопротивление при 0 градусов,
α - температурный коэффициент сопротивления.
Графиком зависимости ⍴(t) является прямая.

Хотя коэффициент α довольно мал, учет зависимости сопротивления от температуры при расчете нагревательных приборов совершенно необходим.
При понижении температуры сопротивление металлов должно уменьшаться. В 1911 году датский физик Х. Каммерлинг - Оннес открыл явление, названное сверхпроводимостью. Исследуя зависимость сопротивления ртути от температуры, он обнаружил, что при температуре 4,12 К сопротивление ртути исчезает. В сверхпроводящее состояние могут перейти многие химические соединения и сплавы. Некоторые вещества, переходящие при низких температурах в сверхпроводящее состояние, не являются проводниками при обычных температурах.
Вещества, находящиеся в сверхпроводящем состоянии, приобретают новые свойства. Наиболее важным из них является способность длительное время (многие годы) поддерживать без затухания электрический ток в проводниках.
Классическая электронная теория не способна объяснить явление сверхпроводимости. Теоретическое объяснение явления сверхпроводимости на основе квантово-механических представлений было дано учеными Дж. Бардиным, Дж. Шриффером (США) и Н. Н. Боголюбовым (СССР) в 1957 г.
В 1986 году была обнаружена высокотемпературная сверхпроводимость (при 100 К).
В настоящее время ведутся интенсивные работы по поиску новых веществ переходящими в сверхпроводящее состояние при более высокой температуре. Ученые надеются получить вещество в сверхпроводящем состоянии при комнатной температуре. Если удастся создать сверхпроводник при нормальной температуре, то будет решена проблема передачи электроэнергии по проводам без потерь.
Следует отметить, что до настоящего времени механизм высокотемпературной сверхпроводимости керамических материалов до конца не выяснен.
Открытие вещества, переходящего в сверхпроводящее состояние при комнатной температуре, позволило бы упростить решение многих технических вопросов. Во-первых, отсутствие сопротивления означает отсутствие каких-либо потерь на нагревание. Отсутствие нагревания и потерь энергии на него чрезвычайно важно для электродвигателей и электронной вычислительной техники, а также для передачи электроэнергии.
В сверхпроводниках из-за отсутствия сопротивления протекают чрезвычайно высокие токи, создающие сильные магнитные поля, что может применяться при термоядерном синтезе для удержания высокотемпературной плазмы в реакторе.
На сегодняшний момент в некоторых странах существует железнодорожная сеть с поездами на магнитной подушке. После открытия сверхпроводимости Камерлинг-Оннес, пытаясь создать сверхпроводящий электромагнит, обнаружил, что изменение тока, или же магнитные поля, разрушают эффект сверхпроводимости. Только к середине двадцатого века удалось создать сверхпроводящие электромагниты. На данный момент продолжаются исследования по изучению высокотемпературной сверхпроводимости.
Разбор типовых тренировочных заданий
1. Сопротивление железного проводника при 0 0 С и 600 0 С равны соответственно 2 Ом и 10 Ом. Каков температурный коэффициент железа?
Зависимость сопротивления металлов от температуры определяется формулой
Из этой формулы выразим температурный коэффициент железа – α
После подстановки числовых данных получаем
2. Какова скорость дрейфа электронов в медном проводе диаметром 5 мм, по которому к стартеру грузовика подводится ток 100 А. Молярная масса медиСила тока в проводнике равна:
Выразим скорость из этой формулы:
Концентрацию электронов найдем по формуле:
Число электронов найдём по формуле:
Площадь сечения равна:
Учитывая всё это запишем конечную формулу для расчёта скорости дрейфа электронов:
Электрический ток в металлах
В этом листке мы приступаем к подробному изучению того, как осуществляется прохождение электрического тока в различных проводящих средах — твёрдых телах, жидкостях и газах.
Напомним, что необходимым условием возникновения тока является наличие в среде достаточно большого количества свободных зарядов, которые могут начать упорядоченное движение под действием электрического поля. Такие среды как раз и называются проводниками электрического тока.
Наиболее широко распространены металлические проводники. Поэтому начинаем мы с вопросов распространения электрического тока в металлах.
Мы много раз говорили о свободных электронах, которые являются носителями свободных зарядов в металлах. Вам хорошо известно, что электрический ток в металлическом проводнике образуется в результате направленного движения свободных электронов.
Свободные электроны
Металлы в твёрдом состоянии имеют кристаллическую структуру: расположение атомов в пространстве характеризуется периодической повторяемостью и образует геометрически правильный рисунок, называемый кристаллической решёткой.
Атомы металлов имеют небольшое число валентных электронов, расположенных на внешней электронной оболочке. Эти валентные электроны слабо связаны с ядром, и атом легко может их потерять.
Когда атомы металла занимают места в кристаллической решётке, валентные электроны покидают свои оболочки — они становятся свободными и отправляются «гулять» по всему кристаллу (а именно, свободные электроны перемещаются по внешним орбиталям соседних атомов. Эти орбитали перекрываются друг с другом вследствие близкого расположения атомов в кристаллической решётке, так что свободные электроны оказываются «общей собственностью» всего кристалла). В узлах кристаллической решётки металла остаются положительные ионы, пространство между которыми заполнено «газом» свободных электронов (рис. 1 ).
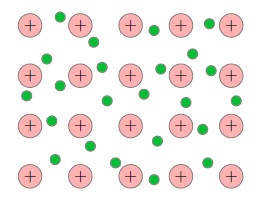
Рис. 1. Свободные электроны
Свободные электроны и впрямь ведут себя подобно частицам газа (другой адекватный образ — электронное море, которое «омывает» кристаллическую решётку) — совершая тепловое движение, они хаотически снуют туда-сюда между ионами кристаллической решётки. Суммарный заряд свободных электронов равен по модулю и противоположен по знаку общему заряду положительных ионов, поэтому металлический проводник в целом оказывается электрически нейтральным.
Газ свободных электронов является «клеем», на котором держится вся кристаллическая структура проводника. Ведь положительные ионы отталкиваются друг от друга, так что кристаллическая решётка, распираемая изнутри мощными кулоновскими силами, могла бы разлететься в разные стороны. Однако в тоже самое время ионы металла притягиваются к обволакивающему их электронному газу и, как ни в чём не бывало, остаются на своих местах, совершая лишь тепловые колебания в узлах кристаллической решётки вблизи положений равновесия.
Что произойдёт, если металлический проводник включить в замкнутую цепь, содержащую источник тока? Свободные электроны продолжают совершать хаотическое тепловое движение, но теперь — под действием возникшего внешнего электрического поля — они вдобавок начнут перемещаться упорядоченно. Это направленное течение электронного газа, накладывающееся на тепловое движение электронов, и есть электрический ток в металле (поэтому свободные электроны называются также электронами проводимости). Скорость упорядоченного движения электронов в металлическом проводнике, как нам уже известно, составляет приблизительно 0,1мм/с.
Опыт Рикке
Почему мы решили, что ток в металлах создаётся движением именно свободных электронов? Положительные ионы кристаллической решётки также испытывают на себе действие внешнего электрического поля. Может, они тоже перемещаются внутри металлического проводника и участвуют в создании тока?
Упорядоченное движение ионов означало бы постепенный перенос вещества вдоль направления электрического тока. Поэтому надо просто пропускать ток по проводнику на протяжении весьма длительного времени и посмотреть, что в итоге получится. Такого рода эксперимент и был поставлен Э.Рикке в 1901 году.
В электрическую цепь были включены три прижатых друг к другу цилиндра: два медных по краям и один алюминиевый между ними (рис. 2 ). По этой цепи пропускался электрический ток в течение года.
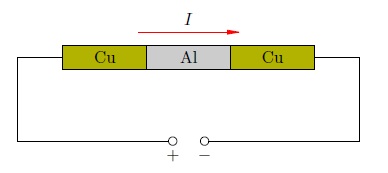
Рис. 2. Опыт Рикке
За год сквозь цилиндры прошёл заряд более трёх миллионов кулон. Предположим, что каждый атом металла теряет по одному валентному электрону, так что заряд иона равен элементарному заряду Кл. Если ток создаётся движением положительных ионов, то нетрудно подсчитать (сделайте это сами!), что такая величина прошедшего по цепи заряда соответствует переносу вдоль цепи около 2кг меди.
Однако после разъединения цилиндров было обнаружено лишь незначительное проникновение металлов друг в друга, обусловленное естественной диффузией их атомов (и не более того). Электрический ток в металлах не сопровождается переносом вещества, поэтому положительные ионы металла не принимают участия в создании тока.
Опыт Стюарта–Толмена
Прямое экспериментальное доказательство того, что электрический ток в металлах создаётся движением свободных электронов, было дано в опыте Т.Стюарта и Р.Толмена (1916 год).
Эксперименту Стюарта–Толмена предшествовали качественные наблюдения, сделанные четырьмя годами ранее русскими физиками Л.И.Мандельштамом и Н.Д.Папалекси. Они обратили внимание на так называемый электроинерционный эффект: если резко затормозить движущийся проводник, то в нём возникает кратковременный импульс тока. Эффект объясняется тем, что в течение небольшого времени после торможения проводника его свободные заряды продолжают двигаться по инерции.
Однако никаких количественных результатов Мандельштам и Папалекси не получили, и наблюдения их опубликованы не были. Честь назвать опыт своим именем принадлежит Стюарту и Толмену, которые не только наблюдали указанный электроинерционный эффект, но и произвели необходимые измерения и расчёты.
Установка Стюарта и Толмена показана на рис. 3 .
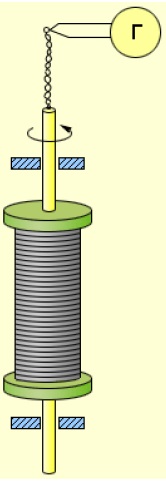
Рис. 3. Опыт Стюарта–Толмена
Катушка большим числом витков металлического провода приводилась в быстрое вращение вокруг своей оси. Концы обмотки с помощью скользящих контактов были подсоединены к специальному прибору — баллистическому гальванометру, который позволяет измерять проходящий через него заряд.
После резкого торможения катушки в цепи возникал импульс тока. Направление тока указывало на то, что он вызван движением отрицательных зарядов. Измеряя баллистическим гальванометром суммарный заряд, проходящий по цепи, Стюарт и Толмен вычислили отношение заряда одной частицы к её массе. Оно оказалось равно отношению для электрона, которое в то время уже было хорошо известно.
Так было окончательно выяснено, что носителями свободных зарядов в металлах являются свободные электроны. Как видите, этот давно и хорошо знакомый вам факт был установлен сравнительно поздно — учитывая, что металлические проводники к тому моменту уже более столетия активно использовались в самых разнообразных экcпериментах по электромагнетизму (сравните, например, с датой открытия закона Ома — 1826 год. Дело, однако, заключается в том, что сам электрон был открыт лишь в 1897 году).
Зависимость сопротивления от температуры
Опыт показывает, что при нагревании металлического проводника его сопротивление увеличивается. Как это объяснить?
Причина проста: с повышением температуры тепловые колебания ионов кристаллической решётки становятся более интенсивными, так что число соударений свободных электронов с ионами возрастает. Чем активнее тепловое движение решётки, тем труднее электронам пробираться сквозь промежутки между ионами (Представьте себе вращающуюся проходную дверь. В каком случае труднее проскочить через неё: когда она вращается медленно или быстро? :-)). Скорость упорядоченного движения электронов уменьшается, поэтому уменьшается и сила тока (при неизменном напряжении). Это и означает увеличение сопротивления.
Как опять-таки показывает опыт, зависимость сопротивления металлического проводника от температуры с хорошей точностью является линейной:
Здесь — сопротивление проводника при . График зависимости (1) является прямой линией (рис. 4 ).
Множитель называется температурным коэффициентом сопротивления. Его значения для различных металлов и сплавов можно найти в таблицах.
Длина проводника и его площадь поперечного сечения при изменении температуры меняются несущественно. Выразим и через удельное сопротивление:
и подставим эти формулы в (1) . Получим аналогичную зависимость удельного сопротивления от температуры:
Коэффициент весьма мал (для меди, например, ), так что температурной зависимостью сопротивления металла часто можно пренебречь. Однако в ряде случаев считаться с ней приходиться. Например, вольфрамовая спираль электрической лампочки раскаляется до такой степени, что её вольт-амперная характеристика оказывается существенно нелинейной.
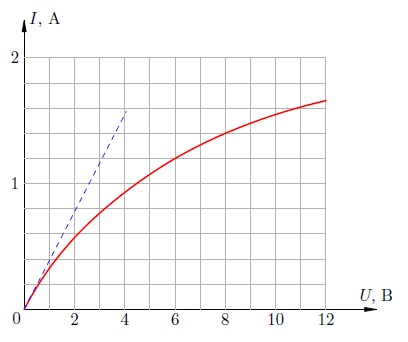
Рис. 5. Вольт-амперная характеристика лампочки
Так, на рис. 5 приведена вольт-амперная характеристика автомобильной лампочки. Если бы лампочка представляла собой идеальный резистор, её вольт-амперная характеристика была прямой линией в соответствии с законом Ома. Эта прямая изображена синим пунктиром.
Однако по мере роста напряжения, приложенного к лампочке, график отклоняется от этой прямой всё сильнее и сильнее. Почему? Дело в том, что с увеличением напряжения ток через лампочку возрастает и больше разогревает спираль; сопротивление спирали поэтому также увеличивается. Следовательно, сила тока хотя и продолжит возрастать, но будет иметь всё меньшее и меньшее значение по сравнению с тем, которое предписывается «пунктирной» линейной зависимостью тока от напряжения.
Нагревание проводников электрическим током

Одним из свойств электрического тока является нагрев проводников, по которым он протекает. Этот эффект был замечен многими исследователями, но его понимание пришло только выяснения механизма взаимодействия заряженных частиц с атомами и молекулами проводников. Нагрев приводит к выделению тепла и повышению температуры, а количество выделяемого тепла можно рассчитать с помощью формулы закона Джоуля-Ленца.
Почему нагреваются проводники
Электрический ток — это упорядоченное движение заряженных частиц. В проводниках этими частицами выступают отрицательно заряженные электроны. Воздействие электрического поля сообщает электронам дополнительную кинетическую энергию. В процессе движения они сталкиваются с атомами (или молекулами) проводника, отдавая часть приобретенной энергии. По этой причине начинает увеличиваться внутренняя энергия вещества, что приводит к повышению температуры и выделению тепла.
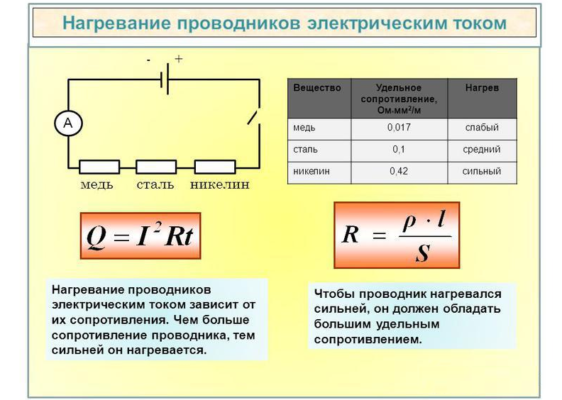
Рис. 1. Электрический ток в проводнике нагревает проводник
Если взять обычную лампочку накаливания и подключить ее к источнику напряжения через реостат (переменное сопротивление), то можно наблюдать тепловой эффект от протекания тока. Постепенно увеличивая ток, мы можем сначала на ощупь почувствовать, что стеклянная колба лампочки постепенно начнет нагреваться, а затем увидим, как начинает светиться раскаленная нить накаливания.
Заметим, что в этом эксперименте подводящие провода сильно не нагреваются и не светятся. Это происходит потому, что сопротивление нити накаливания намного больше сопротивления подводящих проводов .
Закон Джоуля-Ленца
На основании этого и других экспериментов можно сделать следующие предположения:
- чем больше сопротивление, тем сильнее нагреваются проводники. То есть количество теплоты Q, которое выделяется при протекании электрического тока по проводнику, прямо пропорционально величине сопротивления проводника R;
- чем больше сила тока, тем большее количества тепла выделяется. При возрастании тока большее количество частиц проходит через поперечное сечение проводника в единицу времени, то есть число столкновений возрастает, а значит больше энергии передается атомам проводника.
Формулу для вычисления количества тепла получили независимо друг от друга в 1842 г. английский физик Джеймс Джоуль и российский ученый Эмилий Ленц:
Q — количество теплоты, Дж;
Согласно закону Ома:
где U — напряжение, В.
Пользуясь этой формулой, закон Джоуля-Ленца может быть представлен еще в одном варианте, когда известно напряжение на участке проводника, а сила тока неизвестна:
Формулы закона Джоуля-Ленца справедливы тогда, когда работа, совершаемая электрическим током идет исключительно на нагревание. Если в цепи есть потребление энергии на выполнение механической работы (электродвигатель) или на совершение химических реакций (электролит), то для расчета необходимо применять другие формулы.
Плюсы и минусы от нагрева электрическим током
- Плюсы. Нагревание проводников электрическим током находит свое применение в различных полезных приборах и устройствах: электроплитах, чайниках, кофеварках, кипятильниках, фенах, утюгах, обогревателях.
- Минусы. Очень часто инженерам-электронщикам приходится бороться с этим эффектом для того, чтобы, например, обеспечить работоспособность электронных плат, которые напичканы огромным количеством электронных деталей, микросхем и т.д. Все эти элементы греются в соответствие с законом Джоуля-Ленца. И если не предпринять меры для принудительного охлаждения с помощью металлических радиаторов или вентиляторов (кулеров), то платы быстро выйдут из строя от перегрева.
Часто для быстрого соединения проводов многие пользуются способом “скрутки”. Это приводит к значительному увеличению сопротивления, а следовательно, место “скрутки” будет греться сильнее, чем остальная часть проводки. Поэтому скрутка проводов часто бывает причиной пожаров в домах и квартирах. Для улучшения контакта требуется хорошо пропаять это место.
Что мы узнали?
Итак, мы поговорили кратко о нагревании проводников электрическим током. Нагрев проводников происходит из-за того, что электроны, движущиеся упорядоченно с определенной скоростью, сталкиваются с атомами вещества и отдают часть своей энергии, которая переходит в тепло. Количество тепла можно определить, применив формулу Джоуля-Ленца.
Как зависит сопротивление от температуры
В своей практической деятельности каждый электрик встречается с разными условиями прохождения носителей зарядов в металлах, полупроводниках, газах и жидкостях. На величину тока влияет электрическое сопротивление, которое различным образом изменяется под влиянием окружающей среды.
Одним из таких факторов является температурное воздействие. Поскольку оно значительно изменяет условия протекания тока, то учитывается конструкторами в производстве электрооборудования. Электротехнический персонал, участвующий в обслуживании и эксплуатации электроустановок, обязан грамотно использовать эти особенности в практической работе.
Влияние температуры на электрическое сопротивление металлов
В школьном курсе физики предлагается провести такой опыт: взять амперметр, батарейку, отрезок проволоки, соединительные провода и горелку. Вместо амперметра с батарейкой можно подключить омметр или использовать его режим в мультиметре.
Далее необходимо собрать электрическую схему, показанную на картинке и замерить величину тока в цепи. Его значение показано на шкале миллиамперметра стрелкой черного цвета.
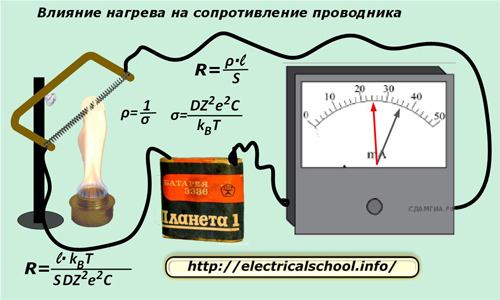
Теперь поднесем пламя горелки к проволоке и станем ее нагревать. Если смотреть на амперметр, то будет видно, что стрелка станет перемещаться влево и достигнет положения, отмеченного красным цветом.
Результат опыта демонстрирует, что при нагревании металлов их проводимость уменьшается, а сопротивление возрастает.
Математическое обоснование этого явления приведено формулами прямо на картинке. В нижнем выражении хорошо видно, что электрическое сопротивление «R» металлического проводника прямо пропорционально его температуре «Т» и зависит еще от нескольких параметров.
Как нагрев металлов ограничивает электрический ток на практике
Ежедневно при включении освещения мы встречаемся с проявлением этого свойства у ламп накаливания. Проведем несложные измерения на лампочке с мощностью 60 ватт.
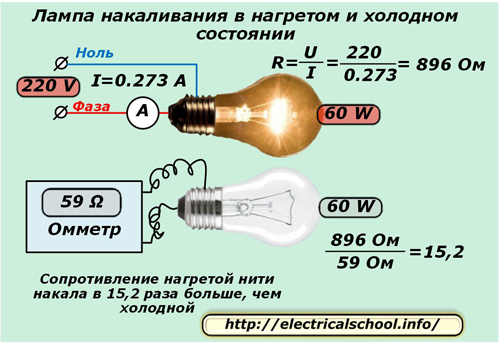
Самым простым омметром, питающемся от низковольтной батарейки 4,5 V, замерим сопротивление между контактами цоколя и увидим значение 59 Ом. Этой величиной обладает нить накала в холодном состоянии.
Вкрутим лампочку в патрон и через амперметр подключим к ней напряжение домашней сети 220 вольт. Стрелка амперметра покажет 0,273 ампера. По закону Ома для участка цепи определим сопротивление нити в нагретом состоянии. Оно составит 896 Ом и превысит предыдущее показание омметра в 15,2 раза.
Такое превышение предохраняет металл тела накала от перегорания и разрушения, обеспечивая его длительную работоспособность под напряжением.
Переходные процессы при включении
При работе нити накала на ней создается тепловой баланс между нагревом от проходящего электрического тока и отводом части тепла в окружающую среду. Но, на первоначальном этапе включения при подаче напряжения возникают переходные процессы, создающие бросок тока, который может привести к перегоранию нити.
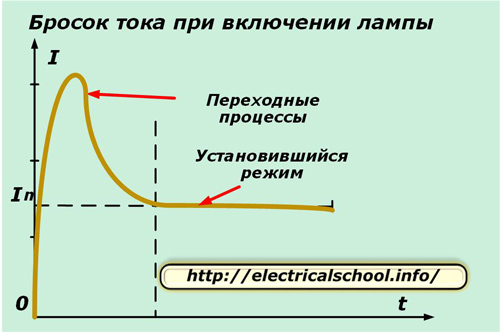
Переходные процессы протекают за короткое время и вызваны тем, что скорость возрастания электрического сопротивления от нагрева металла не успевает за увеличением тока. После их окончания устанавливается рабочий режим.
Во время длительного свечения лампы постепенно толщина ее нити доходит до критического состояния, которое приводит к перегоранию. Чаще всего этот момент возникает при очередном новом включении.
Для продления ресурса лампы различными способами уменьшают этот бросок тока, используя:
1. устройства, обеспечивающие плавную подачу и снятие напряжения;
2. схемы последовательного подключения к нити накала резисторов, полупроводников или терморезисторов (термисторов).
Пример одного из способов ограничения пускового тока для автомобильных светильников показан на картинке ниже.
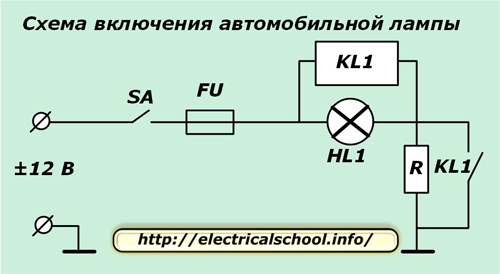
Здесь ток на лампочку подается после включения тумблера SA через предохранитель FU и ограничивается резистором R, у которого номинал подбирается так, чтобы бросок тока во время переходных процессов не превышал номинальное значение.
При нагреве нити накала ее сопротивление возрастает, что ведет к увеличению разности потенциалов на ее контактах и параллельно подключенной обмотке реле KL1. Когда напряжение достигнет величины уставки реле, то нормально открытый контакт KL1 замкнется и зашунтирует резистор. Через лампочку начнет протекать рабочий ток уже установившегося режима.
Влияние температуры металла на его электрическое сопротивление используется в работе измерительных приборов. Их называют термометрами сопротивления.
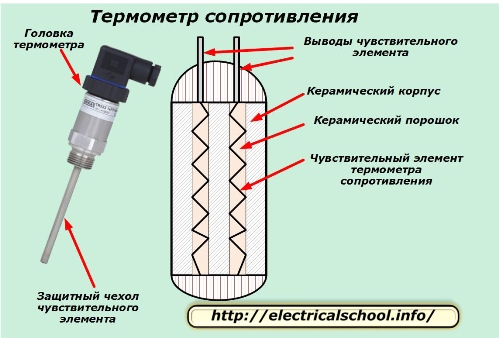
Их чувствительный элемент выполняют тонкой проволочкой из металла, сопротивление которой тщательно замерено при определенных температурах. Эту нить монтируют в корпусе со стабильными термическими свойствами и закрывают защитным чехлом. Созданная конструкция помещается в среду, температуру которой необходимо постоянно контролировать.
На выводы чувствительного элемента монтируются провода электрической схемы, которыми подключается цепь замера сопротивления. Его величина пересчитывается в значения температуры на основе ранее произведенной калибровки прибора.
Бареттер — стабилизатор тока
Так называют прибор, состоящий из стеклянного герметичного баллона с газообразным водородом и металлической проволочной спиралью из железа, вольфрама или платины. Эта конструкция по внешнему виду напоминает лампочку накаливания, но она обладает специфической вольт-амперной нелинейной характеристикой.
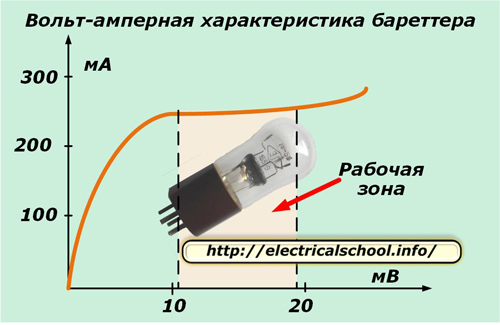
На ВАХ в определенном ее диапазоне образуется рабочая зона, которая не зависит от колебаний приложенного на тело накала напряжения. На этом участке бареттер хорошо компенсирует пульсации питания и работает в качестве стабилизатора тока на подключенной последовательно к нему нагрузке.
Работа бареттера основана на свойстве тепловой инерции тела накала, которая обеспечивается маленьким сечением нити и высокой теплопроводностью окружающего ее водорода. За счет этого при снижении напряжения на приборе ускоряется отвод тепла с его нити.
Это основное отличие бареттера от осветительных ламп накаливания, в которых для поддержания яркости свечения стремятся уменьшить конвективные потери тепла с нити.
В обычных условиях среды при охлаждении металлического проводника происходит уменьшение его электрического сопротивления.
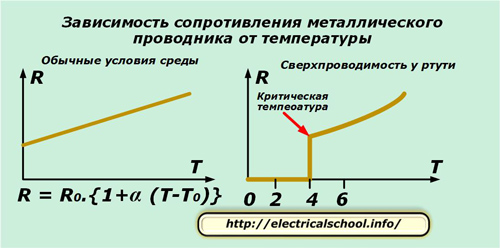
При достижении критической температуры, близкой к нулю градусов по системе измерения Кельвина, происходит резкое падение сопротивления до нулевого значения. На правой картинке показана такая зависимость для ртути.
Это явление, названное сверхпроводимостью, считается перспективной областью для исследований с целью создания материалов, способных значительно снизить потери электроэнергии при ее передаче на огромные расстояния.
Однако, продолжающиеся изучения сверхпроводимости выявили ряд закономерностей, когда на электрическое сопротивление металла, находящегося в области критических температур, влияют другие факторы. В частности, при прохождении переменного тока с повышением частоты его колебаний возникает сопротивление, величина которого доходит до диапазона обычных значений у гармоник с периодом световых волн.
Влияние температуры на электрическое сопротивление/проводимость газов
Газы и обычный воздух являются диэлектриками и не проводят электрический ток. Для его образования нужны носители зарядов, которыми выступают ионы, образующиеся в результате воздействия внешних факторов.
Нагрев способен вызвать ионизацию и движение ионов от одного полюса среды к другому. Убедиться в этом можно на примере простого опыта. Возьмем то же оборудование, которым пользовались для определения влияния нагрева на сопротивление металлического проводника, только вместо проволоки к проводам подключим две металлические пластины, разделенные воздушным пространством.

Подсоединенный к схеме амперметр покажет отсутствие тока. Если между пластинами поместить пламя горелки, то стрелка прибора отклонится от нулевого значения и покажет величину проходящего через газовую среду тока.
Таким образом установили, что в газах при нагревании происходит ионизация, приводящая к движению электрически заряженных частиц и снижению сопротивления среды.
На значении тока сказывается мощность внешнего приложенного источника напряжения и разность потенциалов между его контактами. Она способна при больших значениях пробить изоляционный слой газов. Характерным проявлением подобного случая в природе является естественный разряд молнии во время грозы.
Примерный вид вольт-амперной характеристики протекания тока в газах показан на графике.
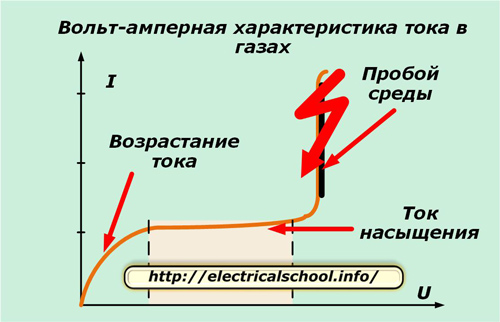
На начальном этапе под действие температуры и разности потенциалов наблюдается рост ионизации и прохождение тока примерно по линейному закону. Затем кривая приобретает горизонтальное направление, когда увеличение напряжения не вызывает рост тока.
Третий этап пробоя наступает тогда, когда высокая энергия приложенного поля так разгоняет ионы, что они начинают соударяться с нейтральными молекулами, массово образуя из них новые носители зарядов. В результате ток резко возрастает, образуя пробой диэлектрического слоя.
Практическое использование проводимости газов
Явление протекания тока через газы используется в радиоэлектронных лампах и люминесцентных светильниках.
Для этого внутри герметичного стеклянного баллона с инертным газом располагают два электрода:
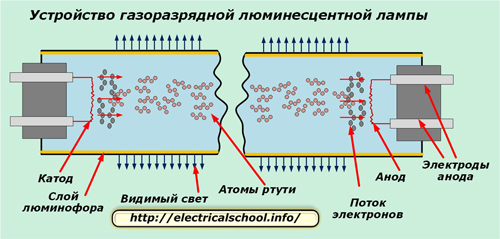
У люминесцентной лампы они выполнены в виде нитей накала, которые разогреваются при включении для создания термоэлектронной эмиссии. Внутренняя поверхность колбы покрыта слоем люминофора. Он излучает видимый нами спектр света, образующийся при инфракрасном облучении, исходящем от паров ртути, бомбардируемых потоком электронов.
Ток газового разряда возникает при приложении напряжения определенной величины между электродами, расположенными по разным концам колбы.
Когда одна из нитей накала перегорит, то на этом электроде нарушится электронная эмиссия и лампа гореть не будет. Однако, если увеличить разность потенциалов между катодом и анодом, то снова возникнет газовый разряд внутри колбы и свечение люминофора возобновится.
Это позволяет использовать светодиодные колбы с нарушенными нитями накала и продлять их ресурс работы. Только следует учитывать, что при этом в несколько раз надо поднять на ней напряжение, А это значительно повышает потребляемую мощность и риски безопасного использования.
Влияние температуры на электрическое сопротивление жидкостей
Прохождение тока в жидкостях создается в основном за счет движения катионов и анионов под действием приложенного извне электрического поля. Лишь незначительную часть проводимости обеспечивают электроны.
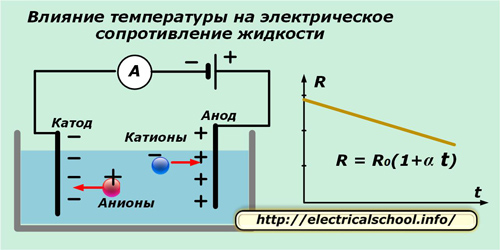
Влияние температуры на величину электрического сопротивления жидкого электролита описывается формулой, приведенной на картинке. Поскольку в ней значение температурного коэффициента α всегда отрицательно, то с увеличением нагрева проводимость возрастает, а сопротивление падает так, как показано на графике.
Это явление необходимо учитывать при зарядке жидкостных автомобильных (и не только) аккумуляторных батарей.
Влияние температуры на электрическое сопротивление полупроводников
Изменение свойств полупроводниковых материалов под воздействием температуры позволило использовать их в качестве:
Таким названием обозначают полупроводниковые приборы, изменяющие свое электрическое сопротивление под влиянием тепла. Их температурный коэффициент сопротивления (ТКС) значительно выше, чем у металлов.
Величина ТКС у полупроводников может иметь положительное или отрицательное значение. По этому параметру их разделяют на позитивные «РТС» и негативные «NTC» термисторы. Они обладают различными характеристиками.
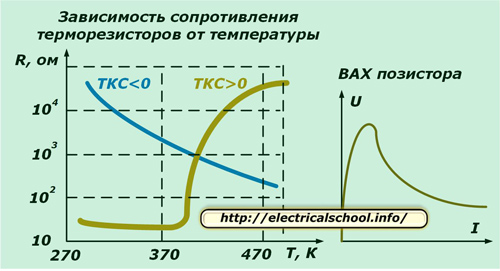
Для работы терморезистора выбирают одну из точек на его вольт-амперной характеристике:
линейный участок применяют для контроля температуры либо компенсации изменяющихся токов или напряжений;
нисходящая ветвь ВАХ у элементов с ТКС
Применение релейного терморезистора удобно при контроле или измерениях процессов электромагнитных излучений, происходящих на сверхвысоких частотах. Это обеспечило их использование в системах:
1. контроля тепла;
2. пожарной сигнализации;
3. регулирования расхода сыпучих сред и жидкостей.
Кремниевые терморезисторы с маленьким ТКС>0 используют в системах охлаждения и стабилизации температуры транзисторов.
Эти полупроводники работают на основе явления Зеебека: при нагреве спаянного места двух разрозненных металлов на стыке замкнутой цепи возникает ЭДС. Таким способом они превращают тепловую энергию в электричество.
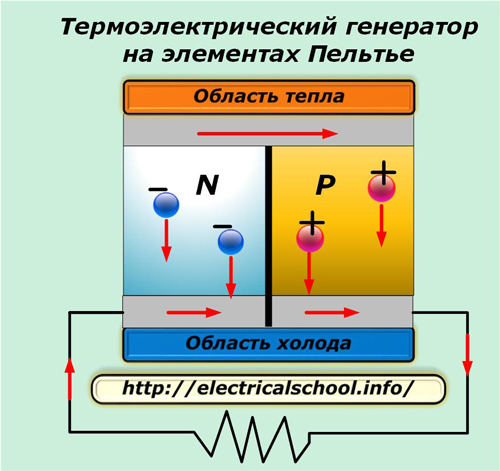
Конструкцию из двух таких элементов называют термопарой. Ее КПД лежит в пределах 7÷10%.
Термоэлементы используют в измерителях температур цифровых вычислительных устройств, требующих миниатюрные габариты и высокую точность показаний, а также в качестве маломощных источников тока.
Полупроводниковые нагреватели и холодильники
Они работают за счет обратного использования термоэлементов, через которые пропускают электрический ток. При этом на одном месте спая происходит его нагрев, а на противоположном — охлаждение.
Полупроводниковые спаи на основе селена, висмута, сурьмы, теллура позволяют обеспечить разность температур в термоэлементе до 60 градусов. Это позволило создать конструкцию холодильного шкафа из полупроводников с температурой в камере охлаждения до -16 градусов.
Телеграмм канал для тех, кто каждый день хочет узнавать новое и интересное: Школа для электрика
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Как влияет нагрев на величину сопротивления
Некоторые сплавы, обладающие большим удельным сопротивлением, чем составляющие их металлы, почти не меняют удельного сопротивления с нагревом (константан, манганин и др.). Это объясняется неправильной структурой сплавов и малым средним временем свободного пробега электронов.
Величина, показывающая относительное увеличение сопротивления при нагреве материала на 1° (или уменьшение при охлаждении на 1°), называется температурным коэффициентом сопротивления .
Если температурный коэффициент обозначить через α , удельное сопротивление при to =20 о через ρ o , то при нагреве материала до температуры t1 его удельное сопротивление p1 = ρ o + αρ o (t1 - to) = ρ o(1 + ( α (t1 - to))
и соответственно R1 = Ro (1 + ( α (t1 - to))
Температурный коэффициент а для меди, алюминия, вольфрама равен 0,004 1/град. Поэтому при нагреве на 100° их сопротивление возрастает на 40%. Для железа α = 0,006 1/град, для латуни α = 0,002 1/град, для фехрали α = 0,0001 1/град, для нихрома α = 0,0002 1/град, для константана α = 0,00001 1/град, для манганина α = 0,00004 1/град. Уголь и электролиты имеют отрицательный температурный коэффициент сопротивления. Температурный коэффициент для большинства электролитов равен примерно 0,02 1/град.
Свойство проводников изменять свое сопротивления в зависимости от температуры используется в термометрах сопротивления . Измеряя сопротивление, определяют расчетным путем окружающую температуру.Константан, манганин и другие сплавы, имеющие очень небольшой температурный коэффициент сопротивления применяют для изготовления шунтов и добавочных сопротивлений к измерительным приборам.

Пример 1. Как изменится сопротивление Ro железной проволоки при нагреве ее на 520°? Температурный коэффициент а железа 0,006 1/град. По формуле R1 = Ro + Ro α (t1 - to) = Ro + Ro 0,006 ( 520 - 20 ) = 4 Ro , то есть сопротивление железной проволоки при нагреве ее на 520° возрастет в 4 раза.
Пример 2. Алюминиевые провода при температуре -20° имеют сопротивление 5 ом. Необходимо определить их сопротивление при температуре 30°.
R2 = R1 - α R1 (t2 - t1) = 5 + 0 , 004 х 5 (30 - (-20)) = 6 ом.
Свойство материалов изменять свое электрическое сопротивление при нагреве или охлаждении используется для измерения температур. Так, термосопротивления , представляющие собой проволоку из платины или чистого никеля, вплавленные в кварц, применяются для измерения температур от -200 до +600°. Полупроводниковые термосопротивления с большим отрицательным коэффициентом применяются для точного определения температур в более узких диапазонах.

Полупроводниковые термосопротивления, применяемые для измерения температур называют термисторами .
Термисторы имеют высокий отрицательный температурный коэффициент сопротивления, то есть при нагреве их сопротивление уменьшается. Термисторы выполняют из оксидных (подвергнутых окислению) полупроводниковых материалов, состоящих из смеси двух или трех окислов металлов. Наибольшее распространение имеют медно-марганцевые и кобальто-марганцевые термисторы. Последние более чувствительны к температуре.
Читайте также:
