Распространение магнитного поля в металле
В настоящее время установлено, что реальная структура электромагнитного (ЭМ) поля представляет собой необычное с общепринятых позиций вихревое векторное поле, состоящее из двух функционально связанных между собой электродинамических полей: вихревог ЭМ поля с компонентами электрической и магнитной напряженностей и поля ЭМ векторного потенциала с электрической и магнитной компонентами.
Доклад на тему «Экспериментальное наблюдение волн магнитного поля и исследование их распространения в металлах» обновлено: 14 февраля, 2020 автором: Научные Статьи.Ру
Научные Статьи.Ру / Примеры / Доклады / Неопределено / Доклад на тему «Экспериментальное наблюдение волн магнитного поля и исследование их распространения в металлах»
В настоящее время установлено, что реальная структура электромагнитного (ЭМ) поля представляет собой необычное с общепринятых позиций вихревое векторное поле, состоящее из двух функционально связанных между собой электродинамических полей: вихревог ЭМ поля с компонентами электрической и магнитной напряженностей и поля ЭМ векторного потенциала с электрической и магнитной компонентами. Указанное поле описывается системой базовых исходных фундаментальных соотношений в виде дифференциальных уравнений которые непосредственно получаются из традиционных уравнений Максвелла для ЭМ поля. Здесь — постоянная времени релаксации заряда в среде за счет электропроводности. Проведенный анализ показал, что с концептуальной точки зрения электродинамическое поле, описываемое системой физически логично называть реальное электромагнитное поле.
Основным фундаментальным своством соотношений является возможность вывода на их основе не только системы уравнений Максвелла с и компонентами, но и структурно аналогичных максвелловской трех других систем электродинамических уравнений: поля ЭМ векторного потенциала с и компонентами, электрического поля с и компонентами и, наконец, магнитное поле с и компонентами.
Поскольку при изучении взаимодействия электродинамического поля с материальной средой, в сущности, все сводится к стремлению описать энергетику явлений электромагнетизма, то однозначным подтверждением реальности структуры магнитного поля в виде двух компонент и служит следующее из уравнений соотношение энергетического баланса для потока энергии, обуславливающей явление намагничивания материальной среды.
Важно отметить, что явления динамической магнитной поляризации уже имеет прямое экспериментальное воплощение: это эффект динамического намагничивания в ферритах и магнитоупорядоченных металлах.
Форма представленных систем уравнений системы говорит о существовании волновых решений для компонент и магнитного поля. В этом можно убедиться, взяв, как обычно, ротор от одного из роторных уравнений системы, и после чего подставить в него другое роторное уравнение. В качестве иллюстрации получим волновое уравнение, например, относительно :
Здесь, согласно (2d), , — оператор Лапласа, а — фазовая скорость волны в отсутствие поглощения. Как показал анализ, компоненты и волн магнитного поля в диэлектрической среде ведут себя специфично: , то есть имеют взаимный сдвиг по фазе на π/2. Кроме того, в зависимости от частоты их амплитуды связаны между собой весьма необычно: . Конечно, математически данный результат тривиально очевиден, поскольку, согласно, компоненты магнитного поля связаны посредством производной по времени. Однако концептуально с физической точки зрения это неожиданно и требует всестороннего анализа.
Справедливости ради следует сказать, что впервые о возможности реального существования чисто магнитной поперечной волны с двумя компонентами и , сдвинутыми при распространении по фазе на π/2, официально в виде приоритета на открытие заявил Докторович еще в 1980 году, и этот факт он с удивительным упорством, достойным лучшего применения, безуспешно пытается донести до других, ссылаясь на заявленный приоритет и свою статью по этой теме, везде публикуемую многие годы. Печально, но только Время — высший судья, и именно оно расставит всех и все по своим местам! Однако будем надеяться, что независимое подтверждение этого научного достижения Докторовича будет для него серьезной поддержкой в общении с оппонентами.
Анализ уравнений системы показывает, что для проводящей среды в асимптотике металлов, как и должно быть, их волновые решения имеют вид экспоненциально затухающих в пространстве плоских волн со сдвигом фазы между компонентами на π/4.
Нужна помощь в написании доклада?
Мы - биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Наряду с теоретическим анализом, были проведены эксперименты по изучению необходимых условий возбуждения и возможность распространения электродинамических полей в металлах, отвечающие на два физически важных вопроса: волны каких полей можно реально возбудить в металлах и каковы частотные ограничения дисперсионного соотношения для проводящей среды в асимптотике металлов при длинах волн l ® ¥?
Возбуждение электродинамических полей в металле (пластинки меди и алюминия) производилось на низких частотах n = 50 — 50.103 Гц и было возможным только с помощью магнитной антенны, так как импеданс ближней зоны излучения лишь у магнитного диполя сопоставим с импедансом металлической среды. Прием прошедшего через металл излучения был возможным также лишь магнитной антенной, что однозначно говорит о наличии в принимаемом сигнале составляющей только магнитного поля и об отсутствии на выходе других составляющих электродинамического поля, названного в реальное электромагнитное поля .
Для определения закона частотной дисперсии волнового числа магнитной волны в металле его действительная часть измерялась по сдвигу фазы колебаний волны при ее прохождении в плоском слое толщиной l : , а мнимая часть — по затуханию амплитуды волны. Так как в теории металлов хорошим приближением является равенство [2], то следует ожидать, что указанные измерения посредством этих двух способов должны давать одинаковые результаты.
На рис. графически представлены результаты измерений по фазе (мелкие штрихи) и по затуханию (штрихи крупнее) для медной пластинки толщиной l = 1,9 мм. Видно, что измеренные указанными способами частотные зависимости значений и практически совпадают (различия менее 5 %) и соответствуют формуле волнового числа для плоской ЭМ волны в проводящей среде в асимптотике металлов при (сплошная линия). Все это позволяет утверждать, что известная технология индукционного нагрева металлов с помощью магнитного индуктора – это использование в реальной практике физического процесса возбуждения в проводящей среде магнитных поперечных волн. Здесь вполне уместно и пошутить: если Вам повезло и Вы сделали открытие, то загляните в книгу, там об этом уже все написано!
Резюме: установлено реальное существование в Природе волн магнитного поля, способных эффективно взаимодействовать и распространяться в металлах.
Экспериментальное наблюдение волн магнитного поля и исследование их распространения в металлах
Структура электромагнитного поля. Уравнения Максвелла. Условия реализации обычной магнитной поляризации среды. Возбуждение электродинамических полей в металле. Закон частотной дисперсии волнового числа магнитной волны. Характер частотных зависимостей.
| Рубрика | Физика и энергетика |
| Вид | доклад |
| Язык | русский |
| Дата добавления | 27.09.2008 |
| Размер файла | 93,2 K |
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
ЭКСПЕРИМЕНТАЛЬНОЕ НАБЛЮДЕНИЕ ВОЛН МАГНИТНОГО ПОЛЯ И ИССЛЕДОВАНИЕ ИХ РАСПРОСТРАНЕНИЯ В МЕТАЛЛАХ
В.В. Сидоренков
МГТУ им. Н.Э. Баумана
В настоящее время установлено [1], что реальная структура электромагнитного (ЭМ) поля представляет собой необычное с общепринятых позиций вихревое векторное поле, состоящее из двух функционально связанных между собой электродинамических полей: вихревог ЭМ поля с компонентами электрической и магнитной напряженностей и поля ЭМ векторного потенциала с электрической и магнитной компонентами. Указанное поле описывается системой базовых исходных фундаментальных соотношений в виде дифференциальных уравнений:
которые непосредственно получаются из традиционных [2] уравнений Максвелла для ЭМ поля. Здесь - постоянная времени релаксации заряда в среде за счет электропроводности. Проведенный анализ показал [1], что с концептуальной точки зрения электродинамическое поле, описываемое системой (1) физически логично называть реальное электромагнитное поле.
Основным фундаментальным своством соотношений (1) является возможность вывода на их основе не только системы уравнений Максвелла с и компонентами, но и структурно аналогичных максвелловской трех других систем электродинамических уравнений: поля ЭМ векторного потенциала с и компонентами, электрического поля с и компонентами и, наконец, магнитное поле с и компонентами. В частности, система электродинамических уравнений для магнитного поля будет иметь следующий вид:
Поскольку при изучении взаимодействия электродинамического поля с материальной средой, в сущности, все сводится к стремлению описать энергетику явлений электромагнетизма, то однозначным подтверждением реальности структуры магнитного поля в виде двух компонент и служит следующее из уравнений (2) соотношение энергетического баланса для потока энергии, обуславливающей явление намагничивания материальной среды:
Данное соотношение баланса описывает энергетику условий реализации обычной магнитной поляризации среды (первое слагаемое правой части (3)) посредством переноса извне в данную точку потока вектора соответствующей энергии. Однако это соотношение устанавливает также и наличие динамической поляризации вещества (в частности, проводящих сред) за счет действия переменной во времени магнитной компоненты поля векторного потенциала . Важно отметить, что явления динамической магнитной поляризации уже имеет прямое экспериментальное воплощение: это эффект динамического намагничивания в ферритах и магнитоупорядоченных металлах [3].
Форма представленных систем уравнений системы (2) говорит о существовании волновых решений для компонент и магнитного поля. В этом можно убедиться, взяв, как обычно, ротор от одного из роторных уравнений системы, и после чего подставить в него другое роторное уравнение. В качестве иллюстрации получим волновое уравнение, например, относительно :
Здесь, согласно (2d), , - оператор Лапласа, а - фазовая скорость волны в отсутствие поглощения. Как показал анализ [1], компоненты и волн магнитного поля в диэлектрической среде ведут себя специфично: , то есть имеют взаимный сдвиг по фазе на р/2. Кроме того, в зависимости от частоты их амплитуды связаны между собой весьма необычно: . Конечно, математически данный результат тривиально очевиден, поскольку, согласно (1), компоненты магнитного поля связаны посредством производной по времени. Однако концептуально с физической точки зрения это неожиданно и требует всестороннего анализа.
Справедливости ради следует сказать, что впервые о возможности реального существования чисто магнитной поперечной волны с двумя компонентами и , сдвинутыми при распространении по фазе на р/2, официально в виде приоритета на открытие заявил Докторович еще в 1980 году, и этот факт он с удивительным упорством, достойным лучшего применения, безуспешно пытается донести до других, ссылаясь на заявленный приоритет и свою статью по этой теме, везде публикуемую многие годы (например, [4]). Печально, но только Время - высший судья, и именно оно расставит всех и все по своим местам! Однако будем надеяться, что независимое подтверждение этого научного достижения Докторовича будет для него серьезной поддержкой в общении с оппонентами.
Анализ уравнений системы (2) показывает [1], что для проводящей среды в асимптотике металлов (), как и должно быть [2], их волновые решения имеют вид экспоненциально затухающих в пространстве плоских волн со сдвигом фазы между компонентами на р/4.
Наряду с теоретическим анализом, были проведены эксперименты по изучению необходимых условий возбуждения и возможность распространения электродинамических полей в металлах, отвечающие на два физически важных вопроса: волны каких полей можно реально возбудить в металлах и каковы частотные ограничения дисперсионного соотношения для проводящей среды в асимптотике металлов при длинах волн ?
Возбуждение электродинамических полей в металле (пластинки меди и алюминия) производилось на низких частотах = 50 50.103 Гц и было возможным только с помощью магнитной антенны, так как импеданс ближней зоны излучения лишь у магнитного диполя сопоставим с импедансом металлической среды. Прием прошедшего через металл излучения был возможным также лишь магнитной антенной, что однозначно говорит о наличии в принимаемом сигнале составляющей только магнитного поля и об отсутствии на выходе других составляющих электродинамического поля, названного в [1] реальное электромагнитное поля .
Для определения закона частотной дисперсии волнового числа магнитной волны в металле его действительная часть измерялась по сдвигу фазы колебаний волны при ее прохождении в плоском слое толщиной l : , а мнимая часть - по затуханию амплитуды волны. Так как в теории металлов хорошим приближением является равенство [2], то следует ожидать, что указанные измерения посредством этих двух способов должны давать одинаковые результаты.
На рис. графически представлены результаты измерений по фазе (мелкие штрихи) и по затуханию (штрихи крупнее) для медной пластинки толщиной l = 1,9 мм. Видно, что измеренные указанными способами частотные зависимости значений и практически совпадают (различия менее 5 %) и соответствуют формуле волнового числа для плоской ЭМ волны в проводящей среде в асимптотике металлов [2] при (сплошная линия). Все это позволяет утверждать, что известная технология индукционного нагрева металлов с помощью магнитного индуктора - это использование в реальной практике физического процесса возбуждения в проводящей среде магнитных поперечных волн. Здесь вполне уместно и пошутить: если Вам повезло и Вы сделали открытие, то загляните в книгу, там об этом уже все написано!
Однако с понижением частоты значения мнимой части волнового числа сильно отклоняются от его действительной части : в медной пластинке на частотах 2.103 Гц и алюминия ( l = 1,4 мм) при 3.103 Гц. В области этих частот при их уменьшении, график переходит от обычного к линейной зависимости по и окончательно . Соответственно, определяемая из частотная зависимость скорости распространения волны в металле сначала ведет себя обычно , но при понижении частоты переходит к const и затем окончательно . Абсолютный минимум значений скорости для пластинки меди был ~ 14 м/с, а алюминия ~ 22 м/с. Отклонение характера частотных зависимостей и от обычных определяется толщиной проводящего слоя: в толстых пластинках это изменение наступает на меньших частотах, а в тонких - на более высоких частотах. Поскольку на фиксированной частоте величина является константой данного материала и не может зависеть от толщины слоя, то наблюдаемое отклонение закона дисперсии от , справедливого для поперечных плоских волн, физически обусловлено регистрацией структуры поля ближней зоны возбуждаемого излучателем (согласно измерениям, дипольного). Именно это и отражается в измерениях с понижением частоты при приеме сигнала прошедшего через пластинку излучения.
Магнитное поле
Магнитное поле играет очень большую роль в электротехнике и электронике. Без магнитного поля не функционировали бы герконы, электромагнитные реле, соленоиды, катушки индуктивности, дроссели, трансформаторы, двигатели, динамики, генераторы электрической энергии да и вообще много чего.
Природа магнетизма
Согласно одной из легенд, когда-то давным-давно жил в Греции пастух по имени Магнес. И вот шел он как-то со своим стадом овец, присел на камень и обнаружил, что конец его посоха, сделанный из железа, стал притягиваться к этому камню. С тех пор стали называть этот камень магнетит в честь Магнеса. Этот камень представляет из себя оксид железа.

Если такой камень положить на деревянную доску на воду или подвесить на нитке, то он всегда выстраивался в определенном положении. Один его конец всегда показывал на СЕВЕР, а другой — на ЮГ.

Этим свойством камня пользовались древние цивилизации. Поэтому, это был своего рода первый компас. Потом уже стали обтачивать такой камень и делать из разные фигурки. Например, так выглядел китайский древний компас, ложка которого была сделана из того самого магнетита. Ручка у этой ложки всегда показывала на ЮГ.

Ну а далее дело шло за практичностью и маленькими габаритами. Из магнетита вытачивали маленькие стрелки, которые подвешивали на тонкую иглу посередине. Так стали появляться первые малогабаритные компасы.

Древние цивилизации, конечно, не знали еще что такое север и юг. Поэтому, одну сторону магнетита они назвали северным полюсом (North), а противоположный конец — южным (South). Названия на английском очень легко запомнить, если кто смотрел американский мультфильм «Южный парк», он же Сауз (South) парк).

Магнитные линии и магнитный поток
Вокруг магнита экспериментальным путем были обнаружены магнитные силовые линии. Эти магнитные линии создают так называемое магнитное поле.
Как вы могли заметить на рисунке, концентрация магнитных силовых линий на самых краях магнита намного больше, чем в его середине. Это говорит о том, что магнитное поле является более сильным именно на краях магнита, а в его середине практически равна нулю. Направлением магнитных силовых линий считается направление от севера к югу.
Ошибочно считать, что магнитные силовые линии начинают свое движение от северного полюса и заканчивают свой век на южном. Это не так. Магнитные линии — они замкнуты и непрерывны. В магните это будет выглядеть примерно так.

Если приблизить два разноименных полюса, то произойдет притягивание магнитов

Если же приблизить одноименными полюсами, то произойдет их отталкивание

Итак, ниже важные свойства магнитных силовых линий.
- Магнитные линии не поддаются гравитации.
- Никогда не пересекаются между собой.
- Всегда образуют замкнутые петли.
- Имеют определенное направление с севера на юг.
- Чем больше концентрация силовых линий, тем сильнее магнитное поле.
- Слабая концентрация силовых линий указывает на слабое магнитное поле.
Магнитные силовые линии, которые образуют магнитное поле, называют также магнитным потоком.
Итак, давайте рассмотрим два рисунка и ответим себе на вопрос, где плотность магнитного потока будет больше? На рисунке «а» или на рисунке «б»?

Видим, что на рисунке «а» мало силовых магнитных линий, а на рисунке «б» их концентрация намного больше. Отсюда можно сделать вывод, что плотность магнитного потока на рисунке «б» больше, чем на рисунке «а».
В физике формула магнитного потока записывается как

Ф — магнитный поток, Вебер
В — плотность магнитного потока, Тесла
а — угол между перпендикуляром n (чаще его зовут нормалью) и плоскостью S, в градусах
S — площадь, через которую проходит магнитный поток, м 2

Что же такое 1 Вебер? Один вебер — это магнитный поток, который создается полем индукцией 1 Тесла через площадку 1м 2 расположенной перпендикулярно направлению магнитного поля.
Напряженность магнитного поля
Формула напряженности
Слышали ли вы когда-нибудь такое выражение: «напряженность между ними все росла и росла». То есть по сути напряженность — это что-то невидимое, какая-то сдерживающая сила, энергия. Здесь почти все то же самое. Напряженностью магнитного поля также часто называют силой магнитного поля. Напряженность магнитного поля напрямую зависит от плотности магнитного потока и выражается формулой
H — напряженность магнитного поля, Ампер/метр
B — плотность магнитного потока, Тесла
μ0 — магнитная постоянная = 4π × 10 -7 Генри/метр или если написать по человечески 1,2566 × 10 -6 Генри/метр.
Эта формула работает только тогда, когда между витками катушки находится воздух, либо вакуум. Более крутая формула выглядит вот так.
μ — это относительная магнитная проницаемость.
У разных веществ она разная

Напряженность магнитного поля проводника с током
Итак, имеем какой-либо проводник, по которому течет электрический ток.

Для того, чтобы вычислить напряженность магнитного поля на каком-то расстоянии от проводника при условии, что проводник находится в воздушном пространстве либо в вакууме, достаточно воспользоваться формулой
I — сила тока, текущая через проводник, Ампер
r — расстояние до точки, в которой измеряется напряженность, метр
Магнитное поле проводника с током
Оказывается, если через какой-либо проводник пропустить электрический ток, то вокруг проводника образуется магнитное поле.

Здесь можно вспомнить знаменитое правило буравчика, но для наглядности я лучше буду использовать правило самореза, так как почти все хоть раз в жизни ввинчивали либо болт, либо саморез.
Ввинчиваем по часовой стрелке — саморез идет вниз. В нашем случае он показывает направление электрического тока. Движение наших рук показывает направление линий магнитного поля. Все то же самое, когда мы начинаем откручивать саморез. Он начинает вылазить вверх, то есть в нашем случае показывает направление электрического тока, а наша рука в этом время рисует в воздухе направление линий магнитного поля.
Также часто в учебниках физики можно увидеть, что направление электрического тока от нас рисуют кружочком с крестиком, а к нам — кружочком с точкой. В этом случае опять представляем себе саморез и уже в голове увидим направление магнитного поля.

Как думаете, что будет если мы сделаем вот такую петельку из провода? Что изменится в этом случае?

Давайте же рассмотрим этот случай более подробно. Так в этой плоскости оба проводника создают магнитное поле, то по идее они должны отталкиваться друг от друга. Но если они хорошо закреплены, то начинается самое интересное. Давайте рассмотрим вид сверху, как это выглядит.

Как вы можете заметить, в области, где суммируются магнитные силовые линии плотность магнитного потока прям зашкаливает.
Соленоид
А что если сделать много-много таких петелек? Взять какую-нибудь круглую бобину, намотать на нее провод и потом убрать бобину. У нас должно получится что-то типа этого.
Если подать постоянное напряжение на такую катушку, магнитные силовые линии будут выглядеть вот так.

Вы только посмотрите, какая бешеная плотность магнитного потока внутри такой катушки! Получается, что от каждой петельки магнитное поле суммируется, что в итоге дает такую плотность магнитного потока. Такую катушку также называют катушкой индуктивности или соленоидом.
Вот также схема, показывающая как магнитные силовые линии складываются в соленоиде.

Плотность магнитного потока зависит от того, какая сила тока проходит через соленоид. Чтобы увеличить плотность магнитного потока, достаточно поверх витков намотать еще больше витков и вставить сердечник из специального материала — феррита.

Если в электрических цепях есть такое понятие, как ЭДС — электродвижущая сила, то и в магнитных цепях есть свой аналог — МДС — магнитодвижущая сила. Магнитодвижущая сила выражается в виде тока, протекающего через катушку из N витков и выражается в Амперах-витках.

I — это сила тока в катушке, Амперы
N — количество витков катушки, штуки)
Также советую посмотреть очень простое и интересное видео про магнитное поле.
Представление о магнитном поле
Мы все знаем, что такое постоянные магниты. Магниты – это металлические тела, притягивающиеся к другим магнитам и к некоторым металлам. То, что располагается вокруг магнита и взаимодействует с окружающими предметами (притягивает или отталкивает некоторые из них), называется магнитным полем.
Источником любого магнитного поля являются движущиеся заряженные частицы. А направленное движение заряженных частиц называется электрическим током. То есть, любое магнитное поле вызывается исключительно электрическим током.
За направление электрического тока принимают направление движения положительно заряженных частиц. Если же движутся отрицательные заряды, то направление тока считается обратным движению таких зарядов. Представьте себе, что по кольцевой трубе течет вода. Но мы будем считать, что некий «ток» при этом движется в противоположном направлении. Электрический ток обозначается буквой I.
В металлах ток образуется движением электронов – отрицательно заряженных частиц. На рисунке ниже, электроны движутся по проводнику справа налево. Но считается, что электрический ток направлен слева направо.

Это произошло потому, что когда начали изучение электрические явления, не было известно, какими именно носителями чаще всего переносится ток.
Если мы посмотрим на этот проводник с левой стороны, так, чтобы ток шел «от нас», то магнитное поле этого тока будет направлено вокруг него по часовой стрелке.
Если рядом с этим проводником расположить компас, то его стрелка развернется перпендикулярно проводнику, параллельно «силовым линиям магнитного поля» — параллельно черной кольцевой стрелке на рисунке.
Если мы возьмем шарик, имеющий положительный заряд (имеющий дефицит электронов) и бросим его вперед, то вокруг этого шарика появится точно такое же кольцевое магнитное поле, закручивающееся вокруг него по часовой стрелке.
Ведь здесь тоже имеет место направленное движение заряда. А направленное движение зарядов есть электрический ток. Если есть ток, вокруг него должно быть магнитное поле.
Движущийся заряд (или множество зарядов – в случае электрического тока в проводнике) создает вокруг себя «тоннель» из магнитного поля. Стенки этого «тоннеля» «плотнее» вблизи движущего заряда. Чем дальше от движущегося заряда, тем слабее напряженность («сила») создаваемого им магнитного поля. Тем слабее реагирует на это поле стрелка компаса.
Закономерность распределение напряженности магнитного поля вокруг его источника такая же, как закономерность распределения электрического поля вокруг заряженного тела – она обратно пропорциональна квадрату расстояния до источника поля.
Если положительно заряженный шарик перемещается по кругу, то кольца магнитных полей, образующихся вокруг него по мере его движения, суммируются, и мы получим магнитное поле, направленное перпендикулярно плоскости, в которой перемещается заряд:
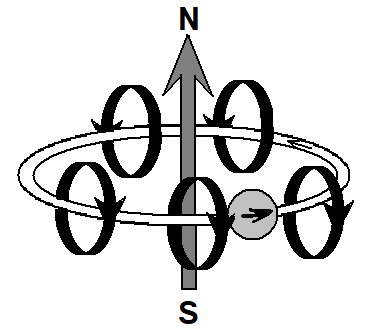
Магнитный «тоннель» вокруг заряда оказывается свернутым в кольцо и напоминает по форме тор (бублик).
Такой же эффект получается, если свернуть в кольцо проводник с током. Проводник с током, свернутый в многовитковую катушку называется электромагнитом. Вокруг катушки складываются магнитные поля движущихся в ней заряженных частиц — электронов.
А если заряженный шарик вращать вокруг его оси, то у него появится магнитное поле, как у Земли, направленное вдоль оси вращения. В данном случае током, вызывающим появление магнитного поля, является круговое движение заряда вокруг оси шарика – круговой электрический ток.

Здесь, по сути, происходит то же самое, что и при движении шарика по кольцевой орбите. Только радиус этой орбиты уменьшен до радиуса самого шарика.
Все сказанное выше справедливо и для шарика заряженного отрицательно, но его магнитное поле будет направлено в противоположную сторону.
Данный эффект был обнаружен в опытах Роуланда и Эйхенвальда. Эти господа регистрировали магнитные поля вблизи вращающихся заряженных дисков: рядом с этими дисками начинала отклоняться стрелка компаса. Направления магнитных полей в зависимости от знака заряда дисков и направления их вращения, показаны на рисунке:
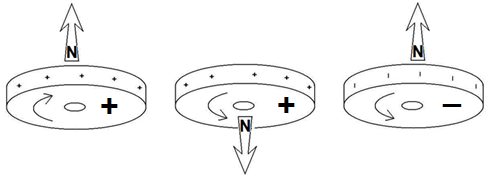
При вращении незаряженного диска, магнитные поля не обнаруживались. Не было магнитных полей и вблизи неподвижных заряженных дисков.
Модель магнитного поля движущегося заряда
Чтобы запомнить направление магнитного поля движущегося положительного заряда, мы представим себя на его месте. Поднимем правую руку вверх, затем укажем ею направо, затем опустим ее вниз, затем укажем влево и вернем руку в исходное положение – вверх. Затем повторим это движение. Наша рука описывает круги по часовой стрелке. Теперь начнем движение вперед, продолжая вращать рукой. Движение нашего тела – аналог движения положительного заряда, а вращение руки по часовой стрелке – аналог магнитного поля заряда.
Теперь представьте себе, что вокруг нас находится тонкая и прочная эластичная паутина, похожая на струны пространства, которые мы рисовали, создавая модель электрического поля.

Когда мы движемся сквозь эту трехмерную «паутину», из-за вращения руки, она, деформируясь, смещается по часовой стрелке, образуя подобие спирали, словно бы наматываясь в катушку вокруг заряда.
Сзади, за нами, «паутина» восстанавливает свою правильную структуру. Примерно так можно представлять себе магнитное поле положительного заряда, движущегося прямо.
А теперь попробуйте двигаться не прямо вперед, а по кругу, например, поворачивая при ходьбе налево, при этом вращая рукой по часовой стрелке. Представьте себе, что вы движетесь через нечто, напоминающее желе. Из-за вращения вашей руки, внутри круга, по которому вы движетесь, «желе» будет смещаться вверх, образуя горб над центром круга. А под центром круга, образуется впадина из-за того, что часть желе сместилось вверх. Так можно представлять себе формирование северного (горб сверху) и южного (впадина снизу) полюсов при движении заряда по кольцу или его вращения.
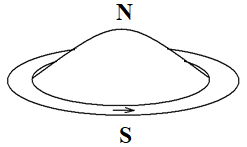
Если при ходьбе вы будете поворачивать направо, то «горб» (северный полюс) сформируется снизу.
Аналогично можно сформировать представление о магнитном поле движущегося отрицательного заряда. Только вращать рукой нужно в противоположную сторону – против часовой стрелки. Соответственно, магнитное поле будет направлено в противоположную сторону. Просто каждый раз следите за тем, в какой сторону ваша рука выталкивает «желе».
Такая модель наглядно демонстрирует то, почему северный полюс одного магнита притягивается к южному полюсу другого магнита: «горб» одного из магнитов втягивается во «впадину» второго магнита.
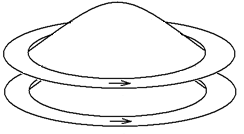
И еще эта модель показывает, почему не существуют отдельных северных и южных полюсов магнитов, как бы мы их не разрезали – магнитное поле представляет собой вихревую (замкнутую) «деформацию пространства» вокруг траектории движущегося заряда.
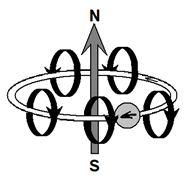
У электрона было обнаружено магнитное поле, такое, какое у него должно быть в том случае, если бы он был шариком, вращающимся вокруг своей оси. Это магнитное поле назвали спином (от английского to spin — вращаться).
Кроме того, у электрона существует еще и орбитальный магнитный момент. Ведь электрон не только «вращается», но движется по орбите вокруг ядра атома. А движение заряженного тела порождает магнитное поле. Так как электрон заряжен отрицательно, магнитное поле, вызванное его движением по орбите, будет выглядеть так:
Если направление магнитного поля, вызванного движением электрона по орбите, совпадает с направлением магнитного поля самого электрона (его спином), эти поля складываются и усиливаются. Если же эти магнитные поля направлены в разные стороны, они вычитаются и ослабляют друг друга.
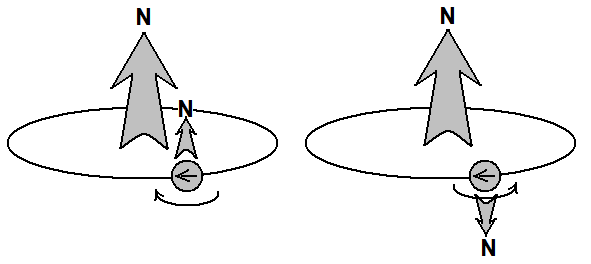
Кроме того, могут суммироваться или вычитаться друг из друга магнитные поля других электронов атома. Этим объясняется наличие или отсутствие магнетизма (реакции на внешнее магнитное поле или наличие собственного магнитного поля) некоторых веществ.
UPD: Материал предназначен, в первую очередь, для школьников средних классов. Возможно, Хабр не место для подобных вещей, Но где место? Нет его.
Магнитные рекорды
Сегодня поговорим о рекордных магнитах и немного о том, зачем они нужны.

Магниты такой конструкции (резистивные биттеровские магниты) остаются рабочими лошадками лабораторий сильных магнитных полей.
Основным потребителем самых сильных магнитов весь 20 век была наука. Термоядерные установки, ускорители, исследования на базе ядерного магнитного резонанса, нейтронная физика, охлаждение до температур ниже 1 кельвина и много еще чего требует как можно большего значения магнитной напряженности/индукции (при рассмотрении «силы» поля, можно считать эти величины синонимами).
Еще одним рекордным магнитом, о котором мы сегодня говорить не будем, является двойной диполь ускорителя БАК — из 1232 таких набрано его основное кольцо. Поле ~9 Т создается сверхпроводящим кабелем из NbTi охлажденным до 1,8К
Прежде чем перейти к конкретным конструкциям, стоит вспомнить, что энергия магнитного поля, сила его воздействие на электрические заряды и диамагнетики зависит от индукции B как квадрат. Т.е. поле в 10 Тесла несет в 100 больше энергии, чем поле в 1 Тесла. При этом важной характеристикой является давление поле на токовые трубки, которое равно 4 B^2 атмосфер. Т.е. для конструктора магнита поле в 100 Т эквивалетно попытке создать баллон на 40000 атмосфер — крайне непростая задача. Отсюда же видно, что мощные магниты с большим рабочим объемом (как у ИТЭР) — это еще большая сложность, чем просто мощные магниты.

Еще одним необычным рекордом являются сверхпроводящие магниты немецкого стелларатора Wendelstein 7-X со сложнейшей геометрией.
Итак, начнем мы с определения некоторых координат. Для постоянных магнитов, которые выпускает промышленность, характерны значения поля от 0,01 до 0,5 Т, причем неодимовые магниты в 0,5 Т уже воспринимаются как “сильные”. Рекорд, который можно выжать из постоянных магнитов ~1,5 Т у самой поверхности.
Довольно оригинальным применением силы неодимовых магнитов является 19 кВт электродвигатель (на снимке — красный цилиндр), 2 таких крутят насосы окислителя и горючего на новом ракетном двигателе «Резерфорд» компании Rocket lab.
Где-то начиная с 1,5 Т обычные медные электромагниты начинают испытывать трудности, прежде всего с отводом тепла. Необходимость перемежать медь с трубками водяного охлаждения, а также растущее межвитковое напряжение вздувает размеры магнита гораздо быстрее, чем растет поле. Витки, которые располагаются дальше от рабочего объема вносят относительно небольшой вклад в поле, а значит ток в основном расходуется на нагрев магнита, а не на создание поля.
Медь
Однако с 1930х годов и почти до сих пор рекордные стационарные поля достигались в практически обычных водоохлаждаемых медных магнитах. Это так называемые Биттеровские магниты, представляющие собой медную пластинку свитую в спираль и имеющую хитрую систему продольных каналов охлаждения. Для этих магнитов характерны чудовищные плотности тока (до 700 А/мм^2), электрические мощности в 1,10 и даже 30 мегаватт, и расход охлаждающей воды в десятки и сотни литров в секунду. Первый магнит на 10 Т был пущен в 1936 году, и следующие 30 лет держал рекорд по стационарному полю.
Американские биттеровские магниты 60-х годов на 25 Тесла.
Эта конструкция магнитов затем неоднократно оптимизировалась, и на сегодня рекорд поля в таких магнитах доведен до 38,5 Т в китайской лаборатории CHMFL. Мощность магнита составила 28,5 МВт с расходом охлаждающей воды в 500 литров в секунду (кстати, похоже к мощности магнита надо добавить еще примерно такую же на насосы, которые прокачивают эту воду через магнит). Ток около 36 тысяч ампер. При этом рекордное поле достигается в объеме диаметром всего 32 мм и длинной около 70 мм.
Китайский рекордный резистивный магнит — один заход спирали соленоида (из сплава CuAg), разрез и набор коаксиальных катушек.
Резистивные магниты сегодня подошли к лимитам возможностей материалов, и максимальное доступное поле в них растет в основном экстенсивно — за счет наращивания мощности системы питания и охлаждения, увеличения количества катушек. Подобные магниты сегодня в основном используются для изучения очень разнообразных физических явлений в небольших образцах, зачастую при низкой температуре. Поэтому такие магниты работают в центрах коллективного использования, когда физики привозят свои образцы и аппаратуру, устанавливают ее на магнит и измеряют нужные им величины. Для маленьких образцов вполне удобно использовать магниты с небольшим просветом, типа 20-30 мм.
Верхушка биттеровского магнита на 30 Т без крышки. Здесь видно отверстие исследовательской камеры и щели для подачи охлаждающей воды.
Однако есть еще одно применение больших магнитных полей сегодня — это ЯМР-томография, т.е. построение карт плотности тканей за счет взаимодействия водорода с радиоизлучением в сильном магнитном поле. Чем выше поле — тем большее пространственное разрешение системы. Для таких систем нужен довольно большой рабочий объем магнита а также высокая гомогенность поля. Исследования в области сверхпроводимости в свою очередь требуют криостатов, которые с трудом помещаются в диаметр 32 мм, да и поле для некоторых сверхпроводников нужно больше.
Немножко забегая вперед — сверхпроводящий ЯМР-томограф со сверхвысоким полем (21Т), просветом 110 мм и пример получаемого изображения с разрешением в 26 мкм
Поэтому с 80х годов 20 века появляется направление гибридных магнитов, идея которых заключается в том, чтобы поместить биттеровский магнит внутрь сверхпроводящего, поля которых сложатся. Это позволяет поднимать поле и дальше без роста и без того монструозных требований по мощности и расходу охлаждающей воды.
Вставка магнита Биттера внутрь сверхпроводящего означает, что последний должен иметь рабочий просвет в 400-800 мм, т.е. значительно больше, чем рекорды, которые мы видели до этого. Магниты с большими рабочими объемами но меньшим полем пришли в лаборатории сильных магнитных полей от разработчиков токамаков, где в конце 70х были созданы сверхпроводящие магниты на основе холодных сверхпроводников — ниобата олова и титана. В середине 80х в французской лаборатории сильных магнитных полей LNCMI создают гибридный магнит из 11Т сверхпроводящего и 22Т биттеровского с общим полем в 31Т, а в 2000 году американская National MagLab запускает установку гибридом с полем в 45Т, которая является рекордной до сих пор среди всех магнитов с постоянным полем.
Корпус всего магнита (слева) и криостата (справа)
Разрез гибридного магнита по криостату. Кстати, конструкция внешнего сверхпроводящего магнита, спроектированная для этой установки затем была использована еще в трех рекордных магнитах.
45 тесловый гибрид использует три внешних сверхпроводящих магнита и 4 внутренних резистивных типа “Биттер-флорида”. Резистивная часть потребляет 29 мегаватт при токе 74 кА и создает поле в 31 Т. Сверхпроводящая часть магнита создает поле в 14 Т и состоит из внешних обмоток из NbTi и внутренних из Nb3Sn, работает на токе в 8 кА при температуре 4,2 К. Просвет криостата сверхпроводящего магнита — 500 мм.
Сверхпроводящий внешний магнит гибрида на 45Т
И внутренний биттеровский магнит. Так 2,5 метра корпуса превращается в 32 мм рабочей камеры.
Для сравнения, напомню, что тороидальный магнит ИТЭР имеет ток проводинка в 68 кА, поле 12,8 Т при просвете 9000х7000 мм, т.е. можно представить, насколько далеко ИТЭР двинул вперед технологии низкотемпературных сверхпроводящих магнитов.
Кстати, в лабораторных магнитах используют проводник с гораздо меньшим током, наматывая больше витков — это упрощает систему питания да и сам проводник. Обратной стороной этого является бОльшие электрические напряжения в системе, когда сверхпроводник внезапно переходит в нормальное состояние.
Кроме ИТЭР эти технологии двинулись вперед с появлением промышленных высокотемпературных сверхпроводников. Если низкотемпературные СП в принципе не позволяют создать поля выше 22 Т, т.е. они могут быть только частью рекордного магнита, то для ВТСП этот лимит расширяет до как минимум 45 Т.
Зависимость критической плотности тока от поля у разных сверхпроводников. Кстати, вы задумывались когда-нибудь, что за оборудование используется для построения этих диаграмм и почему они упираются в 45Т?
Сегодня новое направление создания рекордных магнитов — это полностью сверхпроводящие и сейчас все ведущие лаборатории мира (Китай, Нидерланды, Франция, США)проектируют СП-магниты на 30+ Т. Здесь тоже пока впереди всех флоридская MagLab, где началась сборка полностью сверхпроводящего магнита на 32 Т. Здесь 15 Т будет создаваться внешними магнитами из NbTi и Nb3Sn, а еще 17 — двухслойным ВТСП магнитом из YBCO лент. “Высокотемпературные” сверхпроводники здесь используются как имеющие гораздо более высокие критические поля при температуре жидкого гелия, чем “низкотемпературные”.
Проект полностью сверхпроводящего магнита на 32Т
Технологии данного магнита потребовали почти 10 лет разработок, основные проблемы лежали в области очень высоких пондеромоторных сил со стороны мощного магнитного поля на витки с током. Механические напряжение в YBCO катушках достигает 700 МПа — здесь, кстати, хорошо помогает то, что ВТСП-лента по сути в основном состоит из никелевого сплава с высокими прочностными характеристиками — медь такие напряжения не выдерживает.
НИОКР высокопольного ВТСП магнита.
Второй класс проблем связан с аварийной потерей сверхпроводящего состояния, и вывода тока из катушек. В частности, чтобы избежать пережога из-за медленного распространения нормальной зоны в катушки встроены нагреватели, которые при обнаружении перехода прогревают всю катушку, так чтобы энергия поля выделялась более равномерно.

Буквально недавно была изготовлена внутренняя рабочая катушка из ВТСП ленты, скоро можно ожидать запуска и сборки магнита.
Этот магнит будет обладать “холодным” рабочим объемом, и хорошо подойдет для изучения конденсированных состояний материи и квантовых эффектов в твердом теле, при этом по эксплуатационным расходам это совершенно другой класс устройств, в частности криостат, система криоснабжения и внешний СП-магнит из НТСП являются серийными изделиями, выпускаемымим фирмой Oxford Instruments.
Вообще oxford instruments — крупнейший поставщик сверхпроводящих магнитов, в основном для всякого научно-лабораторного применения на поля 3-15Т. В проекте ИТЭР эта фирма, например, поставляет магниты на 6Т для гиротронов
Вообще прежде чем перейти к следующим рекордсменам, хочется сказать о нескольких применениях таких магнитов за пределами просто предоставления стенда с высоким магнитыми полем.
Одним из основных прикладных потребителей серийных высокополевых магнитов являются ЯМР-спектрометры, рабочий инструмент химиков. Фирма Bruker, в частности, серийно производит спектрометры с полем до 23,5Т (у таких установок, кстати, есть довольно большие проблемы с экранированием такого поля от окружающих людей и предметов).
Исторический рост частоты ЯМР-спектрометров, что позволяет улучшать качество ЯМР-спектров.
Вторым серийным потребителем являются ЯМР-томографы высокого разрешения, которые применяются в биологических и нейробиологических исследованиях. Здесь поля доходят до 21Т. Наконец, чуть менее прикладным потребителем являются центры с нейтронными источниками, один из методов исследования магнитно-квантовых явлений — это изучение рассеяния нейтронов на материи в сильном магнитном поле, а также холодильники для субмикрокельвиновых температур, требующие полей от 8 до 20 Т.
Видео со сборки 26Т магнита с большим просветом для исследования рассеиния поляризованных нейтронов на материи в Helmholtz-Zentrum Berlin
Импульсные магниты
Основные инженерные проблемы создания высокопольных магнитов — теплоотвод и прочность — сильно облегчаются, если перейти от постоянного магнитного поля к импульсному. В свою очередь импульсные системы делятся на многоразовые и одноразовые :)
Интересно, что пионером в области импульсных магнитов был Петр Капица, занимавшийся подобными установками в 20х годах в лаборатории Кавендиша в Англии. Замыкая выход большого вращающегося генератора на соленоид он получал до 50 Т в течении нескольких миллисекунд. Такой подход позволял измерять многие величины связанные с большими магнитными полями даже в 20х, а с современной регистрирующей техникой вообще можно назвать такое поле почти квазистационарным.

Капица и его машина для создания импульсных магнитных полей.
Улучшая данный подход, в 60х разработчики переключились с вращающихся электромеханических источников энергии на конденсаторы и генераторы импульсов напряжения, позволяющие создать в медной катушке плотность тока во многие килоамперы на мм^2.
В сочетании с силовым подкреплением в виде стальной матрицы и захолаживанием жидким азотом (для снижения сопротивления, что уменьшает потребное напряжение, что облегчает изоляцию в таком магните) в 2012 году импульсные медные магниты достигли 101,2 Т в течении 1 миллисекунды — это значение на сегодня является рекордом (и принадлежит оно коллаборации американской ядерной оружейной лаборатории LANL и флоридской MagLab).
Видео про достижение рекордного значения поля в 101,2 Т. Впрочем, видно тут мало что, да и вообще такое ощущение, что конструкция магнита засекречена, известны только общие значения
Такое значение достигается также с помощью нескольких вложенных катушек, внешние из которых дают длинный импульс (около 2 секунд) амплитудой до 45 Т, а внутренние — короткий импульс в 65 Т. Такая схема позволяет выдерживать напряжения в проводнике за пределом текучести материалов.
Интересно, что мощность такого магнита достигает нескольких гигаватт.
Генератор, который закорачивают на внешние обмотки магнита для получения рекордных импульсных полей.
К сожалению, пока не видно каких-то путей по заметному увеличению значения поля в многоразовой установке. Однако если разрушение установки нам не страшно, то 101 Т — далеко не предел.
Самым простым вариантом тут является кусок меди, свернутый в виток, на который подключается высоковольтные конденсаторы. Такая схема позволяет получить и 300 и 400 тесла, правда на очень короткое время (порядка микросекунды) в объеме нескольких кубических миллиметров, что для экспериментатора, который занимается изучением топологии поверхностей Ферми в твердых телах, например, является довольно сложными ограничениями.
Импульс поля на одноразовом магните.
Довольно элегантный выход из этих ограничений был найден еще в 50х годах путем изобретения взрывомагнитных генераторов. Здесь затравочное магнитное поле в 10-20 Т сжимается до 2800 (!)Т. Делается это с помощью металлического цилиндрического лейнера, который с помощью цилиндрической взрывной волны от заряда взрывчатки коллапсирует к своей оси. При этом продольное магнитное поле увеличивается примерно в 100-200 раз. По сравнению с предыдущей схемой во взрывомагнитном генераторе можно получить чуть большее время импульса магнитного поля, и чуть бОльший объем для образца, правда ценой гораздо более сложной постановки эксперимента.

Взрывомагнитный генератор и его принципиальная схема.
Еще в 50х годах с помощью ВМГ были измерены разнообразные характеристики материалов в экстремальном магнитном поле — проводимость, вращение поляризации (эффект фарадея), сжатие магнитного поля ядра атома и т.п. Еще одним интересным результатом является возможность ускорения такими магнитными полями металлических объектов до скоростей порядка 100 км/с.
Ограничения по полю у взрывомагнитных генераторов в свою очередь опять довольно фундаментально и связано с давлением магнитного поля, которое достигает десятков мегабар и останавливает металлический лейнер. 3000 тесла тут видимо является асимпотическим пределом.
В свою очередь, бОльшие значения давления (гигабары) достигаются в установках лазерной имплозии, и чисто теоретически такие установки способны создать магнитные поля в десятки тысяч и даже 100 тысяч тесла, правда в течении наносекунд и в микронных объемах. Сам сфокусированный лазерный импульс от петаваттного лазера имеет переменное магнитное поле амплитудой еще больше — миллион тесла и выше. Конечно, условия, в которых возникает такое поле (плотная плазма температурой в сотни эВ — десятки кэВ) далеки от интересов прикладной науки, но весьма интересны науке фундаментальной.
История рекордов магнитного поля для разных типов установок (многоразовых :))
Завершая обзор магнитных рекордов стоит вспомнить про магнетары — молодые нейтронные звезды с высокими магнитными полями. Высокие здесь — это до 100 миллиардов Тесла. Магнитное поле такого порядка, к примеру обладает плотностью энергии в 10^25 Дж на кубический метр, эквивалент mc^2 для вещества в 10000 раз плотнее свинца. Наблюдения за магнетарами (и обычными нейтронными звездами, поля которых в тысячи раз меньше) позволяют лучше понять поведения материи и пространства в подобных условиях, дополняя лабораторные исследования рекордными магнитами.
Читайте также:
