Расчетное сопротивление угловых швов срезу по металлу границы сплавления

Обновлено: 05.01.2025

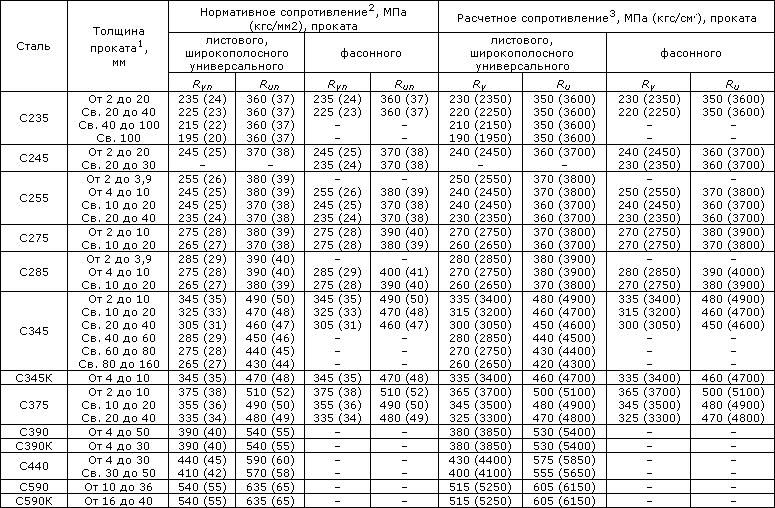
Значения нормативных и расчетных сопротивлений при растяжении, сжатии и изгибе листового, широкополосного универсального проката и труб приведены в таблице В.3, фасонного проката - в таблицах В.4 и В.5 (приложение В).

Значения расчетных сопротивлений проката смятию торцевой поверхности, местному смятию в цилиндрических шарнирах и диаметральному сжатию катков приведены в таблице В.6 (приложение В).

6.2 Расчетные сопротивления гнутых профилей следует принимать равными расчетным сопротивлениям листового проката, из которого они изготовлены.

6.3 Значения расчетных сопротивлений отливок из углеродистой стали следует принимать по таблице В.7 (приложение В).

6.4 Расчетные сопротивления сварных соединений для соединений различных видов и напряженных состояний следует определять по формулам, приведенным в таблице 4.

Примечание - Значения коэффициентов надежности по металлу шва следует принимать равными: 1,25 - при 490 Н/мм ; 1,35 - при 590 Н/мм .

Расчетное сопротивление сварного стыкового соединения элементов из сталей с разными нормативными сопротивлениями следует принимать как для стыкового соединения из стали с меньшим значением нормативного сопротивления.

Значения нормативных и расчетных сопротивлений металла угловых швов приведены в таблице Г.2 (приложение Г).

6.5 Расчетные сопротивления одноболтового соединения следует определять по формулам, приведенным в таблице 5.

Значения нормативных и расчетных сопротивлений срезу и растяжению стали болтов в одноболтовых соединениях приведены в таблице Г.5, а смятию элементов, соединяемых болтами, в таблице Г.6 (приложение Г).

Значения расчетных сопротивлений растяжению фундаментных болтов приведены в таблице Г.7 (приложение Г).

Расчетное сопротивление растяжению U-образных болтов , указанных в 5.8, следует определять по формуле

6.7 Расчетное сопротивление растяжению высокопрочных болтов, классов прочности не менее 10.9, следует определять по формуле

6.8 Расчетное сопротивление растяжению высокопрочной стальной проволоки , применяемой в виде пучков или прядей, следует определять по формуле

6.9 Значение расчетного сопротивления (усилия) растяжению стального каната следует принимать равным значению разрывного усилия каната в целом, установленному НД на стальные канаты, деленному на коэффициент надежности по материалу =1,6.

7 Расчет элементов стальных конструкций при центральном растяжении и сжатии

7.1 Расчет элементов сплошного сечения

7.1.1 Расчет на прочность элементов из стали с нормативным сопротивлением 440 Н/мм при центральном растяжении или сжатии силой N следует выполнять по формуле

Расчет на прочность растянутых элементов, эксплуатация которых возможна и после достижения металлом предела текучести, а также растянутых или сжатых элементов из стали с нормативным сопротивлением >440 Н/мм следует выполнять по формуле (5) с заменой значения на .

7.1.2 Расчет на прочность сечений в местах крепления растянутых элементов из одиночных уголков, прикрепляемых одной полкой болтами, следует выполнять по формуле (5), а сечений растянутого одиночного уголка из стали с пределом текучести до 380 Н/мм , прикрепляемого одной полкой болтами, поставленными в один ряд по оси, расположенной на расстоянии не менее 0,5b (b - ширина полки уголка) от обушка уголка и не менее 1,2d (d - диаметр отверстия для болта с учетом положительного допуска) от пера уголка, по формуле

Расчет угловых сварных швов на прочность, общие положения

Расчет угловых сварных швов на прочность обязателен при любом напряженно- деформированном состоянии элемента. Как уже отмечалось при рассмотрении основных видов сварных швов, и при растяжении, и сжатии, и при изгибе, и в любом другом напряженном состоянии рассматриваемого элемента конструкции на одном из катетов углового сварного шва всегда будут действовать касательные напряжения.

При этом на второй катет сварного шва могут действовать растягивающие (сжимающие) нормальные напряжения и (или) касательные напряжения в зависимости от напряженно деформированного состояния рассматриваемого элемента конструкции и положения шва в пространстве.

В целом основные положения, принимаемые при расчете угловых сварных швов, такие же как и при расчете остальных элементов конструкции.

Так как сопротивление металла сдвигу или срезу при действии касательных напряжений значительно меньше сопротивления растяжению, сжатию или изгибу при действии нормальных напряжений, то расчет угловых сварных швов (расчет на условный срез) сводится к определению касательных напряжений, которые должны быть меньше расчетного сопротивления.

Предполагается, что разрушение углового сварного шва может произойти в двух плоскостях: по металлу шва и по границе сплавления, поэтому расчет угловых швов производится для этих двух сечений:

Рисунок 529.3. Расчетные сечения угловых швов

А теперь рассмотрим возможные напряженные состояния элементов, соединяемых угловыми швами, более подробно.

Расчет угловых сварных швов производится по следующим формулам:

1. Расчет угловых швов при центральном растяжении (рисунок 529.2.д)) или сжатии (действии силы N)

Рисунок 529.2. Основные виды сварных соединений с угловыми швами.

И лобовые и фланговые швы рассчитываются на условный срез

1.1. по металлу шва (сечение 1 на рисунке 529.3):

где N - значение продольной растягивающей (или сжимающей) силы, приложенной по оси, совпадающей с центром тяжести сечения (без эксцентриситета). Может измеряться в кгс, тс, Н, кН;

β_f - безразмерный коэффициент, определяемый по следующей таблице:

Таблица 529.2. (согласно СНиП II-23-81* "Стальные конструкции")

Примечание: почему при расчетах я рекомендую пользовать именно этой таблицей, а не таблицей из актуализированной редакции указанного СНиПа, достаточно подробно объясняется в статье, посвященной рассмотрению основных видов сварных швов.

k_f - катет углового шва. Принимается по конструктивным требованиям или согласно расчету. Измеряется в мм или см.

l_w - суммарная длина угловых швов с учетом непровара в начале и в конце шва. Например, если рассчитывается один угловой шов длиной l, то его расчетная длина составит:

l_w = l - 2t (529.1.1)

где t - толщина наименьшей из свариваемых деталей.

В целом произведение β_fk_fl_w - это и есть площадь рассматриваемого сечения.

R_wf - расчетное сопротивление срезу по металлу шва. Определяется по следующей таблице:

Таблица 530.2. Расчетные сопротивления сварных соединений (согласно СП 16.13330.2011 "Стальные конструкции")

Примечания:

1. Значения коэффициентов надежности по металлу шва γ_wm следует принимать:

γ_wm = 1,25 - при R_wun ≤ 490 Н/мм 2 (4900 кг/см 2 );

γ_wm = 1,35 - при R_wun ≥ 590 Н/мм 2 (5900 кг/см 2 )

Значения R_wun и R_f определяются по следующей таблице:

Таблица 531.1. (согласно СП 16.13330.2011 "Стальные конструкции")

Примечание:

В ныне неактуальном СНиП II-23-81* и старых справочниках, таблица вида 530.2 сопровождалась следующими примечаниями:

1. Для угловых швов, выполняемых ручной сваркой, значения R_wun принимают равными значениям временного сопротивления разрыву металла шва (σ_в) согласно ГОСТ 9467-75*.

Приводить здесь таблицу из ГОСТа, по которой можно определить временное сопротивление разрыву шва, я не буду. Просто скажу, что в маркировке электродов это значение уже указано в кгс/мм 2 . Например:

- для электродов Э38 R_wun = σ_в = 38 кгс/мм 2 (3800 кгс/см 2 )

- для электродов Э42А R_wun = σ_в = 42 кгс/мм 2 (4200 кгс/см 2 ) и так далее вплоть до Э150 (сейчас такие марки электродов даже и не рассматриваются).

На мой взгляд это учень удобно, тем не менее сейчас все принято выражать в единицах системы СИ, что и отображено в таблице 531.1.

γ_с - коэффициент условий работы элементов конструкций и соединений, принимаемый по следующей таблице:

Таблица 530.3. Коэффициенты условий работы элементов и соединений стальных конструкций (согласно СП 16.13330.2011 "Стальные конструкции")

1.2. По металлу границы сплавления (сечение 2 на рисунке 529.3):

где β_z - безразмерный коэффициент, определяемый по таблице 529.2.

R_wz - расчетное сопротивление металла на границе сплавления, определяемое по таблице 530.2, где R_un - нормативное сопротивление проката, определяемое по следующей таблице:

Таблица 171.8. (согласно ГОСТ 27772-88 для стальных конструкций зданий и сооружений)

Примечание: заменяемые марки стали приводятся отдельно.

Тут добавлю, что при центральном растяжении или сжатии элемента из свариваемых деталей во фланговых швах на обеих катетах шва будут действовать касательные напряжения. В лобовых швах на одном из катетов будут действовать растягивающие или сжимающие нормальные напряжения, имеющие такое же значение, как и касательные напряжения на втором катете.

Я это все к тому, что иногда в справочниках напряжения, определяемые для других видов напряженно-деформированного состояния обозначаются как нормальные, т.е. литерой "σ". Формально тут большой ошибки нет и делается это больше для того, чтобы различать напряжения, возникающие при действии изгибающего момента и других возможных воздействий. Но все равно нельзя забывать, что расчет производится именно на условный срез, т.е. на действие касательных напряжений, имеющих, впрочем, такое же значение, как нормальные на втором катете. А вот направления действия касательных напряжений действительно могут быть разными, что мы вскоре и увидим.

2. Расчет сварных соединений с угловыми швами при действии изгибающего момента М в плоскости, перпендикулярной плоскости расположения швов

Т.е. в данном случае имеется в виду, что через рассматриваемые швы можно провести одну плоскость и эта плоскость будет перпендикулярна плоскости действия момента. К положению плоскости, в которой может произойти разрушение шва, данная формулировка никакого отношения не имеет.

Как правило такая ситуация возникает при расчете сварного соединения втавр двухсторонними швами (рисунок 529.2.г)) или односторонними швами (рисунок 529.3). При этом угловые швы рассчитываются на условный срез

2.1. по металлу шва (сечение 1 на рисунке 529.3):

2.2. по металлу границы сплавления (сечение 2 на рисунке 529.3):

где М - значение изгибающего момента, определяемое по эпюре "М".

W_f и W_z - моменты сопротивления расчетных сечений сварного соединения по металлу шва и по границе сплавления с металлом соответственно.

Например при соединении втавр двухсторонними швами моменты сопротивления составят:

Как правило, разделив момент М на момент сопротивления W, мы определяем нормальные напряжения, поэтому в некоторых старых учебниках и справочниках (например: А.П.Мандриков, Примеры расчета металлических конструкций, М.-1991) формулы (531.3) и (531.4) имеют другую форму записи, примерно такую:

Но сути это не меняет.

1. В СНиП II-23-81* и старых справочниках значение расчетного сопротивления R_wf и R_wz при всех возможных расчетных случаях дополнительно умножалось на коэффициенты условий работы шва γ_wf или γ_wz соответственно.

Значение этих коэффициентов принималось равным 1 во всех случаях, кроме конструкций, возводимых в климатических районах I₁ (согласно ГОСТ 16350-80: очень холодный, среднемесячная температура воздуха в январе от -50 до -30), I₂ (холодный, температура от -30 до -15), II₂ (арктический восточный, температура от -28 до -18) и II₃ (арктический западный, температура от -30 до -2), для которых γ_wf = 0.8 при R_wun = 410 МПа и γ_wz = 0.85 для всех сталей.

На мой взгляд данное ограничение значения расчетного сопротивления вводилось с целью уменьшения риска хрупкого разрушения сварного соединения при низких температурах. Сейчас оно не действует, но думаю, знать о нем надо.

2. Вообще-то это примечание следовало сделать при рассмотрении первого раздела, но он и так получился перенасыщенным информацией, поэтому оставлю это примечание здесь.

3. Расчет угловых швов при действии изгибающего момента М в плоскости, перпендикулярной плоскости швов и действии продольной силы N

Подобная ситуация часто встречается при расчете разного рода опорных площадок, поэтому я выделил ее в отдельный раздел, хотя в СП 16.13330.2011 такой вариант загружения отдельно не рассматривается.

Тем не менее, при загружении опорной площадки некоторой силой, приложенной с эксцентриситетом, возникает следующая ситуация, которую я решил проиллюстрировать картинкой из все того же А.П.Мандрикова:

Рисунок 531.1.

В этом случае угловые швы рассчитываются на условный срез

3.1. по металлу шва:

3.2. по металлу границы сплавления:

где значение касательных напряжений определяется в зависимости от рассматриваемого сечения по формулам (531.1) и (531.2), а значение условно нормальных напряжений - по формулам (531.3.2) и (531.4.2) соответственно.

Конечно же согласно требований ныне действующих нормативных документов более правильно вести речь только о касательных напряжениях относительно осей х и у. Т.е. т_wf = т_y, σ_wf = т_х и так далее, но как уже говорилось, на окончательные результаты расчета это ни как не влияет, при этом старый подход выглядит более наглядным.

4. Расчет угловых швов при действии изгибающего момента М в плоскости сварных швов

Подобная ситуация часто встречается при расчете стыковых соединений с накладками, т.е. при одновременном использовании и лобовых и фланговых швов (см. рисунок 529.2.в)), а также при соединении внахлест лобовыми или фланговыми швами (см. рисунок 529.2.а) и б)). Это означает, что как и в предыдущем случае касательные напряжения действуют как вдоль оси х, так и вдоль оси у. Соответственно задача сводится к определению равнодействующей этих двух напряжений. Расчет в этом случае выполняется по следующим формулам:

4.1. по металлу шва:

4.2. по металлу границы сплавления:

где х и у - координаты рассматриваемой точки сварного соединения относительно главных осей х-х и у-у. Как правило рассматриваемая точка максимально удалена от центра тяжести О расчетного сечения.

I_fx, I_fy, I_zx, I_zy - моменты инерции рассматриваемых сечений швов относительно главных осей.

Так как рассчитываемые швы находятся в одной плоскости с действующим моментом, то для определения указанных моментов инерции необходимо кроме катета, длины шва и соответствующих коэффициентов также знать расстояние между швами, чего не требовалось при рассмотрении швов, находящихся в плоскости, перпендикулярной плоскости действия момента.

В нормативных документах вопросу определения моментов инерции для угловых сварных швов внимания не уделяется, но на мой взгляд это достаточно сложный вопрос и вообще его рассмотрению следует посвятить отдельную статью, а пока ограничимся следующим примером:

При соединении внахлест только лобовыми швами и при расстоянии между центрами тяжести лобовых швов, равном l (центры тяжести и расстояние l на рисунке 529.2.а) не показаны), значения моментов инерции для сечения металла шва составят:

5. Расчет угловых швов при действии момента М, продольной N и поперечной V сил в плоскости сварных швов

Это наиболее общий случай напряженно-деформированного состояния, проиллюстрированный в СП 16.13330.2011 следующим образом:

Рисунок 531.2. Расчетная схема сварного соединения с угловыми швами в общем случае загружения.

Расчет в этом случае выполняется по следующим формулам:

5.1. по металлу шва:

5.2. по металлу границы сплавления:

где т_f и т_z - касательные напряжения в рассматриваемой точке расчетного сечения сварного соединения по металлу шва и по металлу границы сплавления, определяемые по формуле:

где т_N и т_V - касательные напряжения, определяемые по формулам (531.1) и (531.2), а т_Мх и т_Му - горизонтальная и вертикальная составляющие касательных напряжений при действии момента, определяемые по следующим формулам:

Но и это еще не все. При проектировании строительных конструкций необходимо также соблюдать конструктивные требования, предъявляемые к сварным соединениям.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье "Записаться на прием к доктору"

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Для Украины - номер гривневой карты (Приватбанк) 5168 7422 4128 9630

Рассчитать формулу нахлесточное соединения

Доктор, как увязать формулы 531.7(8) с формулами 531.14 и 531.15. Судя по всему в знаменателе должна быть сумма моментов инерции тМх = М*х/(Iy+Ix) и тМу = М*у/(Iy+Ix). В подтверждение предлагаю книгу: Металлические конструкции (вопросы и ответы), Бирюлев В.В., страница 56

Судя по чему? Будьте добры, распишите более подробно. Можете цитировать Бирюлева В.В.

При N=0 и Q=0 формула (531.13) т = ((тN + тМх)^2 + (тV + тМу)^2)^1/2 при знаменателе (Iy+Ix) примет вид т = ((М*х/(Iy+Ix))^2 + (М*х/(Iy+Ix))^2)^1/2 и сведется к формуле (531.7) тМ = М(х^2 + у^2)^1/2/(Ix + Iy). У господина Бирюлева (книга есть на двг.ру) тxM = M*r*cos(a)/(Ify+Ifx), тyM = M*r*sin(a)/(Ify+Ifx), где r=(х^2 + у^2)^1/2, cos(a)=y/r, sin(a)=x/r, соответственно тxM = M*r*(y/r)/(Ify+Ifx), тyM = M*r*(x/r)/(Ify+Ifx). Хмм. не заметил даже, что x и y наоборот у него, так что по Бирюлеву тМх = М*y/(Iy+Ix) и тМу = М*x/(Iy+Ix)

Так уже значительно лучше. Если я правильно понял господина Бирюлева в вашем изложении, то после сокращения формул тxM = M*r*(y/r)/(Ify+Ifx), тyM = M*r*(x/r)/(Ify+Ifx) получается, что тxM = M*y/(Ify+Ifx), тyM = M*x/(Ify+Ifx), где f - это символ функции. А аргумент функции и значение функции - это вроде бы разные вещи. Поэтому ваш логический переход Ify+Ifx = Iy+Ix пока ничем не обоснован с чисто математической точки зрения. Обоснуйте.

Хорошо, avatar, развивайте свою мысль: если формулы 531.14 и 531.15 неправильные (как вы утверждаете), то значит и с остальными формулами что-то не так. Например, формула σwf = М/Wf ≤ Rwfγc (531.3.2) по вашей логике должна выглядеть так: σwf = М/(Wfх + Wfу) ≤ Rwfγc. Где ошибка?
И тут не нужны какие-то доп.картинки, формулы и примеры расчетов - это все теория, которую следует подтверждать практикой. А для научного диспута, который мы тут затеяли, вполне достаточно 4 картинок, которые есть в данной статье, общих знаний строймеха и сопромата, ну и конечно же - геометрии, без нее никуда.

Ошибка в том, что формула нормального напряжения (531.3.2) относится к напряжению от действия момента в плоскости, перпендикулярной плоскости швов, а формула касательных напряжений (531.7) - к действию момента в плоскости швов. Например, формула тМ = М(х2 + у2)1/2/(Ifx + Ify) ≤ Rwfγc (531.7) по вашей логике должна выглядеть так: тМ = ((Mx/Iy)^2 + (My/Ix)^2)^1/2 = M((x/Iy)^2 + (y/Ix)^2)^1/2. Где ошибка?
И это далеко не научный дискурс. Просто мне было интересно, откуда молодой инженер взял эти формулы.

Я деменцию бесплатно не лечу, тем более в таком запущенном состоянии. Хочешь лечиться - запишись на прием, нет - до свидания. И да, если действительно хочешь лечиться, то сначала сам разберись:
1. Вокруг какой оси вращает момент поперечное сечение шва в первом и во втором случае?
2. Чем крутящий момент отличается от изгибающего и какой более простой формулой можно заменить формулу (531.7)?
3. Что такое площадки напряжений и как суммируются нормальные и касательные напряжения на главных площадках при плоском напряженном состоянии хотя бы по первой теории прочности?
Для начала хватит. Задачку по геометрии ты решил правильно, поэтому не безнадежен.

А зачем дурик усы сбрил или откуда молодой инженер взял формулы - это ты у Петровича спроси, может он знает. Ему пациенты такие вопросы часто задают.

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье "Записаться на прием к доктору" (ссылка в шапке сайта).

ПРЕДИСЛОВИЕ

Пособие составлено к главе СНиП II-23-81. В Пособии приведен ряд новых решений, направленных на экономию основных видов ресурсов, расходуемых при выполнении сварочных работ. Основное внимание уделено рациональному проектированию сварных соединений с угловыми швами, которые составляют по массе наплавленного металла около 90 % от общего количества сварных швов. Поэтому наибольший эффект может быть получен от оптимизации размеров этих швов.

Новые нормы проектирования дают возможность сократить удельный расход наплавленного металла в строительных стальных конструкциях на 35-40 %.

Текст из главы СНиП II-23-81 отмечен в Пособии вертикальной чертой, в скобках указаны соответствующие номера пунктов и таблиц главы СНиП.

Пособие разработано ЦНИИСК им. Кучеренко (канд. техн. наук В.М. Барышев, при участии инж. Ю .А. Новикова).

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. При проектировании сварных соедине ний следует:

принимать минимально необходимое количество и минимальные размеры сварных швов;

предусматривать применение высокопроизводительных механизированных способов сварки;

предусматривать применение эффективных сварочных материалов (электродов, электродных проволок, защитных газов, флюсов);

предусматривать такое расположение и размеры сварных швов, при которых максимально сокращалась бы необходимость кантовки конструкций при их изготовлении, а также уменьшились бы размеры соединяемых деталей;

обеспечивать свободный доступ к местам наложения швов и удобное пространственное положение с учетом выбранного способа и технологии сварки и принятого метода неразрушающего контроля шва.

1.2. Сокращение массы наплавленного металла при проектировании сварных соединений и элементов конструкций достигается путем повышения расчетных сопротивлений соединений с угловыми швами за счет применения эффективной технологии сварки и электродных материалов; соблюдения требований по назначению минимально допустимых катетов угловых швов, устанавливаемых в зависимости от наибольшей толщины свариваемых элементов, вида сварки и механических свойств стали; применения односторонних угловых швов в поясах сварных двутавров, при приварке ребер жесткости, диафрагм и других деталей, а также уменьшения количества деталей в элементах конструкций или их размеров (применения односторонних ребер жесткости, исключения фасонок в решетчатых конструкциях или уменьшения их размеров в связи с повышением расчетных сопротивлений соединений с угловыми швами и др.).

1.3. При проектировании сварных соединений следует учитывать, что увеличение сечений швов по сравнению с регламентированными в главе СНиП II-23-81 не только не повышает работоспособность конструкций, но в ряде случаев снижает ее.

2. РАСЧЕТНЫЕ СОПРОТИВЛЕНИЯ СВАРНЫХ СОЕДИНЕНИЙ

2.1 (3.4). Расчетные сопротивления сварных соединений для различных видов соединений и напряженных состояний следует определять по формулам, приведенным в табл. 3 СНиП II-23-81.

2.2. Расчетные сопротивления сварных соединений, определенные по формулам, которые приведены в главе СНиП II-23-81, обеспечиваются при соблюдении следующих условий:

сварочные материалы для расчетных угловых швов применяются в соответствии с табл. 2 прил. 1 с учетом условий эксплуатации конструкций, указанных в табл. 1 прил. 1.

2.3. Расчетные сопротивления стыковых соединений , выполняемых всеми видами дуговой сварки, принимаются равными расчетным сопротивлениям стального проката при условии физического контроля качества швов в растянутых элементах и соблюдении требований п. 13.42 главы СНиП II-23-81 об обеспечении полного провара соединяемых элементов путем двухсторонней сварки, односторонней с подваркой корня шва или односторонней сварки на подкладке.

В случаях, когда в стыковых соединениях невозможно обеспечить полный провар элементов, рекомендуется принимать R_wy =0,7 R _у .

2.4. Несущая способность сварных соединений с угловыми швами зависит от ориентации шва относительно направления усилия, действующего на соединение. Однако учет этой зависимости существенно усложняет расчет соединения, в связи с чем расчетные сопротивления соед инений с угловыми швами в главе СНиП II-23-81 приняты для наименее благоприятной ориентации (флангового шва) и независимыми от величины угла между продольной осью шва и направлением силового вектора, действующего на него.

2.5. Предельным состоянием для сварных соединений с угловыми швами является опасность разрушения. В связи с этим их расчетные сопротивления установлены по временному сопротивлению металла: для металла шва - в зависимости от нормативного сопротивления металла шва R _wf = f ( R_wun ); для металла границы сплавления - в зависимости от нормативного сопротивления основного металла R _wz = f ( R_un ).

Числовые значения расчетных сопротивлений сварных соединений с угловыми швами приведены в табл. 2 и 3 прил. 1.

3. РАСЧЕТ СВАРНЫХ СОЕДИНЕНИЙ

3.1. Расчет сварных стыковых соединений на центральное растяжение и сжатие следует проводить в соответствии с п. 11.1 главы СНиП II-23-81.

3.2. С целью повышения эффективности использования наплавленного металла в соединениях с расчетными угловыми швами предусмотрено применение электродных материалов , обеспечивающих повышенные прочностные свойства металла шва. При этом возникает необходимость проверки прочности соединений по двум опасным сечениям: по металлу шва и по металлу границы сплавления.

3.3 ( 11.2). Сварные соединения с угловыми швами при действии продольной и поперечной сил следует рассчитывать на срез (условный) по двум сечениям:

по металлу границы сплавления

где l_w - расчетная длина шва, принимаемая меньше его полной длины на 10 мм; β _f и β _z - коэффициенты, принимаемые при сварке элементов из стали: с пределом текучести до 580 МПа (5900 кгс/см 2 ) по табл. 1 (34); с пределом текучести свыше 580 МПа (5900 кгс/см 2 ) независимо от вида сварки, положения шва и диаметра сварочной проволоки β _f = 0,7 и β _z = 1; γ _wf и γ _wz - коэффициенты условий работы шва, равные 1 во всех случаях, кроме конструкций, возводимых в климатических районах I ₁ , I ₂ , II ₂ и II ₃ , для которых γ _wf = 0,85 для металла шва с нормативным сопротивлением R_wun = 410 МПа (4200 кгс/см 2 ) и γ _wz = 0,85 для всех сталей.

При сварке с использованием технологических приемов, направленных на повышение производительности наплавки, которые сопровождаются снижением глубины проплавления (например, сварка при удлиненном вылете электрода, при прямой полярности постоянного тока, с применением дополнительного присадочного материала и т.п.), значения коэффициентов рекомендуется принимать β _f = 0,7 и β _z = 1.

3.4 (11.2). Для угловых швов, размеры которых установлены в соответствии с расчетом, в элементах из стали с пределом текучести до 285 МПа (2900 кгс/см 2 ) следует применять электроды или сварочную проволоку согласно табл. 2 прил. 1 настоящего пособия, для которых расчетные сопротивления срезу по металлу шва R_wf должны быть более R_wz , а при ручной сварке не менее чем в 1,1 раза превышают расчетные сопротивления срезу по металлу границы сплавления R_wz , но не превосходят значений R_wz β_z / β_f

в элементах из стали с пределом текучести свыше 285 МПа (2900 кгс/см 2 ) допускается применять электродные материалы, для которых выполняется условие

Значения коэффициентов β_f и β_z при катетах швов, мм

Автоматическая при d = 3 - 5

Автоматическая и полуавтоматическая при d = 1,4 - 2

Нижнее, горизонтальное, вертикальное

Ручная; полуавтоматическая проволокой сплошного сечения при d < 1,4 или порошковой проволокой

В лодочку нижнее, горизонтальное, вертикальное, потолочное

Примечание . Значения коэффициентов соответствуют нормальным режимам сварки.

При выборе электродных материалов следует учитывать группы конструкций и климатические районы, указанные в табл. 55 (В Пособии табл. 1 прил. 1).

3.5. Левая часть выражений (3) и (4) 1,1 R_wz < R_wf и R_wz < R_wf означает необходимость применения электродных материалов, обеспечивающих высокую прочность металла шва. Правая часть этих выражений R_wf ≤ R_wz β_z / β_f указывает верхний предел значения R_wf , выше которого увеличение прочности металла шва нецелесообразно, поскольку несущую способность соединения будет определять сечение по металлу границы сплавления.

При проектировании сварных соединений возможны исключения из требований, указанных в выражениях (3) и (4), которые определяются дискретностью значений входящих в них параметров, ограниченностью ассортимента сварочных проволок для механизированной сварки и условиями организации производства. Поэтому в ряде случаев для расчетных угловых швов целесообразно применять сварочную проволоку, при которой R_wf ≤ R_wz β_z / β_f .

3.6. В зависимости от значений R_wf _, R_wz и β_f , характеризующих соединение с угловыми швами, прочность одного из двух расчетных сечений меньше прочности другого сечения. Поэтому для расчета такого соединения на срез (условный) достаточно произвести проверку менее прочного сечения. Расчетные сечения, по которым следует производить проверку прочности соединения с угловыми швами, в зависимости от параметров R_wun _, R_un и β_f , указаны в табл. 2 (для конструкций во всех климатических районах, кроме I ₁ , I ₂ , II ₂ , II ₃ ) и табл. 3 (для конструкций в климатических районах I ₁ , I ₂ , II ₂ , II ₃ ).

Примечан ие . Коэффициенты β_f и β_z связаны зависимостью _{, поэтому в табл. 2 и 3 значения β_z не приводятся.}

3.7. Предельные усилия на сварные соединения с угло выми швами для наиболее распространенных сочетаний электродных материалов, условий сварки и катетов швов приведены в табл. 1 и 2 прил. 2.

3.8. Расчет сварных соединений с угловыми швами на действие момента, на одновременное действие сил и момента, а также поясных соединений с угловыми швами в составных двутавровых балках следует производить по двум сечениям в соответствии с требованиями п п. 11.3, 11.5 и 11.16 главы СНиП II-23-81. При этом в общем виде расчетные формулы представляют собой сравнение напряжений, возникающих от действия усилий в расчетном сечении по шву (τ _f ) и по металлу границы сплавления (τ _z ), с соответствующими расчетными сопротивлениями с учетом коэффициентов условий работы:

ПРЕДИСЛОВИЕ

Текст из главы СНиП II-23-81 отмечен в Пособии вертикальной чертой , в скобках указаны соответствующие номера пунктов и таблиц главы СНиП.

Пособие разработано ЦНИИСК им. Кучеренко (канд. техн. наук В. М . Барышев, при участии инж. Ю .А. Новикова).

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. При проектировании сварных соедине н ий следует:

предусматривать такое расположение и размеры сварных швов , при которых максимально сокращалась бы необходимость кантовки конструкций при их изготовлении, а также уменьшились бы размеры соединяемых деталей;

2. РАСЧЕТНЫЕ СОПРОТИВЛЕНИЯ СВАРНЫХ СОЕДИНЕНИЙ

2.2. Расчетные сопротивления сварных соединений, определенные по формулам, которые приведены в главе СНиП II-23-81 , обеспечиваются при соблюдении следующих условий:

В случаях, когда в стыковых соединениях невозможно обеспечить полный провар элементов, рекомендуется принимать R_wy =0,7 R _у .

2.4. Несущая способность сварных соединений с угловыми швами зависит от ориентации шва относительно направления усилия, действующего на соединение. Однако учет этой зависимости существенно усложняет расчет соединения, в связи с чем расчетные сопротивления соед и нений с угловыми швами в главе СНиП II-23-81 приняты для наименее благоприятной ориентации (флангового шва) и независимыми от величины угла между продольной осью шва и направлением силового вектора, действующего на него.

3. РАСЧЕТ СВАРНЫХ СОЕДИНЕНИЙ

3.3 ( 1 1.2). Сварные соединения с угловыми швами при действии продольной и поперечной сил следует рассчитывать на срез (условный) по двум сечениям:

N / ( β_f k_f l_w ) ≤ R_wf γ_wf γ_c ; (1) [12 0]

N / ( β_z k_f l_w ) ≤ R_wz γ_wz γ_c . (2) [121 ]

где l_w - расчетная длина шва, принимаемая меньше его полной длины на 10 мм; β _f и β _z - коэффициенты , принимаемые при сварке элементов из стали: с пределом текучести до 580 МП а (5900 кгс/см 2 ) по табл. 1 (34); с пределом текучести свыше 580 МПа (5900 кгс/см 2 ) независимо от вида сварки, положения шва и диаметра сварочной проволоки β _f = 0,7 и β _z = 1; γ _wf и γ _wz - коэффициенты условий работы шва, равные 1 во всех случаях, кроме конструкций, возводимых в климатических районах I ₁ , I ₂ , II ₂ и II ₃ , для которых γ _wf = 0 , 8 5 для металла шва с нормативным сопротивлением R_wun = 410 МПа (4200 кгс/см 2 ) и γ _wz = 0, 85 для всех сталей.

3. 4 ( 11.2). Для угловых швов, размеры которых установлены в соответствии с расчетом, в элементах из стали с пределом текучести до 285 МПа (2900 кгс/см 2 ) следует применять электроды или сварочную проволоку согласно табл. 2 прил. 1 настоящего пособия, для которых расчетные сопротивления срезу по металлу шва R_wf должны быть более R_wz , а при ручной сварке не менее чем в 1,1 раза превышают расчетные сопротивления срезу по металлу границы сплавления R_wz , но не превосходят значений R_wz β_z / β_f

в элементах из стали с пределом текучес т и свыше 285 МПа (2900 кгс/см 2 ) допускается применять электродные материалы, для которых выполняется условие

Значения коэффициентов β _f и β _z при катетах швов, мм

Автоматическая и полуавтоматическая при d = 1 , 4 - 2

Ручная; полуавтоматическая проволокой сплошного сечения при d < 1, 4 или порошковой проволокой

Примечан ие . З н ачения коэффициентов соответствуют нормальным режимам сварки.

При выборе электродных материалов следует учитывать группы конструкций и климатические районы , указанные в табл. 55 (В Пособии табл. 1 прил. 1).

3.5. Левая часть выражений (3) и (4) 1,1 R_wz < R_wf и R_wz < R_wf означает необходимость применения электродных материалов, обеспечивающих высокую прочность металла шва. Правая часть этих выражений R_wf ≤ R_wz β_z / β_f указывает верхний предел значения R_wf , выше которого увеличение прочности металла шва нецелесообразно, поскольку несущую способность соединения будет определять сечение по металлу границы сплавления.

При проектировании сварных соединений возможны исключения из требований, указанных в выражениях (3) и (4), которые определяются дискретностью значений входящих в них параметров, ограниченностью ассортимента сварочных проволок для механизирован н ой сварки и условиями организации производства. Поэтому в ряде случаев для расчетных угловых швов целесообразно применять сварочную проволоку, при которой R_wf ≤ R_wz β_z / β_f .

Примечан ие . Коэффициенты β _f и β _z связаны зависимостью , поэтому в табл. 2 и 3 значения β _z не приводятся.

3.7. Предельные усилия на сварные соединения с угло в ыми швами для наиболее распространенных сочетаний электродных материалов, условий сварки и катетов швов приведены в табл. 1 и 2 прил. 2.

3.8. Расчет сварных соединений с угловыми швами на действие момента, на одновременное действие сил и момента, а также поясных соединений с угловыми швами в составных двутавровых балках следует производить по двум сечениям в соответствии с требованиями п п . 11.3, 11.5 и 11 .1 6 главы СНиП II-23-81. При этом в общем виде расчетные формулы представляют собой сравнение напряжений, возникающих от действия усилий в расче т ном сечении по шву (τ _f ) и по металлу границы сплавления (τ _z ), с соответствую щ ими расчетными сопротивлениями с учетом коэффициентов условий работы:

расчет сварных швов на прочность

Согласно СП 16.13330.2011 "Стальные конструкции", таблица 4 получается: сварные швы "с угловыми швами", характеристика расчетного сопротивления шва - по металлу шва и по металлу границы сплавления; срез условный; Rwf = 0,55*Rwun / Ywm = 0,55*410 / 1,25 = 180,4МПа * Yc = 180,4 * 1,1 (Yс - коэффициент условия работы элементов и соединений стальных конструкций, табличные данные) =198,44 МПа - по металлу шва.

Rwz=0,45*Run = 0,45 * 360 = 162 МПа * 1,1 = 178,2 МПа - по границе сплавления металла.

Для расчета берем наименьшее значение - 178,2 МПа.

Значения коэффициентов надежности по металлу шва Ywm следует принимать:

Ywm = 1,25 - при Rwun ≤ 490 Н/мм2 (4900 кг/см2)

Ywm = 1,35 - при Rwun ≥ 590 Н/мм2 (5900 кг/см2)

Таблица 3 - коэффициенты условий работы Yс

Берем пункт 6, элементы конструкций из стали с пределом текучести до 440МПа, несущие статическую нагрузку, при расчете на прочность по сечению, ослабленному отверстиями для болтов (кроме фрикционных соединений) - Yс=1,10

Таблица 4 - расчетное сопротивление для стали

Разрушение углового сварного шва может произойти в двух плоскостях: по металлу шва, по границе сплавления, следовательно расчет угловых швов производится для этих двух сечений.

Много интересного в книге "Примеры расчета металлических конструкций" автор А.П.Мандриков, смотри ссылку.

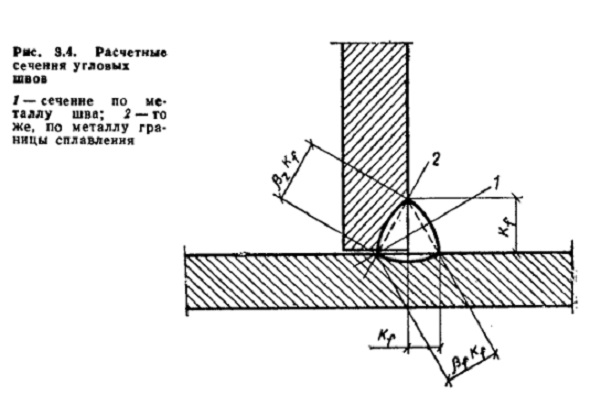
Рис 2 - сечение угловых швов, А.П. Мандриков

На рисунке показано сечение по границе сплавления, по металлу, катет шва Kf, безразмерный коэффициент Bz, Bf

Рис 3 - срез и изгиб углового шва

Тавровое сварное соединение рассматриваем как угловой шов.

При действии на угловые швы изгиба и среза, смотри рисунок 3, суммарные напряжения проверяют по формуле (Мандриков А.П.):

Gf= (τwf ^2 + Gwf ^2)^0,5 ≤ Rwf *Ywf*Yc - по металлу шва

Gz = (τwz ^2 + Gwz ^2)^0,5 ≤ Rwz *Ywz*Yc - по металлу границы сплавления

где τwf = N / (Bf*Rf) * ∑Lw;

τwz = N / (Bz*Rf) * ∑Lw;

Gwf = M / Ww = 3*N*L / (Bf*Rf) * Lw^2;

Gwz = M / Ww = 3*N*L / (Bz*Rf) * Lw^2

Катет шва Rf должен быть не менее 4мм. и не более 1,2 меньшей из толщин свариваемых элементов. Расчетная длина шва - не менее 4*Rf, но не менее 40мм.

Рассмотрим пример, согласно рисунка 3, относ составляет Lотнос = 150мм.

Нагрузка N = 500 кг. = 5000 Н.

Длина шва Lшва = Lодного шва - 2*t (толщина наименьшей из свариваемых деталей) =

= 100 - 2*6 = 88мм. Суммарная длина шва = 88 * 2 (количество швов) = 176 мм.

τwf = N / (Bf*Rf) * ∑Lw = 5000 Н / (0,7*6 мм) * 176 мм. = 6,76 Н/мм2;

τwz = N / (Bz*Rf) * ∑Lw = 5000 Н / (1,0*6 мм.) * 176 мм. = 4,73 Н/мм2;

Gwf = M / Ww = 3*N*L / (Bf*Rf) * Lw^2 = 3 * 5000 Н * 150 мм. / (0,7 * 6) * 176мм.^2 =

2250000 Н*мм. / 130099,2 мм3 = 17,29 Н*мм2;

Gwz = M / Ww = 3*N*L / (Bz*Rf) * Lw^2 = 3 * 5000 Н * 150 мм. / (1,0 * 6) * 176мм.^2 =

2250000 Н*мм. / 185856 мм3 = 12,11 Н*мм2;

Rwf *Ywf*Yc = 180,4 * 1,0 * 1,1 = 198,44 Н/мм2

Rwz *Ywz*Yc = 162 * 1,0 * 1,1 = 178,2 Н/мм2

Rwz = 0,45 * Run = 0,45 * 360 = 162 Н/мм2

Ywf и Ywz - коэффициенты работы шва, равный 1,0

Согласно СП 16.13330.2011 "Стальные конструкции" пункт 14.1.17 расчет сварных соединений с угловыми швами при действии момента М в плоскости, перпендикулярной плоскости расположения швов, следует выполнять на срез (условный) по одному из двух сечений:

по металлу шва М / (Wf*Rwf*Yc) = 750000 / 43366,4*180,4*1,1 = 0,0871 ≤ 1;

по металлу сплавления шва М / (Wz*Rwz*Yc) = 750000 / 61952*180,4*1,1 = 0,0610 ≤ 1;

Wf и Wz - моменты сопротивления расчетных сечений сварного соединения по металлу шва и по металлу границы сплавления соотвественно.

Wf = 2 * (Bf*Kf*Lw^2) / 6 = Bf*Kf*Lw^2 / 3 = 0,7*6мм.*176мм.^2 / 3 = 43366,4 мм3

Wz = 2 * (Bz*Kf*Lw^2) / 6 = Bz*Kf*Lw^2 / 3 = 1,0*6мм.*176мм.^2 / 3 = 61952 мм3

M = N * Lотнос = 5000 Н * 150мм. = 750000 Н*мм.

Определим максимальную нагрузку на 40мм. двухсторонний (по 20мм. на сторону), угловой сварной шов, катет шва 6мм. - 290кг.

Статья дана для сведения.

Что получилось в расчетной программе. Напряжение точечное - 925 МПа. В сварном шве - в зеленой зоне 123 МПа, в желтом секторе - 178 МПа, в красном секторе - 500 - 600МПа. На металле - 500 - 600 МПа. Смотри рисунок 4 и 5.

Читайте также: